ESSENTIAL NORMS OF PRODUCTS OF WEIGHTED COMPOSITION OPERATORS AND DIFFERENTIATION OPERATORS BETWEEN BANACH SPACES OF ANALYTIC FUNCTIONS∗
2015-02-10
Department of Mathematics and Statistics,College of Science,Sultan Qaboos University, P.O.Box 36,P.C.123,Al-Khod,Oman
E-mail:manhas@squ.edu.om
Ruhan ZHAO
Department of Mathematics,State University of New York Brockport,Brockport,NY 14420,USA
E-mail:rzhao@brockport.edu
ESSENTIAL NORMS OF PRODUCTS OF WEIGHTED COMPOSITION OPERATORS AND DIFFERENTIATION OPERATORS BETWEEN BANACH SPACES OF ANALYTIC FUNCTIONS∗
Jasbir Singh MANHAS
Department of Mathematics and Statistics,College of Science,Sultan Qaboos University, P.O.Box 36,P.C.123,Al-Khod,Oman
E-mail:manhas@squ.edu.om
Ruhan ZHAO
Department of Mathematics,State University of New York Brockport,Brockport,NY 14420,USA
E-mail:rzhao@brockport.edu
We obtain several estimates of the essential norms of the products of diferentiation operators and weighted composition operators between weighted Banach spaces of analytic functions with general weights.As applications,we also give estimates of the essential norms of weighted composition operators between weighted Banach space of analytic functions and Bloch-type spaces.
diferentiation operators;weighted composition operators;weighted Banach space of analytic functions;Bloch-type spaces;essential norms
2010 MR Subject Classifcation47B38;47B33
1 Introduction
Let D be the unit disk in the complex plane C,and let H(D)denote the space of analytic functions on D.Let φ be an analytic self-map on D and let ψ∈H(D).The weighted composition operator Wψ,φon H(D)is defned as follows
Weighted composition operators appear in a natural way on diferent settings.For example, it is well-known that isometries on most of the spaces of analytic functions are described as weighted composition operators.For details on isometries on function spaces,we refer to the monographs of Fleming and Jamison([6],[7]).In recent years many authors have started exploring the operator theoretic properties of Wψ,φon various spaces of analytic functions such as the Bloch space,the Bergman spaces,the Hardy spaces and the weighted Banach spaces of analytic functions in terms of the function-theoretic properties of the symbols ψ and φ.The theory of weighted composition operators unifes the theory of multiplication operators and composition operators.For the information on composition and weighted composition operators see,for example,books[5],[18]and[19].
The diferentiation operator D which is defned by Df=f′is typically unbounded on many analytic function spaces.The product of weighted composition operators and diferentiation operators,denoted by DWψ,φand Wψ,φD,respectively,are defned as
for every f∈H(D).
For ψ(z)=1,the operators DCφ=Wφ′,φD and CφD were frst studied by Hibschweiler and Portnoy in[10]and then by Ohno in[16],where boundedness and compactness of DCφbetween Hardy spaces and Bergman spaces were investigated.Later on these operators have been studied by many authors.
For the operators DWψ,φ,in a series of papers,[20],[21],[22]and[23],Stevi´c studied these operators from various spaces into weighted Banach spaces(called weighted-type spaces in these papers)or nth weighted Banach spaces,either on the unit disk or on the unit ball. In a recent paper[14],the authors obtained characterizations of boundedness and compactness of the operator DWψ,φand Wψ,φD between weighted Banach spaces of analytic functions on D with general weights.In this paper we continue this line of research,and obtain estimates of the essential norms of such operators.Recall that the essential norm‖T‖eof a bounded operator T between Banach spaces X and Y is defned as the distance from T to the space of compact operators from X to Y.Hence T is compact if and only if‖T‖e=0.
In Section 2,we introduce some concepts that are needed later.We give estimates of the essential norms in terms of Schwarz-Pick type quotients in Section 3;and estimates of the essential norms in terms of n-th power of φ in Section 4.
2 Preliminaries
Let v be a strictly positive,continuous and bounded function on D.We will call such a function v as a weight function or simply a weight.We defne the general weighted Banach space of analytic functions as follows:
We also defne
For a given weight v its associated weight~v is defned as follows:


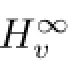

for every z∈D.The following condition(L1)introduced by Lusky in[12]is important for our research.
Radial weights which satisfy(L1)are always essential(see[4]).We note here that the standard weights vα(z)=(1-|z|2)α,where α>0,and the logarithmic weight vβ(z)=(1-log(1-|z|2))β, where β<0,satisfy condition(L1).We refer to[2],[3],[11]and[12]for more details of the weighted Banach spaces of analytic functions.
The Bloch-type space Bvis defned as follows:

In the following,the notation A≈B means there is a positive constant C such that C-1B≤A≤CB,
3 Essential Norms
In order to prove our result,we need the following result.

for every z∈D.
We note here that,since v satisfes condition(L1),it is essential,and so equation(2.1) holds.Therefore,if we let C~v=kCv,where k is the constant in(2.1),then from equation(3.1)
we obtain
We also need the following lemma.which is essentially given by Montes-Rodr´ıguez in[15].

(i)Each Lnis compact.

ProofThe proof of(i),(ii)and(iv)are the same as in[15].(iii)can be obtained from (ii)by using Cauchy’s formula.We omit the details here.?
Let
The following is our main result.

where C~vis the constant in(3.2)(which only depends on the weight function v).
ProofThe lower estimate.Let{zn}⊂D be a sequence with|φ(zn)|→1 as n→∞, such that

if v is satisfes condition(L1).Let
and defne

4.4 从各地不同等级年平均降水日数而言,除≥1.0mm的降水日数有所下降外,其他不同等级降水日数均呈增加趋势,增加幅度较小,平均每10a增加0.3~0.5d。
Hence
Taking the infmum on both sides over all compact operators K we obtain
This means that
Now we deal with the term B.Let{gn}be the same sequence given above.By(3.2)we know that
for every z∈D.Hence
Thus
Therefore
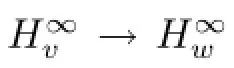
By Triangle inequality,and using(3.3),we obtain
Now let Lnbe the operator given in Lemma 3.2.Then
Fix any 0<t<1.We write I1as
Hence,applying(3.3)and Lemma 3.2 we obtain
as n→∞.For J2we have
Similarly,we write I2as
Hence,applying(3.4)and Lemma 3.2 we obtain
as n→∞.For K2we have
where C~vis the constant in(3.2).Combining the above inequalities we obtain
Letting n→∞on both sides we get
for every s∈(0,1).Thus
The proof is complete.

Corollary 3.2Let v be a radial weight satisfying condition(L1),and let w be an arbitrary weight.Let Wψ,φbe a bounded operator from to Bw.Then
where C~vis the constant in(3.2)(which only depends on the weight function v).
Let
Similarly to the proof of Theorem 3.1 we obtain the following result for the operator Wψ,φD, and we omit the proof.
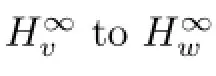
Using isometries D and T we immediately obtain

4 Essential Norms in Terms of φn
Recently,Wulan,Zheng and Zhu obtained the following result in[25].
Theorem ALet φ be an analytic self-map of D.Then Cφis compact on the Bloch space B if and only if
The result has been generalized in several papers,in which characterizations of boundedness,compactness and estimates of essential norms of composition and weighted composition operators between Bloch type spaces were obtained.See,for example,[8],[9],[13]and[27]. Here we also give the essential norm estimates for the products of weighted composition operators and diferentiation operators between Banach spaces of analytic functions in terms of φn. We need the following result,due to Montes-Rodr´ıguez(Theorem 2.1 in[15])and Hyv¨arinen, et.al.(Theorem 2.4 in[8]).

Our result will be better stated using the following two integral operators.Let ψ be an analytic function on D.For every f∈H(D),defne
The operators Jψ,sometimes referred as Ces`aro type operators or Riemann-Stieltjes integral operators,were frst used by Ch.Pommerenke in[17]to characterize BMOA functions.They were frst systematically studied by A.Aleman and A.G.Siskakis in[1].They proved that Jψis bounded on the Hardy space Hpif and only if ψ∈BMOA.Thereafter many authorsstudied these operators.The operators Iψ,as companions of Jψ,have been also studied,see, for example,[26].


ProofBy Theorem B,
Hence the result follows from Theorem 3.1.
From(3.5)we immediately obtain

Similarly,by Theorem 3.3 and Theorem B,we immediately obtain the following result.

Again,using isometries D and T we immediately obtain

AcknowledgementsThe second author would like to thank Sultan Qaboos University for the support and hospitality.
[1]Aleman A,Siskakis A G.An integral operator on Hp.Complex Variables,1995,28:149-158
[2]Bierstedt K D,Bonet J,Galbis A.Weighted spaces of holomorphic functions on balanced domains.Michigan Math J,1993,40:271-297
[3]Bierstedt K D,Bonet J,Taskinen J.Associated weights and spaces of holomorphic functions.Studia Math, 1998,127:70-79
[4]Bonet J,Domanski P,Lindstr¨om M,Taskinen J.Composition operators between weighted Banach spaces of analytic functions.J Austral Math Soc(Ser A),1998,64:101-118
[5]Cowen C,MacCluer B.Composition Operators on Spaces of Analytic Functions.Boca Raton:CRC Press, 1995
[6]Fleming R J,Jamison J E.Isometries on Banach Spaces:Function Spaces.Chapman and Hall,2002
[7]Fleming R J,Jamison J E.Isometries on Banach Spaces:Vector-Valued Function Spaces,Vol 2.Chapman and Hall/CRC,2008
[8]Hyv¨arinen O,Kemppainen M,Lindstr¨om M,Rautio A,Saukko E.The essential norm of weighted composition operators on weighted Banach spaces of analytic functions.Integr Equ Oper Theory,2012,72: 151-157
[9]Hyv¨arinen O,Lindstr¨om M.Estimates of essential norms of weighted composition operators between Blochtype spaces.J Math Anal Appl,2012,393:38-44
[10]Hibschweiler R A,Portnoy N.Composition followed by diferentiation between Bergman and Hardy spaces. Rocky Mountain J Math,2005,35:843-855
[11]Lusky W.On the structure of Hv0(D)and hv0(D).Math Nachr,2002,159:279-289
[12]Lusky W.On weighted spaces of harmonic and holomorphic functions.J London Math Soc,1995,51: 309-320
[13]Manhas J S,Zhao R.New estimates of essential norms of weighted composition operators between Bloch type spaces.J Math Anal Appl,2012,389:32-47
[14]Manhas J S,Zhao R.Products of weighted composition operators and diferentiation operators between Banach spaces of analytic functions.Acta Sci Math(Szeged),to appear
[15]Montes-Rodr´ıguez A.Weighted composition operators on weighted Banach spaces of analytic functions.J London Math Soc,2000,61(2):872-884
[16]Ohno S.Products of composition and diferentiation between Hardy spaces.Bull Austral Math Soc,2006, 73:235-243
[17]Pommerenke Ch.Schlichte Funktionen und analytische Funktionen von beschr¨ankten mittlerer Oszillation. Comm Math Helv,1977,52:591-602
[18]Shapiro J H.Composition Operators and Classical Function Theory.New York:Springer-Verlag,1993
[19]Singh R K,Manhas J S.Composition Operators on Function Spaces.North-Holland Math Studies 179. Amsterdam,New York:Elsevier Science Publications,1993
[20]Stevi´c S.Weighted diferentiation composition operators from mixed-norm spaces to weighted-type spaces. Appl Math Comput,2009,211:222-233
[21]Stevi´c S.Weighted diferentiation composition operators from H∞and Bloch spaces to nth weighted-type spaces on the unit disk.Appl Math Comput,2010,216:3634-3641
[22]Stevi´c S.Weighted diferentiation composition operators from the mixed-norm space to the nth weightedtype space on the unit disk.Abstr Appl Anal,2010,Art ID 246287
[23]Stevi´c S.Weighted iterated radial composition operators between some spaces of holomorphic functions on the unit ball.Abstr Appl Anal,2010,Art ID 801264
[24]Wolf E.Composition followed by diferentiation between weighted Banach spaces of holomorphic functions. RACSAM,2011,105:315-322
[25]Wulan H,Zheng D,Zhu K.Composition operators on BMOA and the Bloch space.Proc Amer Math Soc, 2009,137:3861-3868
[26]Yoneda R.Pointwise multipliers from BMOAαto BMOAβ.Complex Variables,2004,19:1045-1061
[27]Zhao R.Essential norms of composition operators between Bloch type spaces.Proc Amer Math Soc,2010, 138:2537-2546
[28]Zhu K.Operator Theory in Function Spaces.New York:Marcel Dekker,1990
∗Received August 6,2014.The research was supported by SQU Grant No.IG/SCI/DOMS/11/01.
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY FOR A GENERALIZED JEFFREY’S INTEGRAL MODEL FOR VISCOELASTIC FLUIDS∗
- ON A CHARACTERIZATION OF THE S-ESSENTIAL SPECTRA OF THE SUM AND THE PRODUCT OF TWO OPERATORS AND APPLICATION TO A TRANSPORT OPERATOR∗
- CONSENSUS ANALYSIS AND DESIGN OF LINEARINTERCONNECTED MULTI-AGENT SYSTEMS∗
- ITERATIVE REGULARIZATION METHODS FOR NONLINEAR ILL-POSED OPERATOR EQUATIONS WITH M-ACCRETIVE MAPPINGS IN BANACH SPACES∗
- ASYMPTOTIC STABILITY OF TRAVELING WAVES FOR A DISSIPATIVE NONLINEAR EVOLUTION SYSTEM∗
- A MODIFIED TIKHONOV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OF LAPLACE EQUATION∗
