重力异常分离的小波域优化位变滤波方法

刘彩云， 姚长利， 郑元满

1 长江大学 信息与数学学院， 湖北荆州 4340232 中国地质大学 地球物理与信息技术学院， 北京 100083



重力异常分离的小波域优化位变滤波方法

刘彩云1, 2， 姚长利2*， 郑元满2

1 长江大学 信息与数学学院， 湖北荆州 4340232 中国地质大学 地球物理与信息技术学院， 北京 100083

在重力异常分离中，频率域滤波分离方法是以全局数据频谱特征设计针对性的滤波器实现的.滤波器参数与空间位置无关，因此无法针对局部数据频谱特征动态调整滤波器参数.针对该局限性，在小波域滤波理论和优化滤波方法的基础上，本文研究提出了小波域优化位变滤波法，该方法具有空间变化滤波能力，在不同空间位置实现不同的滤波器特性，从而能实现局部数据频谱与全局数据频谱存在较大差异的重力异常分离问题.理论模型数据分离实验结果表明，在局部数据频谱与全局数据频谱差异较大的情况下，该方法相对于Butterworth滤波和优化滤波等方法具有优势.最后，用一个实例进行检验计算，体现了所提方法技术的效果和应用前景.

异常分离； 小波域； 优化滤波； 位变滤波； 重力异常

1 引言

实测重力异常是不同埋深、不同规模、不同形态的所有密度不均匀地质体重力效应的叠加，若要由实测重力异常反演某个特定地质体，必须先从叠加的重力异常中分离出单纯由该目标地质体引起的异常，再用分离出的异常进行反演和解释.由于重力场具有固有的多解性，从叠加异常中分离出目标地质体的单一异常是困难的.重力异常的有效分离是目前重力资料处理解释中的难题之一.

重力异常分离的方法很多，现在常用的主要包括最小二乘平滑法、解析延拓法、趋势分析法、匹配滤波法、补偿圆滑滤波法、正则化滤波法、维纳滤波法、小波变换法、非线性滤波法、优化滤波法等（Spector and Grant, 1970; 侯重初, 1981; 安玉林和管志宁, 1985; Gupta and Ramani, 1980; Pawlowski and Hansen, 1990; Pawlowski, 1994; Fedi and Quarta, 1998; Ridsdill-Smith, 1998; 杨文采等, 2001; Keating and Pinet, 2011; 郭良辉等2012）.这些方法具有各自的特点与优势，但同时也存在各自的局限性.

例如，维纳滤波法中，为了准确地分离出目标地质体引起的异常，需要先估计出目标地质体的频谱，再以此为依据设计维纳滤波器.针对这个问题，Gupta和Ramani（1980）采用径向谱分析方法，估计目标地质体的频谱；Pawlowski和Hansen（1990）利用钻孔数据等先验地质信息构建模型，估计目标地质体的频谱，此后，Pawlowski（1994）又提出利用格林等效层理论估计目标地质体频谱的方法；郭良辉等（2012）在优选延拓的理论基础上，进一步研究提出基于维纳滤波和格林等效层理论的优化滤波法，该方法分离重力异常不需要已知延拓高度，可对重力异常进行指定频段的低通带通和高通滤波.这些经典的频率域分离方法都是根据全局数据频谱特征设计滤波器进行滤波分离，对于局部数据频谱和全局数据频谱差异较大的重力异常分离，频率域分离方法的效果有待改进.熊光楚（1979）、熊光楚和张福荣（1981）曾针对线性滤波器局限性问题，研究并提出用于重磁异常解释的空间域位变滤波器.只是当时考虑的还是异常组合不太复杂的简单情况，还不适合大数据量及复杂异常的分离情况.

小波变换是近年来获得广泛应用的一种数字信号处理工具，小波变换也可用于估计信号的局部频谱特性.Kaiser（1996）经过理论推导指出，对信号进行频率域滤波操作，可通过对信号的小波变换系数进行线性组合运算来近似实现，并称之为小波域滤波.本文针对常规频率域滤波方法存在的不具有位变滤波的局限性问题，在小波域滤波理论和优化滤波方法的基础上，研究提出小波域优化位变滤波方法，该方法充分发挥小波变换的空间定位优点，能在不同空间位置表现出不同的滤波器特性，适用于局部数据频谱与全局数据频谱存在较大差异的重力异常分离问题.

本文首先简要阐述小波域滤波方法，然后给出小波域位变滤波器设计方法和小波域优化位变滤波方法及其计算步骤，再利用该方法对理论模型数据进行异常分离实验，并与Butterworth滤波（李钟慎, 2006）和频率域优化滤波法（郭良辉等, 2012）的处理结果进行对比，最后，用一个实例检验了所提方法技术的效果.

2 小波域优化位变滤波

2.1 小波域滤波原理

小波域滤波是基于小波变换的滤波方法，Kaiser（1996）给出了详细的理论推导，这里先做简要阐述.

信号s（x）的连续小波变换（ContinuousWaveletTransform,CWT）定义为：

（1）

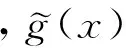
令

（2）

公式（1）可用卷积方式描述如下：

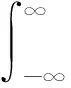
（3）

对公式（3）两边做傅里叶变换，可得：

（4）

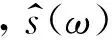
为便于后面的描述，简记为：

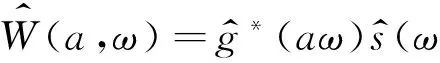
（5）

为实现滤波功能，将公式（5）两边同乘以向量v，v=（v1,v2,…,vk），其第i个分量vi是第i个尺度ai的函数vi=v（ai）（i=1,2,…,k），vi称为滤波器的等效系数.可得：

（6）

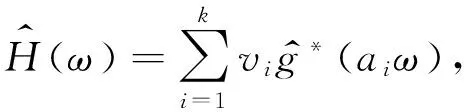
（7）

则（6）式简写为

（8）

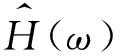
对公式（8）两边做傅里叶反变换，可得到：

（9）

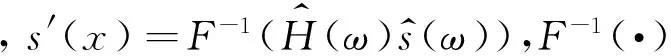
公式（9）表示，信号s′（x）可按如下步骤得到：先对原信号s（x）做小波变换，然后对小波变换系数W（ai,b）加权求和，权重系数即为小波域滤波器等效系数vi.

2.2 小波域位变滤波

本文将Kaiser（1996）给出的小波域滤波器的构建方法进行推广，构建小波域位变滤波器.具体构建过程如下：

假设公式（6）中滤波器等效系数vi不仅与尺度ai有关，而且与空间位置b有关，即为函数v（ai,b）.则公式（6）可写作：

（10）

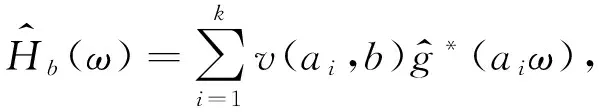
（11）

公式（10）简写为：

（12）

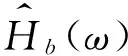
对公式（12）两边做傅里叶反变换，可得到：

（13）

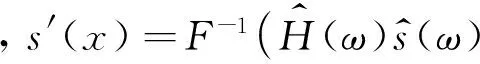
将公式（11）展开，写成如下的方程组形式：

（14）

值得指出的是，求解方程组（14）得到的v（ai,b）是该方程组的最小二乘解，因此，不可避免的会引入误差，为后面叙述方便，本文称之为小波域位变滤波误差.

小波域位变滤波仿真实验结果见3.1节.

2.3 小波域优化位变滤波

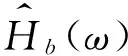
基于小波变换进行优化位变滤波计算的主要步骤如下：

（1） 根据实测异常数据的区域特征和数据处理的需要，将实测异常数据进行分块（对数据做小波变换时频分析，确定各频率成分在空间的分布规律），相邻分块在边界处可相互重叠或不重叠，本文选择相邻分块间不重叠.

（2） 对每块实测数据进行频率域优化滤波法的特征评价，设计从第j块异常数据中分离出第l层数据的优化滤波转换函数Hjl（r）.

i） 进行傅里叶变换，计算第j块异常数据的对数功率谱Pj（r）.

ii） 分段线性拟合第j块异常数据的对数功率谱.

分析第j块异常数据的对数功率谱，确定频段数和各频段的频率范围，每一频段对应一个格林等效层.利用直线Pjl（r）=Kjlr+Bjl拟合每一频段异常数据对数功率谱，其中，Kjl,Bjl分别是拟合第j块异常数据的第l频段的直线的斜率和截距.

iii） 用格林等效层对数功率谱拟合第j块异常数据实测对数功率谱Pj（r）.

iv） 假设目标层与其他深度层场源信息互不相关，则可设计从第j块异常数据中分离出第l层数据的优化滤波转换函数.具体为

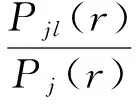
（15）

其中，Pj（r）是第j块异常数据的功率谱密度函数，Pjl（r）是第j块异常数据第l层（目标层）异常数据的功率谱密度函数.

（4） 将每个分块异常数据计算得到的局部滤波等效系数向量v（bj）根据其空间位置进行组合，得到全体重力异常的小波域位变滤波等效系数向量v（b）.

（5） 对全体重力异常数据做小波变换，得到小波变换系数W（a,b）.

（6） 将小波域位变滤波器等效系数向量v（b）和W（a,b）代入公式（13），计算得到小波域优化位变滤波分离出的目标层（第l层）异常数据.

（7） 算法结束.

基于此，我们就建立了小波域优化位变滤波方法.下面通过理论数据分离实验和实测资料处理，测试其效果.

3 理论数据分离实验

3.1 小波域位变滤波实验

实验1：小波域位变滤波器的特点是滤波器参数可随空间位置的变化而变化，下面以一维信号为例，说明小波域位变滤波的功能.给定如下信号：

（16）其中，f1=0.005 cycles·m-1，f2=0.01 cycles·m-1，f3=0.04 cycles·m-1，f4=0.08 cycles·m-1.实验1信号波形及其小波变换时频分析如图1所示.

从图1a可看出，该信号含有四个不同的频率成分，且具有明显的位置特征（x≤500 m处是频率为0.005 cycles·m-1和0.01 cycles·m-1的信号，x>500 m处是频率为0.04 cycles·m-1和0.08 cycles·m-1的信号）.从图1b所示的小波变换时频分析图（为无量纲的小波系数）可以看出，以x=500 m处为界，时频分析图的左右两半部分具有明显不同的频率成分.其中，x≤500 m处具有两段大尺度的能量异常，表明x≤500 m区域有两个低频信号；x>500 m处具有两段小尺度的能量异常，表明x>500 m处有两个高频信号.

对实验1信号分别采用传统的频率域滤波和小波域位变滤波方法进行对比实验，结果如图2—4所示.其中，采用截止频率为0.008 cycles·m-1，阶数为16的Butterworth（李钟慎，2006）低通/高通滤波器，滤波结果如图2所示.

采用截止频率为0.06 cycles·m-1，阶数为16的Butterworth低通/高通滤波器，滤波结果如图3所示.

采用小波域位变滤波器，该滤波器在x≤500 m的地方截止频率为0.008 cycles·m-1，在x>500 m的地方截止频率为0.06 cycles·m-1，小波域位变滤波器滤波结果如图4所示.

从图2—4可以看出：

（1） 采用频率域滤波分离时，若设截止频率为0.008 cycles·m-1，则能分离出x≤500 m处的两个信号：频率分别为0.005 cycles·m-1和0.01 cycles·m-1，但无法分离x>500 m处的两个信号：频率分别为0.04 cycles·m-1和0.08 cycles·m-1（见图2）；

（2） 若设截止频率为0.06 cycles·m-1，则能分离出x>500 m处的两个信号：频率分别为0.04 cycles·m-1和0.08 cycles·m-1，但无法分离x≤500 m处的两个信号：频率分别为0.005 cycles·m-1和0.01 cycles·m-1（见图3）；

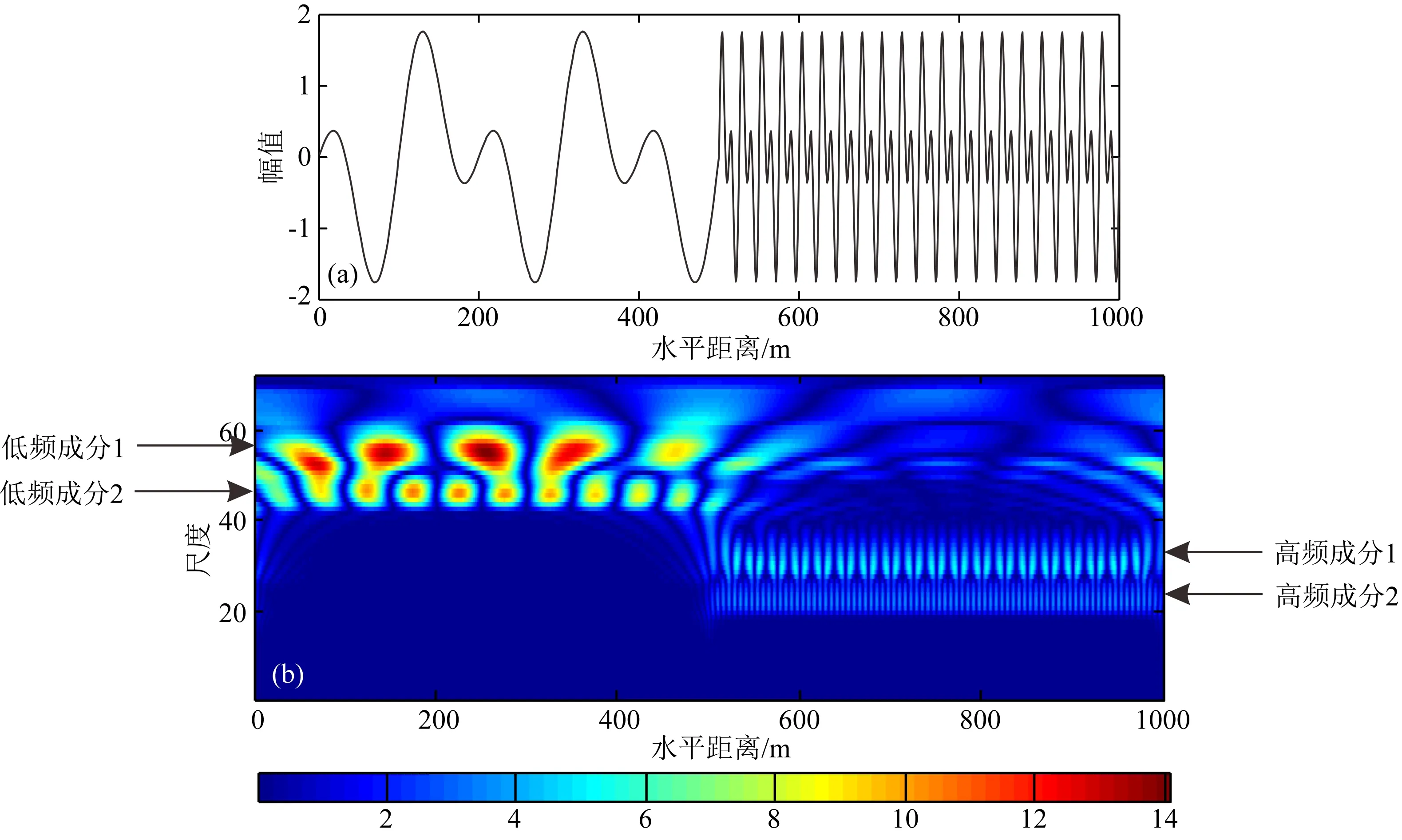
图1 实验1信号及其小波变换时频分析图

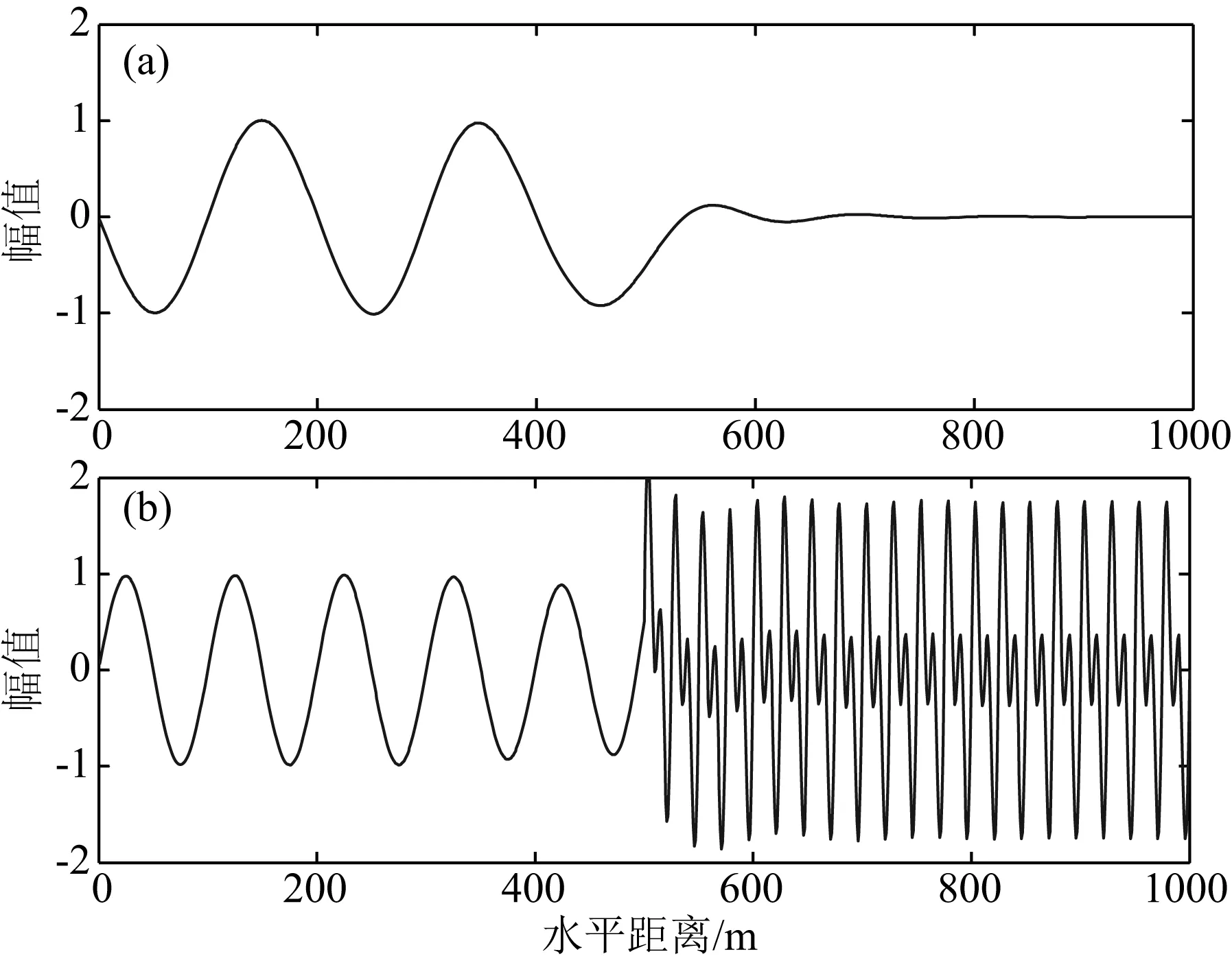
图2 截止频率0.008 cycles·m-1的Butterworth低通/高通滤波结果

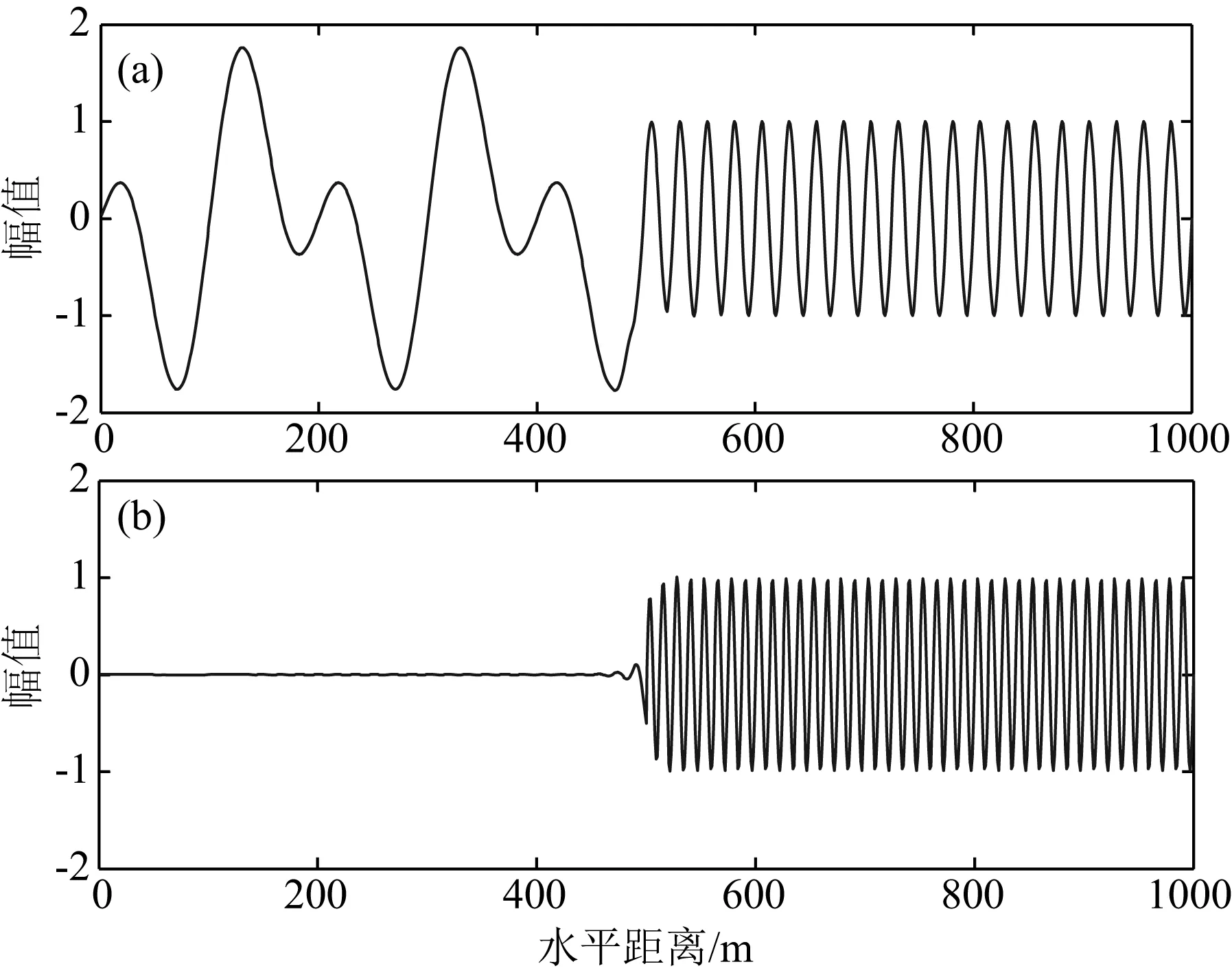
图3 截止频率0.06 cycles·m-1的Butterworth低通/高通滤波结果

（3） 采用小波域位变滤波分离时，设x≤500 m处截止频率为0.008 cycles·m-1，x>500 m处截止频率为0.06 cycles·m-1，能同时分离出四个频率的信号（见图4）.

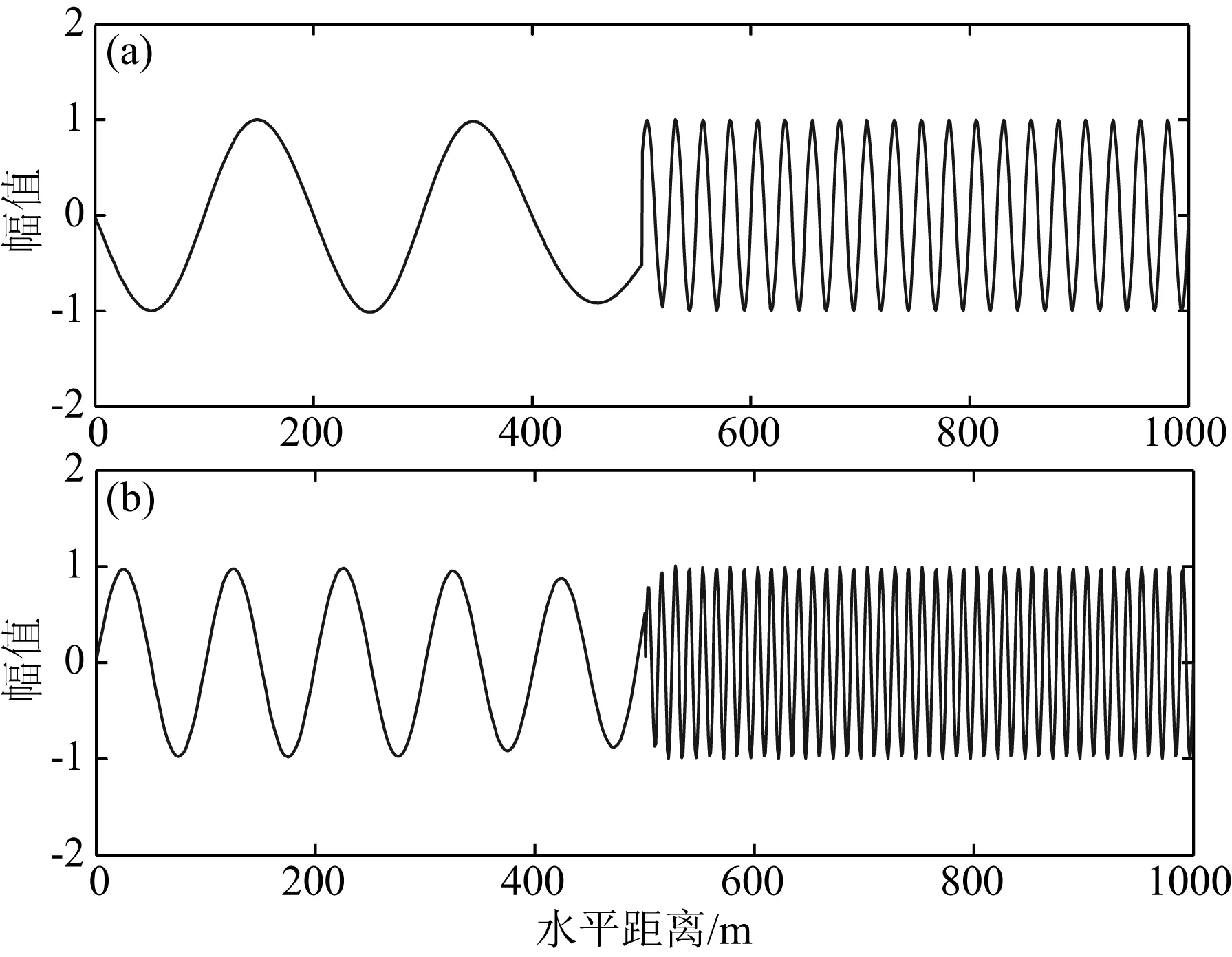
图4 小波域位变滤波结果（x≤500 m处截止频率0.008 cycles·m-1，x>500 m处截止频率0.06 cycles·m-1）

小波变换这种能根据信号不同位置的特点，设计针对性的适应位置变化的位变滤波功能，显然是过去传统的重磁处理滤波方法手段所不具有的.经典的频率域滤波实现重磁异常分离方法是根据全局数据的频谱特征设计滤波器进行滤波分离的，当局部数据频谱与全局数据频谱差异较大时，频率域分离方法会遇到和图2、图3类似的困难，难以进行精细定位分离.小波域位变滤波方法能针对不同局部数据采用不同滤波器，能有效克服分离不精细的缺陷.

3.2 理论模型数据实验

实验2：为了检验小波域优化位变滤波的效果，我们设计了如下组合模型，该组合模型由四个水平无限延伸的长方体构成，各模型参数如表1所示.在地表测点间距20 m，剖面长度为10000 m，重力异常及模型分布剖面如图5所示.

图5为组合模型的重力异常.从异常分布可以看出，尽管模型1、2的异常幅值比模型3、4的异常要小，但其异常宽度要更窄，如果简单地基于频谱分析进行常规谱分离，则只能将异常体1、2的异常分离出来，而无法分离出相对较浅的异常体1、3的异常，而这方面正是小波域优化位变滤波能体现的特点.

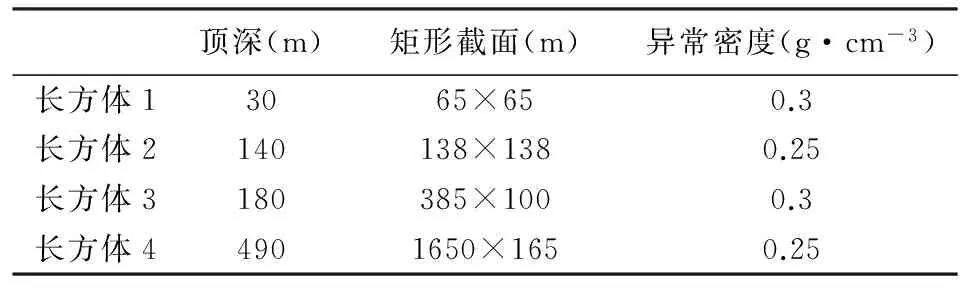
表1 实验2各模型参数表

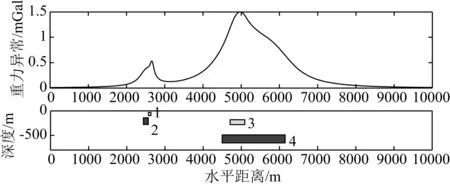
图5 实验2重力异常及其剖面图

下面分别采用频率域优化滤波和小波域优化位变滤波方法进行重力异常分离对比实验.功率谱分段拟合分析对频率域优化滤波分离效果起到重要作用，功率谱分段拟合分得越细，优化滤波分离结果越好.为了客观对比频率域优化滤波方法和小波域优化位变滤波方法，我们在两种方法中均采用低频、中频、高频三个频段分段拟合，分别对应区域异常、局部异常和拟合误差（其含义后面阐述）.模型实验2重力异常功率谱分析如图6所示.

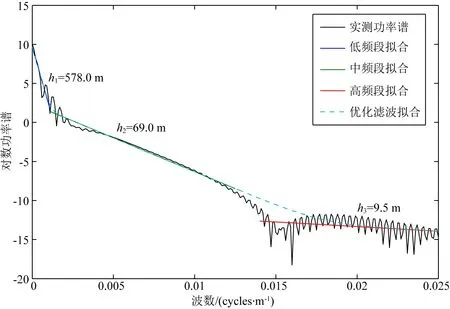
图6 频率域优化滤波法功率谱分析与拟合结果

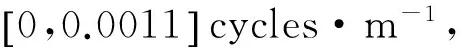
以此为指导，设计频率域优化滤波器，模型实验2的频率域优化滤波法分离结果如图7所示.其中，低通滤波分离结果为深部区域异常，带通滤波分离结果为浅部局部异常，高通滤波分离结果为优化滤波中采用格林等效层近似实测数据所产生的拟合误差（郭良辉等, 2012）.

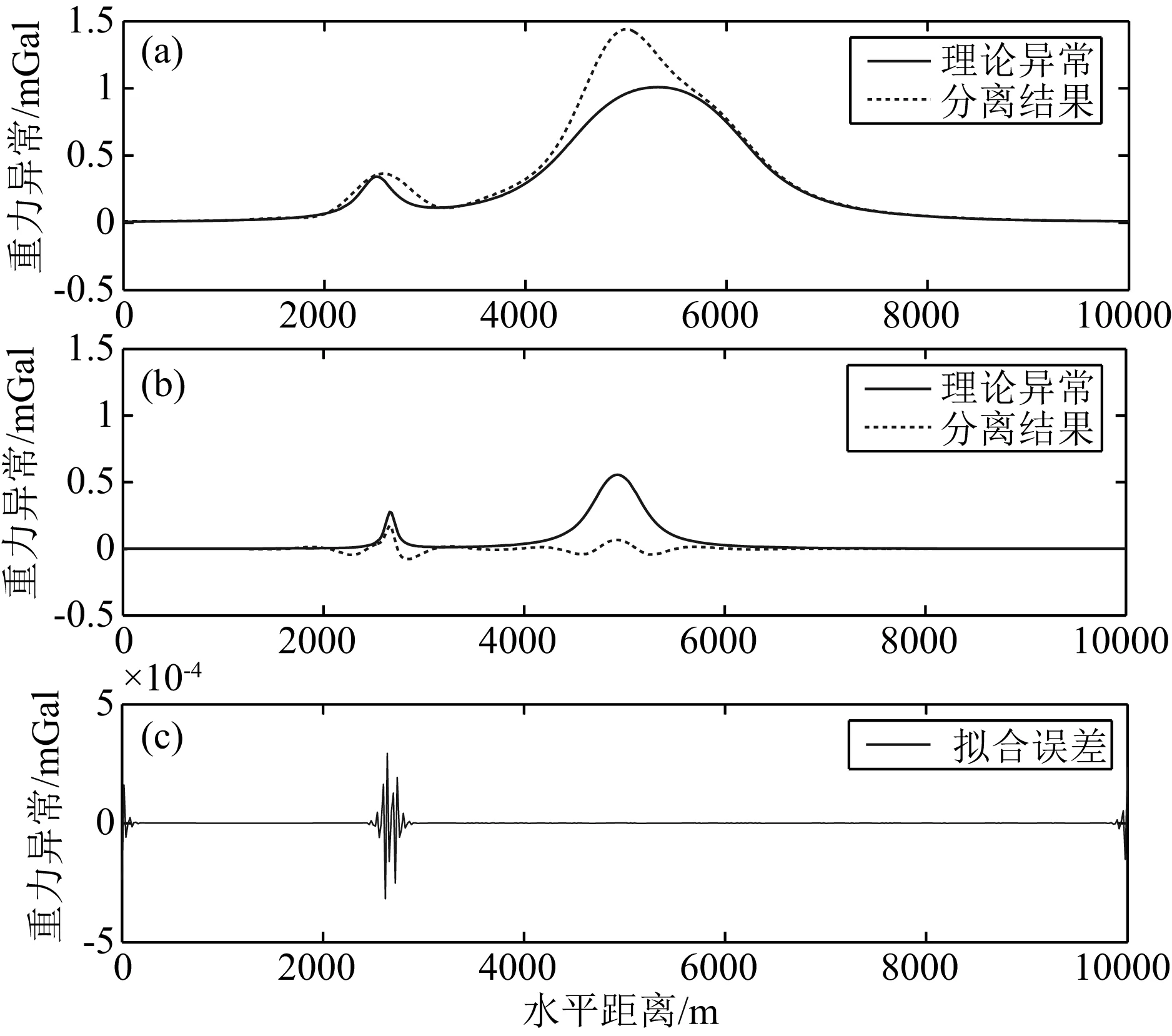
图7 实验2重力异常频率域优化滤波分离结果

从图7可以看出，分离出的区域异常（图7a）主要是长方体2、3、4的异常，同时含有少量的长方体1的异常；分离出的局部异常（图7b）主要是长方体1的异常，同时含有极少量的长方体3的异常.值得注意的是，在区域异常中（图7a），长方体3、4的异常叠加在一起，未能有效分离开.如果单从深浅场源分离的角度看（即将浅部场源1、3从相对较深的场源2、4中分离出来），这个效果也不好，同时也不可能效果好.因为比较而言，局部深的场源2（相对于场源1）与局部浅的场源3（相对于场源4）相比，场源2的频谱反而更高，常规的整体频谱分离方式，不可能将场源2归算为深部场源，以及将场源3归算为浅部场源.小波位变滤波则具有这样的能力.

对模型实验2的重力异常数据进行小波变换时频分析，如图8所示.这里需要说明的是，图8中的大尺度对应于低频异常成分，反映的是深部场源信息，为了尺度与深度直观对应，图8中纵坐标选择从大到小.

从图8可以看出，大致以x=3500 m为界，图的左右部分具有不同的频率成分，其中，x>3500 m处具有明显强的低频成分和中频成分，而x<3500 m处，低频成分强度较小，且具有频率更高的高频成分（小波系数延伸到更小尺度处）.以此为依据，将实验1的模型重力异常以x=3500 m为界分为前后两段局部数据，分别对局部数据进行功率谱分析（如图9所示），两段局部数据的功率谱与全局数据的功率谱存在明显的差异.如果能根据每段局部数据的功率谱特征，有针对性的设计适用于该段局部数据的滤波器，则有望改善分离效果.

分别对分段后的局部数据进行功率谱分析和分段线性拟合，结果如图10所示.

以图10结果为依据，按照本文2.3节所述的方法设计小波域优化位变滤波器，模型重力异常分离结果如图11所示.其中，位变低通、带通滤波分离结果为深部区域异常和浅部局部异常，位变高通滤波分离结果为拟合误差，由优化滤波拟合误差（郭良辉等, 2012）、小波域位变滤波误差和分块频谱估计所引入误差的叠加而成.

从图11所示的小波优化位变滤波分离结果可以看出，仅需采用一次小波域位变滤波，即可有效分离出四个长方体的异常.其中，分离出的区域异常包含长方体2、4的异常，局部异常包含长方体1、3的异常，与给定的模型符合性明显改进.

值得指出的是，图7c中优化滤波高通滤波结果优于图11c中小波优化位变滤波高通滤波结果，这是因为图11c中除了含有与图7c相同的优化滤波拟合误差（郭良辉等, 2012）之外，还含有小波域位变滤波误差和分块频谱估计引入的误差.小波域优化位变滤波中，高通滤波结果的幅值明显小于低通和带通滤波结果的幅值，若我们重点关注区域异常/局部异常分离效果的改善，则该方法对拟合误差的小幅放大或可接受.另外，小波域优化位变滤波的拟合误差与选用的母小波有关，可以通过选用最佳的母小波等方法减小拟合误差，由于篇幅限制，将另文详细描述.

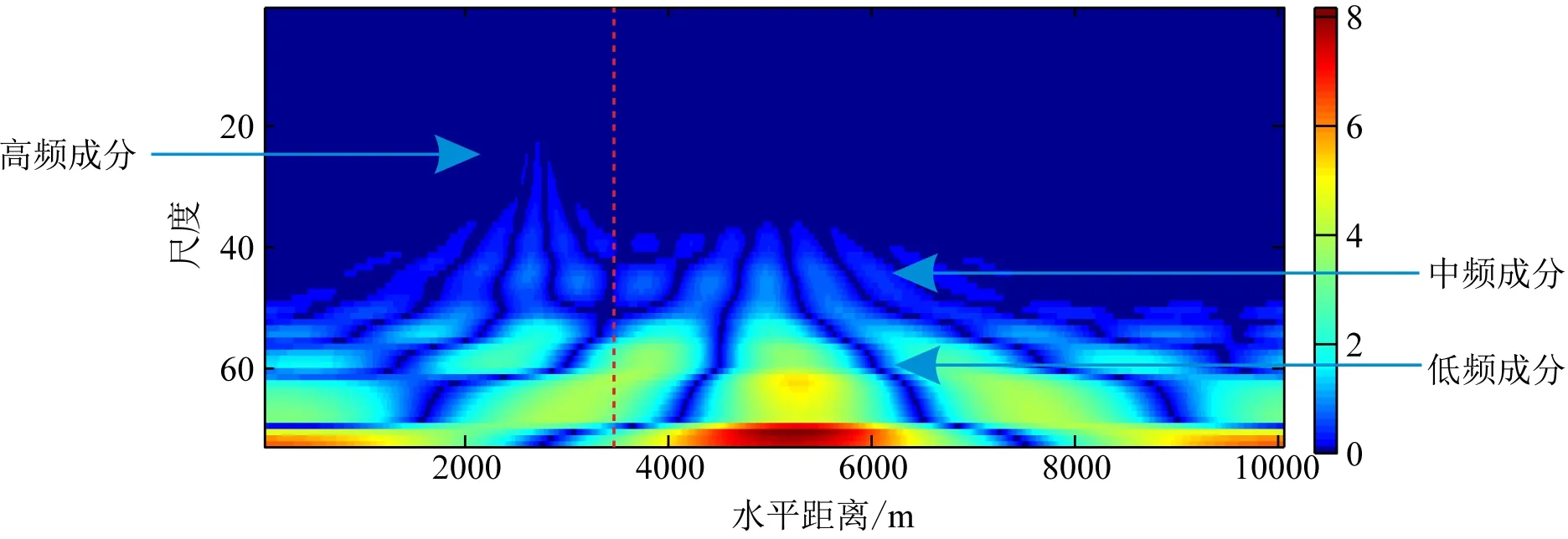
图8 实验2重力异常数据小波时频分析图

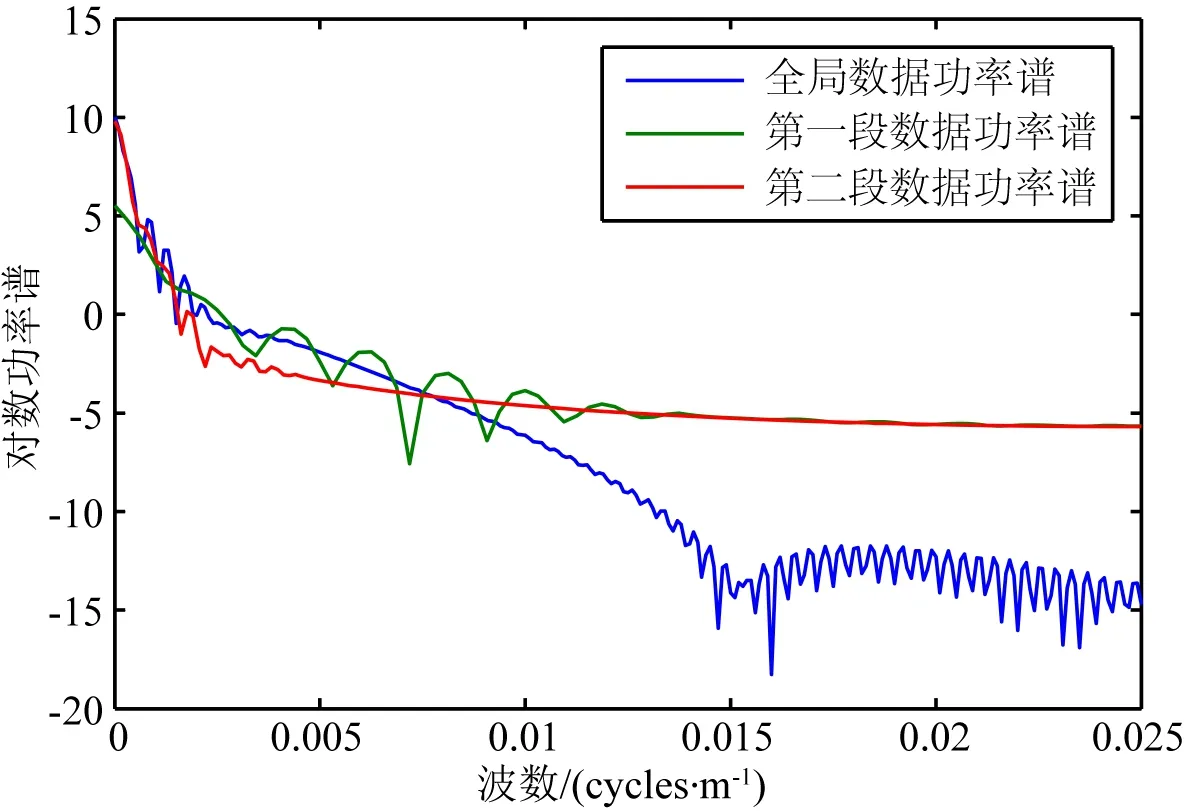
图9 全局数据与局部数据功率谱分析对比图

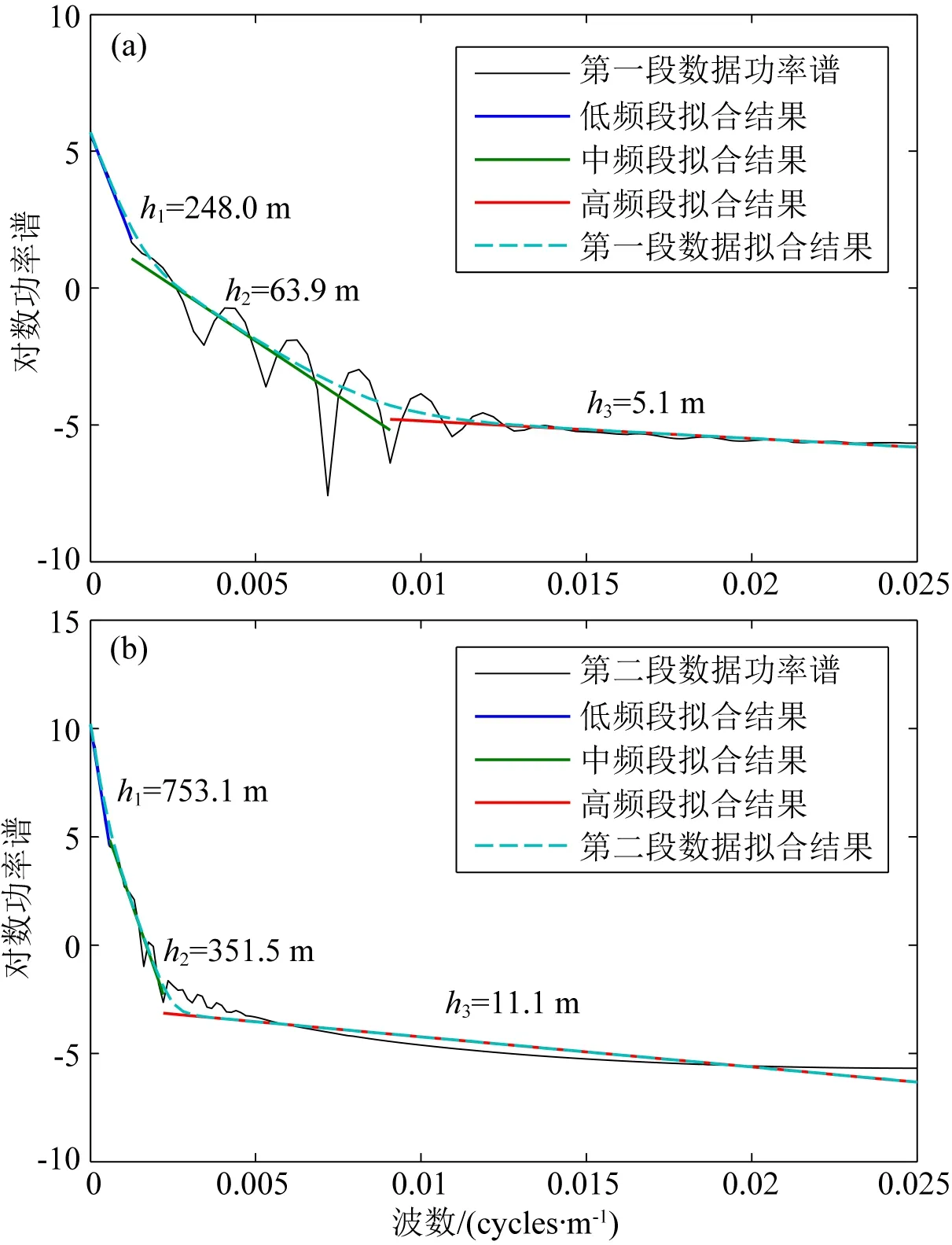
图10 实验2重力异常局部数据功率谱分析结果图

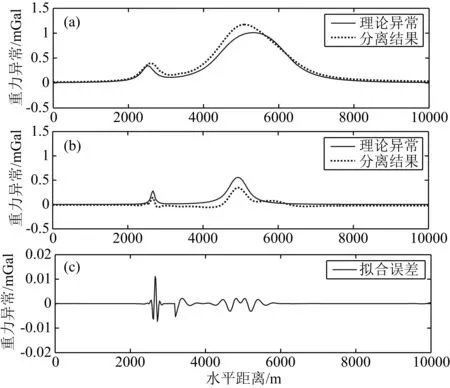
图11 实验2重力异常小波域优化位变滤波分离结果

对小波域优化位变滤波和频率域优化滤波分离出的区域异常与局部异常，分别计算其平均绝对误差和标准差，结果如表2所示.从表2可以看出，小波域优化位变滤波方法相对于频率域优化滤波方法能更好分离出区域异常和局部异常，前者分离结果优于后者.

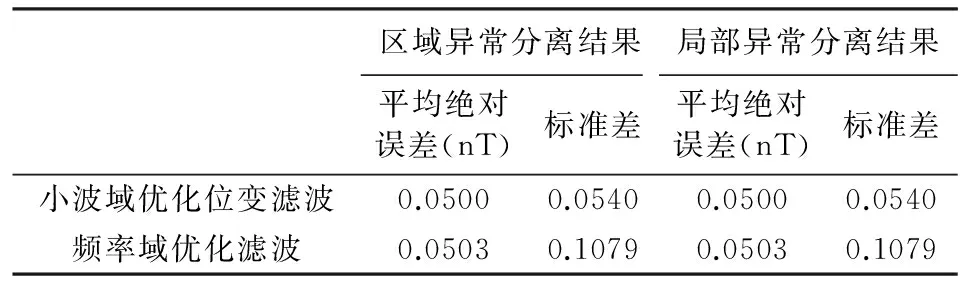
表2 实验2分离结果对比分析

实验2通过相对简单的模型试验，验证了小波域优化滤波方法的有效性.下面我们设计相对复杂的组合模型，检验频率混叠严重情况下小波域优化位变滤波的效果.

实验3：组合模型由七个水平无限延伸的长方体构成，各模型参数如表3所示.在地表测点间距20 m，剖面长度为10000 m，重力异常及模型分布剖面如图12所示.

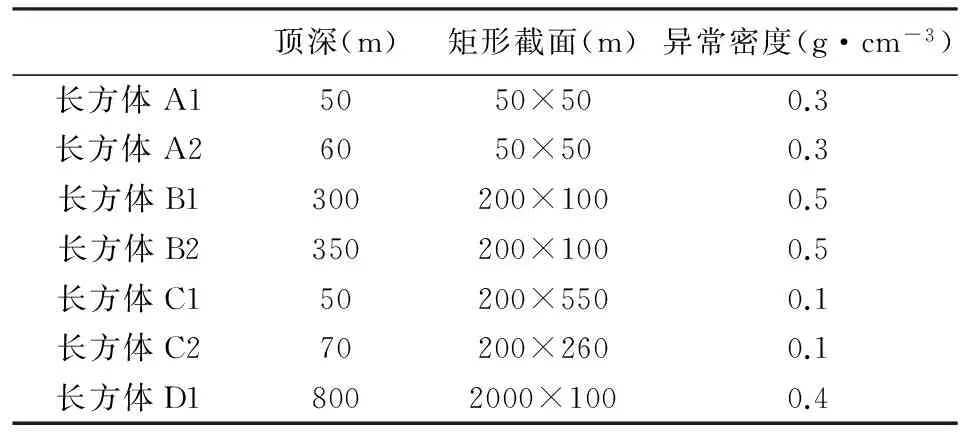
表3 实验3各模型参数表

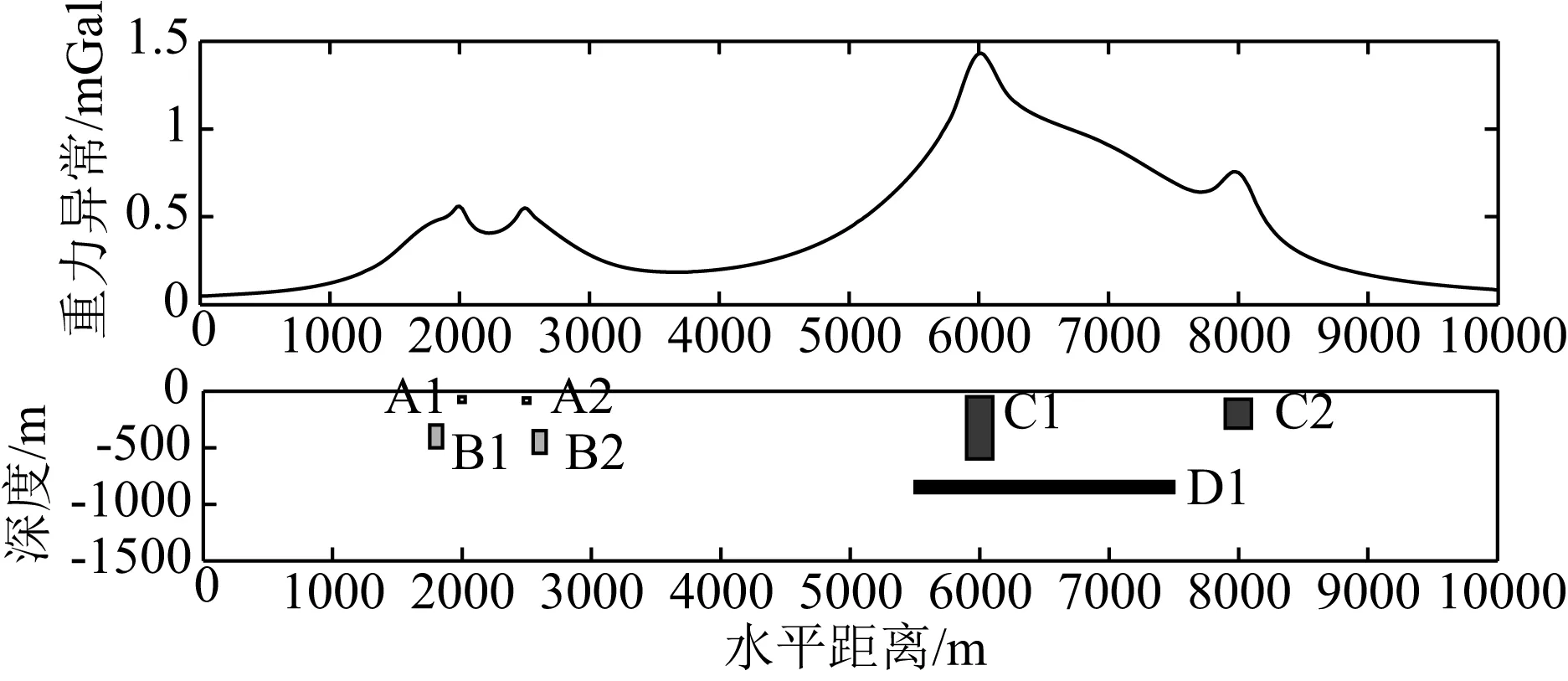
图12 实验3重力异常及其剖面图

从图12和表3可以看出，长方体C1从浅部向下延伸到深部，其顶深与A1、A2的相同，底深大于B1、B2的底深，可知其频谱会与A组、B组长方体的频谱重叠.对实验3重力异常数据进行功率谱分析，结果如图13所示，图中A、B、C、D四组长方体的功率谱相互重叠严重.

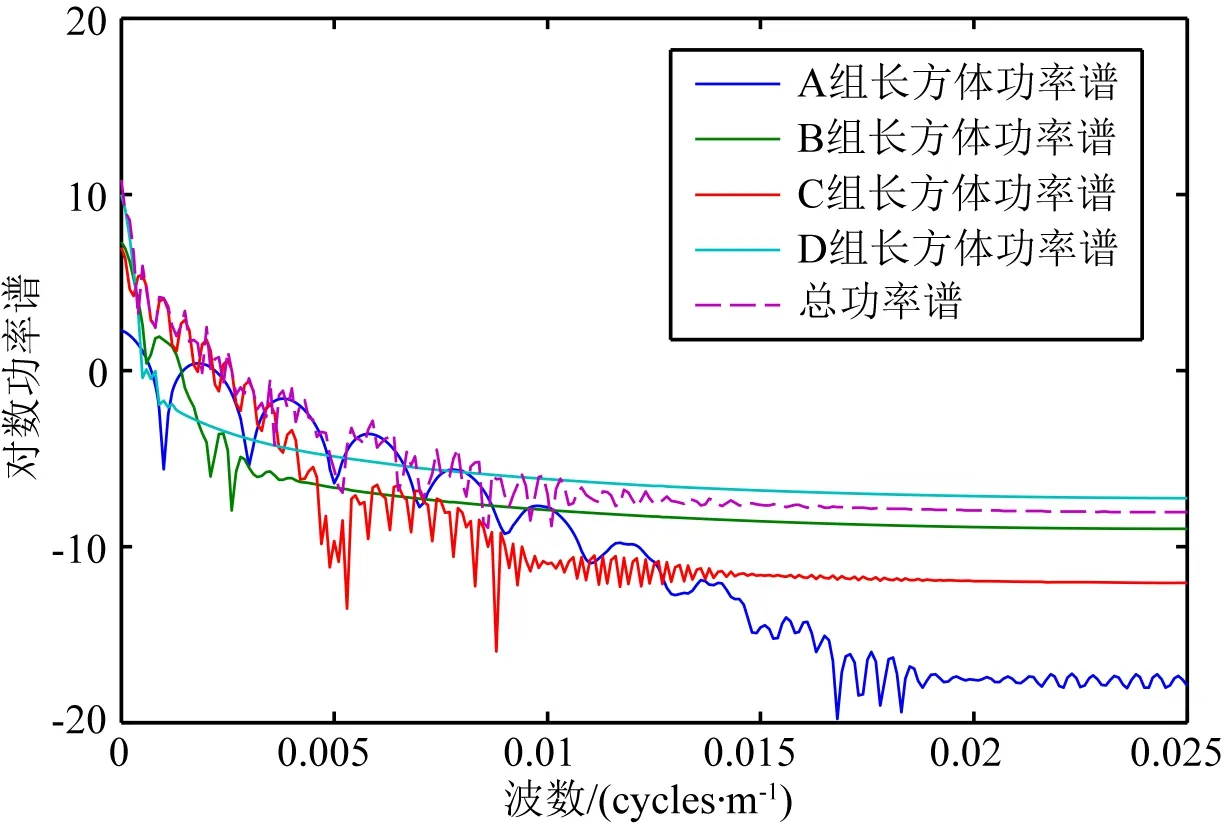
图13 实验3重力异常功率谱图

从图13可看出，模型实验3重力异常功率谱分为低频、中频、高频三个频段.采用频率域优化滤波方法进行线性拟合，其中，低频段波数为[0,0.0007]cycles·m-1，对应场源平均深度为840.5 m；中频段波数为[0.0007,0.0049]cycles·m-1，对应场源平均深度为141.4 m；高频段波数为[0.0049,0.025]cycles·m-1，对应场源平均深度为12.0 m.以此为指导，设计频率域优化滤波器.

模型实验3的频率域优化滤波法分离结果如图14所示.

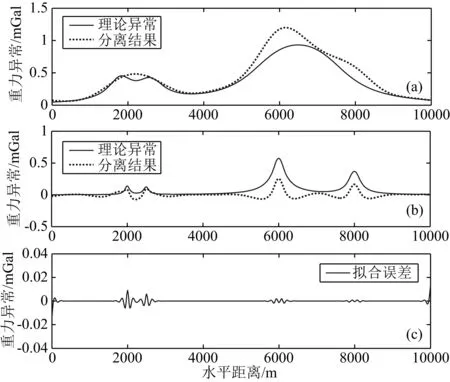
图14 实验3重力异常频率域优化滤波分离结果

从图14可以看出，分离出的区域异常（图14a）主要是B组和D组长方体的异常，同时含有少量的A组和C组长方体的异常；分离出的局部异常（图14b）主要是A组和C组长方体的异常.值得注意的是，在分离出的区域异常中（图14a），左侧呈单峰特征，不能分辨出两个B组的长方体，右侧由于残留的C组长方体的异常较多，曲线形态变形较大；相应的，在分离出的局部异常中（图14b），左侧曲线形态变化较大，右侧C组长方体的异常幅值衰减较大.

对模型实验3的重力异常数据进行小波变换时频分析，根据时频分析结果，将重力异常以x=4000 m为界分为前后两段局部数据.分别对两段局部数据进行功率谱分析，可识别出四个等效场源，平均场源深度分别为64.5 m、302.0 m、263.6 m、1214.7 m，与理论模型的A、B、C、D四组长方体相对应.以此为指导，设计小波域优化位变滤波器，模型重力异常分离结果如图15所示.

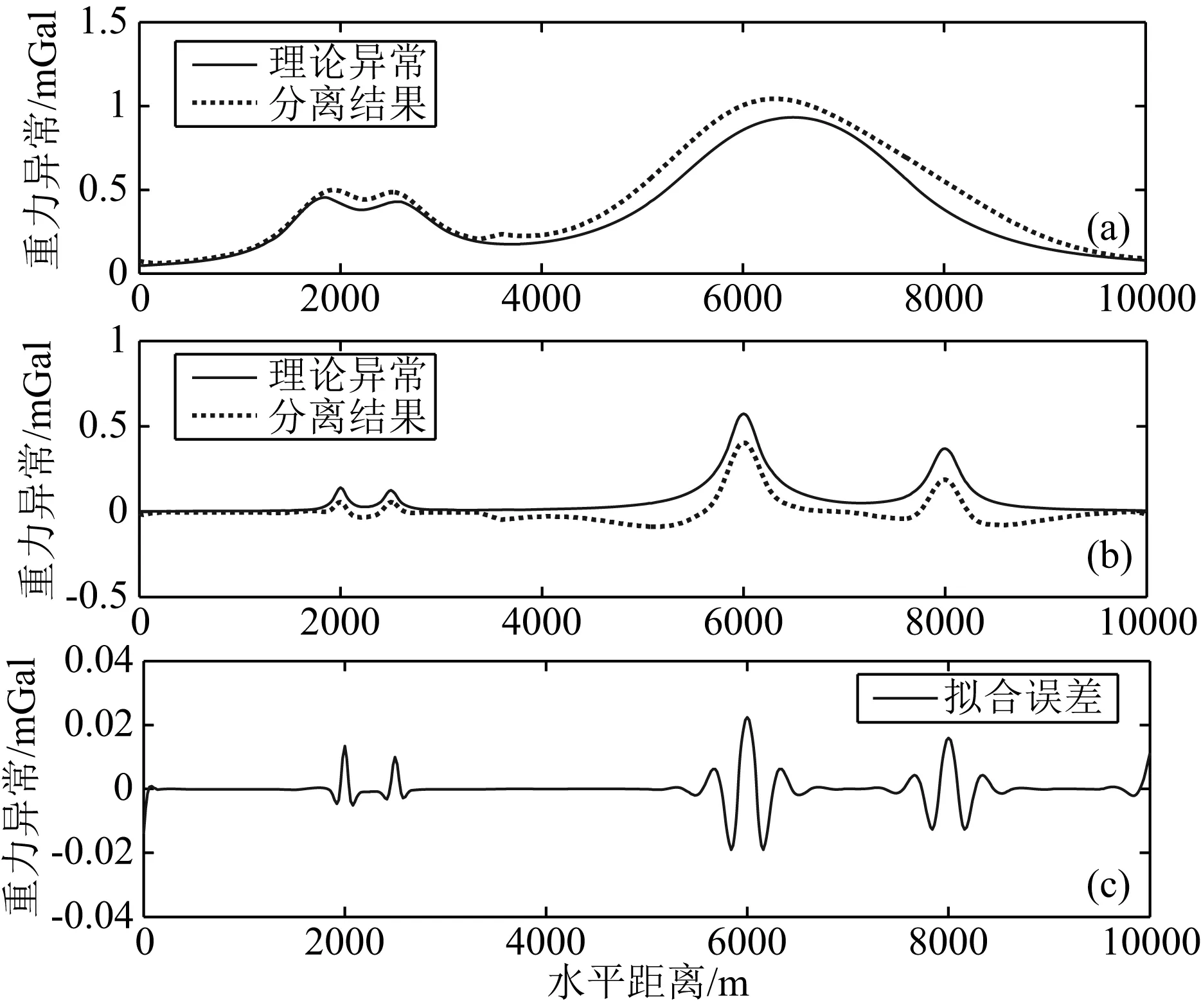
图15 实验3重力异常小波域优化位变滤波分离结果

从图15可以看出，分离出的区域异常（图15a）主要是B组和D组长方体的异常，局部异常（图15b）主要是A组和C组长方体的异常.在分离出的区域异常中（图15a），左侧呈双峰特征，能够很好地分辨出B1、B2长方体，右侧的曲线形态也与理论值一致；在分离出的局部异常（图15b）中，左侧A组长方体的异常曲线形态与理论值一致，仅幅值有所衰减，右侧C组长方体的异常曲线形态也与理论值相一致，且幅值衰减得到明显的改善.对比图14和图15可以看出，小波优化位变滤波的区域异常、局部异常分离结果明显优于频率域优化滤波.

分别计算两种方法分离结果的平均绝对误差和标准差，结果如表4所示.从表4可以看出，小波域优化位变滤波方法相对于频率域优化滤波方法能更

好分离出区域异常和局部异常，前者分离结果优于后者.

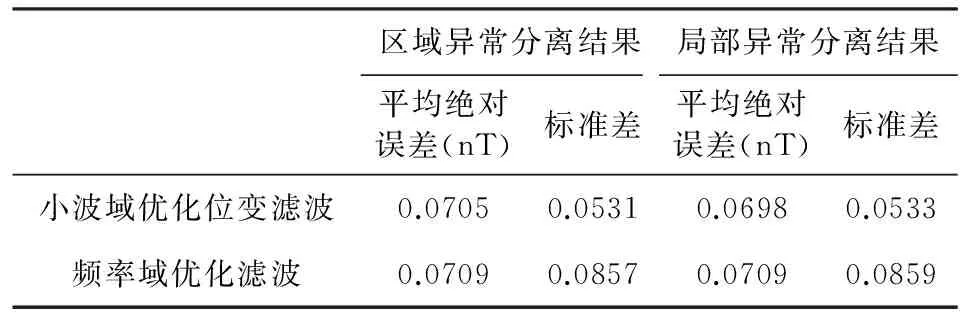
表4 实验3分离结果对比分析

从实验2和实验3重力异常分离实验结果可以看出，当局部数据频谱特征和全局数据频谱特征差异较大时，全局数据的频谱是所有场源信息综合影响的结果，经典的频率域分离方法会出现分离不彻底的问题.这种情况下，小波域优化位变滤波法具有一定优势，能根据局部数据的频谱特征动态调整滤波器参数，有效改善分离效果.

另一方面，当局部数据频谱与全局数据频谱差异很小时，小波域优化位变滤波方法将近似地退化为小波域优化滤波方法，由于小波域滤波误差的存在，其分离效果会略差于频率域优化滤波方法.

4 实测资料处理

实验4为某一重力异常剖面实测资料，在地表测点间距0.25 km，剖面长度为380 km，剖面重力异常如图16所示.

对实测资料数据分别用频率域优化滤波、Butterworth滤波和小波域优化位变滤波进行异常分离.

（1）频率域优化滤波

对实测剖面重力异常进行功率谱分析，结果如图17所示.

以此为指导，设计优化滤波器，频率域优化滤波法分离结果如图18所示.

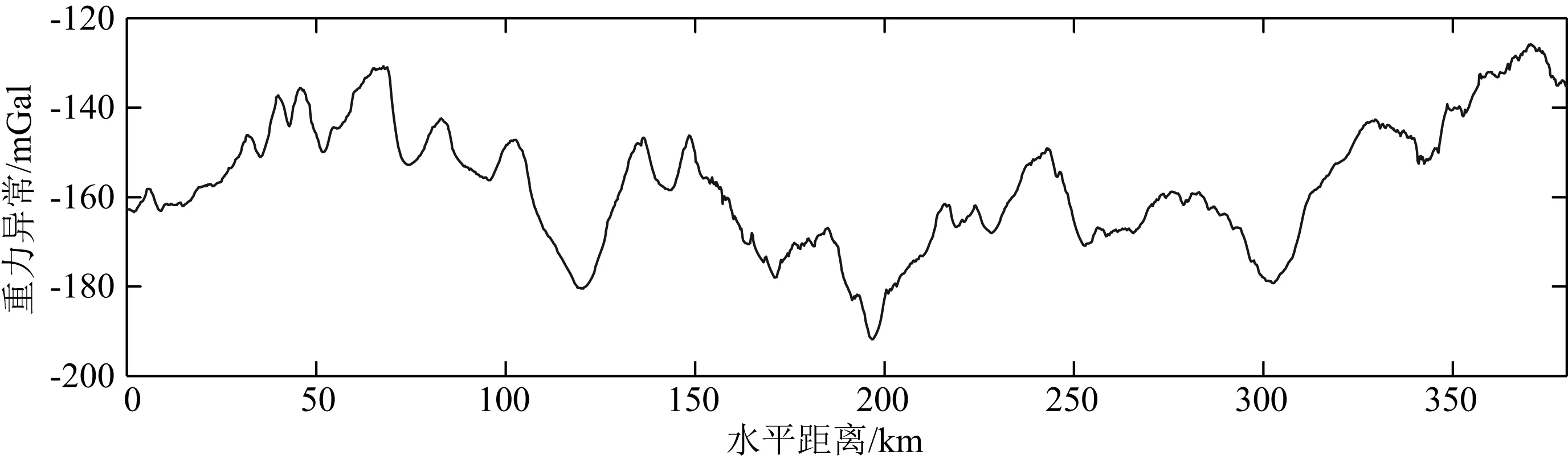
图16 实测数据剖面重力异常

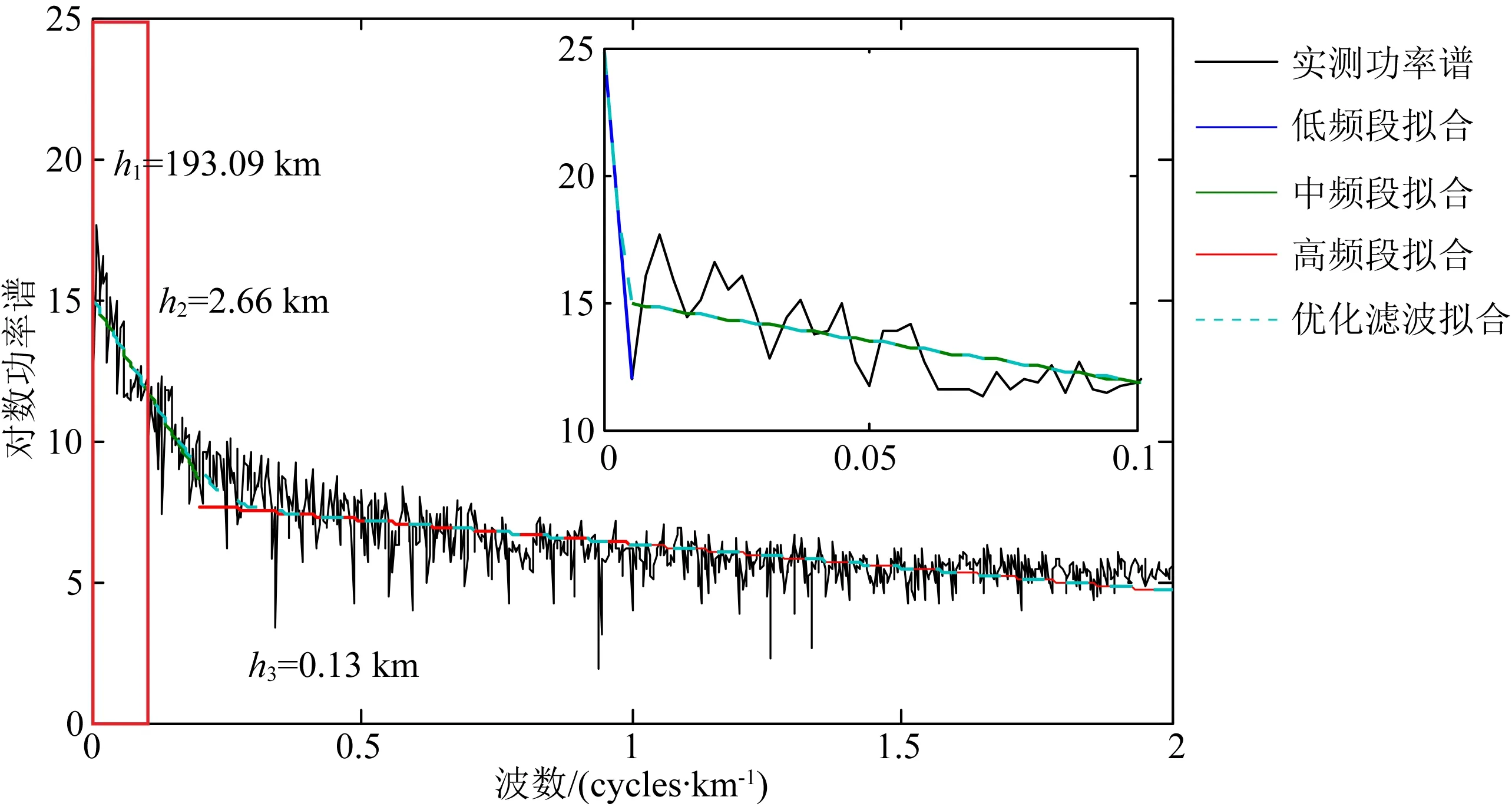
图17 实测剖面重力异常功率谱分析与优化滤波拟合

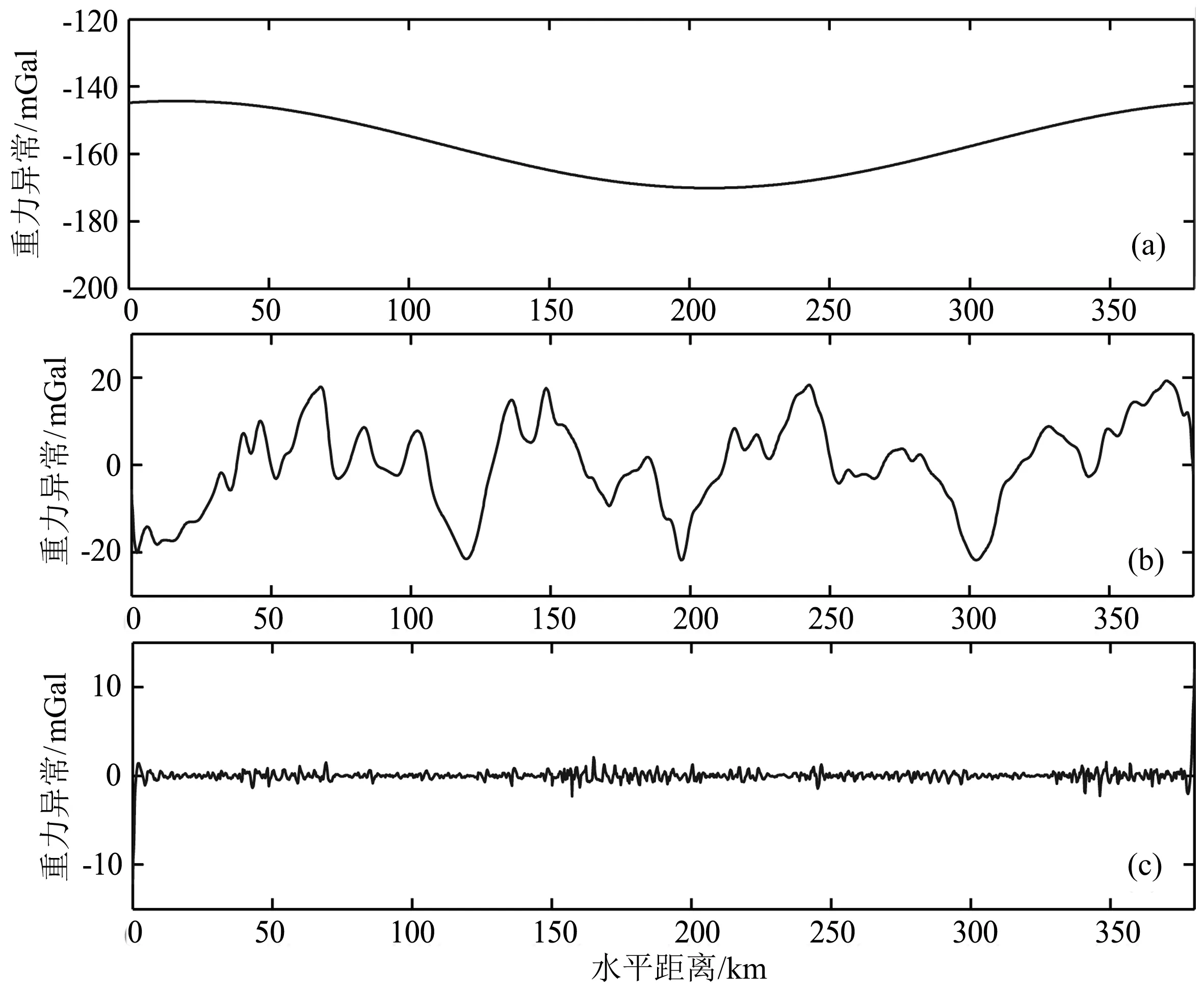
图18 实测剖面重力异常频率域优化滤波异常分离结果

（2）Butterworth滤波

作为对比，我们根据实测剖面重力异常功率谱分析结果（图17），设计Butterworth滤波器对实测剖面重力异常进行传统的频率域滤波分离，其中，低通截止频率为0.0053 cycles·km-1，高通截止频率为0.3 cycles·km-1，滤波器阶数为16，分离结果如图19所示.

从图18和图19可以看出，Butterworth滤波和频率域优化滤波分离结果相似，区域异常形态简单，仅反映出该剖面异常具有两边高、中间低的大尺度（波长大于180 km）特征；相应的，局部异常形态过于复杂，包含了波长从6 km到180 km的所有异常，局部异常分离结果不够理想.

（3）小波域优化位变滤波

对实测剖面重力异常进行小波变换时频分析，如图20所示.

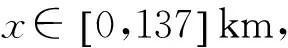
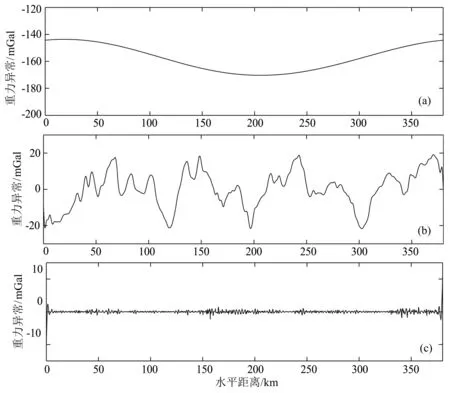
图19 实测剖面重力异常频率域Butterworth滤波异常分离结果

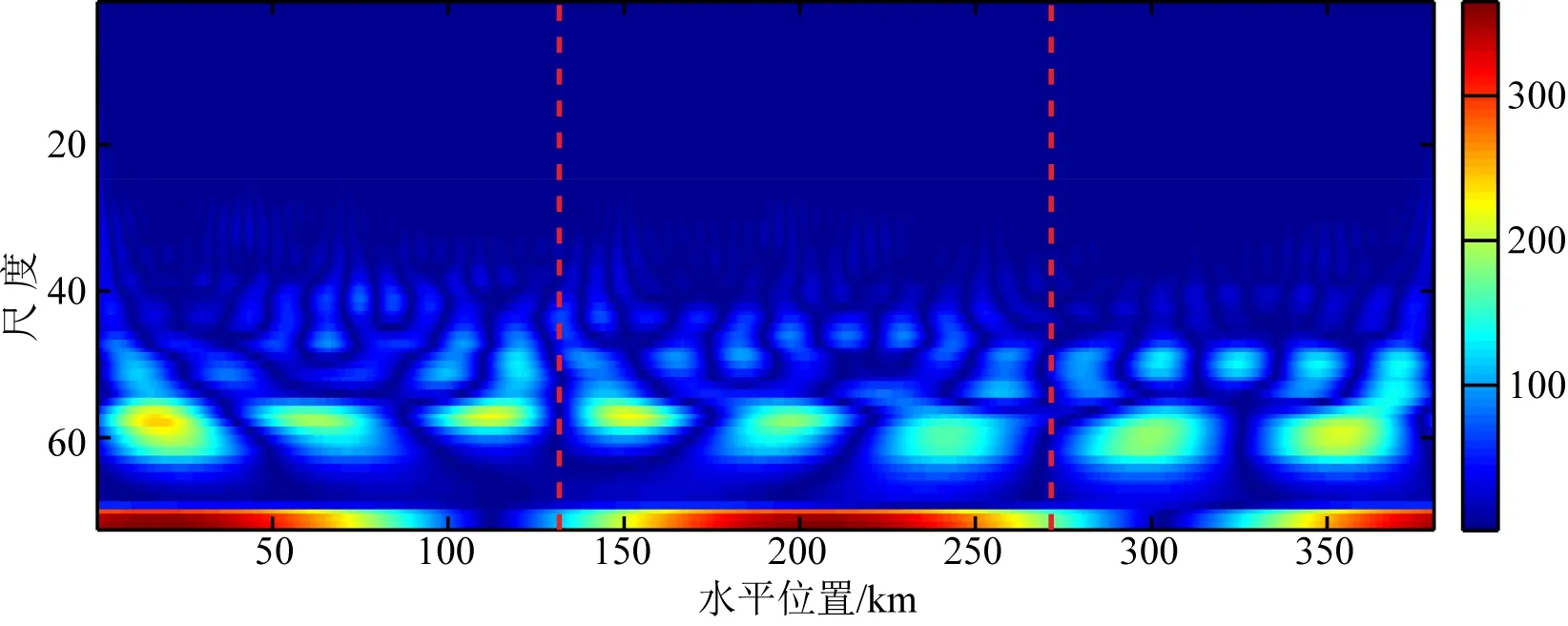
图20 实测剖面重力异常小波变换时频分析图

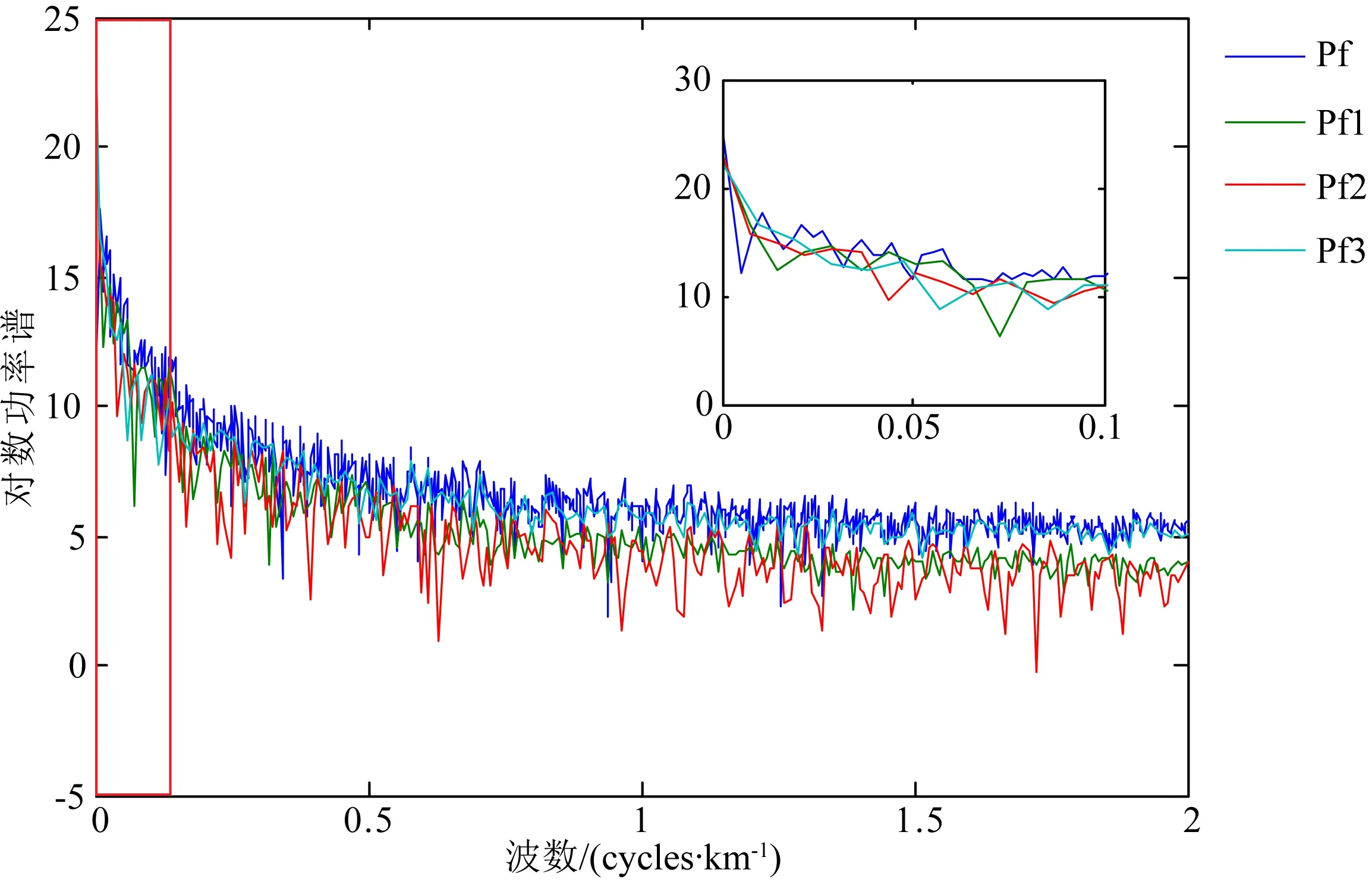
图21 全局数据与局部数据功率谱分析对比图

对分段后的实测剖面重力异常分别进行功率谱分析，并分段线性拟合，按照本文2.3节所述的方法设计小波域优化位变滤波器.实测剖面重力异常分离结果如图22所示.

从图22可以看出，小波域优化位变滤波分离结果中，区域异常信息丰富，不仅反映出该剖面异常所具有的两边高、中间低的大尺度特征，还包含较多的中等尺度异常；相应的，局部异常则分辨得更加清晰，仅含有小尺度的浅部场源异常.

图23是实测剖面重力异常密度反演结果图.对比图18、图19和图23则会发现，频率域Butterworth滤波和优化滤波分离出的区域异常过于简单，与反演结果不能很好的对应，而局部异常中残留有较多区域异常，既包含深度小于10 km的浅部场源异常，又包含深度10～50 km的深部场源异常.

对比图22和图23可以看出，小波域优化位变滤波分离出的区域异常与反演结果中深度大于10 km的场源分布规律一致，局部异常与反演结果中深度小于10 km的场源分布规律一致，小波域优化位变滤波的分离结果与反演解释结果吻合得相当好.

以上三种方法均对实测剖面重力异常分高、中、低三个频段进行分离，以便客观对比三种方法的分离效果，实验结果体现了小波域优化位变滤波法的优越性.值得指出的是，由于采用的频段数较少，分离结果仍可进一步进行分解，例如，小波域优化位变滤波分离出的区域异常（见图22a）仍然含有更深场源对应的低频成分.再次采用小波域优化位变滤波方法对其进行滤波分离，得到结果如图24所示.

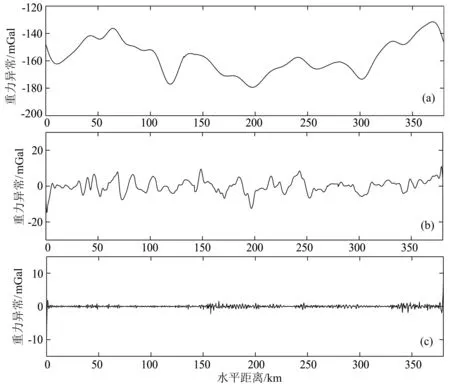
图22 小波域优化位变滤波分离结果

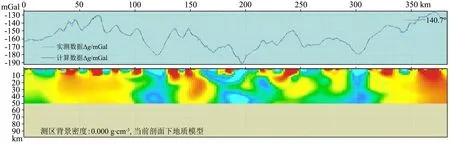
图23 实测剖面重力异常反演解释成果图

由图24可以看出，小波域优化位变滤波所得区域异常的二次低通滤波结果与深度≥45 km的更深场源相对应；二次高通滤波结果与反演结果中深度10～45 km场源之间的对应关系更加明显.

对频率域优化滤波分离所得局部异常（见图18b）进行二次分离，结果如图25所示.

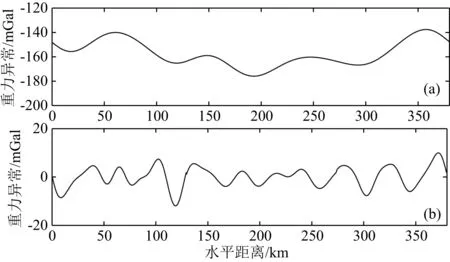
图24 小波域优化位变滤波所得区域异常的二次分离结果

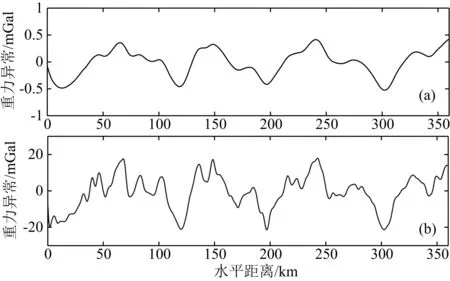
图25 频率域优化滤波所得局部异常的二次分离结果

从图25可以看出，频率域优化滤波所得局部异常的二次低通滤波结果与反演结果中深度10～50 km的场源分布规律一致，但幅值太小.因而，在二次高通滤波结果中，仍然残留较多的低频成分，与反演结果中浅部场源对应关系不太明显.

从实测资料分离实验结果可以看出，不论是采用低、中、高频三个频段进行异常分离还是对分离后的结果进行二次分离，小波域优化位变滤波方法的分离结果均优于频率域优化滤波和Butterworth方法.

5 结论

本文在小波域滤波理论和优化滤波方法的基础上，研究提出小波域优化位变滤波方法，该方法具有空间变化滤波能力，在不同空间位置表现出不同的滤波器特性，适用于局部数据频谱与全局数据频谱存在较大差异的重力异常分离问题.理论模型重力异常分离实验表明，在局部数据频谱与全局数据频谱差异较大时，该方法相对于频率域优化滤波法具有一定优势.实测资料分离实验结果表明，该方法分离结果优于频率域优化滤波和Butterworth滤波方法，与反演解释成果吻合得更好.

小波域位变优化滤波方法提供了设计小波域位变滤波器的有效途径，该方法可应用于其他需要位变滤波的位场数据处理领域.需要指出的是该位变滤波法会在分块边界处出现一定程度的阶跃现象，有的时候需要对边界附近的分离结果进行平滑滤波以消除阶跃现象，这是下一步实用化方面需要完善的地方.

An Y L, Guan Z N. 1985. The regularized stable factors of removing high frequency disturbances.ComputingTechniquesforGeophysicalandGeochemicalExploration（in Chinese）, 7（1）: 13-23.

Fedi M, Quarta T. 1998. Wavelet analysis for the regional-residual and local separation of potential field anomalies.GeophysicalProspecting, 46（5）: 507-525.

Guo L H, Meng X H, Shi L, et al. 2012. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent.ChineseJ.Geophys. （in Chinese）, 55（12）: 4078-4088, doi: 10.6038/j.issn.0001-5733.2012.12.020.

Gupta V K, Ramani N. 1980. Some aspects of regional-residual separation of gravity anomalies in a Precambrian terrain.Geophysics, 45（9）: 1412-1426.

Hou Z C. 1981. Filtering of smooth compensation.GeophysicalProspectingforPetroleum（in Chinese）, （2）: 22-29. Kaiser G. 1996. Wavelet filtering in the scale domain.∥ Proceedings of the SPIE 2762, Wavelet Applications III. Orlando, FL: SPIE.

Keating P, Pinet N. 2011. Use of non-linear filtering for the regional-residual separation of potential field data.JournalofAppliedGeophysics, 73（4）: 315-322.

Li Z S. 2006. Study of the new high order Butterworth optimum transfer function.JournalofHuaqiaoUniversity（NaturalScience） （in Chinese）, 27（2）: 174-176.

Pawlowski R S, Hansen R O. 1990. Gravity anomaly separation by Wiener filtering.Geophysics, 55（5）: 539-548.

Pawlowski R S. 1994. Green′s equivalent-layer concept in gravity band-pass filter design.Geophysics, 59（1）: 69-76.

Ridsdill-Smith T A. 1998. Separating aeromagnetic anomalies using wavelet matched filters.∥ Proceedings of the 68th Annual International Meeting, SEG, Expanded Abstracts. 550-553.

Spector A, Grant F S. 1970. Statistical models for interpreting aeromagnetic data.Geophysics, 35（2）: 293-302.

Xiong G C. 1979. Spatially varying filtering and its application to interpretation of gravity and magnetic anomalies.GeophysicalandGeochemicalExploration（in Chinese）, 3（5）: 43-49.

Xiong G C, Zhang F R. 1981. Spatially varying filter.GeophysicalandGeochemicalExploration（in Chinese）, 5（4）: 205-213.

Yang W C, Shi Z Q, Hou Z Z, et al. 2001. Discrete wavelet transform for multiple decomposition of gravity anomalies.ChineseJ.Geophys. （in Chinese）, 44（4）: 534-542.

附中文参考文献

安玉林, 管志宁. 1985. 滤除高频干扰的正则化稳定因子. 物化探计算技术, 7（1）: 13-23.

郭良辉, 孟小红, 石磊等. 2012. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用. 地球物理学报, 55（12）: 4078-4088, doi: 10.6038/j.issn.0001-5733.2012.12.020.

侯重初. 1981. 补偿圆滑滤波方法. 石油物探, （2）: 22-29.

李钟慎. 2006. 新型高阶Butterworth最佳传递函数. 华侨大学学报（自然科学版）, 27（2）: 174-176.

熊光楚. 1979. 位变滤波及其在重磁异常解释中的应用. 物探与化探, 3（5）: 43-49.

熊光楚, 张福荣. 1981. 位变滤波器. 物探与化探, 5（4）: 205-213.

杨文采, 施志群, 侯遵泽等. 2001. 离散小波变换与重力异常多重分解. 地球物理学报, 44（4）: 534-542.

（本文编辑 何燕）

Preferential spatially varying filtering method in the wavelet domain for gravity anomaly separation

LIU Cai-Yun1, 2, YAO Chang-Li2*, ZHENG Yuan-Man2

1SchoolofMathematicsandInformation,YangtzeUniversity,HubeiJingzhou434023,China2SchoolofGeophysicsandInformationTechnology,ChinaUniversityofGeosciences,Beijing100083,China

The classical frequency domain filtering method for gravity anomaly separation cannot change its frequency response at different spatial positions to adapt the frequency characteristic of local data, for the reason of lacking spatial information with Fourier transform. A preferential spatially varying filtering method in the wavelet domain （PSVF-WD） is proposed based on the scaling filtering theory and preferential filtering method, in order to overcome the limitation of the classical frequency domain filtering method mentioned above.This method uses a preferential spatially varying filter to separate gravity anomalies. Firstly, it segments gravity anomaly data into several blocks after analyzing the spatial distribution characteristics of frequency components with the wavelet analysis method. Secondly, it obtains the local translation function with the preferential filtering method and calculates the local equivalent coefficients with the method derived in this paper. Thirdly, it combines the local equivalent coefficients to global ones according to the position information of them and achieves the design of PSVF-WD. Lastly, it obtains separated gravity anomalies using the global equivalent coefficients of PSVF-WD and wavelet coefficients of gravity anomalies.We test the PSVF-WD with gravity-anomaly separation experiments of three synthetic data and one real data. In experiment 1, the PSVF-WD separates the composite signal of four different frequency sinusoidal signals using low-high filtering at one time. The results of this experiment show the spatially varying filtering ability of PSVF-WD. In experiment 2, the synthetic model consists of four prisms. Two of them belong to a relatively shallower layer and the other two of them belong to relatively deeper layer. However, one prism of the relatively shallower layer is deeper than another prism of the relatively deeper layer. The PSVF-WD method separates the anomalies of the relative shallower layer and deeper layer pretty well, while the preferential filtering method only separates the anomalies of the shallowest prism and remains anomalies of the rest of three prisms together. The average absolute error and standard deviation of separation results are 0.0500 nT and 0.0540, respectively for SVF-WD, while they are 0.0503 nT and 0.1079, respectively for preferential filtering. In experiment 3, the synthetic model consists of one large horizontal prism, one large vertical prism and five small prisms with different depths. The problem is more complicated because the spectrum aliasing is serious. The regional-residual separation results of PSVF-WD method are pretty well, but regional anomalies separated by the preferential filtering method still have too many residual anomalies and deform severely. The average absolute error and standard deviation of separation result are 0.0705 nT and 0.0531, respectively, while they are 0.0709 nT and 0.0867, respectively for preferential filtering.In the field data separation experiment with the PSVF-WD method, the separated regional anomalies contain large- and middle- scale anomalies, which correspond to the field sources deeper than 10 km described in inversion results, and the separated residual anomalies contain small-scale anomalies, which correspond to the field sources shallower than 10 km described in inversion results. In the experiments with preferential filtering and traditional Butterworth filtering, the separated regional anomalies are both too simple and do not correspond to inversion results very well, and the separated residual anomalies both contain too many regional anomalies.The proposed PSVF-WD method has the ability of spatially varying filtering, and is suitable for separating the gravity anomalies whose spectrum of local data is different from the average spectrum of global data obviously. The results of synthetic and field data separation experiments show that the proposed PSVF-WD method is superior to the classical frequency domain methods such as Butterworth filtering and preferential filtering method when the spectrum of local data is different from the average spectrum of global data obviously. In sum, this paper provides an approach to design a spatially varying filter in the wavelet domain, which can be applied to the other spatially varying filtering fields in potential data processing.

Anomaly separation; Wavelet domain; Preferential filtering; Spatially varying filtering; Gravity anomaly

国家高技术研究发展计划（863计划）课题（2014AA06A613），国家自然科学基金项目（61273179），湖北省教育厅科学技术研究项目（D20131206）联合资助.

刘彩云，女，1975年生，博士、副教授，主要从事小波分析、重磁勘探和应用数学等方面的教学和科研工作. E-mail: liucaiyun01@hotmail.com

*通讯作者 姚长利，男，1965年生，教授，博士生导师，主要从事重磁勘探方法技术研究.E-mail: clyao@cugb.edu.cn

10.6038/cjg20151234.

10.6038/cjg20151234

P631

2014-12-01，2015-09-30收修定稿

刘彩云， 姚长利， 郑元满. 2015. 重力异常分离的小波域优化位变滤波方法.地球物理学报，58（12）:4740-4755,

Liu C Y, Yao C L, Zheng Y M. 2015. Preferential spatially varying filtering method in the wavelet domain for gravity anomaly separation.ChineseJ.Geophys. （in Chinese）,58（12）:4740-4755,doi:10.6038/cjg20151234.