一种高效的多足机器人足端力分配计算方法*

曾 怡，郭祖华，赵士杰

(北京航空航天大学，北京 100191)

0 引言

对于多足机器人而言，至少有三条腿支撑才能保持机体稳定，每个足端反力有3个分量。但对于一个移动机器人而言，只能列出6个平衡方程，无法解得唯一的解，这个问题被称为力/力矩的分配问题［1-7］。国内外许多学者对此问题进行了研究，归纳起来主要有两种解决方法。第一种方法即伪逆法。V．Kumar［2］采用螺旋理论列出了多肢体系统的平衡方程，根据伪逆的思想，推导了足端支反力的求解公式，该方法没有考虑摩擦约束。J．F．Gardner［3］通过实验结果补充了两个有关摩擦力的方程，同样利用伪逆理论进行求解，该方法得到的结果不能保证机器人关节的控制力矩最优。第二种方法即优化法。Mustafa Suphi Erden［4］和王新杰［5］都推导了以关节力矩为变量的动力学方程、摩擦约束方程，分别以关节力矩平方和最小、电机所需功率总和最小为目标函数，进行优化求解，使得机器人关节力矩达到最小。该方法克服了文献［3］中的问题，但计算费时。此外，H．Y Liu［6］补充了三个与足端反力有关的线性方程，实现了解析求解，计算速度快，由于忽略了一些约束条件，得到的关节力矩较大。本文中提出一个新的力分配算法，在求解模型中考虑了机器人动力学模型和足端的摩擦条件，然后对方程组进行线性化处理，得到一组关于关节力矩的线性方程组，然后采用伪逆法求解该方程组，该方法求解得结果既保证了关节力矩最小，又保证了高的计算效率。

1 计算模型

这类问题中的约束条件和接触反力有关，故将这些非线性等式约束用一组非线性方程组抽象表达为:

式中:f为支反力向量。

利用Newton-Euler建立动力学方程，然后改变动力学方程形式，简记成如下形式:

式中:τ为关节力矩向量;A，C为系数矩阵。

把式(3)代入式(1)中，有:

对于方程(4)利用泰勒公式展开，在初值τ0附近取一阶近似对原方程进行线性化处理:

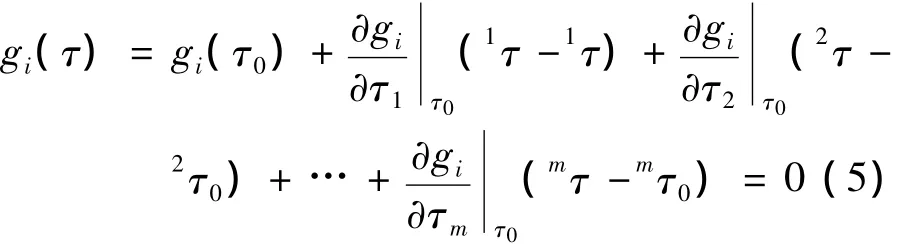
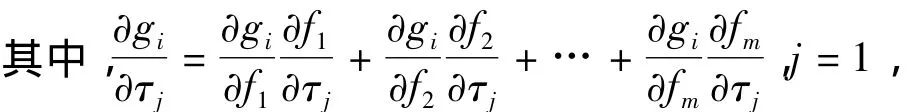
…，m;m为关节力矩向量τ的维数;i为约束方程的个数。

把方程(5)写成矩阵的形式如下:

把式(3)代入式(2)中，得:

简记作:

由式(7)和式(9)组合，得:

方程(10)包含了动力学约束Aτ和非线性约束G。其中，Aτ为n×m的矩阵。假设补充的方程个数为m-n，那么方程(10)有唯一解。如果补充方程的个数小于m-n，则利用伪逆理论求具有最小范数的解。

由方程(6)可知，初值的选择是一个关键的问题。如果初值的较为准确，求解过程收敛速度将很快。通过循环迭代解决初值问题，跌代过程如下。

随意给定初始值τ0;利用伪逆理论求解τ;计算|τ-τ0|，如果小于ε，退出循环。否则，跳转把τ赋给τ0，回到式(2)继续计算。

在机器人行走过程中，只需要在第一时间步时通过上述循环计算出τ0，然后计算τ。在下一时刻，只须用上一时刻的τ作为初值τ0进行当前时刻的关节力矩计算，而不再需要跌代，这可以使计算速度大为提高，而且计算结果足够精确。

2 计算实例

笔者以机器人三条腿支撑情况为例验证新算法。现给出六足机器人的模型和结构参数，如图1和表1所示。

图1 一条腿的坐标系示意图

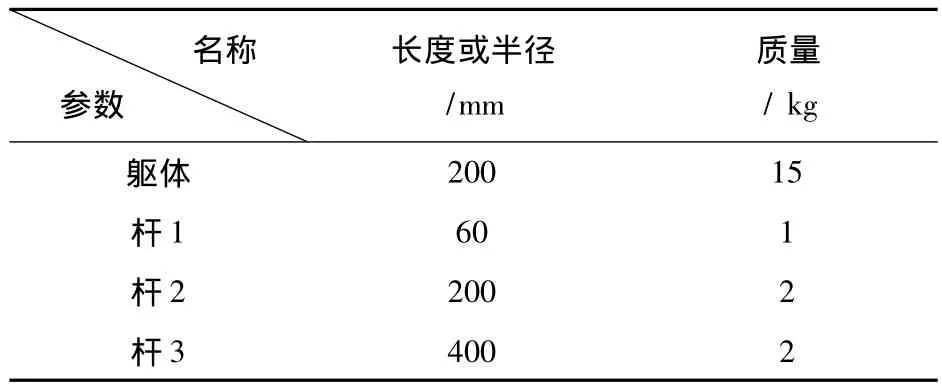
表1 躯体及杆件的设计参数

此时只有6个平衡方程，但有9个未知量。现引用文献［1］的补充方程:

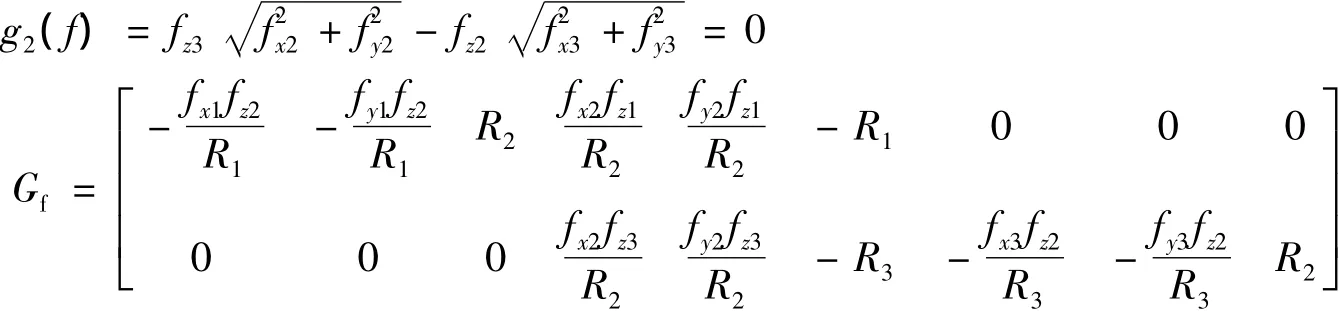
其中:fxi，fyi，fzi，i=1，2，3 为足端反力的三个分量。

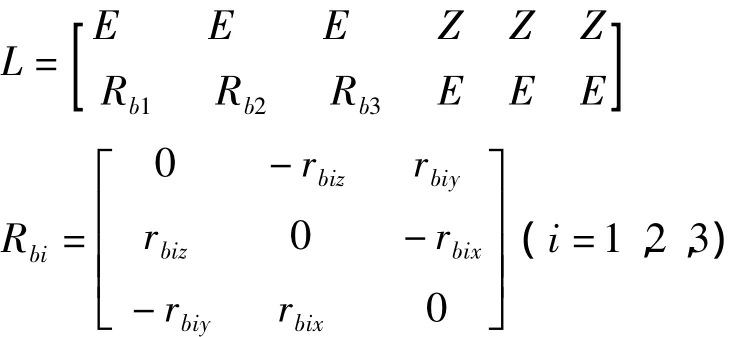
F、M为躯体的惯性力/力矩减去迈步腿对躯体作用的力/力矩所得的支撑腿对躯体作用的力/力矩。

图3显示了三种不同方法求得的三个支撑足的足端支反力大小，结果显示，三种方法求得的结果变化趋势一致，其中伪逆法求得的支反力大小略小，另外两种方法求得的支反力大小几乎完全一样。

图4给出了三种算法求得的每条支撑腿足端反力的切法比系数。结果显示，伪逆法求得的切法比系数非常小，小于10-3。而优化法和新算法求出的切法比系数大小相当，都在0．15左右，满足足端不打滑的约束条件。

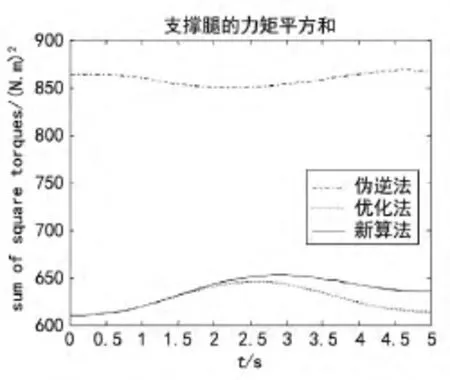
图2 支撑腿关节力矩的平方和

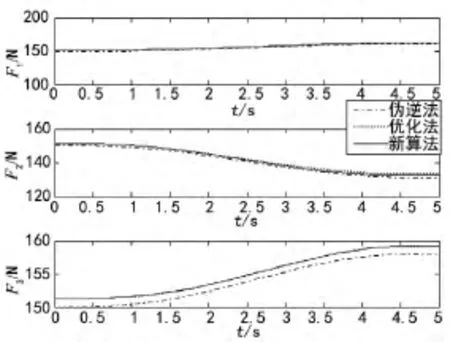
图3 三个支撑腿的足端力变化

图4 三支撑腿支反力比率的变化

图5 显示了机器人单步行走时，三条支撑腿的力矩大小变化。其中最左侧的一列是各腿关节1的力矩，最右侧的一列是各腿关节3的力矩。从图中可以看出，由于伪逆法和优化法、新算法追求的目标不一样，所以得到的各关节力矩有较大区别。用伪逆法求得的结果显示各条腿关节1和关节3的力矩很小，而关节2的力矩很大;用优化法和新算法求得的结果也是关节1和关节3的力矩小，关节2的力矩大，但差别没有那么显著。另外，用优化法和新算法得到的结果有所差别，关节1的力矩差别比较大，但数值都比较小。关节2和关节3的力矩变化趋势一致，大小略有不同。结合图2可以看出，使用用不同的力分配方法，在采用相同的步态行走一步时，机器人各个关节的力矩平方和的不同，图中2显示新方法的力矩与优化法类似但明显优于传统伪逆法，所以可以推测新方法可以使机器人的总体能耗小于传统伪逆法。利用优化法和新算法求解机器人单步行走关节力矩大小时，记录了两种算法的求解时间。优化法耗时5 019 ms，新算法耗时21 ms，可见新算法的计算效率比优化法高很多，可用于实时控制。

图5 支撑腿9个关节力矩的变化

3 结论

本文提出了一种新的多足机器人足端反力的求解方法。在求解模型中考虑了机器人动力学平衡和足端的摩擦条件，然后对方程组进行线性化处理，得到一组关于关节力矩的线性方程组，然后采用伪逆法求解该方程组。本文以六足机器人三条腿支撑为例，利用伪逆法、优化法和新算法求解机器人一步行走过程中的关节力矩大小。从计算结果来看，伪逆法得到的结果偏于保守，能耗较大，而优化法和新算法得出的关节力矩比较小，保证了机器人能耗较小。从计算时间上看，新算法求解速度快，用时短，计算效率高，优于优化方法。因此，用新算法得到的力/力矩分配方案既保证了关节力矩最小，又保证了高的计算效率，可用于实时控制。

［1］ Cheng Fan-Tien，Orin David E．Efficient Algorithm for Optimal Force Distribution-The Compact-Dual LP Method［J］．IEEE Transactions on Robotics and Automation，1990，6(2):178-187．

［2］ V．Kumar，K．J．Waldron．Force Distribution in Closed Kinematic Chains［J］．IEEE Journal of Robotics and Automation，1988，4(6):657-664

［3］ J．F．Gardner．Efficient Computation of Force Distributions for Walking Machines on Rough Terrain［J］．Robotica，1992，10(5):427-433．

［4］ Mustafa Suphi Erden，Kemal Leblebicioõglu．Torque Distribution in a Six-Legged Robot［J］．IEEE Transactions on Robotics，2007，23(1):179-186．

［5］ 王新杰．多足步行机器人运动及力规划研究［D］．武汉:华中科技大学，2005．

［6］ H．Y．Liu，B．C．Wen．Force Distribution for the Legs of a Quadruped Walking Vehicle［J］．Journal of Robotic Systems，1997，14(1):1-8．

［7］ 赵士杰．六足机器人运动轨迹规划［D］．北京:北京航空航天大学，2014．