基于四元数的四旋翼飞行器姿态解算算法
2015-05-11谌海云岑汝平
蒋 钰,谌海云,岑汝平
(1.西南石油大学 电气信息学院,成都 610500;2.西南石油大学 电气信息学院,成都 610500;3.西南石油大学 电气信息学院,成都 610500)
基于四元数的四旋翼飞行器姿态解算算法
蒋 钰1,谌海云2,岑汝平3
(1.西南石油大学 电气信息学院,成都 610500;2.西南石油大学 电气信息学院,成都 610500;3.西南石油大学 电气信息学院,成都 610500)
0 引言
四旋翼飞行器是一种能垂直升降的微型飞行器,它能够完成近地侦察、监视等任务,具有广泛的军事、民事等应用前景,其所拥有的巨大吸引力鼓舞着科研人员不懈地进行各种研究和开发。但是四旋翼飞行器的控制难度较大,难点主要是因为飞行器具有欠驱动、多变量这些比较复杂的特性[1]。因此四旋翼飞行器的姿态控制也成为了控制领域的热点和难点。四旋翼飞行器的姿态控制是飞行器总体设计的重要组成部分,我们常说的飞行器飞行的“好坏”指的就是飞行器飞行时的姿态效果。实现飞行器飞行姿态的控制有多种方法,如欧拉角、方向余弦、四元数法等。
1 欧拉角算法
飞行器在飞行过程中相对于水平面发生了一定角度的倾斜,此时我们不能直观的说飞行器倾斜了多少角度,因为物体的运动是合运动,我们可以把它的运动矢量正交分解为几个运动的合成。同理,我们把飞行器的旋转分解为三个轴上的旋转,这个旋转的角度就是欧拉角[2],如图1所示,图中α、β、γ就是欧拉角。
1.1 坐标系
飞行器飞行的参数必须在一个确定的坐标系下才能进行描述。对于飞行器来说常用的坐标系有地理坐标系和机体坐标系。

图1 α、β、γ三个欧拉角
1)地面坐标系(OEXEYEZE)
地理坐标系一般选用地轴系。原点O设在地面上的某一点,OEXE轴指向正北方向,OEYE轴指向正东方向,OEZE轴与XEOEYE平面垂直,方向为垂直向上。
2)机体坐标系(OXYZ)
机体坐标系是固定在飞行器身上并与之一起移动的动态坐标系。原点O为飞行器重心,OX轴与机身轴线平行并规定指向机头方向为正方向,相对OX轴顺时针旋转90°为OY轴,OZ轴垂直XOY平面向上。
当我们的飞机头朝北水平放置时载体坐标系和参考坐标系是重合的,那么接下来我们绕飞机的Z轴旋转30°,这个旋转的欧拉角就是我们所说的Yaw,同样,绕飞机的Y轴旋转30°,我们得到Pitch,绕飞机X轴旋转得到Roll。
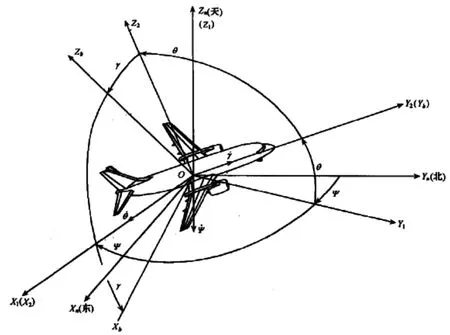
图2 两个坐标系
1.2 欧拉角微分方程

式中xω、yω、zω三个角速度分量可由直接安装在飞行器上的三个角速度陀螺仪测量出来,可以认为是已知量。因此,求解这个微分方程式就可以直接得到飞行器的三个欧拉角。
2 四元数
由于方向余弦方程的计算量较大,工作效率很低,因此我们采用四元数法实时解算姿态角[3]。四元数(Quaternions)是威廉·卢云·哈密尔顿(William Rowan Hamilton,1805-1865)1843年在爱尔兰发现的数学概念。
2.1 四元数表达式
四元数由一个实数和三个虚数构成,所以是一个四维空间的向量,但是它的三个虚数又有三维空间的性质[4]。因此,三维空间中的一个矢量,可以看作一个实部为0的四元数,这个四元数是这个三维空间的一个矢量在四维空间里的“映像”,或者叫做这个矢量的“四元数映像”。这样,我们就把三维空间和一个四维空间联系起来,用四维空间中四元数的性质和运算规律来研究三维空间中刚体定点转动的问题。四元数有如下四种表示方式:
1)矢量式:
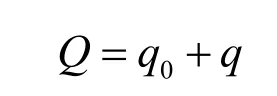
q0为四元数Q的标量部分,q为Q的矢量部分,q是三维空间的一个向量。
2)复数式:Q=q0+q1i+q2j+q3k,它的共轭复数:Q*=q0−q1i−q2j−q3k。
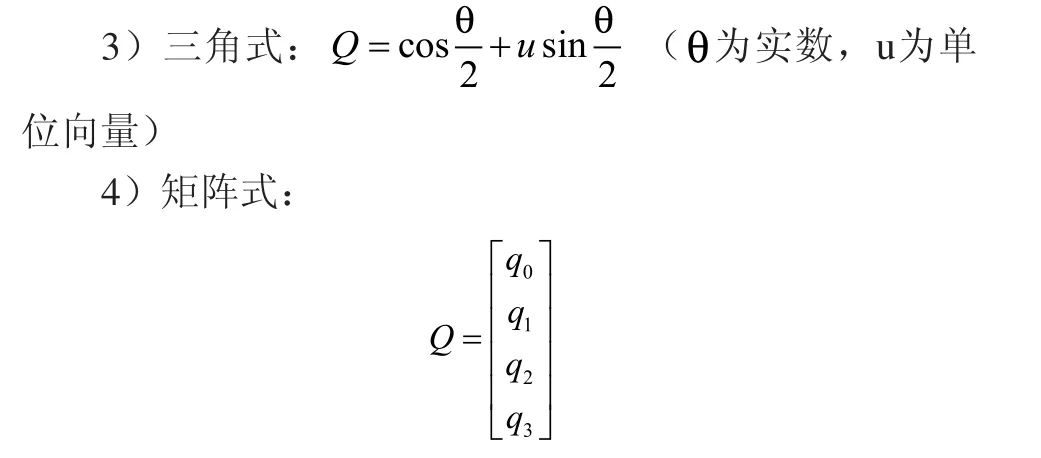
2.2 四元数的矢量变换
四元数算法的基本原理是:一个坐标系变换到另一个坐标系,可以通过绕一个定义在参考坐标系中的矢量u的单次转动来实现[5]。在载体系定义一个矢量rb=xi+yi+zk,设其在参考系中表示为rn。则有rn=qrbq*,其中q=a+bi+cj+dk,q*为共轭复数。

将其写成矩阵形式:
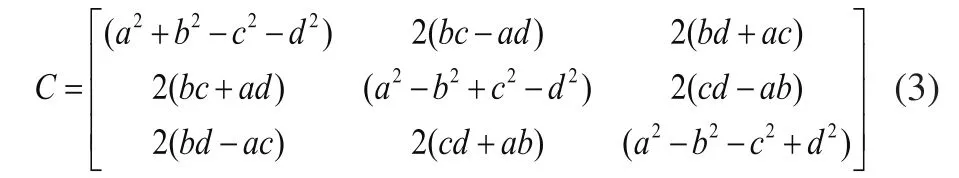
这个矩阵就是四元数旋转矩阵。
用欧拉角直接表示四元数:

2.3 四元数姿态解算
我们开始可以随便假设一个四元数,且认为它表征了两个坐标系之间的旋转关系了,只不过这个旋转矩阵跟真实的矩阵相比误差很大,我们假设这个矩阵是正确的,然后得到两个坐标下同一个向量的差别,用这个差别来纠正这个矩阵。也就是说我们只知道重力在地理坐标系下向量是(0,0,g),如果我们的矩阵是准确的,那么用这个矩阵将(0,0,g)转换到机体坐标,那我们应该得到在机体坐标系下的重力的向量,如果矩阵很准确,那我们从加速度计读取的数值应该也是这个向量,所以我们读取加速度计得到重力向量在机体坐标系下的向量,这是测量值,这个值和理论值有差别,用这个差别来纠正旋转矩阵[6]。
1)将机体坐标系的电子罗盘测到的矢量转成地理坐标系下的磁场矢量hxyz(测量值)然后令其在Y方向为0、X方向大小等于磁场矢量在hxy平面上的投影。得到标定后的矢量bxyz。

2)将地理坐标系的标准重力向量(0,0,g)及标定以后的磁场矢量分别左乘上四元素旋转矩阵,转到机体坐标系。

3)将加速度计测出来的重力向量和参考矢量做叉积,磁场的测量矢量和参考矢量也做叉积,都用来修正陀螺仪。

4)由于叉积向量大小与陀螺积分误差成正比,因此在误差上乘上一个系数去修正陀螺仪数据。
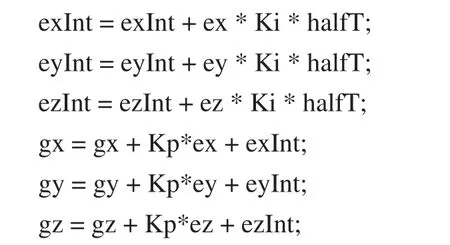
5)计算四元数的微分方程、并进行归一化处理:四元数微分方程本来只是基于角速度的,也就是说,已知上个周期的姿态,和本次测量得到的角速度,得到本周期的姿态,在角速度里加入误差反馈,来调节姿态,起到减小误差的作用。


6)最后将四元数转化成欧拉角进行表示。
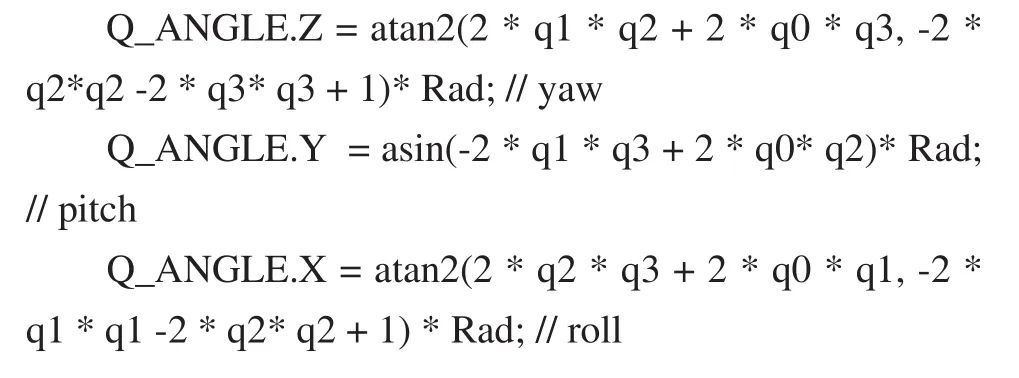
2.4 实验结果
实验采集到650组数据,并利用MATLAB对数据进行了处理,结果如图3和图4所示。

图3 分别为加速度X(g)、Y(g)、Z(g)曲线
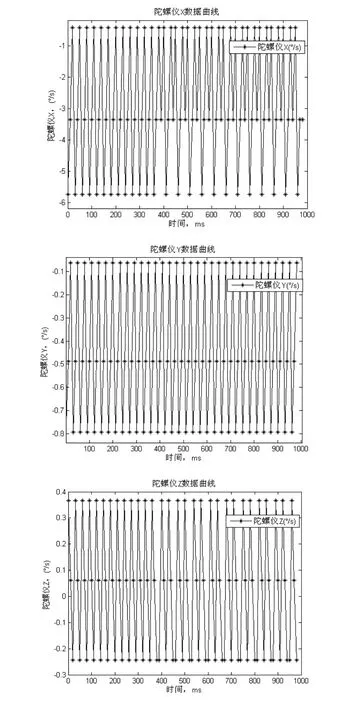
图4 陀螺仪X、Y、Z轴(°/s)曲线

图5 四元数曲线
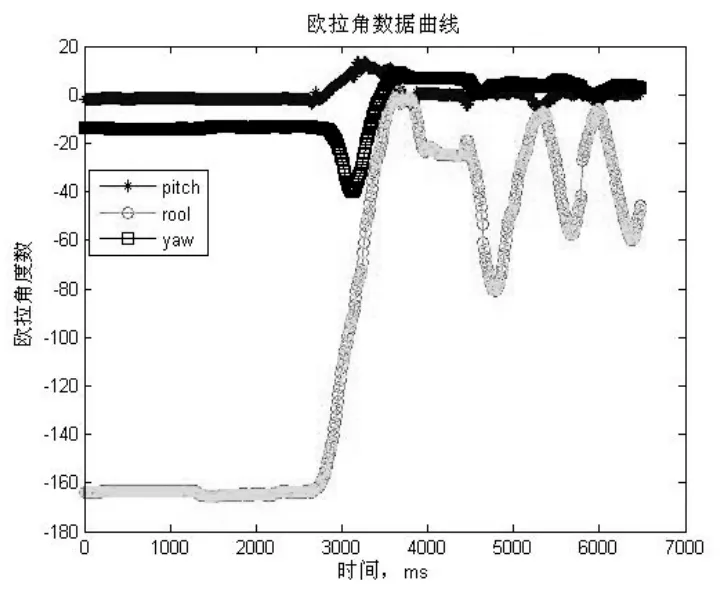
图6 欧拉角曲线
3 结论
本文在基于欧拉角、四元数微分方程的基础上,用四元数把三轴陀螺仪以及加速度计的数据进行融合,并且经过实验证明了四元数算法的有效性,从而说明四元数算法在飞行器姿态控制方面有着很好的应用前景。
[1]White K C, Tunnell P J. A Guidance Scheme for Lunar Desent Based on Linear Perturbation Theory[R].NASA TN D-3147.1965,1-20.
[2]程国采.弹道导弹制导方法与最优控制[M].长沙:国防科技大学出版社,1987
[3]陈印.GridView中数据行批量删除的实现[J].四川职业技术学院学报,2014,24(1).
[4]Be lbruno E A. Luna rCapture Orb its, A M e thod o fC onstructing Ea rth M oon Tra jectories and the Lunar Gas M ission[C].A IAA-87-1054. In:19th A IAA /DGLR /JSASS Interna tiona l E lec tric Propulsion Confe rence. Co lo rado Sp ring s, Co lo rado, M ay,1987.
[5]Serban R,KoonW S, Lo M W etc.,H alo O rbitM ission Correction M aneuvers Using Op tim a l Contro l[J].Automa tica,2002,38:571-583.
[6]杨嘉墀,范剑峰,尚秉民,等.航天器轨道动力学与控制(上)[M].北京:宇航出版社,1995,547-549.
Attitude solution algorithm for four rotor aircraft based on four element number
JIANG Yu1, CHEN Hai-yun2, CEN Ru-ping3
由于四旋翼飞行器参与了许多极具挑战性的任务,因此要求飞行器在飞行时具有很好的飞行姿态,姿态控制问题就成了当前研究热点。详细分析了欧拉角算法和时效性更好的四元数算法,最后通过实验验证了该算法的有效性。
四旋翼飞行器;欧拉角;四元数;姿态解算
蒋钰(1990 -),女,广西人,硕士研究生,主要从事自动化方面的研究工作。
TP13
A
1009-0134(2015)12(上)-0077-04
10.3969/j.issn.1009-0134.2015.23.22
2015-07-23
国家级大学生创新创业训练计划项目(201410615002)
