多元正态向量变点在线监测

刘维奇，刘晋芳，秦瑞兵

（1.山西大学 管理与决策研究所，山西 太原 030006；2.山西大学 数学科学学院，山西 太原 030006）

0 引言

在质量工程控制中，需要对生产线上的产品进行抽检以检验产品质量是否合格，特别是要检验产品的质量是否发生显著波动或超出其质量控制范围，从而当产品的质量发生突变时能及时报警，避免出现更多的次品。出现质变的时刻称为变点。在实际应用中，数据的生成机制常由于内在或外在因素的变化而发生变化。因此很多实际数据存在变点，而对变点的统计推断可以使数据的统计分析更为准确，因此变点从质量控制领域逐渐应用到经济、金融、医学、气候分析等诸多领域。变点问题最初由Page［1］提出，由于其理论和应用的重要性而受到很多统计学者的关注。Bai［2］基于最小二乘法给出了线性过程均值变点的估计。Bai［3］用极大似然法考虑回归模型系数的多变点问题。Perron 基于最小二乘法考虑了对参数有约束的线性回归模型的多变点问题。近年来，多元时间序列的变点问题也逐渐受到统计学者的关注。Horváth［5］提出了监测多元相依稳定过程均值变点的几个统计量。Boutahar［6］提出了一个检验多元时间序列的非参数CUSUM方法。关于变点的其他文献，参考 Csörgö和 Horváth［7］，Perron［8］。

变点问题可以分为两类：一类是后验检验，即在给定的一组固定样本中检测是否有变点发生；一类是在线监测，即在已有模型的基础上对新观测的数据监测，直到出现变点才停止。在实际应用中对金融数据的监测更多采用实时监测。此即Chu［9］提出的在线监测问题。Carsoule和Franses［10］基于极大似然法对欧洲名义汇率波动的方差变点进行监测。Andreou等［11］和Zeileisd等［12］用最小二乘法考虑了动态经济模型中的变点监测问题。Horváth等［13］提出了分别基于残差累积和与递归残差累积和的统计量监测线性回归模型中变点的两种监测方案。其模拟结果表明，该方法能够较快地监测到较早发生的变点，而对于离开始位置较远的变点其监测的平均运行长度较长。陈占寿［14］通过引入窗宽参数改变监测的开始时刻对文献［13］中方法进行改进，这样当变点出现的时刻离最初监测的位置较远时，可以通过滑动监测的开始时刻使得变点看起来较早发生。陈占寿［15］用滑动核加权比率统计量监测带有趋势项时间序列的持久性变点。

针对多元时间序列均值变点问题，本文采用陈占寿［14］引进窗宽参数的方法，构造带有窗宽参数的残差累积和统计量监测多元正态向量均值变点。模拟表明引入窗宽参数可以改变监测开始的时刻，从而将较晚出现的变点移动到较早的时刻以增大检验的势，同时能减小平均运行长度，达到快速监测变点的目的。

1 模型

我们考虑下列模型：其中Xi是一个d×1维正态随机向量，μi是一个d×1维向量，ei是d×1维残差序列，满足下面假设条件：

假设1：误差序列满足：

（1）｛ei，i＝1，2，…，n｝独立同分布，且有E ei，j＝0，（1≤i＜∞，1≤j≤d）和E‖ei‖ν＜∞，ν＞2.

（2）存在正整数m，使得对任意的k和l，若1－k＞m，则有σ｛ei，1≤i＜k｝和σ｛ei，l≤i＜∞｝相互独立。

假设2：｛μi，i＝1，2，…，n｝和｛ei，i＝1，2，…，n｝相互独立。

假设3：存在一d维矩阵D使得

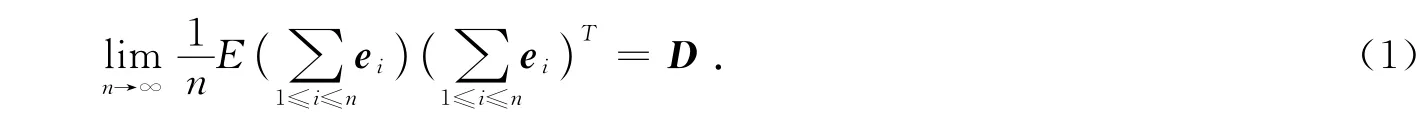
假设4：向量Xi的各分量彼此独立，记

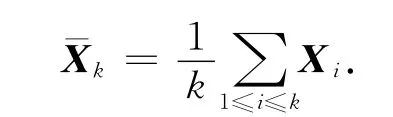
假设5：前m个历史样本是无污染的，即

以上假设1－3是证明监测统计量的渐近性质的必要条件，与Horváth［13］中的假设相同。

现在基于前m个样本观测值，从第m＋1个观测值开始监测，即检验原假设（H0）

和备择假设（H1）

其中向量μ0，μ1和k＊≥1均未知。

2 监测方法和主要结果

我们构造的残差CUSUM统计量如下：

3 模拟计算和实例分析

3.1 模拟计算

这部分通过蒙特卡罗模拟方法检验本文方法有限样本下的性质。因为在模拟中矩阵D是未知参数矩阵，需要估计。由Horváth［5］中结果知，可用基于前m个样本观测值的Dm估计，其中

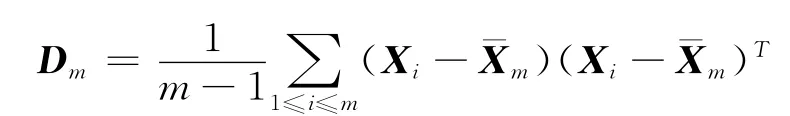
且满足：‖Dm－D‖＝oP（（log logm）－1／2）.可以证明前面的定理在Dm下依然成立。

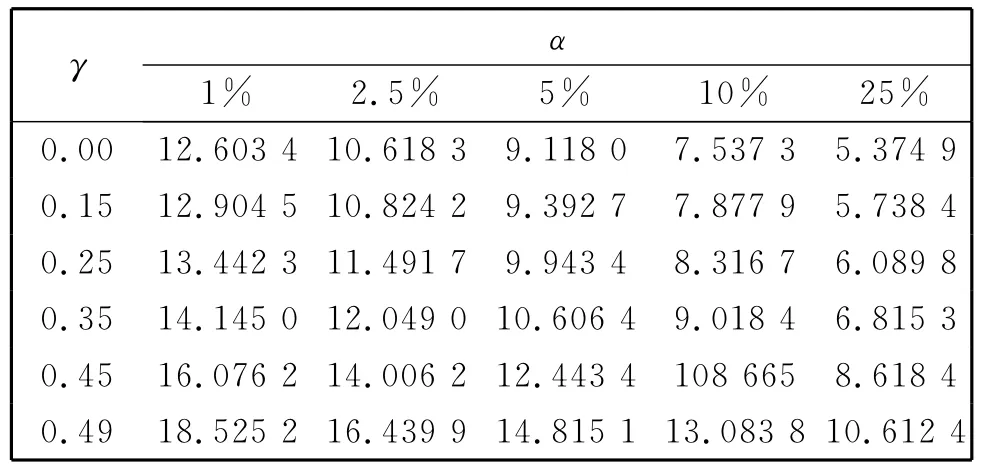
表1 临界值表Table 1 Critical values

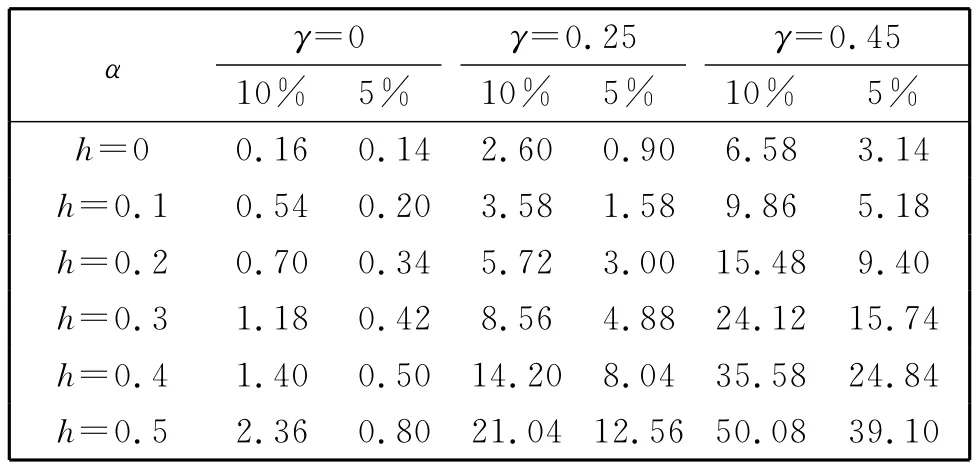
表2 监测样本量q＝2 m时的经验水平Table 2 Empirical size when q＝2m

表1列出了当d＝3时，基于的50 000次模拟得到的临界值。表2是样本量m＝200，监测长度q＝2m时的经验水平。从表中得知，随着h的增大，经验水平越来越大，也就是说h越大监测统计量越灵敏。另外，当γ＝0.45，h≥0.2和γ＝0.25，h≥0.4时存在水平失真问题。而在其他情况下，随着γ和h的增大，经验水平逐渐靠近检验水平。

表3和表4是考虑均值向量从（0，0，0）′变化到（0.6，0.6，0.6）′时模拟得到的势，其中样本容量m＝50，100，200监测长度q＝m。从表中可得：随着样本量的增加，检验的势逐渐增大；在样本量和变点位置都相同的情况下，γ的增大会提高检验的势，同时减小平均运行长度；当变点位置靠前时，在样本量较大的时候，改变h的取值对检验的势和平均运行长度影响不大，甚至较大的h值会减小检验的势，同时平均运行长度会增加；而当变点的位置靠后时，引入窗宽参数会明显提升检验的势，且此时检验的平均运行长度明显减小，因此本文方法可以适用于变点位置靠后的情况。

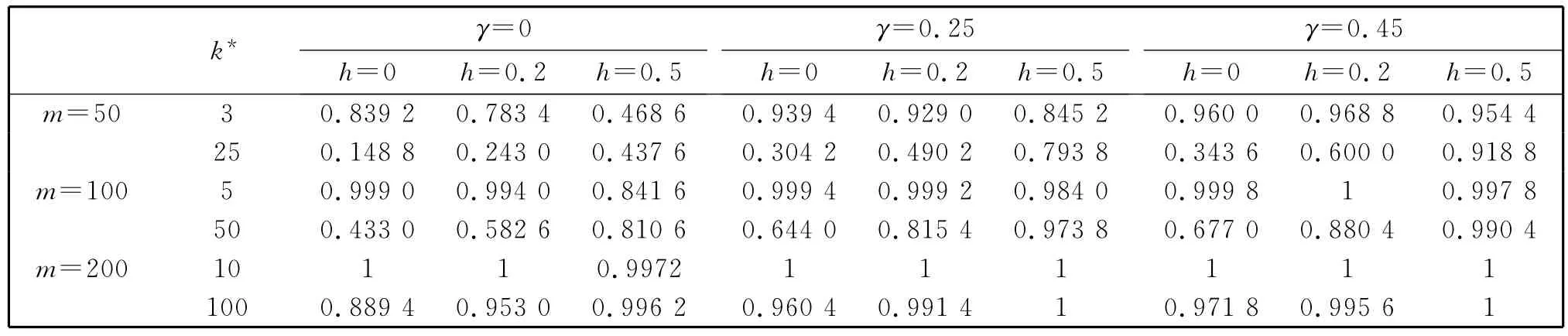
表3 检验的势（显著水平为5%）Table 3 Empirical power of the procedure

表4 检验的平均运行长度（显著水平为5%）Table 4 ARLs of the procedures

此外γ＝0.45，h＝0.2适用于监测不久就出现变点的情况，γ＝0.25，h＝0.5适用于变点较晚出现的情况。而在实际应用中，当我们不能确定变点的大致位置时，可以选择γ＝0.25，h＝0.2，以便达到两者的折中且尽可能快速地监测到变点。

3.2 实例分析

通过一个白酒的生产过程实例来说明本文方法的有效性。数据包括从2004年5月到2007年2月的4 898个观测，该数据集可以从UCI机器学习数据库（http ∥archive.ics.uci.edu ml datasets Wine＋Quality）中的“Wine Quality Data Set”中得到。此数据集中包括12个变量，分别是：非挥发性酸、挥发性酸度、柠檬酸、残留糖、氯化物、游离二氧化硫、总二氧化硫、密度、p H、硫酸盐和乙醇（分别记作y1，y2，y3，y4，y5，y6，y7，y8，y9，y10，y11）。还有一个由感官分析得到的质量分类变量，此分类变量的取值为0－10，取值为6时表示口感最好，取值越偏离6表示口感越差，取值为5－7都表示质量在可控范围之内。关于此数据集更多详细的信息可以参考Cortez［16］。

我们的目标是监测VinhoVerde白葡萄酒的生产过程以确保所生产酒的质量（口感）合格。为了方便，在这里我们只对前1 000个数据做分析，选取三个分量，分别是：非挥发性酸（y1）、总二氧化硫（y7）、密度（y9）。图1是这三个变量的原始数据图，图2的Q-Q图表明这三个变量分别都服从正态分布，通过计算相关系数矩阵得知此三个变量是不相关的。图3的三元Q-Q图表明该数据服从多元正态分布。因此，我们所选用的数据集符合前文中提出的假设。

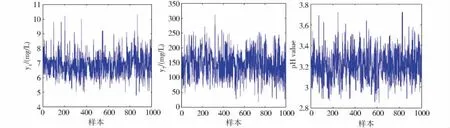
Fig.1 Raw data of y1，y7 and y 9图1 变量y 1、y 7和y 9的原始数据散点图

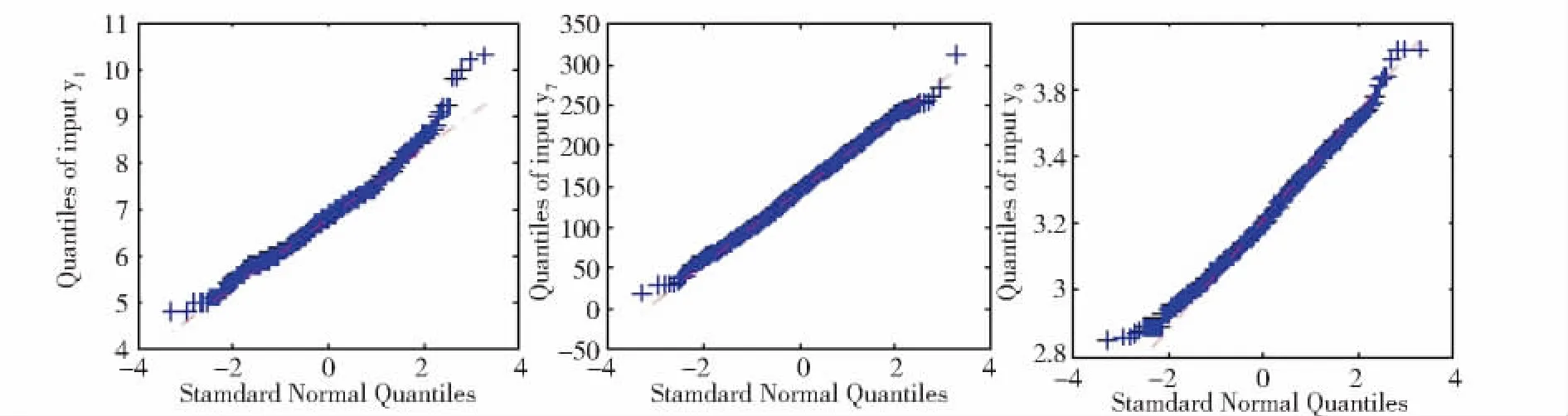
Fig.2 Q-Q plot of y 1，y 7 and y 9图2 变量y 1、y 7和y 9的Q-Q图

Fig.3 Q-Q plot of y 1，y 7 and y 9图3 变量的三元Q-Q图

下面开始对该数据集做变点监测。如图1所示，前150个数据各分量均值中不存在明显的变化，因此选取前150个数据作为历史样本。我们把监测到的变点位置标注到质量分类变量的散点图中，如图4所示，令γ＝0.25，h＝0，在5%的显著性水平下从第151个样本（图4中红虚线的位置）开始监测。在k＝187的位置（图4中红实线的位置）监测到变点。若选取γ＝0.25，h＝0.25，则在k＝154的位置（图4中绿实线的位置）监测到变点，该结果表明采用引入窗宽参数的方法确实能够更早的监测到变点。

4 结论与展望

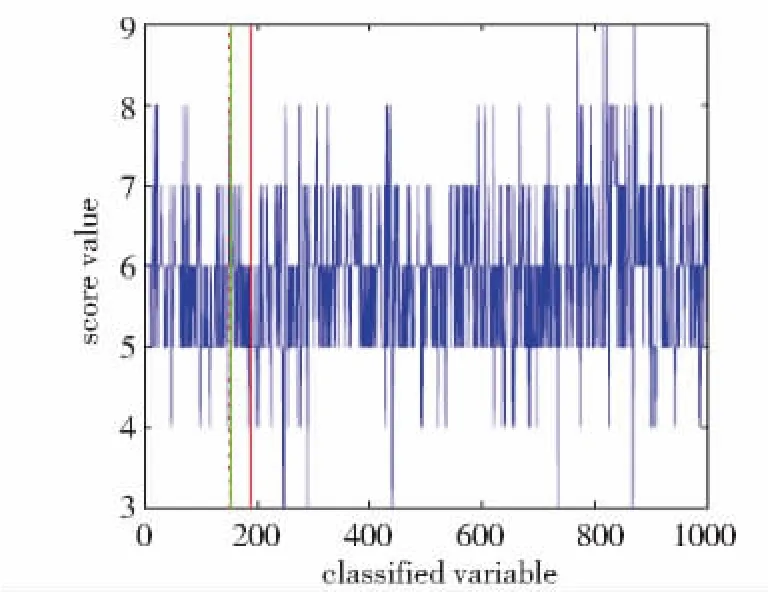
Fig.4 Q-Q plot of y 1、y 7 and y 9图4 监测结果图

对于存在变点的多元时间序列，如何较早的监测到变点，对控制风险做出有效决策具有现实意义。本文通过采用引入窗宽参数法，使得多元时间序列均值变点靠后时能尽快监测到变点。模拟表明窗宽参数选取合理可以使检验的误报率减小，同时使得平均运行长度减小。另外，本文考虑的是分量之间独立的变点监测，对于分量相依的情形还有待后续研究。

［1］ Page E S.A Test for a Change in a Parameter Occurring at an Unknown Point［J］.Biometrika，1955，42（3）：523-527.

［2］ Bai J.Least Squares Estimation of a Shift in Linear Processes［J］.Journal of Time Series Analysis，1994，15（5）：453-472.

［3］ Bai J.Likelihood Ratio Tests for Multiple Structural Changes［J］.Journal of Econometrics，1999，91（2）：299-323.

［4］ Perron P，Qu Z.Estimating Restricted Structural Change Models［J］.Journal of Econometrics，2006，134（2）：373-399.

［5］ Horváth L，Kokoszka P，Steinebach J.Testing for Changes in Multivariate Dependent Observations with an Application to Temperature Changes［J］.Journal of Multivariate Analysis，1999，68（1）：96-119.

［6］ Boutahar M.Testing for Change in Mean of Independent Multivariate Observations with Time Varying Covariance［J］.Journal of Probability and Statistics，2012，2012：1-17.

［7］ CsörgöM，Horváth L.Limit Theorems in Change-Point Analysis［M］.New York：John Wiley ＆ Sons，1997.

［8］ Perron P.Dealing with Structural Breaks［M］.Palgrave Handbook of Econometrics Vol 1，New York：Palgrave Macmillan，2006：278-352.

［9］ Chu C S J，Stinchcombe M，White H.Monitoring Structural Change［J］.Econometrica，1996，64（5）：1045-1063.

［10］ Carsoule F，Franses P H.Monitoring Structural Change in Variance，with an Application to European Nomianl Exchange Rate Volatility［J］.Econometric，1999，6：1-33.

［11］ Andreou E，Ghysels E.Monitoring Disruptions in Finacial Markets［J］.Journal of Econometrics，2006，135（1）：77-124.

［12］ Zeileis A，Leisch F，Kleiber C，et al.Monitoring Structural Change in Dynamic Econometric Models［J］.Journal of Applied Econometrics，2005，20（1）：99-121.

［13］ Horváth L，HuškováM，Kokoszka P，et al.Monitoring Changes in Linear Models［J］.Journal of Statistical Planning and Inference，2004，126（1）：225-251.

［14］ 陈占寿，田铮，丁明涛.线性回归模型参数变点的在线监测［J］.系统工程理论与实践，2010，30（6）：1047-1054.

［15］ 陈占寿，田铮.含趋势项时间序列持久性变点监测［J］.系统工程理论与实践，2014，34（4）：936-943.

［16］ Cortez P，Cerdeira A，Almeida F，et al.Modeling Wine Preferences by Data Mining from Physicochemical Properties［J］.Decision Support Systems，2009，47（4）：547-533.