大数据下的PAC－Bayesian学习理论综述

杨雪冰，张文生，杨阳

（中国科学院 自动化研究所，北京 100190）

0 引言

随着产业技术的飞速发展，大数据覆盖行业越来越广，人们逐渐认识到海量数据中蕴涵巨额经济价值与社会效益。如何有效地分析数据结构，建立数据之间的联系和挖掘数据的内在价值是当前人工智能领域的研究热点。机器学习是人工智能的核心研究方法，然而大数据的产生呈现价值稀疏、规模巨大、高维异构、实时非确定、关系复杂等特点，使得传统的机器学习方法无法直接用于大数据处理与分析。目前已有诸多经典的机器学习方法经过优化与调整应用于大数据，同时也有很多新的针对大数据的思路和方法提出，然而，对大数据的分析与处理仍然处在探索阶段，至今未有统一的适合于大数据的理论框架与系统应用。

按照计算学习理论（computational learning theory）［1］的观点，概念的可学习性是利用机器学习方法挖掘数据内在价值时首先要考虑的。对于海量数据下的问题，通过在理论上对其是否可学习做出判断，可以显著降低分析与处理的代价。然而，传统意义的可学习理论（PAC learnable）在大数据学习中存在着很多局限性，自提出以来经诸多学者进行了发展与推广，其中效果最好、应用最广并且在当今仍有后续研究的便是PAC－Bayesian学习理论。该理论将可学习理论与贝叶斯学习高度结合，为已有算法提供其泛化误差界的证明以指导算法改进或验证算法是否适合某些具体问题。PAC－Bayesian学习理论给出的界不依赖样本分布以及先验的正确性，同时给出足够紧（甚至是最紧）的泛化误差界，因此在理论与应用层面均具有很大的研究价值。

汤莉等人在PAC－Bayesian边界计算［2－3］方面做了很多突出的工作，且在文献［4］中从介绍PAC－Bayesian边界在SVM中的应用出发，详细而全面地综述了PAC－Bayesian边界在众多机器学习算法中的应用并指出该理论未来的研究方向，但是并未介绍PAC－Bayesian定理最基本的形式以及最一般的形式，也没有对PAC的核心概念样本复杂度进行深入考虑，故而没有揭示该理论得以广泛应用的根本原因。本文旨在从PAC的角度来理解PAC－Bayesian学习理论的核心内容，并探讨该理论在大数据环境下得以广泛应用的可能。

基于上述考虑，本文首先介绍PAC可学习理论的基本思想，而后简要介绍贝叶斯学习，进而从分析二者的优势与局限出发，揭示PAC－Bayesian学习理论的产生背景与本质内涵，最后着眼于大数据理论与应用，分析PAC－Bayesian适合于大数据的原因以及该理论在大数据环境下的研究现状和未来的研究方向。

1 PAC可学习理论的基本思想

概率近似正确理论（probably approximately correct，PAC），又称可学习（learnable）理论，由 Valiant于1984年首次提出［5］，而后在计算学习、统计机器学习、人工智能、人工神经元网络、模式识别等领域得到广泛研究［1］。PAC是一种基于统计的学习理论，其思想与VC维（Vpanik－Chervonenkis dimension）的思想有很多相近之处［6－8］。PAC可学习理论的核心是首先将模型的泛化误差ε与置信水平δ作为评价一个学习模型性能好坏的参数，而后在给定这两个参数之后，得到一个所需训练样本个数的理论下界，这个理论下界便是PAC可学习理论中的关键概念，即样本复杂度（sample complexity）。下面对该理论的基本思想作一个简要的介绍。

PAC是一种基于样本的概念学习（concept learning）理论。给定一个空间X∈R，待研究的概念空间C是该空间的子空间，C⊆X，我们通过学习算法得到的假设构成的空间也是X的子空间，H⊆X，需要说明的是，H与C可能相等也可能不等（往往是不相等的）。一般地，我们只关心概念空间中的某一个概念c，并希望通过有限数量的样本来“尽可能近似地”学习到此概念，即在某种确定的度量下，学习算法输出的假设h和c是足够接近的。如果用泛化误差ε来描述所得假设h与目标概念c的差异是否“近似”，用置信水平δ来表征上述结果是否“尽可能”，我们称一个算法对概念空间C是PAC的当且仅当对于较小的ε，δ，对任意概念空间中的概念c和任意概率分布Pμ，满足

我们称使得上述公式成立最小训练样本数为样本复杂度m0。换句话说，当算法的输入样本数大于m0时，算法可以在概率意义上完成对目标概念足够近似正确地学习［9］。

为了更直观说明PAC的基本思想，这里介绍一个经典的例子［6］，如图1所示。

Fig.1 Learning concept of“medium build”图1 学习概念“中等身材”

解释：对成年男子而言，认为身高在1.63～1.83m之间，体重在68～84kg之间为中等身材，随机选择有限数量的样本进行训练，即输入带标签［＋，－］的样本［体重，身高］进行学习，得到的最优假设是以正样本为边界点的最大矩形。

通过这个例子，可以容易地发现随着训练样本增多，代表最优假设的矩形越有可能更好地逼近代表目标概念的矩形。在给定δ下，若算法是PAC的，样本数量（m）与逼近程度（泛化误差）在假设空间的势｜H｜有限时关系如下［9］：

式（2）说明欲达到给定的泛化误差与置信水平要求并且确保算法是PAC的，只需要保证假设空间的势有限并且训练样本数量大于样本复杂度，该式中所得的下界与遗传算法中的初始种群规模（population size）类似，文献［10］指出PAC理论得到的样本复杂度可有效地用于指导遗传算法选择初始种群规模，说明了样本复杂度的实际应用价值。

与式（2）等价的描述为：

式（3）说明，PAC理论的最大优点在于给定训练样本数量，如果能够证明算法是PAC的，则说明算法的效果有一个不依赖于目标概念（即目标概念可以在概念空间随机选择）且不依赖于训练样本分布与选择方式的理论上界，Vapnik在文献［11］中介绍了关于这个理论上界的更多内容并且扩展到对假设空间的势｜H｜无限时算法PAC性质的讨论。

2 贝叶斯学习

Mitchell在文献［12］中系统介绍了贝叶斯方法在机器学习中的理论与应用，这里我们从一个二分问题出发简要地对贝叶斯学习框架进行介绍，主要考虑两类分类器，贝叶斯最优分类器与吉布斯分类器。

假定训练样本集S＝｛（x1，y1），…，（xm，ym）｜xi∈X⊂Rn，yi∈Y＝｛－1，＋1｝｝⊂X×Y，在PAC学习模型假设下，每一个带标签的样本（xi，yi）依固定但未知的分布D从X×Y中随机选择。假设空间H中的每一个假设均可以看作一个分类器，即h∶X→Y。从统计角度，对真实误差和经验误差定义如下（这里统一采用文献［13］中的符号记法）：

其中，I（a）为1若a为真，I（a）为0若a为假。

贝叶斯学习规则是根据训练样本，确定假设空间中的假设（分类器）h所服从的后验分布Q，而后根据此分布赋予每一个假设相应的权重，最后以一个加权投票的方式得到分类器BQ，即：

可见，贝叶斯学习的关键是假定假设空间的先验分布，利用观测数据得到的似然，确定假设空间的后验分布，在对新来的样本进行分类时依据得到的后验分布利用多个假设通过加权使得经验风险最小，这种学习算法得到的分类器称为贝叶斯最优分类器，属于加权投票算法的特例［14－15］，能够从给定训练数据中获得最好的性能［16］。

但是，由于贝叶斯最优分类器算法开销大并且可能得到不属于假设空间中的假设，因此人们设计了另外一种常用的近似最优分类器来替代，即吉布斯分类器。该分类器在得到Q之后不采用加权处理，而是通过采样的方式依概率分布Q随机地选择一个分类器h。类似地，可以定义吉布斯分类器的真实误差和经验误差：

理论上［17］已严格证明贝叶斯最优分类器的泛化误差R（BQ）最多为吉布斯分类器泛化误差的2倍（这一点从二分问题可以很直观地得出），即：

依据此公式，研究者在分析贝叶斯最优分类器的泛化误差上界时往往转化为分析相应的吉布斯分类器的泛化误差上界。

3 PAC－Bayesian理论

前面已经论述了PAC的泛化误差界在假设空间有限时很容易得出并且是一个较紧的界，现在考虑一种更为一般的情况，考虑概念空间是一个元素可数无穷多的集合，其VC维是无限的［15］，这时便无法直接使用一般的PAC理论来给出泛化误差的界，而若采用VC维的理论，给出泛化误差界太松。另一方面，传统的贝叶斯方法对先验知识过于依赖，以至于先验分布不正确时，模型的泛化误差难以控制。可见传统的PAC理论与贝叶斯学习有其固有的缺点。

从另一个角度，注意到PAC理论的优势在于给定置信水平与训练样本数目（这里关注泛化误差，换个角度可同样关注样本复杂度）之后，不依赖于模型的先验对错，也不依赖于由训练数据得到的后验分布，均能够给出模型的泛化误差界；贝叶斯学习的优势在于不同程度地利用领域知识作为先验（虽然承受先验可能不正确的风险），并且以先验和后验的概念来描述概念空间和假设空间的性质，描述了一种统计意义的“平均”情况而不局限于分析假设空间的势或者概念空间的VC维。可见，PAC理论与贝叶斯学习是优劣互补的，因此PAC－Bayesian理论的出发点与精髓之处在于考虑假设空间先验分布，但不限制该分布的正确性，给出模型一个泛化误差上界。而后根据这个上界，可以进行可学习性的证明，模型选择与评价以及基于这个界进行度量学习与相关优化算法的改进。

基于上述考虑，1997年Shawe－Taylor首次将PAC理论用于贝叶斯学习［17］，形成了最早的PAC－Bayesian思想。1998年，McAllester在计算学习领域著名会议COLT发文，正式以定理的形式提出PAC－Bayesian学习理论［18］，此后他对提出的PAC－Bayesian泛化误差界进行了改善，开始尝试应用于随机模型选择和模型均化［19－20］，后续也有学者Seeger［21］，Langford［22］，Catoni［23］陆续提出更紧的界。在2009年，Germain以定理形式推导出一个最为一般的PAC－Bayesian泛化误差界，证明了前人各种形式的界均可以作为此定理的推论［13］。此后在PAC－Bayesian理论研究层面基本没有重大的实质性进展。近年来在理论层面的研究主要集中于对某些情况下更紧边界的分析和推导等［25－26］。另一方面，该理论在应用层面不止局限于最初提到的模型选择、线性分类器、SVM等方向，而越来越多地出现于各类机器学习领域，如领域适应［27－28］与直推学习［29－30］等，详见文献［4］，本文在这一点上不再赘述。

这里为了方便理解前面提到的PAC－Bayesian理论本质，介绍最早的和最一般的PAC定理。

（McAllester（1998）定理1）若由概念空间C中的概念c得到的样本服从任意分布D，对任意先验分布为P的假设空间H，任意给定概念空间和样本空间的测度，对任意δ∈（0，1］，对任意假设空间的H的子空间U，有：

其中错误率ε（U）＝Ec∈Uε（c）实质上就是学习到的后验分布为Q的假设（子）空间的泛化误差。同时，通过这个定理，结合贝叶斯学习规则，可以发现这个泛化误差界同时体现出先验分布P的影响，进而可以通过优化先验分布来使得该泛化误差界更紧，即获得更小的分类误差。研究表明［24］，相比于其他理论，PAC－Bayesian学习理论得到的泛化误差界更紧，因此在式（10）基础上对界做进一步优化成了后续研究热点。

（Germain（2009）定理2.1）若由概念空间C中的概念c得到的样本服从任意分布D，对任意先验分布为P 的假设空间H，对任意δ∈（0，1］以及任意凸函数Ψ：［0，1］×［0，1］→R，有：

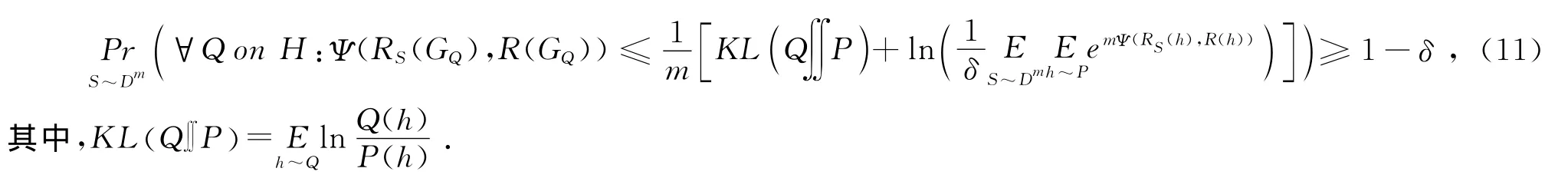
这个定理对之前研究者得到的PAC－Bayesian泛化误差界的高度概括之处体现在用一个凸函数来表示一切形式的“误差”，当该函数取不同形式时，可以得到不同的界，因此PAC－Bayesian与传统机器学习或优化算法结合的核心思路就是选择特定的凸函数Ψ并对式（11）得到的泛化误差界进行优化。

4 大数据与PAC－Bayesian

传统的PAC理论虽然旨在描述概念空间是否可学习，但在诸多实际问题中的应用碰到了种种困难，至少有两方面的原因，一方面是之前已提到的假设空间的势为无限的情况，不易直接应用PAC理论；另一方面是与PAC有关的各种理论（包括PAC－Bayesian）表明在实际问题中，若欲将算法的泛化误差控制在一个较低的水平则得到的样本复杂度往往特别大（如文献［24］中，106量级），导致难以进行实验验证。但是在大数据的时代，样本数量已不是问题，PAC理论的局限性在一定意义上有所减弱，另外PAC－Bayesian学习理论的深入发展进一步给可学习理论带来了新的血液。大数据的4V特性（体量大（volume）、异构（variety）、低价值密度（value）、实时（velocity））［31］决定了大数据时代的机器学习问题与传统的机器学习问题有很大不同，给相关研究工作带来新的挑战。在这样的环境下，待求解的问题所对应的样本复杂度容易被满足，使得判断问题的可学习性成为可能，在海量的问题中，一旦被判断为不可学习便可节约大量的后续工作。另外，在问题的求解过程中为了提升性能、降低训练时间，往往会不同程度地利用先验知识，但是由于大数据下的问题的复杂性，人们在设计算法时希望考虑领域先验知识但同时面临所采用的先验知识可能不正确的风险。而PAC－Bayesian学习理论可以很好地解决这个问题。因此，PAC－Bayesian学习理论非常适合于大数据相关的理论分析，有着无限的应用潜力。

在已提出的PAC－Bayesian应用中，已有相当一部分适合于大数据环境的算法。例如Amini等在文献［32］中对提出的半监督学习算法给出PAC－Bayesian界，通过对只有少部分带标签的训练样本进行估计来得到风险边界，其算法可有效处理价值密度低的大规模数据；Germain等在文献［33］中提出一种基于PACBayesian泛化误差界的样本压缩方法，以先验分布和后验分布的KL散度为度量，旨在选择出有代表性的样本形成原样本空间的一个子集，适合于处理具有体量大特点的大数据；Morvant等在文献［34］中结合PACBayesian理论提出MinCq算法用于多媒体信息融合，虽然本质上仍采用投票的思想，但充分利用了投票的多样性，使其可用于处理异构数据；Keshet等在文献［35］中首次采用随机梯度下降即在线学习的方法来解PAC－Bayesian边界的优化问题，进而用于处理语音信号中的音素识别问题，表明该方法可用于处理实时数据。如Gheyas等在文献［36］中所说，算法结合能够较好弥补算法相互间的不足，由于大数据具有众多难解的特性，基于PAC－Bayesian理论的多方法融合必将是未来的趋势。

此外，值得注意的是，现有的适合于处理大数据问题的算法中，还有大量的热门算法没有相应的PACBayesian分析，如采用概率图模型［37］用于语音识别与社交网络分析，基于随机森林的Co－forest［38］用于辅助诊断中的分类问题等等，这类算法的共性是均要考虑先验知识，并且尚未得到相应的PAC－Bayesian泛化误差界，因此算法泛化性能的提升空间还很大，这预示着PAC－Bayesian学习理论在未来的大数据环境下仍需进一步深入研究。

5 结束语

本文立足于PAC可学习理论的基本思想，结合贝叶斯学习的理论框架，分析了PAC－Bayesian学习理论的由来以及本质内涵，通过其最初与最一般的定理揭示了该理论如何将PAC与贝叶斯结合起来达到更易应用于相关算法分析的效果。在大数据的时代，PAC－Bayesian学习理论已经初步展现出大数据算法分析的优势并有可能在未来的研究中在理论与应用层面均得到进一步的推进。此外，并行计算用于大数据处理已引起学术界和产业界越来越多的关注，探讨PAC－Bayesian理论在各类并行算法上的应用也是一个非常有意义的研究方向。

［1］Kearns M J，Vazirani U V.An Introduction to Computational Learning Theory［M］.Cambridge.MA：MIT press，1994.

［2］Tang Li，Yu Hua，Gong Xiujun，et al.On the PAC－Bayes Bound Calculation Based on Reproducing Kernel Hilbert Space［J］.Applied Mathematics and Information Sciences，2013，7（2）：817－822.

［3］Tang Li，Zhao Zheng，Gong Xiujun.A Refined MCMC Sampling from RKHS for PAC－Bayes Bound Calculation［J］.Journal of Computers，2014，9（4）：930－937.

［4］汤莉，宫秀军，何丽.PAC－Bayes理论及应用研究综述［J］.计算机科学与探索，2015，9（1）：1－13.

［5］Valiant L G.A Theory of the Learnable［J］.Communications of the ACM，1984，27（11）：1134－1142.

［6］Blumer A，Ehrenfeucht A，Haussler D，et al.Learnability and the Vapnik－Chervonenkis Dimension［J］.Journal of the ACM （JACM），1989，36（4）：929－965.

［7］Pestov V.PAC Learnability Versus VC Dimension：a footnote to a basic result of statistical learning［C］∥Neural Networks（IJCNN），The 2011International Joint Conference on.IEEE，2011：1141－1145.

［8］Wesley Calvert.PAC Learning，VC Dimension，and the Arithmetic Hierarchy［Z／OL］.ArXiv Preprint ArXiv：1406.1111，2014.

［9］Anthony M，Biggs N.Computational Learning Theory for Artificial Neural Networks［J］.North－Holland Mathematical Library，1993，51：25－62.

［10］Hernández－Aguirre A，Buckles B P，Martánez－Alcántara A.The Probably Approximately Correct（PAC）Population Size of a Genetic Algorithm［C］∥Tools with Artificial Intelligence，2000.ICTAI 2000∥Proceedings of 12th IEEE International Conference on.IEEE，2000：199－202.

［11］Vapnik V N，Vapnik V.Statistical Learning Theory［M］.New York：Wiley，1998.

［12］Anderson J R.Machine Learning：An artificial intelligence approach［M］.Morgan Kaufmann，1986.

［13］Germain P，Lacasse A，Laviolette F，et al.PAC－Bayesian Learning of Linear Classifiers［C］∥Proceedings of the 26th Annual International Conference on Machine Learning.ACM，2009：353－360.

［14］Shawe－Taylor J，Langford J.PAC－Bayes ＆ Margins［J］.Advances in Neural Information Processing Systems，2003，15：439.

［15］Linial N，Mansour Y，Rivest R L.Results on Learnability and the Vapnik－Chervonenkis Dimension［J］.Information and Computation，1991，90（1）：33－49.

［16］Zoubin Ghahramani.Probabilistic Machine Learning and Artificial Intelligence［J］.Nature，2015，521：452－459.

［17］Shawe－Taylor J，Williamson R C.A PAC Analysis of a Bayesian Estimator［C］∥Proceedings of the tenth annual conference on Computational learning theory.ACM，1997：2－9.

［18］McAllester D A.Some Pac－bayesian Theorems［C］∥Proceedings of the Eleventh Annual Conference on Computational Learning theory.ACM，1998：230－234.

［19］McAllester D A.PAC－Bayesian Model Averaging［C］∥Proceedings of the Twelfth Annual Conference on Computational Learning theory.ACM，1999：164－170.

［20］McAllester D A.PAC－Bayesian Stochastic Model Selection［J］.Machine Learning，2003，51（1）：5－21.

［21］Seeger M.Pac－bayesian Generalisation Error Bounds for Gaussian Process Classification［J］.The Journal of Machine Learning Research，2003，3：233－269.

［22］Langford J.Tutorial on Practical Prediction Theory for Classification［J］.Journal of Machine Learning Research，2005，6（3）：273－306.

［23］Catoni O.PAC－Bayesian Supervised Classification：the Thermodynamics of Statistical Learning［Z／OL］.ArXiv preprint ArXiv：0712.0248，2007.

［24］Herbrich R，Graepel T.A PAC－Bayesian Margin Bound for Linear Classifiers［J］.Information Theory，IEEE Transactions on，2002，48（12）：3140－3150.

［25］Lever G，Laviolette F，Shawe－Taylor J.Tighter PAC－Bayes Bounds Through Distribution－dependent Priors［J］.Theoretical Computer Science，2013，473：4－28.

［26］Honorio J，Jaakkola T.Tight Bounds for the Expected Risk of Linear Classifiers and PAC－Bayes Finite－Sample Guarantees［C］∥Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics，2014：384－392.

［27］Pascal Germain，Amaury Habrard，et al.A PAC－Bayesian Approach for Domain Adaptation with Specialization to Linear Classifiers［C］∥Proceedings of the 30th International Conference on Machine Learning（ICML－13）.2013：738－746.

［28］Germain P，Habrard A，Laviolette F，et al.An Improvement to the Domain Adaptation Bound in a PAC－Bayesian context［Z／OL］.ArXiv Preprint ArXiv：1501.03002，2015.

［29］Bégin L，Germain P，Laviolette F，et al.PAC－Bayesian Theory for Transductive Learning［C］∥Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics.2014：105－113.

［30］Balsubramani A，Freund Y.PAC－Bayes with Minimax for Confidence－Rated Transduction［Z／OL］.ArXiv Preprint ArXiv：1501.03838，2015.

［31］陈康，向勇，喻超.大数据时代机器学习的新趋势［J］.电信科学，2013，28（12）：88－95.

［32］Amini M，Usunier N，Laviolette F.A Transductive Bound for the Voted Classifier with an Application to Semi－supervised Learning［C］∥Advances in Neural Information Processing Systems，2009：65－72.

［33］Germain P，Lacoste A，Marchand M，et al.A PAC－Bayes Sample－compression Approach to Kernel Methods［C］∥Proceedings of the 28th International Conference on Machine Learning（ICML－11）.2011：297－304.

［34］Morvant E，Habrard A，Ayache S.PAC－Bayesian Majority Vote for Late Classifier Fusion［Z／OL］.ArXiv Preprint ArXiv：1207.1019，2012.

［35］Keshet J，McAllester D，Hazan T.Pac－bayesian Approach for Minimization of Phoneme Error Rate［C］∥Acoustics，Speech and Signal Processing（ICASSP），2011IEEE International Conference on.IEEE，2011：2224－2227.

［36］Gheyas I A，Smith L S.Feature Subset Selection in Large Dimensionality Domains［J］.Pattern Recognition，2010，43（1）：5－13.

［37］Koller D，Friedman N.Probabilistic Graphical Models：Principles and Techniques［M］.Cambridge，MA：MIT Press，2009.

［38］Li M，Zhou Z H.Improve Computer－aided Diagnosis with Machine Learning Techniques Using Undiagnosed Samples［J］.Systems，Man and Cybernetics，Part A：Systems and Humans，IEEE Transactions on，2007，37（6）：1088－1098.