小波包和小波脊线相结合的解调方法在液压泵故障诊断中的应用

2015-05-10燕山大学河北省重型机械流体动力传输与控制重点实验室河北秦皇岛066004燕山大学先进锻压成形技术与科学教育部重点实验室河北秦皇岛066004

液压与气动 2015年4期

，， (1．燕山大学河北省重型机械流体动力传输与控制重点实验室，河北秦皇岛 066004；2．燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004)

引言

液压泵在异常运行工作状态下受外界因素和本身故障的干扰影响，其振动信号存在非平稳和非线性特征。针对信号的非平稳性特征，人们提出了多种解决问题的方法。目前，应用最多的几种方法包括：短时傅立叶变换、Hilbert-Huang变换、二次型时频分布和小波分析等[1]。而小波包方法[2,3]不仅具备小波分析方法中时频局部化能力强的优势，而且对高频频带进行了进一步的划分，与小波分析相比具有更高的频率分辨率。

机械设备的早期故障一般具有冲击持续时间短和能量频率发散的特点[4]。其振动分量直接落在正常频率范围内的能量远不及其他低频域的分量。因此，传统的振动分析技术不能对该类故障进行有效的诊断。早期故障的低频冲击激起的高频共振信号包含大量的有用信息，提取其中感兴趣的频带信息，并对其进行共振解调处理可获得相对于低频冲击放大和扩展的共振解调波，对该波形信号进行频谱分析可以对早期故障进行有效的特征提取和故障诊断。小波脊线法是一种有效的共振解调方法，它可以提取调制信号的幅值信息，反映出故障的特征频率[5]。

本研究融合小波包分解与小波脊线解调方法的优势，对液压泵故障的振动信号进行了分析和处理。首先对原始信号进行功率谱分析，明确故障振动信号反映出的能量集中的高频频段带宽；根据确定的带宽和信号分析频率设定小波包分解的层数，采用小波包分解的方法提取感兴趣的频段信息，并进行信号重构；对提取频带能量最大的特征信息进行小波脊线解调，通过解调后的时频谱分析故障的频率特征。利用该方法对液压泵的单柱塞滑靴磨损、斜盘磨损和中心弹簧故障三种故障状态的信号进行分析，结果表明提出的信号解调方法对液压泵的单柱塞滑靴磨损、斜盘磨损和中心弹簧失效三种故障振动信号的分析过程是有效的。

1 小波包理论

小波包分解可用递归式(1)来实现[6,7]：

(1)

小波包重构的递归式是：

(2)

小波包分解的实质是让信号通过hk和gk这对高、低通组合滤波器同时进行二抽一的采样，从而能够把信号逐层分解到不同的频段上。频段宽度▽f与分解层数j及采样频率fs满足如下关系式:

(3)

图1是小波分解和小波包分解过程差异的对比。可以看出，每层的滤波器子带都覆盖信号所占有的频率，只是各层的频率分辨率不同，组合而成的滤波器组其特性覆盖整个频带。

2 小波脊线解调法[8,9]

任意的单分量实信号s(t)均可表示为:

s(t)=A(t)cos(φ(t))

(4)

式中,A(t)≥0，可称作瞬时幅值，φ(t)∈[0,2π)，称作瞬时相位。

信号s(t)的解析信号可以定义为:

Zs(t)=(1+iH)s(t)=As(t)exp(iφs(t))

(5)

式中，H为信号的Hilbert变换。

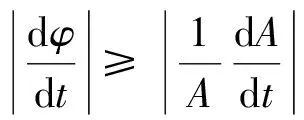
Zs(t)≈A(t)exp(iφs(t))

(6)

根据式(5)和式(6)可以定义渐进单分量信号s(t)的瞬时频率为：

(7)

显然，式(7)定义的瞬时频率能够更准确地描述频率随时间的变化，而傅里叶变换对此无能为力。

选择具有渐近性质的母小波ψ(t)，由式(5)可知，与之对应的解析小波为：

(8)

小波脊线是在相平面上满足ts(a,b)=b的所有点(a,b)的集合，即:

P={(a,b)∈R2;a>0,ts(a,b)=b}

(9)

小波脊线上的点(ar(b),b)称为小波脊点。即:

(10)

由小波脊线可以方便地得到信号的瞬时频率和瞬时幅值。通过将实对称窗函数g(t)乘以复正弦波exp(iω0(t))，可以构造出近似解析小波:

(11)

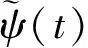
(12)

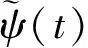
(13)

(14)

(16)

(17)

3 基于小波包分解和小波脊线的信号解调方法

故障诊断方法流程如图2所示。具体步骤如下：

(1) 对原始振动信号进行功率谱分析，明确故障振动信号反映出的能量集中频带带宽；

(2) 根据确定的带宽和信号分析频率，设定小波包分解的层数；

(3) 采用小波包能量法提取出能量最大的特征频带进行信号重构；

(4) 对重构后的频带信号进行小波脊线解调处理得到包络信号；

(5) 对包络信号进行低频段包络谱分析，提取故障的特征频率。

传播主体理论中的“自己人”效应理论指出若传播主体和传播受众来自同一国家或民族，传受双方在文化背景和价值观等方面相似，那么传播受众会更容易相信传播主体传递的信息（水淼 2009：86），传播效果会更佳。《天演论》的核心传播主体是严复，但还有一个重要人物也起到了传播主体的作用，即为《天演论》作序的桐城大家吴汝纶。严复和吴汝纶与作为目标传播受众的晚清封建士大夫有不少共同点：他们都是中国人，且在文学旨趣、文化背景、价值观等方面都有相似之处。在当时的士大夫眼里严复和吴汝纶是“自己人”。因此他们传播的信息更容易被目标传播受众接受。

图2 特征提取方法流程图

4 液压泵故障的实验分析

本实验是在材料实验机液压伺服系统试验平台上完成的，选取MCY14-1B型号轴向柱塞泵为研究对象，电机额定转速为1480 r/min。对泵壳的振动信号进行采集。人为设计轴向柱塞泵单柱塞滑靴磨损、斜盘磨损、中心弹簧失效和正常工作状态四种工作模式进行故障诊断分析。试验的主溢流阀压力调定为10 MPa，采样频率为50 kHz，每种故障的数据均截取时间为0.8 s的数据段作为原始信号。其试验台如图3所示。

4.1 功率谱分析

图3 液压泵故障诊断试验台

图4 液压泵各种状态的功率谱图

对液压泵故障的原始振动信号进行功率谱差值分析，如图4所示。从图4中可以看出，当发生三种故障时功率谱在3～5 kHz频段的谱线幅值整体有明显的增加，这说明液压泵在发生故障时向外传递的故障振动特征信号主要集中在这一频段。如果确定每3 kHz带宽作为一个频带，就能将故障信号的大部分高频部分特征信息容纳在一个频带内。

正常数据在大于3 kHz高频频带下没有明显的峰值变化，特征频率多集中在低频部分。而液压泵故障的功率谱图在3 kHz以上的高频部分有明显的峰值集中。由实验参数可知，信号的分析频率为25 kHz。由此，本研究将确定小波包分解层数为3层。从谱图中发现，故障信号高频部分峰值集中区域频率成分比较复杂，无法提取故障的特征频率。这是由于液压泵在发生损伤类故障时，损伤引起的冲击脉冲力，诱发液压泵结构的高频固有振动，而该高频振动的幅值受到冲击脉冲力的调制造成的。

4.2 小波包分解的特征频带提取

选择用Daubechies 5小波包进行信号分解，分解层数为3。在尺度3上形成了8个频带，每个分解系数对应的频带如表1所示。

表1 分解系数对应的频带

液压泵正常和故障信号经过小波包变换，各分解系数对应的频带能量比较如图5所示。由于早期故障冲击持续时间较短，其能量频率发散，落在液压泵正常频率范围内的分量十分微弱，无法与低频域中的其他振动分量相比，所以分解系数d30对应的低频域频带无法找到反映故障的有用特征信息。因此，对该频带将不做分析。本研究只对3125 Hz以上的高频部分能量进行比较。如图5所示。从图中可以看出，正常状态、单柱塞滑靴磨损、斜盘磨损以及中心弹簧失效故障的分解系数d31对应的频带能量值最高。因此，本研究提取该分解系数对应的频带进行信号重构，重构后振动信号的时域波形如图6所示。从重构后的时域波形图的比较可以发现，故障信号的幅值相对于正常信号有明显的增加，中心弹簧失效故障信号周期性变化的幅值增加的较为明显。

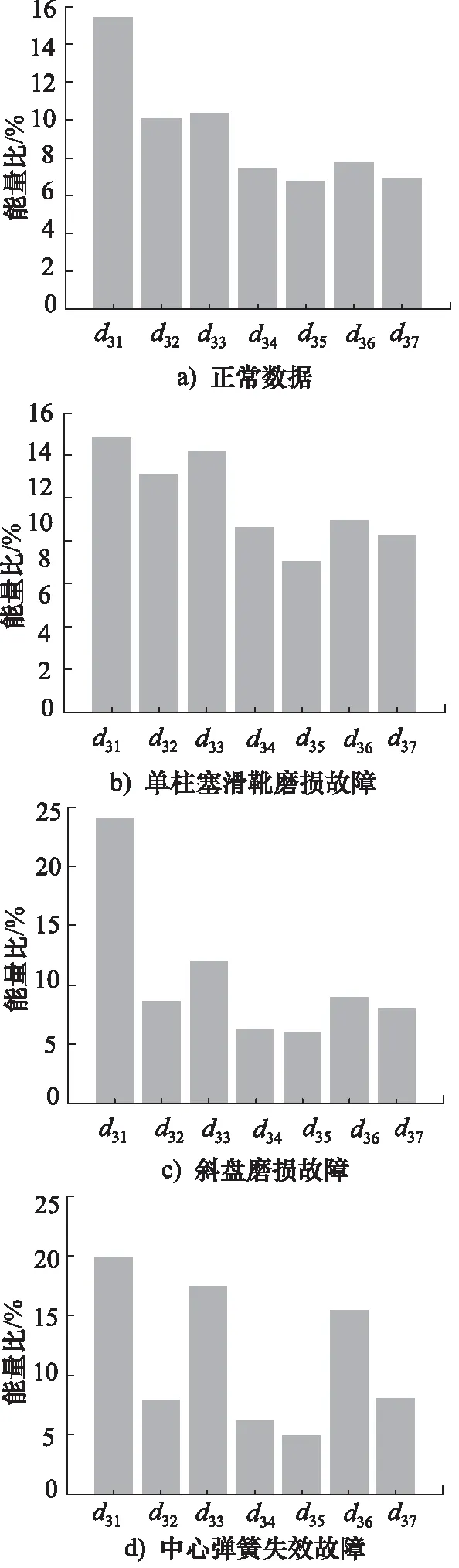
图5 小波包分解对应的能量谱图

4.3 小波脊线解调

采用小波脊线解调方法对重构后的振动信号进行包络解调，然后降低采样频率到2 kHz，得到降采样频率后的包络信号功率谱如图7所示。从图7中可以看出，液压泵处于正常状态时在172.2 Hz基频及其2倍频和3倍频位置出现明显的能量峰值，这种结果与液压泵的振动机理相一致。

从图7a正常状态和图7b单柱塞滑靴磨损故障状态的包络谱比较可以看出，在转轴频率24.6 Hz以及倍频位置，出现了较为明显的幅值增加，而在172.2 Hz基频以及2倍频和4倍频位置幅值增加的幅度较大。故可认为三个频率是反映单柱塞滑靴磨损故障的敏感特征频率。

图6 信号重构后的时域波形

从图7a正常状态和图7c斜盘磨损失效故障状态的包络谱比较可以看出，在转轴频率24.6 Hz以及倍频位置，出现了不同程度的幅值增加，而在24.6 Hz、172.2 Hz基频以及2倍频和4倍频位置幅值增加的幅度最大。故可认为这4个频率可以作为反映斜盘磨损故障的敏感特征频率。

单柱塞滑靴磨损和斜盘磨损均属于滑靴副的故障模式，其故障状态往往会出现相同的特征表现。以上分析过程得出的特征频率相一致的结论印证了这一点。但是故障程度较为接近的两种不同故障在包络谱中特征频率对应的幅值确有明显的区别。斜盘磨损故障对应特征频率的幅值明显高于单柱塞滑靴磨损故障。这是由于斜盘磨损故障会破坏所有柱塞的静压支撑油膜，使柱塞和斜盘的撞击能量增强。而单柱塞单柱塞滑靴磨损只破坏有磨损柱塞的静压支撑油膜，其他柱塞的油膜润滑不受影响，因而柱塞撞击斜盘的能量增加幅度较小。图7b和图7c证实了这个规律。