分块组合搜索的结构稀疏人脸识别模型

蔡体健，徐君，谢昕

（1.中南大学信息科学与工程学院，湖南长沙410075；2.华东交通大学信息工程学院，江西南昌330013）

分块组合搜索的结构稀疏人脸识别模型

蔡体健1，2，徐君2，谢昕2

（1.中南大学信息科学与工程学院，湖南长沙410075；2.华东交通大学信息工程学院，江西南昌330013）

摘要：介绍一种新的稀疏表示人脸识别模型，在经典的稀疏表示分类模型基础上，利用数据字典的结构信息，考虑算法实现的可行性，提出了一种分块组合搜索的稀疏表示人脸识别模型，主要思想是将数据字典按类别自然分块，然后在数据块内进行组合搜索，再联合不同类别的组块，以寻找表示能力最强的组块。为验证模型的性能，使用结构贪婪算法实现分块组合搜索方法和其他的结构稀疏方法，并进行比较，实验显示分块组合搜索的人脸识别率高于其他结构稀疏方法，且此方法性能稳定，不受数据字典排列的影响。

关键词：人脸识别；压缩感知；结构稀疏；组合搜索；结构贪婪算法

随着压缩感知理论的发展，基于稀疏表示人脸识别方法得到广泛的关注，基于稀疏表示的人脸识别方法是将待识别的人脸图像yRn表示成训练样本图像DRn×p的稀疏线性组合，即：y=D，其中Rp是y在字典D下的表示系数，在已知y和D的条件下，可通过压缩感知重构算法求解稀疏表示系数，然后通过分析稀疏表示系数对样本进行判别归类。SRC（sparse representation-based classification）［1］模型是经典的基于稀疏表示的分类模型，SRC模型合并各类别的表示子空间，构成联合子空间，来共同表示测试数据，在联合字典中每个类的数据都为待测数据的表示做贡献，如果某个类贡献得多，则其他类就贡献得少，分类的依据就是判断到底哪个类在竞争表示中贡献得多。在SRC的基础上，文献［1-3］提出了鲁棒的SRC模型（R-SRC），R-SRC添加了一个单位矩阵到SRC的联合字典，形成了一个过完备字典，并利用这个单位矩阵来表示异常数据，使得模型对噪声和遮挡具有很强的鲁棒性能。文献［4］综合了此类稀疏分类模型，将各种保真函数与惩罚函数相结合，得到适合不同条件的人脸识别模型，统称为竞争表示模型（collaborative representation based classification，CRC）。文献［5］提出了扩展的SRC模型（ESRC），ESRC模型假设各类别共享相同的环境条件，其字典不仅包含训练样本，还包括各类别的类内差异，ESRC模型可以应用于单个训练样本的情况下。

稀疏表示分类模型在人脸图像遮挡和噪声处理方面具有较好的识别性能，但传统的稀疏分类模型在数据重构时，仅利用了数据稀疏性的先验知识，大量的结构信息有待挖掘利用。已有文献［6-7］提出组结构的稀疏表示分类模型（group sparse representation-based classification，GSRC），此模型利用了数据字典的组块特性，限制了搜索空间，从而提高了人脸识别的性能。但同时人们也发现这种预定义的、定长的组结构仅适合于类内差异较小的数据字节典；如果类内差异较大，则这种定长组结构不仅不能改善系统性能，而且可能会起到相反的作用。因此人们考虑更细致的组划分方式，文献［7-8］提出将类内样本进一步划分成若干个更小的组块，一定程度上减轻了组块划分不当所造成的影响，但这种方式所得到的仍然是定长的组结构，仍存在组内差异较大的问题。图结构［9-11］是比组结构更一般的数据结构，其组划分是动态的、可重叠的，并不需要预先知道组划分情况，而是根据数据之间的关系动态地形成数据组。动态线性组结构是一种一维的图结构，其动态的组划分特性使得它具有更大的灵活性，更能准确地描述数据之间的关系。

1　从经典稀疏分类模型到结构稀疏分类模型

1.1经典的稀疏分类模型

经典的SRC模型将一个人脸识别问题转变为一个稀疏表示问题，即将测试数据表示成数据字典的稀疏线性组合。SRC的数据字典可由所有类别的训练样本构成，假设训练样本有m个类别，每类别有q个训练数据，则D=[d11,…,d1q,…,di1…diq,…,dm1,…,dmq]，其中[di1,…,diq]是第i类的训练样本，如果y是第i类的测试数据，则在理想的情况下，通过稀疏重构所获得的表示系数中，字典原子[di1,…,diq]所对应的系数项为非0，而其他项为0，即表示系数=[0,…,0,i1,…,iq,0,…,0]应该是稀疏的，应该只有1/m个非0项，测试数据可表示为y=[di1,…,diq][i1,…,iq]T。SRC模型通过寻找测试数据在训练样本基下的最稀疏的线性表示来进行分类，当表示系数足够稀疏时，以上稀疏表示问题可等价于以下最优化问题

在有噪声的情况下，测试数据y=y0+e，y0可表示为训练字典D的稀疏线性组合，噪声eRn可表示为单位矩阵ΛRn×n的稀疏线性组合，将训练字典和单位矩阵合并可构成新的字典基[D Λ]，y可表示为新基下的稀疏线性组合，通过以下的稀疏重构可以获得y的稀疏表示系数：

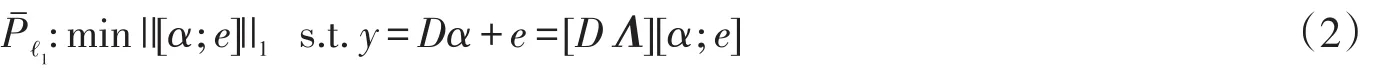
1.2组结构稀疏分类模型

经典的SRC模型将每个字典原子分隔开来，独立处理，没有考虑各原子之间的关系，所产生的稀疏是非结构的。近年来，研究人员发现除了稀疏以外，如果引入字典原子之间的相关性先验信息，可提高稀疏表示的精度以及增强识别的鲁棒性，所产生的稀疏被称为结构化稀疏。

在SRC模型中，训练样本按类排列，同类的样本排列在一起，使数据字典具有明显的组块结构，在类内样本差异不大时，同类的数据划分为一个组，可制约数据的选择，进而提高系统性能；但是当类内样本之间存在较大的差异时，如果仍强制这些数据在一个组，则组内数据的影响互相抵消，反而会降低数据的分类结果。因此人们考虑采用聚类方法或非线性流行学习的方法，将类内样本进一步划分为多个等长的小组，如图1所示，Dij是表示第i类第j个小组，一个类会被划分为多个小组。

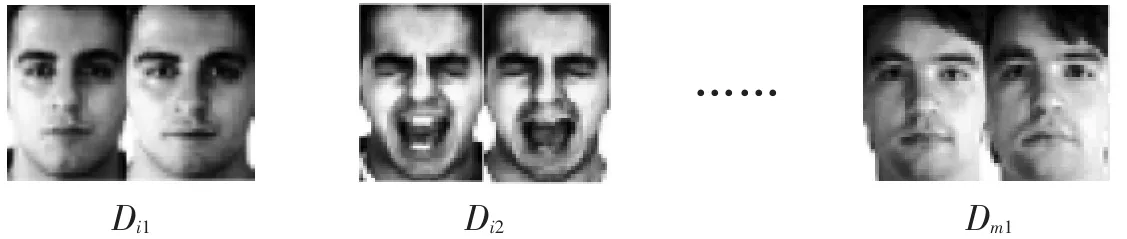
图1　每个类别的训练数据被进一步划分为更小的组块Fig.1 The training images in one class being further divided into multiple small group spaces

若数据字典的每个类别被分为g个等长的小组，则对应的表示系数将有m×g组块，组结构稀疏重构可以表示成以下最优化问题

1.3分块组合搜索的稀疏分类模型

以上细分小组的方法在一定程度上减轻了组块划分不当所造成的影响，但这种方式所得到的仍然是定长的组结构，小组划分仍然不够灵活，组内的差异仍然会影响分类效果。为此可以采用动态可重叠的组合搜索方式，搜索所有可能的组合来寻找表示能力最强的组块。但是如果对搜索不加限制，很容易产生组合爆炸，造成不可行计算。为了减少搜索空间，可以仅搜索固定长度的小组块，例如长度为2或长度为3的组块，把这些小组块作为基块，以基块的联合来表示其他形式的组块。若基块的索引集合称为基子集B，它是表示系数索引集I的子集，I=b，则任何一个组块的索引F都能表示为基子集的并集，F=b。因此通过限制搜索空间，仅搜索基子集空间，可将一个NP的组合搜索问题变为一个可行计算。

此外，还可以进一步采用以下策略减少搜索空间［9-10］：滑动窗口法和分块组合搜索法。以下以一维的表示系数[i1,i2,...,ij,...,iq,(i+1)1,...,(i+1)q,...]（表示系数ij对应着第i类第j个训练样本）为例，介绍两种策略如何获得动态可重叠组块。

1.3.1滑动窗口法

滑动窗口法使用一个定长的窗口，在表示系数上滑动以截取组块。如图2所示所截取的是大小为3的组块，包括：[i1,i2,i3]、[i2,i3,i4]、[i3,i4,i5]……，这样截取的组块是有重叠的，且每个组块是由相邻连续的元素构成。这种分组方法比较适合自然数据，因为自然数据都具有一定的连续性。对于SRC模型其数据字典是人为排列的，并没有这样的连续性，因此数据字典的排列会严重影响系统性能。滑动窗口分组方法利用了数据的连续性，但显而易见，它是一种近似方法，还有许多组块并没有考虑到，例如[i2,i5,i8]等这些非相邻元素构成的组块。

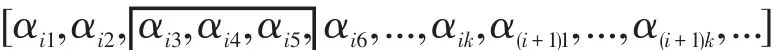
图2　滑动窗口在表示系数上截取组块Fig.2 Sliding window intercepts chunks in the coefficient

1.3.2分块组合搜索法

在数据维数较大时，组合搜索会产生非常大的计算量；但数据量不大时，组合搜索是有可能的。为此人们考虑将数据进行分块，然后在数据块内进行组合搜索，再联合各数据块的搜索结果。由于SRC模型的数据字典是按类排列，对应的表示系数可以按类别自然分块，在每个类别的训练样本数不多的情况下，可以对类内系数进行组合搜索，搜索指定长度的所有组合，假如第i类有5个训练样本，则长度为3的组块包括：[i1,i2,i3]、[i1,i2,i4]、[i1,i2,i5]、[i1,i3,i4]、[i1,i3,5]、[i1,i4,i5]、[i2,i3,i4]、[i2,i3,i5] [i2,i4,i5]、[i3,i4,i5]共10个组，其中包括不相邻元素构成的组块。

以上两种动态分组的方法都是以类别为界线，对类内数据进行动态分组，而类间仍然是固定长度的组划分，将类间的定长组结构与类内的动态线性组结构相结合，形成了一种混合的结构，为了正式地描述混合组结构稀疏模型，假设数据字典有m个类别，i[1,m]，若第i类有gi个不相邻组，ij表示第i类第j个组的表示系数，则混合组结构稀疏重构可表示为

为了区分两种动态分组方法：滑动窗口法和分块组合搜索法，我们分别用Pstruct1和Pstruct2表示它们的稀疏模型。相应的带噪声的混合组结构稀疏重构可表示为：

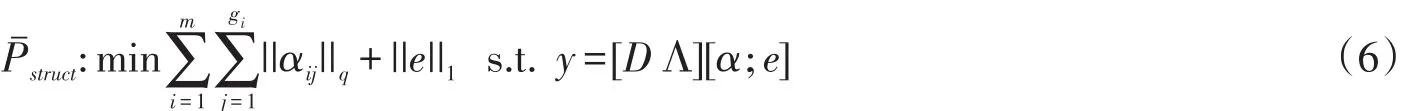
2　实现算法

实现可重叠的动态组稀疏重构的算法较多，在此选用结构贪婪算法（structured greedy algorithm，SGA）［12］。SGA算法是正交匹配追踪（orthogonal matching pursuit，OMP）算法对结构稀疏的扩展。OMP算法在每次迭代中总是选择局部最优的一个原子进入活动集；而SGA算法在每次迭代中总是选择局部最优的基块进入活动集。

SGA算法在预处理阶段，需要确定有限的基子集空间。不同要求的结构稀疏具有不同的基子集空间：对于标准稀疏，其基子集空间是由单元素构成；对于组结构稀疏，其基子集空间是由定长的组块构成，例如长度为3的组块；对于动态可重叠组结构稀疏，可通过滑动窗口法或分块组合搜索法获得其基子集空间；对于鲁棒的稀疏分类模型，其噪声部分的表示系数可以采用标准稀疏类似的方式处理，然后将两部分基子集联合构成搜索空间B=B⋃Be，其中B是表示系数所对应的基子集空间，而Be是噪声部分的表示系数所对应的基子集空间。

SGA算法在每次迭代过程中，需要选择局部最优的基块进入活动集，由于基块的大小可以不同，因此不能仅考虑数据的逼近尺度，还应考虑此基块对稀疏度的影响。为此引入了编码复杂度的概念，利用编码复杂度反衬数据的稀疏度。表示系数的复杂度可以简单地用公式：c()=gln(p)+||来计算，其中p为表示系数的维数，g为动态组个数，如果基块与已有的活动集的元素相邻，则动态组个数g不会增加，编码复杂度仅增加了表示系数的支撑集大小；但如果基块没有与活动集相邻，则动态组个数增加，编码复杂度增加较大，因此可以通过对编码复杂度的惩罚来限制此类基块的选择。通常用以下公式计算结果作为基块选择的依据

3　实验与结果分析

实验选择了AR剪裁的人脸库［13］和扩展的YaleB［14］人脸库。AR库中共有100个人的2 600张图像，被平分为两个子集，每个子集中每人有一张标准照，以及不同表情、光照、带墨镜、戴围巾的照片各三张。扩展的YaleB人脸库中共有38个人，每人64张图像，共2 414张（其中有18张图像损坏）不同光照的人脸图像，根据光照角度不同，被分为五个子集。为运行方便，所有图片用下采样方式降维，每个训练样本被堆叠为一维数据，数据字典进行了二范数规格化处理。实验所选用的机器是华硕笔记本电脑，CPU为i7-4700HQ，四核2.4 G，4 G内存，基于x64处理器的windows8操作系统。

3.1不同结构稀疏的比较与分析

为了比较不同组块划分方式所形成的结构稀疏对人脸识别性能的影响，以下使用SGA算法分别实现动态组结构（包括滑动窗口法Pstruct1和分块组合搜索法Pstruct2）、定长组结构Pℓ2/ℓ1和单元素结构Pℓ1的稀疏重构，实验的训练集中每人有8张图片，来自AR库的子集1，包括不同表情、光照、带墨镜、戴围巾的照片各两张，测试集为AR库的子集2中的不同表情、光照、带墨镜、戴围巾的照片。根据字典的数据结构特点，我们将基块的大小设置为2，定长组结构的组块大小也设置为2，比较4组结构稀疏的人脸识别性能，实验结果如图3、图4所示，图3是各类样本在不同结构稀疏下，所产生的平均人脸识别错误率；图4是对应的平均人脸识别时间。由图可知，分块组合搜索法所得到的人脸识别错误率最低，在相近的运行时间内，Pstruct2所得到的人脸识别错误率与Pstruct1、Pℓ2/ℓ1、Pℓ1相比较，分别降低了10%、12%、13%。分块组合搜索法在更广的范围内寻找表示能力强的组块，因而在人脸识别过程中，能找到与测试图像最接近的样本，人脸识别率能得到显著提高。

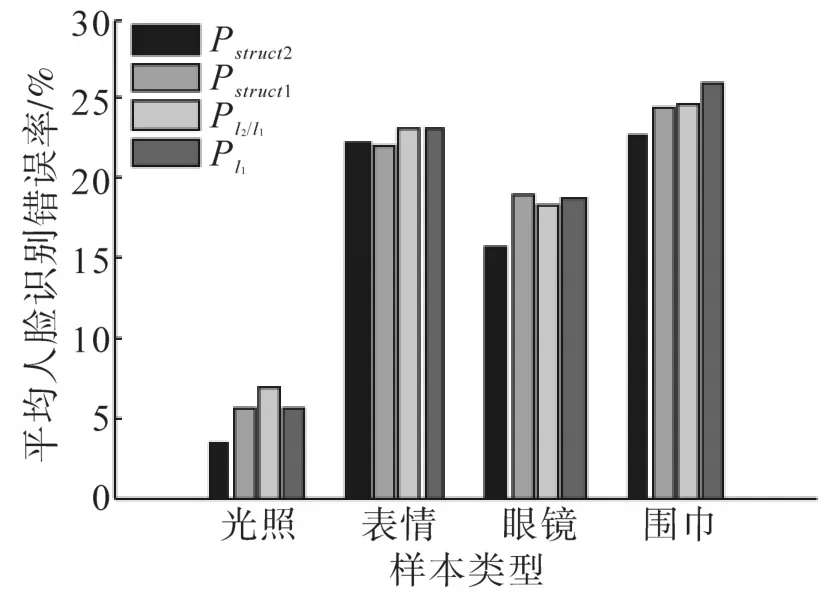
图3　AR库中各类样本在不同结构稀疏下，所产生的平均人脸识别错误率Fig.3 The average recognition error rates obtained by different structure sparse reconstruction in four types of samples of AR

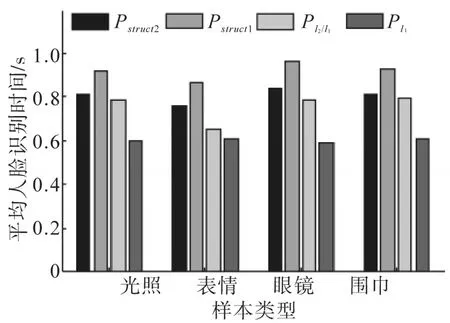
图4　图3对应的平均人脸识别时间Fig.4 The average recognition time corresponding to Fig.3

3.2训练样本的排列顺序对人脸识别的影响

为了验证数据字典中类内样本的排列顺序对人脸识别性能的影响，本实验使用与4.1相同的实验环境，使用同样的训练集和测试集，仅改变训练集类内样本的排列顺序，比较改变排列前后的人脸识别错误率，结果如表1所示。由表可知，改变样本的排列不会影响分块组合搜索和单元素的稀疏重构，因为数据字典类内样本排列顺序无论如何改变，分块组合搜索法及标准稀疏的搜索空间都没有改变，因此这两种方法的人脸识别性能不受数据字典排列顺序的影响，具有一定的稳定性；但类内样本排列的改变会明显影响滑动窗口和定长组结构的稀疏重构，严重时影响率达到24%。

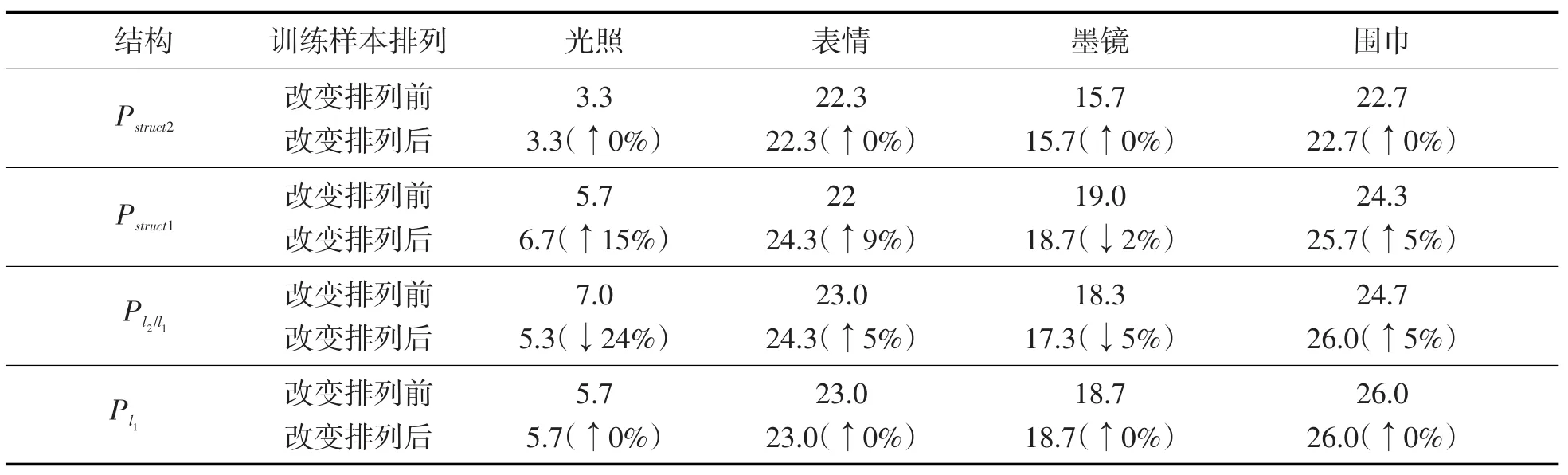
表1　数据字典类内样本改变排列前后的人脸识别错误率Tab. 1 Face recognition error rates before and after changing the arrangement of the intra-class sample in the dictionary

3.3含噪声的人脸识别

为了验证在含噪声的情况下，不同的结构稀疏对人脸识别性能的影响，我们改进了鲁棒的SRC模型，对R-SRC模型中噪声部分所对应的表示系数，仅考虑其稀疏性，即其基子集空间仅包含单元素基块，并与其他表示系数的基子集空间相联合，构成混合的搜索空间。实验中选择了数据较丰富的扩展的YaleB人脸库，每张图像被处理为132×1像素，训练集是从YaleB的子集1和子集2中随机选择的9张图片，基块大小设置为3，定长组大小也设置为3；测试集使用子集3，人为地为每个测试图像添加10%到60%的噪声，每个实验做20次。实验的结果如图5所示。

3.4与其他算法的比较

本节实验进一步使用SGA算法实现不同结构的稀疏重构，同时与一些经典的压缩感知重构算法开展比较。对于AR库，每人随机抽取9张图片构成训练字典，字典中包括戴眼镜、带围巾等各类样本，将字典以外的样本做测试集；对于扩展的YaleB库，每人随机抽取18张图片构成训练字典，其他的做测试集。应用SGA算法、谱投影梯度的l1最小化算法（spectral projected gradient for l1minimization，SPGL1）［15］、快速迭代收缩阀值算法（fast iterative shrinkage-thresholding algorithmn，FISTA）［16］、正交匹配追踪算法（orthogonal matching pursuit，OMP）［17］实现不同结构稀疏重构，每个实验做20次，平均的人脸识别的结果如表2所示。由表可知，定长组结构时，SGA算法能取得较好的识别率，分块组合搜索的SGA算法又优于定长组结构的SGA算法；标准稀疏时，SPGL1算法的识别性能较好。但需要注意的是分块组合搜索的运行时间较长，AR库图像分辨率为1 400×1，每类的训练集大小为9，单位人脸识别时间达到2.830 2 s，可见分块组合搜索方法并不适合数据字典较大的情况。

图5　平均人脸识别率随噪声大小的变化曲线Fig.5 The average face recognition rates with a function of the percentage of corrupted

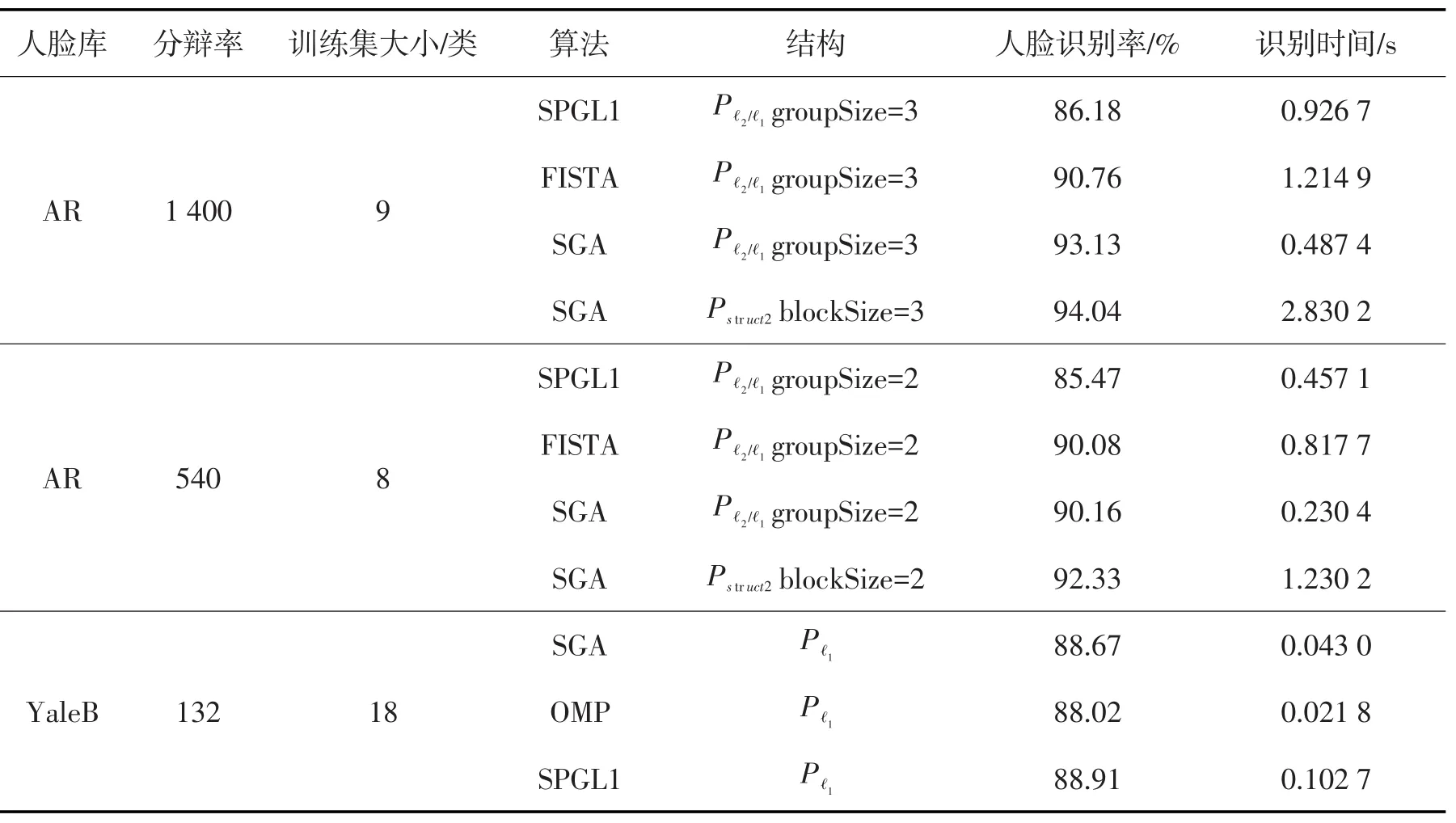
表2　SGA算法与其他算法的人脸识别率比较Tab. 2 The comparison of face recognition rates between SGA and other algorithms

4　　结语

由于数据字典组块划分的不确定性，需要使用搜索的方式寻找表示能力最强的组块，在数据维数较大时，组合搜索会产生非常大的计算量，造成不可行计算。为此考虑先将数据进行分块，然后在数据块内进行组合搜索，再进行组块联合。根据SRC模型的数据字典的特点，将表示系数按类别自然分块，然后对类内系数进行组合搜索，搜索指定长度的所有组合，以寻找局部最优的组块，提高系统的识别性能。最后通过实验验证分块组合搜索的方法其人脸识别率在不同样本、不同分辨率、含噪声等情况下都获得最好的识别性能，且此方法性能稳定，不受数据字典排列顺序的影响，但由于其基子集空间较大，人脸识别时间较长，仅适合数据字典不大的情况下使用。此外对于遮挡、噪声等误差的处理，仅考虑了其稀疏性，今后可以进一步考虑遮挡、噪声的连续性等结构特征。

参考文献：

[1] YANG A Y, ZHOU Z, MA Y, et al. Towards a Robust Face Recognition System Using Compressive Sensing[C]//Eleventh Annual Conference of the International Speech Communication Association. Chiba Makuhari, 2010: 2250-2253.

[2] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2009, 31(2): 210-227.

[3]郑轶,蔡体健.稀疏表示的人脸识别及其优化算法[J].华东交通大学学报, 2012, 29(1): 10-14.

[4] ZHANG L, YANG M, FENG X, et al. Collaborative representation based classification for face recognition[J]. arXiv preprint arX⁃iv,1204, 2358, 2012.

[5] DENG W H, HU J N, GUO J. Extended SRC:undersampled face recognition via intraclass variant dictionary[J]. IEEE Transac⁃tions on Pattern Analysis and Machine Intelligence, 2012,34(9):1864-1870.

[6] MAJUMDAR A, WARD R K. Classification via group sparsity promoting regularization[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. ICASSP, 2009: 861-864.

[7] ELHAMIFAR E, VIDAL R. Robust classification using structured sparse representation[C]//2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2011:1873-1879.

[8]胡正平,宋淑芬.原子稀疏结合块结构稀疏的联合表示图像识别算法[J].信号处理, 2013,29(7):888-895.

[9] JENATTON R, AUDIBERT J Y, BACH F. Structured variable selection with sparsity-inducing norms[J]. Journal of Machine Learning Research, 2011,12:2777-2824.

[10] BACH F, JENATTON R, MAIRAL J, et al. Structured sparsity through convex optimization[J]. Statistical Science, 2012,27(4): 450-468.

[11] SCOTT S L, VARIAN H R. Predicting the present with bayesian structural time series[J]. International Journal of Mathematical Modelling and Numerical Optimisation, 2014,5(1):4-23.

[12] HUANG J, ZHANG T, METAXAS D. Learning with structured sparsity[J]. Journal of Machine Learning Research, 2011,12: 3371-3412.

[13] MARTINEZ A M, BENAVENTE R. The AR Face Database[R].CVC Technical Report#24, June 1998.

[14] GEORGHIADES A S, BELHUMEUR P N, KRIEGMAN D J. From few to many: illumination cone models for face recognition under variable lighting and pose [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001,23(6):643-660.

[15] FRIEDLANDER M, VAN D B, E SPGL1, a solver for large scale sparse reconstruction [J]. SIAM Journal on Scientific Comput⁃ing, 2008,31(2):890-912.

[16] YANG A Y, SASTRY S S, GANESH A, et al. Fast ℓ1-minimization algorithms and an application in robust face recognition: A review[C]//2010 17th IEEE International Conference on Image Processing (ICIP). IEEE, 2010:1849-1852.

[17]蔡体健,樊晓平.贪婪追踪系列算法的分析与优化[J].小型微型计算机系统, 2014,35(5):1116-1119.

（责任编辑姜红贵）

Face Recognition Model of Structural Sparse with Intra-class Combined Search

Cai Tijian1,2,Xu Jun2, Xie Xin2
(1.School of Information and Science Engineering, Central South University, Changsha 410075, China; 2. School of Information Engineering, East China Jiaotong University, Nanchang 330013, China)

Abstract:The paper introduces a new face recognition model of sparse representation, which is based on the clas⁃sical model of sparse representation-based classification (SRC), and utilizes the structure prior information of the data dictionary. Considering the feasibility of the algorithm, it proposes the face recognition model of structural sparse with intra-class combined search that the data dictionary is chunked by natural class, all combinations of specified length are searched in class and blocks in different class are combined to look for the block which can best represent test data. In order to verify the performance of the model, it uses the structured greedy algorithm to realize intra-class combined search and other structural sparse, and compares their performance of face recogni⁃tion. The experiments show face recognition rates of the model with intra-class combined search are higher than other structural sparse, and the model has stable performance which is not affected by the arrangement of the data dictionary.

Key words:face recognition; compressed sensing; structural sparse; combined search; structured greedy algorithm

作者简介：蔡体健（1968—），女，副教授，博士研究生，主要研究方向为智能信息处理、压缩感知、模式识别与人工智能。

基金项目：江西省自然科学基金（20132BAB201027，20142BAB207007）；教育部人文社会科学研究青年基金（14YJCZH172）；华东交通大学科研基金（09111004）

收稿日期：2014-11-08

文章编号：1005-0523（2015）03-0114-08

中图分类号：TP391.4

文献标志码：A