圆中空夹层钢管混凝土压弯剪构件工作机理研究

黄 宏，朱 琪，孙 微，曾根平

（1.华东交通大学土木建筑学院，江西 南昌330013；2.江西省建筑过程模拟与控制重点实验室，江西 南昌330013）

中空夹层钢管混凝土是在两个同心放置的钢管中间填充混凝土而形成的新型组合结构，继承了普通钢管混凝土的承载力高、延性好、施工方便、耐火性能好、经济效果好等优点，又具有截面开展、抗弯刚度大、自重轻、抗震性能好等特点。当中空夹层钢管混凝土被用于实际工程中时，中空夹层钢管混凝土柱间设有斜撑的节点处，大跨重载梁的梁柱节点区域等，是明显的压弯剪复合受力状态，而国内外对中空夹层钢管混凝土压弯剪构件研究报道尚少，因此有必要对其进行研究。本文拟对图1所示截面形式的圆中空夹层钢管混凝土构件进行研究。

国内外已有研究者对实心钢管混凝土构件剪切及其复合受力性能进行了试验研究和理论分析。徐春丽（2004）［1］对54个钢管混凝土柱进行了抗剪承载力试验研究。钱稼茹等（2007）［2］对35根钢管混凝土柱试件进行静力加载试验，建立其受剪承载力计算式。方小丹等（2010）［3］对26个钢管混凝土短柱压弯试件进行了受剪承载力试验研究。蔡建等（2012）［4］对6个方钢管混凝土柱弯剪和压弯剪受力状态下的力学性能进行抗剪承载力试验研究。韩林海等（1994）［5］用纯扭构件全过程分析方法对钢管混凝土组合材料综合剪切物理指标及钢管混凝土抗剪切强度进行了探讨。尧国皇（2006）［6］采用有限元法对钢管混凝土构件压弯剪受力状态下的荷载-变形关系曲线进行了全过程分析。张旭（2009）［7］进行了圆钢管混凝土横向受剪构件抗剪承载力的有限元分析。史艳莉等（2010）［8］采用有限元法对矩形截面钢管混凝土构件纯剪受力下极限抗剪承载力进行了分析。Uenaka K（2013）［9］对径厚比较大的圆中空夹层钢管混凝土梁构件纯剪受力下抗剪承载力进行了试验研究。

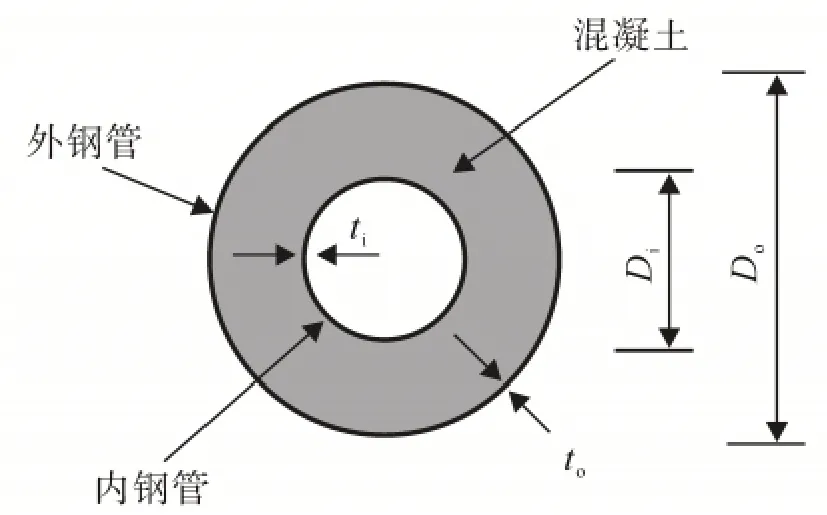
图1 构件截面示意图Fig.1 Schematic view of member section

本文采用有限元方法对圆中空夹层钢管混凝土压弯剪构件的荷载-变形关系曲线进行计算，分析混凝土强度、内外钢管屈服强度、轴压比、截面名义含钢率及空心率对圆中空夹层钢管混凝土压弯剪构件的荷载-变形关系曲线的影响规律，并对圆中空夹层钢管混凝土压弯剪典型构件的荷载-变形全过程曲线进行计算，通过计算结果的全过程分析来研究圆中空夹层钢管混凝土构件在压弯剪作用下的工作机理。

1 有限元模型的建立

利用有限元软件ABAQUS进行建模，对圆中空夹层钢管混凝土压弯剪构件的荷载-变形全过程曲线进行计算。

1.1 单元类型和划分

盖板、内外钢管和混凝土均采用八节点减缩积分格式的三维实体单元（C3D8R）［10］。模型截面采用结构化网格划分技术对模型截面进行划分，在模型的长度方向上进行均匀的网格划分。

1.2 材料的本构关系模型

钢材的本构关系模型采用ABAQUS 软件中的弹塑性模型，该模型在多轴应力状态下满足经典的Von Mises 屈服准则，采用各向同性的强化法则。低碳软钢采用五段式二次塑流模型来描述其塑性性能的应力-应变关系曲线。钢材弹性模量和泊松比分别取206 000 MPa和0.3。盖板则考虑其为刚性材料，计算时弹性模量和泊松比分别为1×1012MPa和1×10-6。

混凝土的本构关系模型采用混凝土塑性损伤模型。该模型需要分别采用受拉和受压的应力-塑性应变关系来定义材料的性能。对于单调荷载下的受拉混凝土，采用能量破坏准则来考虑混凝土的受拉软化性能即应力-断裂能关系。单轴受压应力-应变关系则采用刘威（2005）［11］改进的钢管混凝土中核心混凝土模型，该模型考虑了核心混凝土受钢管被动约束的特点，更适合有限元软件ABAQUS对核心混凝土受压应力-应变关系的分析。核心混凝土的泊松比μc取0.2，弹性模量按Ec=4 730fc（MPa）计算，其中fc为混凝土圆柱体抗压强度。

1.3 钢管与混凝土的界面模型

盖板和内外钢管均采用绑定（Tie）约束，以保证加载横向位移时，盖板和钢管位移一致。盖板和混凝土的界面模型采用法向硬接触来模拟。内外钢管与混凝土的界面模型由法向的接触和切向的粘结滑移组成，在法向方向参考Beck 和Kiyomiya（2003）［12］的研究方法，采用接触刚度较大的单元来模拟，计算时接触单元刚度为1 000 N·mm-1。在钢管和混凝土的切向，采用库仑摩擦模型来模拟钢管与核心混凝土界面切向力的传递，摩擦系数μ取0.6［10］。

1.4 边界条件

采用如图2所示的模型进行模拟计算，模型一端为固定边界，另一端自由边界。计算时，由于构件是复合受力，采用分步加载方式进行加载，首先采用力加载方式对构件施加轴力，然后采用位移加载方式对构件施加横向位移。荷载均在非固定边界上单元结点施加。

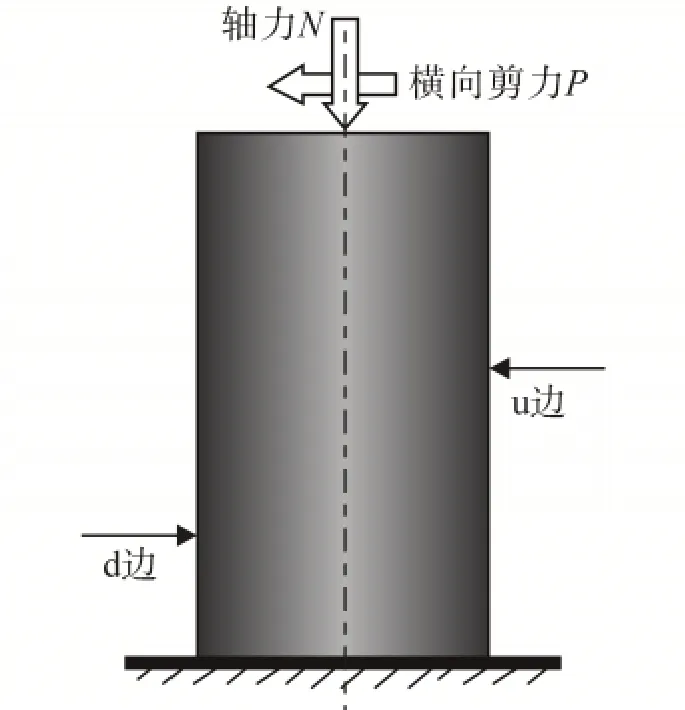
图2 模型边界条件Fig.2 Boundary condition of analytical model

2 荷载-变形关系曲线影响因素分析

影响压弯剪构件横向荷载（P）-变形（Δ）曲线的可能因素有混凝土强度（fcu）、钢材屈服强度（fy）、轴压比（n）、截面名义含钢率（an）、空心率（χ）。通过典型算例分析以上各参数对压弯剪构件P-Δ关系曲线的影响规律。典型算例的基本计算条件为：Do=400 mm；to=9.3 mm；Di=190.7 mm；ti=3.18 mm；fyo=345 MPa；fyi=345 MPa；fcu=60 MPa；an=0.1；n=0.4；χ=0.5；剪跨比m（=L/Do）=2。其中Do为外钢管外径；to为外钢管壁厚；Di为内钢管外径；ti为内钢管壁厚；fyo为外钢管的屈服强度；fyi为内钢管的屈服强度；fcu为混凝土立方体抗压强度；L为构件长度。

图3分别给出了不同混凝土强度、钢管屈服强度、轴压比、截面名义含钢率、空心率时圆中空夹层钢管混凝土压弯剪构件荷载-变形曲线计算结果。

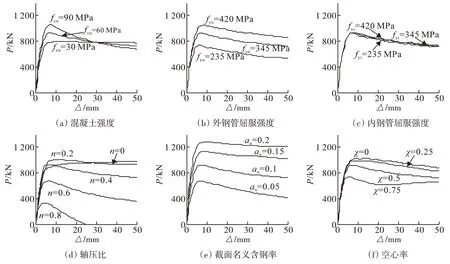
图3 压弯剪荷载-变形曲线Fig.3 Compression bending shear load-displacement curves

从图3中可见，在其它参数一定的情况下：①随着混凝土强度的逐渐提高，夹层混凝土承担的剪力逐渐增大，构件的极限承载力逐渐增大，内外钢管承担的剪力相对降低，延性略有降低，线弹性刚度基本不变。②随着外钢管屈服强度的逐渐提高，外钢管承担的剪力逐渐增大，夹层混凝土和内钢管承担的剪力基本不变，构件的极限承载力逐渐增大，延性和线弹性刚度都基本不变。③内钢管屈服强度的变化对中空夹层钢管混凝土压弯剪试件荷载-变形曲线几乎无影响。④随着轴压比的逐渐增加，内外钢管抗剪承载力降低，轴压比较大时，抗剪承载力降幅较大；而夹层混凝土，当轴压比不大于0.2时，轴力的施加使内外钢管对夹层混凝土的约束作用增大，轴压比越大，夹层混凝土的抗剪承载力反而越大；当轴压比大于0.2时，过大的轴压比使构件过早的进入塑性阶段，随轴压比的增大，夹层混凝土的抗剪承载力下降，因此构件极限承载力先略有增大，曲线无下降段，当轴压比增加到一定值（0.2）后，极限承载力逐渐减小，曲线出现明显的下降段，下降幅度随轴压比的增加而增大，构件延性不断降低，整个轴压比变化过程中线弹性刚度不变。⑤随着截面名义含钢率的逐渐提高，内外钢管承担的剪力逐渐增加，构件的极限承载力逐渐增大，延性略有提高，线弹性刚度基本不变。⑥随着空心率的逐渐提高，夹层混凝土和内外钢管的截面面积有所变化，使得内外钢管承担的剪力增加而夹层混凝土承担的剪力减小；随着空心率的增大，内外钢管与夹层混凝土组合截面的抗剪刚度总体下降，构件的极限承载力逐渐减小，延性基本不变，当空心率到达一定数值时（如l=0.75），钢材所占比例明显增加，剪力大部分有延性较好的内外钢管承担，曲线形状改变，延性提高，整个空心率变化过程中线弹性刚度不变。

3 工作机理研究

对上述典型算例进行计算，研究圆中空夹层钢管混凝土压弯剪构件的破坏模态、荷载-变形曲线及钢管与混凝土间相互作用，揭示其工作机理。

3.1 破坏模态分析

圆中空夹层钢管混凝土外钢管及核心混凝土的破坏模态如图4（a）所示，内钢管破坏模态如图4（b）所示。从图4中可见：圆中空夹层钢管混凝土压弯剪构件破坏时表现出弯曲破坏和剪切破坏的特征，外钢管靠支座处出现局部鼓曲，内钢管靠支座处出现局部凹曲，构件最终因此破坏。圆中空夹层钢管混凝土压弯剪构件中核心混凝土由于受到内外钢管的约束，处于三向受压的应力状态，有效地阻止了混凝土因滑移所产生的脆性破坏，提高了其强度。同时，外钢管由于内填混凝土的存在，使其在受力过程延缓了屈曲失稳的发生，保证了钢材材料性能的充分发挥。因此，由于钢管与核心混凝土之间的相互作用，协同工作，使得中空夹层钢管混凝土压弯剪构件具有较好的力学性能。

3.2 荷载-变形曲线分析

典型算例的荷载-变形全过程曲线如图5所示，图中P为横向荷载，Δ为加载端的横向位移。图6给出了圆中空夹层钢管混凝土典型算例荷载-变形曲线上A点、B点和C点对应的固定边界处内、外钢管和核心混凝土截面纵向应力分布，图中S33为截面纵向应力。圆中空夹层钢管混凝土压弯剪构件的典型P-Δ曲线可分为下面几个阶段：

1）弹性阶段（OA）：在该阶段，P-Δ关系曲线基本呈直线关系，截面的一部分受压区处于卸载状态，另一部分受压区压应力继续增大，在A点，压应力增大受压区外钢管Mises应力达到比例极限（如图6（a）所示）。

2）弹塑性阶段（AB）：A点过后，截面卸载区开始出现拉应力，受压区外钢管和内钢管相继开始屈服。随着横向位移的增加，截面受拉区域的面积不断增加，混凝土截面受压区压应力继续增大，内、外钢管受压区屈服面积不断增加。快接近B点时，受拉区混凝土部分达到受拉极限，退出工作；受拉区外钢管和内钢管相继开始屈服，屈服区域不断增大，构件刚度不断下降。在此阶段，P-Δ关系曲线不再呈直线关系，截面总体处于弹塑性状态（如图6（b）、6（e）所示）。

3）塑性阶段（BC）：B点过后，内、外钢管受拉及受压屈服面积继续增大，直至全截面屈服；混凝土受拉区达到受拉极限截面面积继续增大，退出工作的受拉区混凝土面积增加，受压区混凝土达到应力峰值区域增大，增大至快接近C点时，混凝土受压区靠近内钢管处应力开始下降，且应力下降区域不断扩散，说明靠近内钢管处混凝土已破坏，但由于内、外钢管的约束作用，其应力下降幅度不是很大，仍具有一定的承载力。在此阶段，构件承受的横向剪力由峰值逐渐减小，截面总体处于塑性状态（如图6（c）、6（f）所示）。

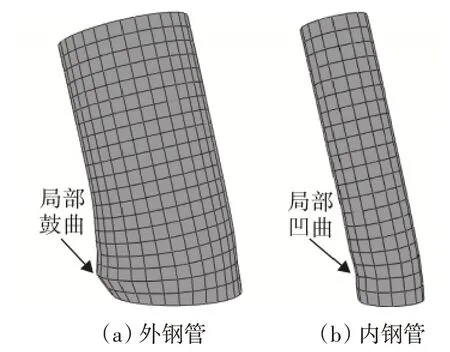
图4 典型压弯剪构件破坏模态Fig.4 Failure modes of members

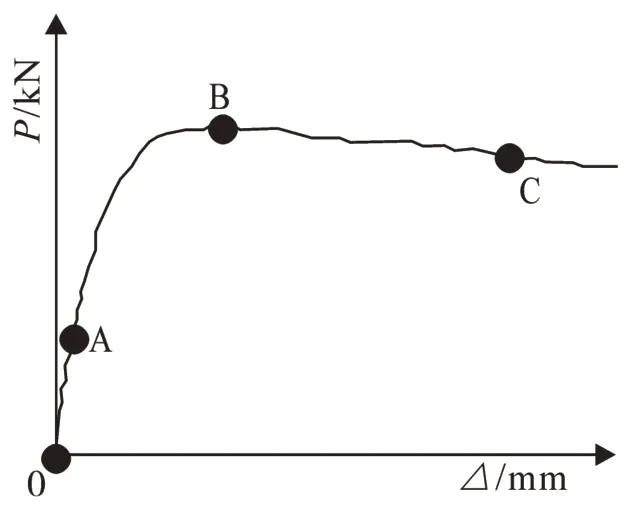
图5 典型压弯剪构件P-Δ关系曲线Fig.5 P-Δ curve of typical compression bending shear

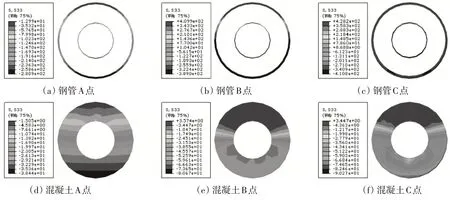
图6 圆中空夹层钢管混凝土压弯剪构件截面纵向应力分布Fig.6 Longitudinal stress distribution of member section

3.3 相互作用分析

图7为典型算例在图5所示的P-Δ关系曲线上A、B、C点时d、u位置处（见图2）内、外钢管与核心混凝土间相互作用力随构件长度坐标分布曲线，其中横坐标0 mm为构件固定端，横坐标800 mm为构件自由端。

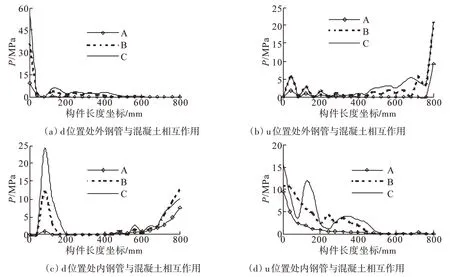
图7 压弯剪构件内外钢管与核心混凝土相互作用力分布Fig.7 Interaction between steel tube and concrete

由图7可见：①由于盖板对钢管的绑定约束，构件两端内、外钢管与核心混凝土间相互作用力比构件其他位置大很多。②在外钢管Mises应力达到比例极限（A点）前，构件大部分范围外钢管与混凝土间相互作用力很小接近于零，内钢管与混凝土在靠近两端部位有一定的相互作用力，这是由于在轴压段及横向荷载施加初始段钢管的泊松比比混凝土大，内、外钢管横向变形均大于混凝土横向变形；随着横向荷载的继续施加，靠近固定端核心混凝土开始发展微裂缝，由于微裂缝的扩展，使得混凝土的横向变形超过了外钢管的横向变形，这样两者之间产生了较大的相互作用力（如图7（a）、7（b）所示），内钢管由于混凝土裂缝扩展产生横向变形的挤压以及自身向外横向变形趋势的双重作用，在靠近固定端位置与混凝土间相互作用力大幅度增大（如图7（c）、7（d）所示）。③除构件两端位置，d边外钢管与混凝土间相互作用最大处主要位于距构件固定端1/10～1/4长度范围内（见图7（a）），d边内钢管与混凝土间相互作用力最大处主要位于距构件固定端1/20～1/4长度范围内（见图7（c）），因此构件破坏时外钢管在上述位置发生局部鼓曲，内钢管在上述位置发生局部凹曲（如图4所示）。④除构件两端位置，内钢管与混凝土间相互作用力普遍大于外钢管与混凝土间相互作用力，在构件屈曲破坏处更加明显，表明圆中空夹层钢管混凝土压弯剪构件内钢管对核心混凝土具有很大的约束作用。

4 结论

通过本文的分析可得如下结论：

1）混凝土强度、外钢管屈服强度、轴压比、截面名义含钢率、空心率均会影响圆中空夹层钢管混凝土压弯剪构件荷载-变形曲线，影响其极限承载力及延性，但对线弹性刚度影响不大。

2）圆中空夹层钢管混凝土压弯剪构件典型算例的荷载-变形全曲线可分为三个阶段：弹性阶段、弹塑性阶段和塑性阶段，曲线后期下降段平缓，表明圆中空夹层钢管混凝土压弯剪构件具有较好的塑性性能。

3）圆中空夹层钢管混凝土压弯剪构件除盖板约束的两端外，内、外钢管与混凝土之间的相互作用力最大处主要位于距构件固定端1/20～1/4长度范围内，使得内、外钢管在该范围内分别发生凹曲与鼓曲，最终导致构件破坏。

4）圆中空夹层钢管混凝土压弯剪构件内钢管对核心混凝土也具有很大的约束作用，混凝土受到内、外钢管的共同约束，提高了其强度，同时，内、外钢管由于混凝土的存在，延缓了屈曲失稳。

[1]徐春丽.钢管混凝土柱抗剪承载力试验研究[D].青岛:山东科技大学,2004.

[2]钱稼茹,崔瑶,方小丹.钢管混凝土柱受剪承载力试验[J].土木工程学报,2007,40(5):1-9.

[3]方小丹,林轶,钱稼茹.压弯作用下钢管混凝土短柱受剪承载力试验研究[J].建筑结构学报,2010,31(8):36-44.

[4]蔡健,梁伟盛,林辉.方钢管混凝土柱抗剪性能试验研究[J].深圳大学学报理工版,2012,29(3):189-194.

[5]韩林海,钟善桐.钢管混凝土基本剪切问题研究[J].哈尔滨建筑工程学院学报,1994,27(6):28-34.

[6]尧国皇.钢管混凝土构件在复杂受力状态下的工作机理研究[D].福州:福州大学,2006.

[7]张旭.圆钢管混凝土构件抗剪性能分析[D].哈尔滨:哈尔滨工业大学,2009.

[8]史艳莉,陈宇超,王文达.矩形钢管混凝土构件基本剪切性能研究[J].铁道建筑,2010(3):109-111.

[9]UENAKA K.Concrete filled double skin circular tubular beams with large diameter-to-thickness ratio under shear[J].Thin-Walled Structures 2013,70(9):33-38.

[10]黄宏,李婷,陈梦成.方中空夹层钢管混凝土压弯扭构件数值模拟[J].华东交通大学学报,2013,30(4):24-29.

[11]刘威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学,2005:54-66.

[12]BECK J, KIYOMIYA O.Fundamental pure torsional properties of concrete filled circular steel tubes[J].Materials Conc Struct Pavements,2003,739:285-296.