矩阵方程AX=B的自反解与反自反解及最佳逼近

王婧，刘喜富

（华东交通大学1.国际学院；2.理学院，江西南昌330013）

矩阵方程AX=B的自反解与反自反解及最佳逼近

王婧1，刘喜富2

（华东交通大学1.国际学院；2.理学院，江西南昌330013）

摘要：给定两个广义反射矩阵P，Q，通常对于矩阵方程AX=B关于P，Q的自反解和反自反解的研究大多是通过矩阵分解或广义奇异值分解来进行的。采用广义逆，建立该方程存在自反解和反自反解的充要条件以及解的一般表达式，并研究与之相关的矩阵最佳逼近问题。

关键词：自反解；反自反解；矩阵方程；最佳逼近解

作通者讯简作介者：刘喜富（1984—），男，讲师，博士，研究方向为矩阵与数值代数。

本文用Cn×m表示所有n×m阶复矩阵集合。对于矩阵ACn×n，其迹记为tr(A)。对于矩阵ACm×n，其共轭转置矩阵、值域、F范数和M-P逆分别记为和A+。In表示n阶单位矩阵。并记EA=I-AA+，FA=I-A+A。

由于关于方程（1）的一般解的研究已非常全面，故从上世纪70年代起，该方程的约束解的研究逐渐受到关注，这些约束主要包括：Hermitian、（半）正定、实部（半）正定、（反）自反、对称、中心对称等约束。约束矩阵方程问题在结构力学、固体力学、物理、地质、分子光谱学、电学、量子力学、结构设计、参数识别、自动控制等许多领域都具有重要应用。也正是由于约束解有着广泛的应用，才推动着其理论研究的不断完善。例如，Khatri和Mitra［1］对其Hermitian解和半正定解进行了研究；文献［2-3］对实部半正定解和实部正定解做了系统研究；文献［4］利用矩阵分解技术研究了该方程的P,Q的自反解与反自反解与最佳逼近问题；文献［5］利用广义奇异值分解讨论了它的自反最小二乘与最佳逼近问题。对于方程AHXA=B的反自反解与最佳逼近问题，文献［6-7］同样利用广义奇异值分解对此作了研究。

本文主要利用矩阵广义逆理论重新研究以下两个问题。

问题Ⅱ设问题I的解集SX非空，给定矩阵CCm×n，求SX，使

1　问题I的解

为了证明本文的结论，需要以下引理。

引理1［4］给定ACk×m，BCk×n，XCm×n为未知矩阵。则矩阵方程AX=B有解当且仅当r( ) A B =r(A)，并且此一般解可表示为

其中：V为适当阶数的任意矩阵。

证明由于P为广义反射矩阵，自然也是酉矩阵，根据广义逆的性质有，所以。另外，再根据广义逆的性质M+M=N+N当且仅当可得

另一方面

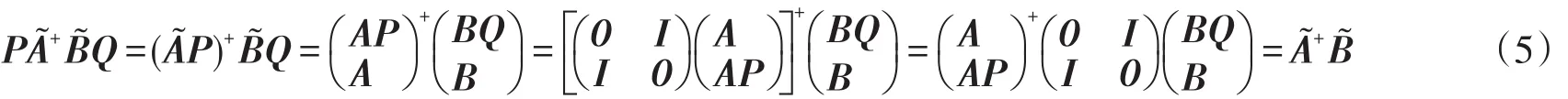
其中：X为方程AX=B和APX=BQ的公共解。

证明设X是AX=B和APX=BQ的公共解，易证AXr=B，且Xr=PXrQ，即Xr是方程AX=B的关于P、Q的自反解。

接下来，给出本文的主要结论。

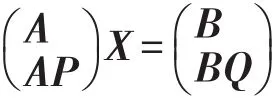
同理可得如下结论。

2　问题Ⅱ的解

根据定理1和定理2的结论，本节将给出问题Ⅱ的最佳逼近解。在此之前，先证明下面关于矩阵范数的两个结论。引理4PCm×m和QCn×n为广义反射矩阵，设，则

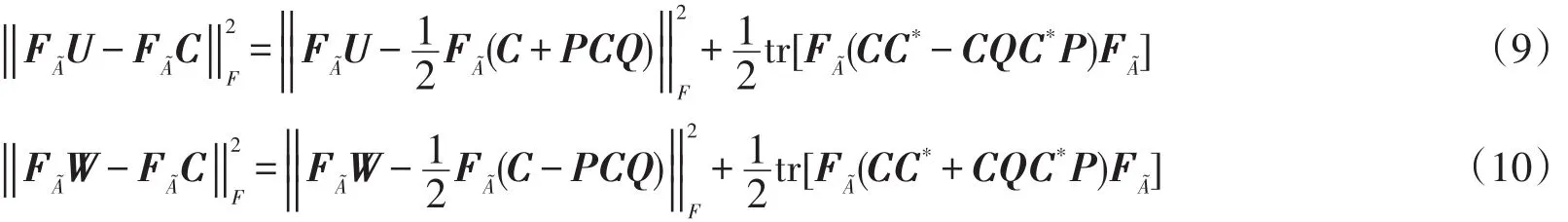
证明由于F范数为酉不变范数，根据假设有

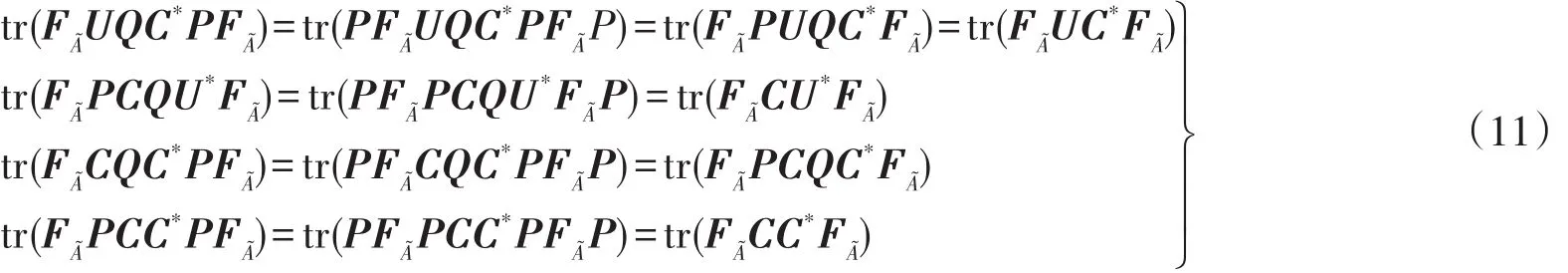
所以

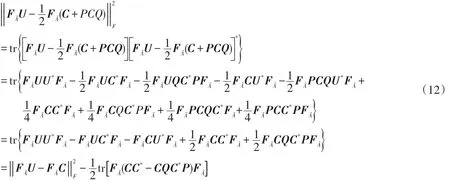
于是，式（9）得证。同理，可得式（10）。证毕。

并且

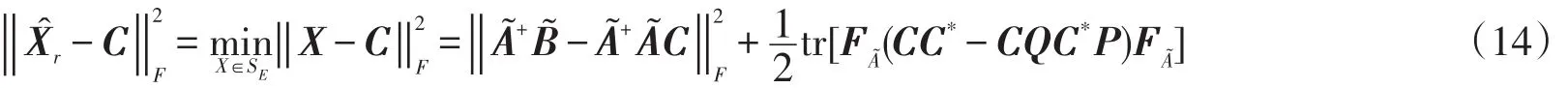
证明设X为AX=B的自反解，根据定理2、引理4，则有

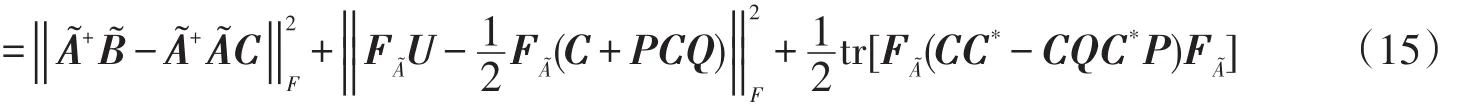
同理，可得如下结论。

并且

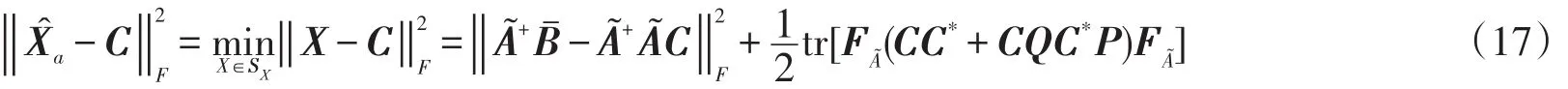
参考文献：

[1] KHATRI C, MITRA S. Hermitian and nonnegative definite solutions of linear matrix equations[J]. Siam J Appl Math, 1976,31: 579-585.

[2] LIU X. Comments on "The common Re-nnd and Re-pd solutions to the matrix equations AX=C and XB=D " [J]. Appl Math Comput, 2014, 236: 663-668.

[3] WU L. The re-positive defininte solutions to the matrix inverse problem AX=B [J]. Linear Algebra Appl, 1992,174:145-151.

[4] ZHANG J, ZHOU S, HU X. The (P,Q) generalized reflexive and anti-reflexive solutions of the matrix equation AX=B [J]. Appl Math Comput, 2009, 209: 254-258.

[5]肖庆丰,胡锡炎,张磊.矩阵方程AX=B的自反最小秩解及其最佳逼近[J].纯粹数学与应用数学, 2012,28(6):719-727.

[6]彭向阳,张磊,胡锡炎.矩阵方程AHXA=B的反Hermitian反自反解[J].曲阜师范大学学报, 2005,31(1):1-6.

[7]王艾红.矩阵方程AHXA=B的反自反解及其最佳逼近[J].长沙大学学报, 2005,19(5):5-9.

（责任编辑姜红贵）

Reflexive and Anti-reflexive Solutions to Matrix Equation AX=B and the Optimal Approximation

Wang Jing1, Liu Xifu2
(1. International School, East China Jiaotong University, Nanchang 330013, China; 2. School of Science, East China Jiaotong University, Nanchang 330013, China)

Abstract:Generally, the main methods to study the P,Q reflexive and anti-reflexive solutions of the matrix equa⁃tion AX=B are the decomposition of matrices and the generalized singular value decomposition of matrices. This paper studies the equation by using the generalized inverse and establishes conditions for the existence and repre⁃sentations of the reflexive and anti-reflexive solutions .Moreover, the optimal approximation solutions are also dis⁃cussed.

Key words:reflexive solution; anti-reflexive solution; matrix equation; optimal approximation

作者简介：王婧（1986—），女，助教，硕士，研究方向为矩阵方程求解。

基金项目：国家自然科学基金项目(11461026)；江西省科技厅项目(20142BAB211010)

收稿日期：2014-12-28

文章编号：1005-0523（2015）03-0122-04

中图分类号：O151.2

文献标志码：A