关于有限集［n］ 及其子集若干性质的讨论*

程　杰，杨冬苹

( 1．重庆师范大学数学学院，重庆401331; 2．重庆市秀山高级中学，重庆409900)



关于有限集［n］ 及其子集若干性质的讨论*

程杰1，杨冬苹2

( 1．重庆师范大学数学学院，重庆401331; 2．重庆市秀山高级中学，重庆409900)

摘要:有限集由于有有限多个子集，因而具有许多无限集合所不具有的性质;从n元有限集的所有k元子集元素和入手，得到了n元有限集的全体子集元素和Sn的计数公式，以及所有k阶子集的元素和S(n，k)( k=0，1，2，…，n)的计数公式以及单峰性质和其他一些推论．

关键词:计数公式;有限集;有限子集;二项式系数

有限集合由于具有有限个子集，因而具有许多无限集合不可比拟的性质．众所周知，有限集合及其子集与组合数学有着非常紧密的联系．首先，有限集的所有子集的元素和就是一个组合数学范畴的问题;再者，其各阶子集的元素和之比与二项式系数有着完美的吻合．通过上述对有限集的讨论，可以得到一系列的结论．

1相关性质

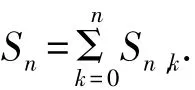
定理1［1］集合［n］的子集个数为2n．

证明令2［n］表示［n］的所有子集组成的集合，再令{ 0，1}n={ (1，2，…，n) :i= 0或1}．因为每个i有两种可能的取值，所以有card( { 0，1}n) = 2n．定义映射( T) = (1，2，…，n)，其中

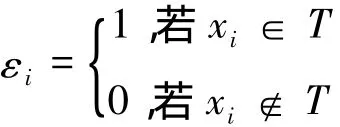
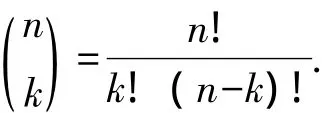
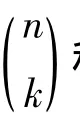
另一方面，这里有n种方法从S中选出一个元素作为排序的第一个元素，然后再有n－1种方法从剩下的元素中选出一个元素作为排序的第二个元素，以此类推，直至有n－k+1种方法从剩下的元素中选出一个元素作为排序的第k个元素．这样就有

证明利用定理2，对于正整数k( 1≤k≤n)，有

2结论

证明对于元素j( 1≤j≤n)，分为属于集合［n］的某一子集或者不属于集合［n］的所有子集2种情况．而元素j不属于集合［n］的所有子集共有2n－1种情况(这相当于集合［n］j的所有子集的个数)，即元素j在集合［n］的子集中共出现2n－2n－1=2n－1次．当j遍历1到n的所有正整数时，就得到集合［n］的所有子集的元素和为

性质2类似于二项式系数列，集合［n］的所有k元子集的元素和Sn，k构成的序列也具有单峰性:当n是偶数时，集合［n］的所有k元子集的元素和Sn，k( k=0，1，2，…，n)中最大的是和;当n是奇数时，集合［n］的所有k元子集的元素和Sn，k( k=0，1，2，…，n)中最大的是．

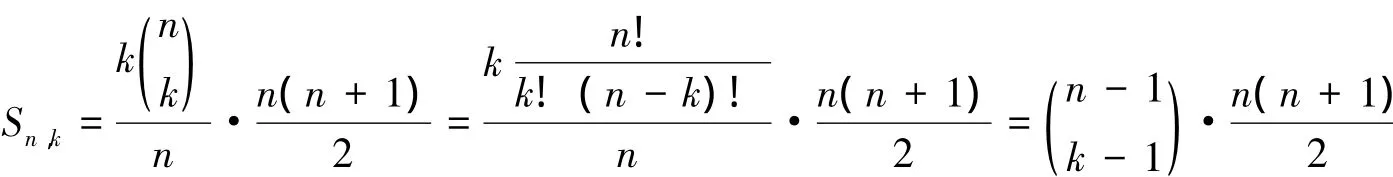
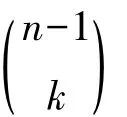
证明由性质2可得，集合［n］的所有k元子集的元素和为

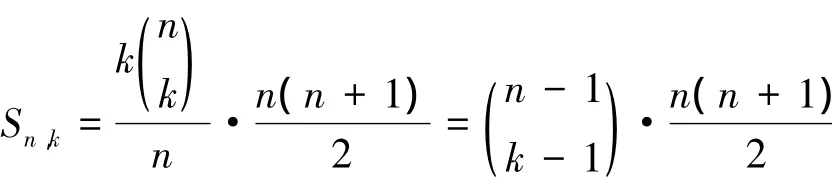
参考文献:

［1］STANLEY P．计数组合学［M］．付梅，等译．北京:高等教育出版社，2009

［2］李乔．组合学讲义［M］．北京:高等教育出版社，2008

［3］曹汝成．组合数学［M］．广州:华南理工大学出版社，2012

Discussion on the Nature of the Finite Set［n］and Its Subsets

CHENG Jie1，Yang Dong-Ping2

( 1．College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China; 2．Chongqing Xiushan High School，Chongqing 409900，China)

Abstract:Because finite set contains limited subsets，it has many properties infinite set doesn’t have．This paper begins with the sum of all elements of subsets with k elements in finite set with n elements，gains calculating formula for Sn，the sum of all elements of subsets in finite set with n elements，and gets calculating formula for S(n，k)( k=0，1，2，…，n)，the sum of all elements of subsets with k order as well as unimodal nature and some other inferences．

Key words:counting formula; finite set; limited subset; binomial coefficients

作者简介:程杰( 1990-)，男，重庆开县人，硕士，从事微分方程与动力系统研究．

*基金项目:重庆市自然科学基金( 2011jjA00003)．

收稿日期:2014－09－20;修回日期: 2014－10－09．

doi:10．16055/j．issn．1672－058X．2015．0005．015

中图分类号:O175

文献标志码:A

文章编号:1672－058X( 2015) 05－0052－03