强Wolfe 条件下一类修正FR 共轭梯度法

张鹏

(重庆师范大学数学学院，重庆401331)



强Wolfe 条件下一类修正FR 共轭梯度法

张鹏

(重庆师范大学数学学院，重庆401331)

摘要:通过适当修正Fletcher-Reeves( FR)方法，提出了一类修正FR共轭梯度法方法( MFR*)，并证明了MFR*方法在强Wolfe线搜索下具有充分下降条件和全局收敛性．

关键词:无约束优化;共轭梯度法;充分下降性;全局收敛性

0引言

考虑无约束优化问题:

其中f: Rn→R是连续可微的函数．共轭梯度法因为迭代简单，存储量小，因此常被用来求解具有问题( 1)形式的大规模优化问题．共轭梯度法的一般迭代格式为

其中，‖·‖为欧几里得范数，yk－1=gk－gk－1．

在共轭梯度法的许多理论分析和数值实现中，常常采用非精确线搜索，如强Wolfe线搜索．强Wolfe线搜索要求步长k满足

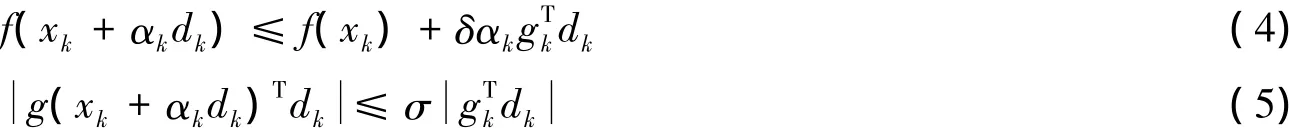
敖卫斌［6］提出一种修正的DY共轭梯度法的全局收敛性，并证明了全局收敛性;黎小林［7］提出一种Glodstein条件下的修正CD共轭梯度法并证明了全局收敛性．

Zhang［8］提出一种修正的PRP方法，其中k被定义为

并证明了NPRP在强Wolfe线搜索下的充分下降性和全局收敛性．

最近，Jiang［9］提出一种修正的FR方法( MFR方法)，其中k具有如下形式

证明了MFR不依赖线搜索，总是产生一个下降方向，并且在强Wolfe线搜索下全局收敛．

受Zhang［8］和Jiang［9］的启发，构造一类如下的修正FR方法，共轭梯度参数k具有如下形式

第2部分给出MFR*算法;第3部分证明了MFR*算法的充分下降性和在强Wolfe线搜索下的全局收敛性．

1算法设计

MFR*算法:

Step1如果‖gk‖≤，则算法终止;

Step3令xk+1=xk+kdk，gk+1=g( xk+1)，如果‖gk+1‖≤，则算法终止;

Step4由式( 3) ( 6)计算dk+1，置k: =k+1，转Step2．

2 MFR*算法的收敛性

假设B目标函数f( x)在水平集L的一个领域N内连续可微，且其梯度函数g满足Lipschitz条件，即存在常数l＞0，使‖g( x)－g( y)‖≤l‖x－y‖，x，yL．

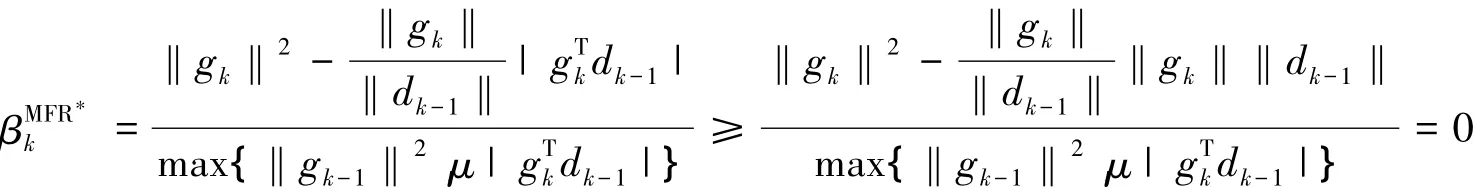
并且有

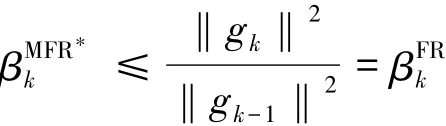
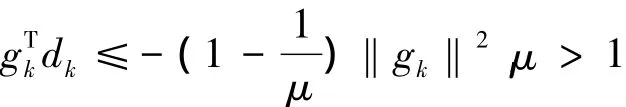
因此

由引理1和文献［10］中的定理3．2，可以直接得到定理1．

定理1若假设( A) ( B)成立，MFR*算法中步长k满足强Wolfe条件式( 4)和( 5)，参数0＜δ＜＜，则

参考文献:

［1］FLETCHER R，REEVES C M．Function Minimization by Conjugate Gradients［J］．The Computer Journal，1964，7( 2) : 149-154

［2］POLAK E，RIBIERE G．Note Sur La Convergence De Methodes De Directions Conjuguees［J］．ESAIM: Mathematical Modelling and Numerical Analysis-Modélisation Mathematique et Analyse Numerique，1969，3( R1) : 35-43

［3］POLYAK B T．The Conjugate Gradient Method in Extremal Problems［J］．USSR Computational Mathematics and Mathematical Physics，1969，9( 4) : 94-112

［4］HESTENES M R，STIEFEL E．Methods of Conjugate Gradients for Solving Linear Systems［M］．NBS，1952

［5］DAI Y H，YUAN Y．A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property［J］．SIAM Journal on Optimization，1999，10( 1) : 177-182

［6］敖卫斌．一种修正的DY共轭梯度法的全局收敛性［J］．重庆工商大学学报:自然科学版，2013，30( 10) : 17-20

［7］黎小林．Glodstein条件下的一种修正CD共轭梯度法［J］．重庆工商大学学报:自然科学版，2014，31( 3) : 24-26

［8］ZHANG L．An Improved Wei-Yao-Liu Nonlinear Conjugate Gradient Method for Optimization Computation［J］．Applied Mathematics and Computation，2009( 6) : 2269-2274

［9］JIANG X，JIAN J．A Sufficient Descent Dai-Yuan Type Nonlinear Conjugate Gradient Method for Unconstrained Optimization Problems［J］．Nonlinear Dynamics，2013，72( 1-2) : 101-112

［10］GILBERT J C，NOCEDAL J．Global Convergence Properties of Conjugate Gradient Methods for Optimization［J］．SIAM Journal on Optimization，1992，2( 1) : 21-42

A Class of Modified FR Method with Strong Wolfe Line Search

ZHANG Peng

( College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

Abstract:This paper proposes a class of modified FR method ( MFR*) by modifying Fletcher-Reeves ( FR)，and proves MFR*with strong Wolfe line search satisfies sufficient descent condition and global convergence．

Key words:unconstrained optimization; conjugate gradient method; sufficient descent condition; global convergence

作者简介:张鹏( 1990-)，男，河南信阳人，硕士，从事全局最优化理论与算法研究．

收稿日期:2014－08－24;修回日期: 2014－10－08．

doi:10．16055/j．issn．1672－058X．2015．0005．006

中图分类号:O224

文献标识码:A

文章编号:1672－058X( 2015) 05－0020－03