一类修正DY 共轭梯度法及其全局收敛性

马文亚

(重庆师范大学数学学院，重庆401331)



一类修正DY 共轭梯度法及其全局收敛性

马文亚

(重庆师范大学数学学院，重庆401331)

摘要:对DY共轭梯度方法进行修正，使得修正的共轭梯度方法( MDY*)在Wolfe线搜索下满足充分下降条件和全局收敛性．

关键词:修正DY共轭梯度法; Wolfe线搜索;充分下降性;全局收敛性

1基础知识

考虑无约束优化问题:

其中f: Rn→R是一个连续可微的函数．

共轭梯度法是求解问题( 1)的具有如下的迭代格式一类方法:

其中，‖·‖为欧几里得范数，yk－1=gk－gk－1．

其中HS方法被公认为是数值效果较好的方法，而DY方法则有较好的收敛性．最近，文献［3］对文献［4］的MHS公式进行改进，得到如下新的k公式:

并证明了由新公式产生的算法在Wolfe线搜索条件下满足充分下降性和全局收敛性．

Dai和Wen［5］对文献［6］的NHS公式进行改进，得到如下新的k公式:

并证明了由新公式产生的算法不仅每步迭代都可以产生一个充分下降方向，且在Wolfe线搜索条件下全局收敛．

在共轭梯度法的许多理论分析和数值实现中，常常使用Wolfe线搜索，其要求k满足

2算法

MDY*算法:

初始步:给定初始点x0Rn，δ( 0，1)，( 0，1)，＞1，＞0，令d0=－g0，k: =0;

步骤1:若g0≤，则停止;

步骤3:令xk+1=xk+kdk，若gk+1≤，则停止;

步骤5:令k: =k+1，转步骤2．

3 MDY*算法的收敛性

为了证明新算法的全局收敛性，首先给出两个假设:

引理1［7］假设( A) ( B)成立，设序列{ gk}和{ dk}由MDY*算法产生，并设步长k由Wolfe线搜索式( 7)、( 8)计算，则

引理2假设( A) ( B)成立，设序列{ gk}和{ dk}由MDY*算法产生，并设步长k由Wolfe线搜索式( 7)、( 8)计算，则对所有的k≥0，有

证明用归纳法证明．

假设n=k－1( k≥1)时，式( 11)成立，则由式( 8)得

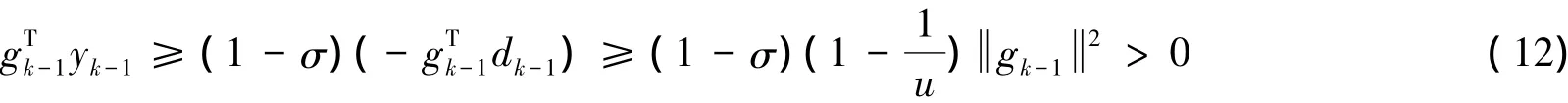
由式( 6)得

因此，有

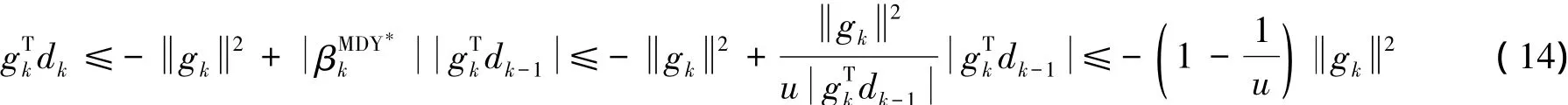
定理1假设( A) ( B)成立，设序列{ gk}和{ dk}由MDY*算法产生，并设步长k由Wolfe线搜索式( 7) ( 8)计算，假设存在一个正常数*满足k≥*，则

证明由假设( A) ( B)知，存在一个常数M＞0，使得

由式( 10)、( 11)、( 16)，知式( 14)成立．

参考文献:

［1］HESTENES M R，STIEFEL E．Methods of Conjugate Gradients for Solving Linear Systems［M］．NBS，1952

［2］DAI Y H，YUAN Y X．A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property［J］．SIAM Journal on Optimization，1999，10( 1) : 177-182

［3］江羡珍，马国栋，简金宝．Wolfe线搜索下的一个新的全局收敛性共轭梯度法［J］．工程数学学报，2011，28( 6) : 779-786

［4］YAO S W，WEI Z X，HUANG H．A Note about WYL＇s Conjugate Gradient Method and Its Applications［J］．Applied Mathematics and Computation，2007( 2) : 381-388

［5］DAI Z F，WEN F H．Another Improved Wei-Yao-Liu Nonlinear Conjugate Gradient Method with Sufficient Descent Property［J］．Applied Mathematics and Computation，2012( 14) : 7421-7430

［6］ZHANG L．An Improved Wei-Yao-Liu Nonlinear Conjugate Gradient Method for Optimization Computation［J］．Applied Mathematics and Computation，2009( 6) : 2269-2274

［7］ZOUTENDIJK G．Nonlinear Programming，Computational Methods，in Integer and Nonlinear Programming［M］．North-Holland，Amsterdam，1970

A Class of Modified DY Conjugate Gradient Method and Its Global Convergence

MA Wen-ya

( College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

Abstract:Dai-Yuan conjugate gradient method is modified to make it satisfy sufficient descent condition and global convergence with Wolfe line search．

Key words:modified Dai-Yuan conjugate gradient method; Wolfe line search; sufficient descent condition; global convergence

作者简介:马文亚( 1988-)，女，陕西杨凌人，硕士研究生，从事最优化计算方法及理论研究．

收稿日期:2014－08－24;修回日期: 2014－10－11．

doi:10．16055/j．issn．1672－058X．2015．0005．005

中图分类号:O224

文献标识码:A

文章编号:1672－058X( 2015) 05－0017－03