含有非线性干扰的时滞竞争性神经网络指数同步

苏婷婷

(重庆师范大学数学系，重庆401331)



含有非线性干扰的时滞竞争性神经网络指数同步

苏婷婷

(重庆师范大学数学系，重庆401331)

摘要:研究了含有非线性干扰的时滞竞争性神经网络的指数同步，基于利亚普洛夫稳定性理论、不等式技巧等，设计了一个简单的控制器，并获得了一些指数同步的充分条件;所得结论简单实际，可以推广到其他神经网络中;最后给出了一个数值模拟来说明结论的有效性．

关键词:竞争性神经网络;指数同步;非线性干扰;时滞

近年来，由于在通信、图像处理、医学等方面的广泛应用，神经网络的同步研究越来越引起更多学者们的关注．竞争性神经网络是重要的神经网络之一，其主要特点是含有两个神经变元，因此研究该网络的同步更具挑战性，并且已取得了很好的结果［1－3］．在实际应用中，网络不可避免地会受到外界环境的干扰，因此在研究中考虑含有非线性干扰的系统很有必要．作者在文献［2－3］中对含有干扰的竞争性神经网络的自适应同步做了研究，然而对于指数同步的研究很少．此外，由于信道的宽度及有限的传播速度，时滞不可避免地存在于网络之中，因此，作者在文献［4－5］中对时滞神经网络的指数同步做了研究．此处重点研究含有非线性干扰的时滞竞争性神经网络的指数同步，通过设计一个简单适用的控制器，得到了一些指数同步的充分条件，并给出了严格的证明，最后数值模拟说明了结论的有效性．

1预备知识

研究如下竞争性神经网络:

其中，第一个方程代表短期记忆变元( STM)，第二个方程指的是长期记忆变元( LTM) ; A = diag( a1，a2，…，an)，ai＞0是神经元的时间常数; B=( bij)n×n，C=( cij)n×n，bij和cij指的是的i个神经元和第j个神经元之间的连接权重，f( x( t) )是外部输入，D=diag( D1，D2，…，Dn)，=diag(1，2，…，n)，=diag(1，2，…，n)，其中Di是外部刺激，i＞0，i表示常数量，x( t)为非线性干扰且满足x( t)≤M1．

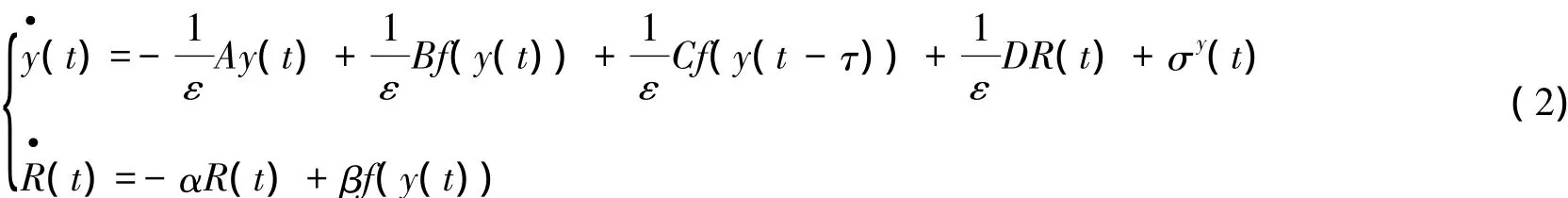
可以得到误差系统为

假设1存在非负的的常数li， 使得式( 4)成立:

引理2［6］假设u( t)，v( t)是［t1，t2］上的连续函数，t1≤t≤t2，T=t2－t1，u( t)≥0，常数≥0，r≥0，如果满足，则

定义1如果存在正的常数M＞1，ν＞0，使得对于所有t≥0，有式( 6)成立:

则系统( 2)指数同步于系统( 1)．

2主要结论

定理1若假设1成立，令控制器为

且K=diag( k1，k2，…，kn)，=diag(1，2，…，n)，其中ki＞0，i＞0，λ为正常数．并且满足不等式( 8)－( 10) :

证明选取Lyapunov-Krasovskii函数如下:

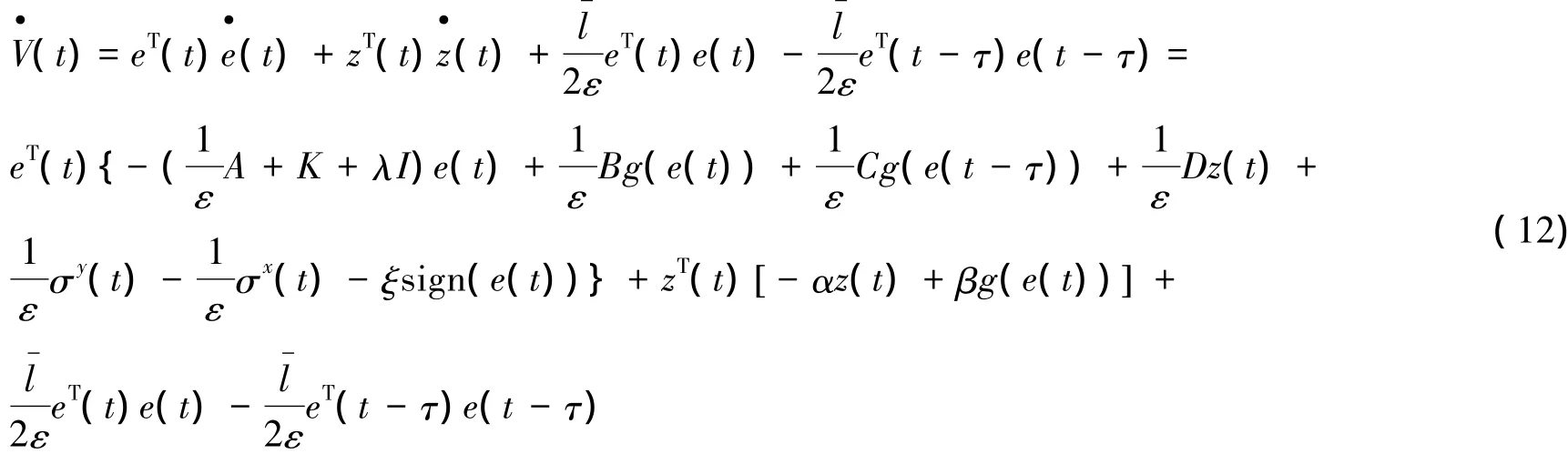
由式( 8)可得

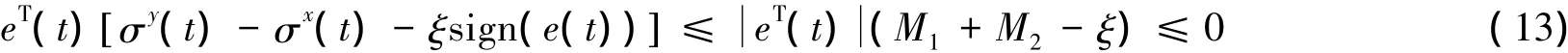
由引理1和假设1，可得到如下不等式:

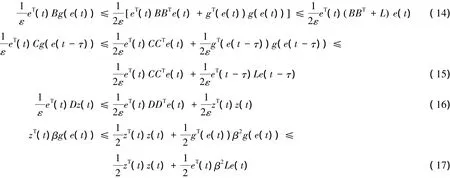
由式( 13)到( 17)可以得到

由式( 9) ( 10)，式( 15)可变为

式( 19)两边积分可得

又知

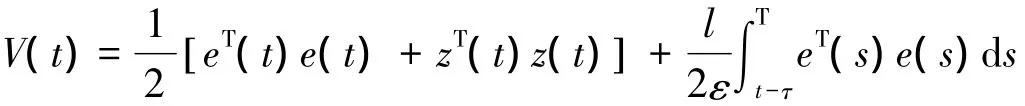
则

即

由引理2得

即

从定义1知系统( 2)指数同步于系统( 1)．注:由模型特点知，当e( t)指数趋于零时，z( t)也指数趋向零．

3仿真例子

考虑一个竞争性神经网络，其状态方程如式( 20) :

此时系统呈混沌现象(图1，图2)．根据定理1，可以验证误差系统指数趋于零(图3)．

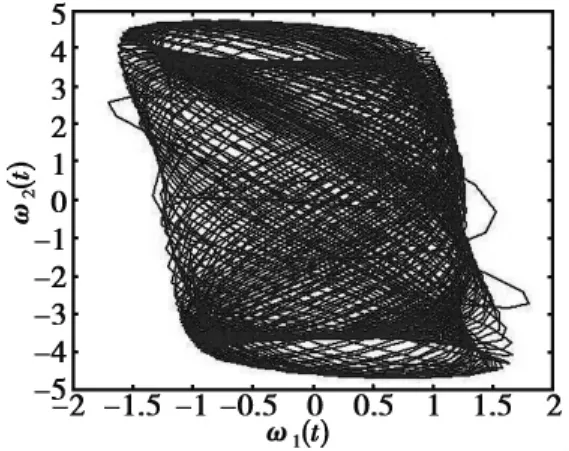
图1 x( t)的轨迹图

图2 S( t)的轨迹图

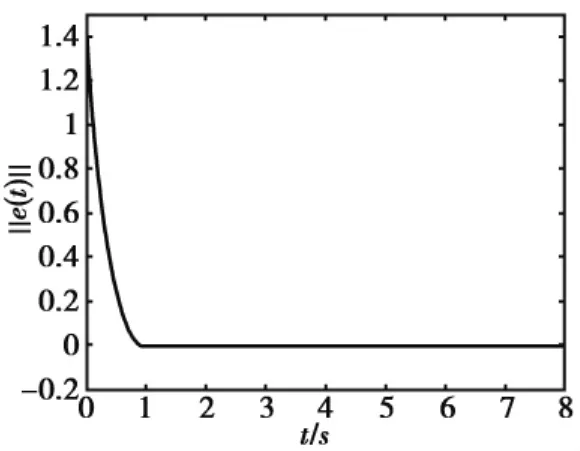
图3误差图

参考文献:

［1］MEYER-BASE A，PILYUGIN S，WISMUULLER A，et al．Local Exponential Stability of Competitive Neural Networks with Different Time Scale［J］．Engineering Applications of Artificial Intelligence，2004，17( 3) : 227-232

［2］YANG X，CAO J，LONG Y，et al．Adaptive Lay Synchronization for Competitive Neural Networks with Mixed Delays and Uncertain Hybrid Perturbations［J］．IEEE Trans Neural Networks，2010，21( 10) : 1656-1667

［3］GAN Q，HU R，LIANG Y．Adaptive Synchronization for Stochastic Competitive Neural Networks with Mixed Time-varying Delays ［J］．Communications in Nonlinear Science Numerical Simulation，2012，17( 9) : 3708-3718

［4］YANG X，CAO J．Exponential Synchronization of Delayed Neural Networks with Discontinuous Activations［J］．IEEE Circuits and Systems Society，2013，60( 9) : 2431-2439

［5］XIONG W，XIE W，CAO J．Adaptive Exponential Synchronization of Delayed Chaotic Networks［J］．Physica A: Statistical Mechanics and its Applications，2006( 2) : 832-842

［6］MA Z，ZHOU Y．Qualitative and Stability Method for Ordinary Differential Equation［M］．Science press，Bieijing，china，2001

Exponential Synchronization of Delayed Competitive Neural Networks
with Nonlinear Perturbations

SU Ting-ting

( College of Mathematics Science，Chongqing Normal University，Chongqing，401331 China)

Abstract:This paper researches the exponential synchronization of delayed competitive neural networks with nonlinear perturbations．Based on Lyapunov stability theory，inequality techniques，etc．，a simple controller is designed，and some sufficient conditions are obtained．The results of this paper are simpler and more practical and can be generalized to other neural networks．A numerical simulation is given to demonstrate the effectiveness of the results．

Key words:competitive neural networks; exponential synchronization; nonlinear perturbations; time delay

作者简介:苏婷婷( 1988-)，女，陕西宝鸡人，硕士研究生，从事同步与控制研究．

收稿日期:2014－10－09;修回日期: 2014－12－16．

doi:10．16055/j．issn．1672－058X．2015．0005．003

中图分类号:O232

文献标识码:A

文章编号:1672－058X( 2015) 05－0009－04