含有时滞的不连续神经网络在非线性干扰下的指数同步

艾霜

(重庆师范大学数学学院，重庆401331)



含有时滞的不连续神经网络在非线性干扰下的指数同步

艾霜

(重庆师范大学数学学院，重庆401331)

摘要:证明了一类含有时滞的不连续神经网络在非线性干扰下的指数同步．在一个反馈控制器下，得到了指数同步的结果;根据Lyapunov稳定性理论、Filippov解的定义，选取一个适合的Lyapunov函数，得到了一些证明指数同步的充分条件．

关键词:不连续神经网络;随机同步;时滞;非线性干扰

近年来，不连续神经网络的同步研究引起了广大专家学者的关注［1－3］．在文献［4］中，作者证明了一类不连续神经网络在一类状态反馈控制器下可以实现拟同步，也就是说误差系统可以被控制在零点很小的一个邻域内，但是不能到达零．但是不连续神经网路在现实生活中的应用往往被要求达到完全同步．例如，当不连续神经网络应用到保密通信时，只有驱动系统和响应系统实现完全同步，信号才可以被识别．与此同时，由于信号的传输通道拥挤或是受传输速度的影响，神经网络的时滞总是不可避免的，含有时滞的神经网络也被广泛关注．在文献［5］中，研究了一类含有时滞的竞争性神经网络的自适应同步．然而，在实际应用中，驱动响应的混沌系统总是处于各种不同的环境中，并且容易受到外部的干扰．基于以上分析，此处研究了一类含有时滞和非线性干扰的不连续神经网络的指数完全同步问题．

1模型介绍和准备工作

考虑一类含有相同结点和随机干扰的时滞不连续驱动响应神经网络:

U( t) = ( u1( t)，u2( t)，…，un( t) )T代表设计的反馈控制器，x( t) = ( x1( t)，x2( t)，…，xn( t) )TRn和y( t) = ( y1( t)，y2( t)，…，yn( t) )TRn代表神经网络的状态向量，f(·) ( i= 1，2，…，n)代表不连续的激励函数，A=( aij)n×nRn×n和B = ( bij)n×nRn×n分别代表不含时滞的加权矩阵和含有时滞的加权矩阵，x( t)和y( t)分别代表未知的非线性干扰，J=( J1，J2，…，Jn)代表外部输入向量．

假设1除了由孤立点ρik组成的可数个集合外，fi: R→R( i=1，2，…，n)都是连续的，其中右极限和左极限f－i(ρik)都存在;并且在每一个紧区间R中，fi至少有有限个不连续跳跃点．

假设2存在非负常数Li和pi，使得supi－i≤Liu－v+pi，u，vR，其中，iK［fi( u)］，

引理1 若ε＞0，对于任意的x，y ∈Rn，矩阵A∈Rn×n，有不等式( 3) 成立:

引理2( Halanay不等式)如果V( t)在［－τ，+)上是一个非负函数，τ≥0，且满足( t)≤－aV( t) + b( supt－τ≤s≤tV( s) )，t≥0，其中a＞b＞0，则有V( t)≤( sup－τ≤s≤0V( s) ) exp(－ρt)，t≥0，其中ρ是方程ρ= abexp(ρt)唯一的正解．

由于f(·)在Rn上是不连续的，因此系统( 1)和系统( 2)变为右端不连续的微分方程，并且它们的解在惯用的意义下是不存在的．所以，利用Filippov解意义下的集值映射来讨论系统( 1)和系统( 2)的动力学行为．

定义1［6］函数x:［－τ，T)→Rn，T( 0，+)被称作系统( 1)在［－τ，T)上的Filippov解，如果满足

( 1) x在［－τ，T)上是连续的，在［0，T)是绝对连续的;

( 2)存在一个可测函数γ( t) = (γ1( t)，γ2( t)，…，γn( t) )T:［－τ，T)→Rn，使得对于任意的t［－τ，T)，有γ( t)K( f( x( t) ) )，并且( t) =－x( t) +Aγ( t) +Bγ( t－τ( t) ) +x( t) +J，t［0，T)．

引理3［7］(链式法则)如果V( x) : Rn→R是C正则的，并且x( t)在［0，+)上的任意紧区间是绝对连续的，那么x( t)和V( x( t) ) :［0，+)→R在t［0，+)是可微的，并且，对于任意的γ( t)V( x( t) )成立，其中V( x( t) )是V在x( t)上的Clarke广义梯度．

由定义1和引理3将系统( 1)和系统( 2)分别表示为

令e( t) = y( t)－x( t)，式( 5)与式( 4)作差，得到误差系统:

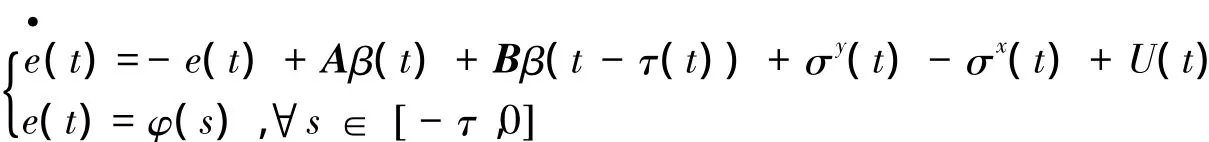
定义2如果存在常数M≥1，ρ＞0，使得e( t)2≤Msup－τ≤s≤0( s)2exp(－ρt)，t≥0，则称系统( 1)与系统( 2)达到指数同步．

2指数同步的证明

通过以上的分析，将证明系统( 1)和系统( 2)的指数同步转化为证明误差系统的指数稳定性．下面将证明误差系统在所给出的控制器下实现指数稳定．首先给出控制器U( t)，并且当e( t) = 0时，控制器满足U( t) = 0，U( t) =－Ke( t)－ηsign( e( t) )，其中K和η为正定的对角矩阵．

定理1若假设1－假设3是满足的，系统( 2)与系统( 1)在控制器U( t)下可以实现指数同步，如果满足条件( 6) :

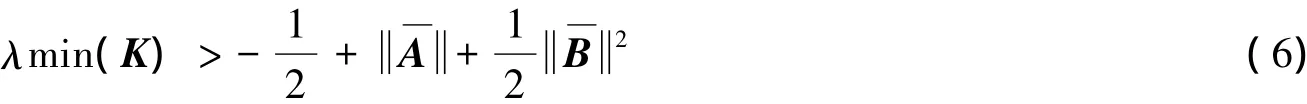
证明选取如下的Lyapunov函数:

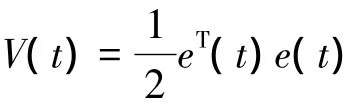
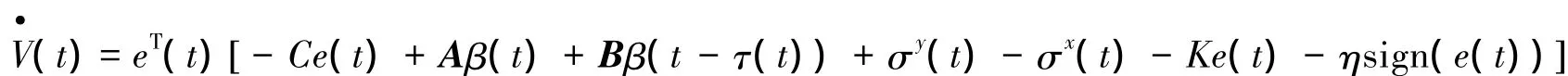
由假设1－假设3和引理1，得

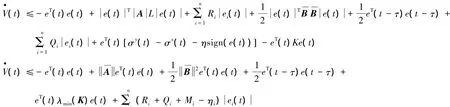
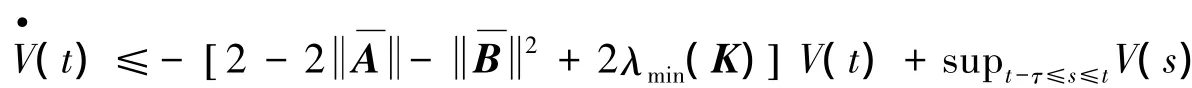
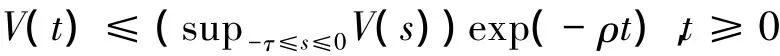
ρ是方程( 7)的唯一正解．

由定义2，神经网络( 1)和( 2)实现全局指数同步．证毕．

参考文献:

［1］QIN S，XUE X，WANG P．Global Exponential Stability of Almost Peiodic Solution of Delayed Neural Networks with Discontinuous Activations［J］．Information Sciences，2013( 220) : 367-378

［2］SHEN J，CAO J．Finite-time Synchronization of Coupled Neural Networks via Discontinuous Controllers［J］．Cognitive Neurody namics，2011( 5) : 373-385

［3］CHEN G，ZHOU J．Global Synchronization of Coupled Delayed Neural Networks and Applications to Chaotic CNN Models［J］．International Journal of Bifurcation and Chaos，2004( 14) : 2229-2240

［4］LIU X，CHEN T，CAO J，et al．Dissipativity and Quasi-synchronization for Neural Networks with Discontinuous Activations and Parameter Mismatches［J］．Neural Netwoks，2011( 24) : 1013-1021

［5］YANG X，CAO J．Adaptive Lag Synchronization for Competitive Neural Networks with Mixed Delays and Nncerta in Hybrid Perturbation［J］．IEEE Transactions on neural networks，2010，21( 10) : 1656-1667

［6］FORTI M，NISTRI P．Global Convergence of Neural Networks with Discontinuous Neuron Activations［J］．IEEE Transacyions on Circuits and Systems I: Fundamental Theory and Applications，2003( 50) : 1421-1435

［7］CLARKE F H．Optimization and Nonsmooth Analysis［J］．Society for Industrial Mathematics，1987( 5) : 385-390

Exponential Synchronization of Delayed Neural Networks with Discontinuous Activations and Nolinear Perturbations

AI Shuang

( College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

Abstract:This paper proves exponential synchronization of delayed neural network with discontinuous activations and nolinear perturbations．Exponential synchronization result is obtained under a state feedback controller．Based on Lyapunov stability property，under the framework of Filippov solution，by using a suitable Lyapunov function，some sufficient conditions of exponential synchronization are obtained．

Key words:discontinuous neural network; stochastic synchronization; time-delay; nonlinear perturbations．

作者简介:艾霜( 1989-)，女，重庆合川人，硕士研究生，从事混沌同步与控制研究．

收稿日期:2014－10－09;修回日期: 2014－11－16．

doi:10．16055/j．issn．1672－058X．2015．0005．002

中图分类号:O232

文献标识码:A

文章编号:1672－058X( 2015) 05－0006－03