等幂和问题的对称理想参数解

邱敏

(西南大学数学与统计学院，重庆400715)



等幂和问题的对称理想参数解

邱敏

(西南大学数学与统计学院，重庆400715)

摘要:介绍了等幂和问题的一些研究历史，给出了等幂和问题在n = 4，5，6时的对称理想解的参数形式．

关键词:等幂和问题;理想解;参数解

1研究背景介绍

关于等幂和问题的研究已经有两百多年的历史了［1］，在1750－1751年，Euler和Goldbach注意到，［a，b，c，abc］=2［a+b，a+c，b+c］．一个世纪后，1851年，Prouhet发现有nk+1个整数可以分成n个集合，使得每对集合恰好是长度为nk，度数为k的一个解，但Prouhet的结果一直没被关注．等幂和问题也被称为Tarry-Escott problem，直到Wright在文献［2］中提出Prouhet的贡献之后，该问题被称为Prouhet-Tarry-Escott problem．等幂和问题从代数和分析两个方面来看非常有趣，而其中理想解的讨论因其与计算机科学理论及组合学［3］中问题的联系又显得格外有趣．

Wright在1934年猜想:对所有的正整数n，总可以找到一个长度为n的理想解．但这个猜想并没有被证明．对n=2，3，4，5，全部的参数解已经找到了; n=6，7，8的部分参数解也找到了; n= 9时，只有两个不等价解被发现; n=10时，无限组不等价解也找到了;到2008年时也只有两组n=12的不等价解，n= 11和n≥13还没有理想解被发现．

等幂和问题是一个经典的丢番图方程，所谓“等幂和”，即给定自然数n，k，k＜n，找到整数集Z的两个不同子集［1，2，…，n］，［1，2，…，n］，使得对j=1，2，…，k，有，即

除了从方程的角度来研究等幂和之外，也可以从多项式的角度研究它．

定理1［4］由牛顿公式可得3个命题等价:

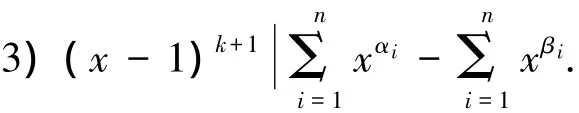
其中，由定理1命题3)可知，等幂和问题也可从多项式的角度来定义，即找到一个整系数多项式F( x)，使得F( x)的长度最小且能被( x－1)k+1整除．

推论1［4］由定理1可得，以下3个命题等价:

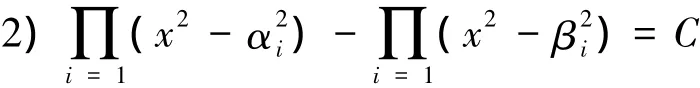
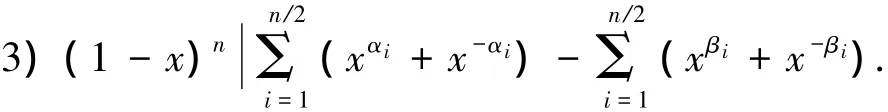
推论2［4］由定理1可得，以下3个命题等价:

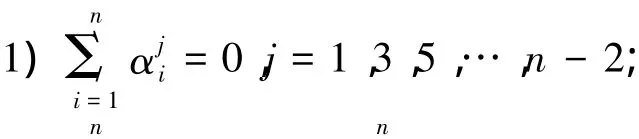
由等幂和问题的定义可知，一个解可以生成一组解，即

引理1［4］若［1，2，…，n］，［1，2，…，n］是一个次数为k的解，则［M1+K，M2+K，…，Mn+K］，［M1+K，M2+K，…，Mn+K］也是一个次数为k的解，其中M，K为任意常数，称这样的两个解为等价解．

对给定的n，可以由次数为k的解构造一个次数为k+1的解．即

引理2［4］若［1，2，…，n］，［1，2，…，n］是一个次数为k的解，则［1，2，…，n，1+h，2+h，…，n+h］，［1+h，2+h，…，n+h，1，2，…，n］是一个次数为k+1的解，其中h为任意常数．

2等幂和问题的对称理想参数解

Jack Chernick在文献［5］中给出了长度n = 2，3，…，8的对称参数解，此处在此基础上，给出了寻找n=4，5，6时的对称理想解的另一种方法，并根据这种方法得出了一些不同的参数解．在以下讨论中，a，b为任意的整数．

由推论2可知，长度为3的对称理想解可以由方程x1+x2+x3=0给出，该方程的二阶齐次参数解可以表示为x1=－a，x2=－b，x3=a+b，则［a+b，－a，－b］=2［－( a+b)，a，b］为n=3的一个对称理想参数解．

由引理2及n=3的对称理想解的参数形式可得

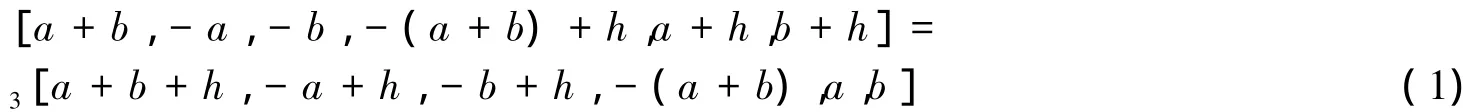
取h=a－b，则式( 1)可化为

对式( 2)应用引理1，取M=2，K=－( a－b)，得

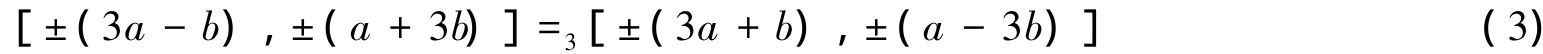
即式( 3)是长度为4的一个二阶齐次对称理想参数解．

同样由引理2可得

取h=－2ab－2，则式( 5)可化为

若在式( 5)中取－ab－a－b+1=－ab+a+b－3，则b=－a+2，式( 6)可化为

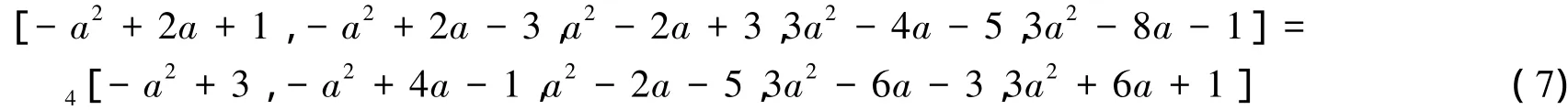
对式( 7)应用引理1，取M=1/2，K=－( a2－2a－1) /2，得

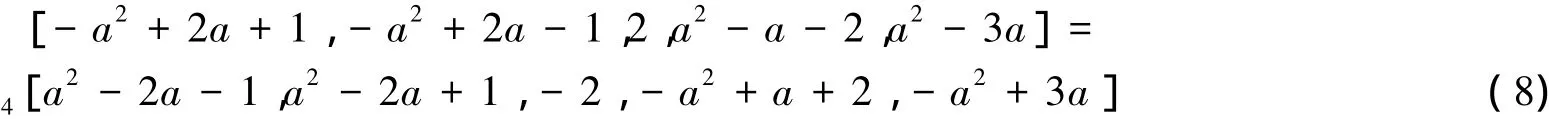
则式( 8)是长度为5的一个一阶非齐次对称理想参数解，且由式( 8)，可以生成一个长度为5的二阶齐次对称理想参数解:

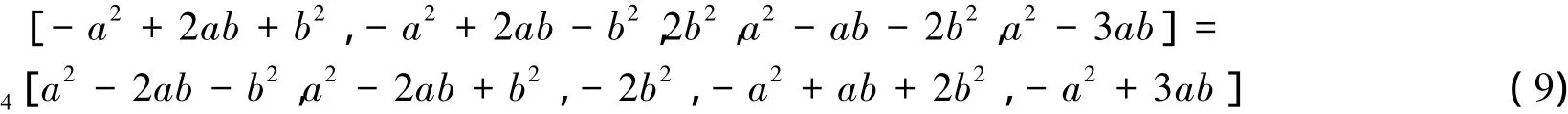
若在式( 5)中取－3ab+a－b－3=ab－a+b+1，则b=( a－1) /( 2a+1)，式( 6)等价于

对式( 10)应用引理1，取M=( 2a+1) /2，K=( a2+1) /2得

式( 11)是长度为5的一个对称理想参数解，且由式( 11)，可以生成一个长度为5的二阶齐次对称理想参数解:

对式( 12)再应用引理2及引理1，取h=－2a2－2ab+2b2，M=1，K=a2+ab－b2，则式( 12)可化为

即式( 13)是长度为6的一个二阶齐次对称理想参数解．

参考文献:

［1］BORWEIN P．Computational Excursions in Analysis and Number Theory［M］．New York: Springer－Verlag，2002

［2］WRIGHT E M．Prouhet’s 1851 Solution of the Tarry－Escott Problem of 1910［J］．Amer Math Monthly，1959( 66) : 199-201

［3］陈景润，黎鉴愚．关于等幂和问题［J］．科学通报，1985，30( 4) : 316-317

［4］BORWEIN P，INGALLS C．The Prouhet-Tarry-Escott Problem Revisited［J］．Enseign，Math，1994( 40) : 3-27

［5］CHERNICK J．Ideal Solutions of the Tarry－Escott Problem［J］．Amer Math Monthly，1937( 44) : 626-633

The Symmetric Ideal Parametric Solutions to the Prouhet-Tarry-Escott Problem

QIU Min

( College of Mathematics and Statistics，Southwestern University，Chongqing 400715，China)

Abstract:This paper introduces the research history of Prouhet-Tarry-Escott problem，and gives parametric form of the symmetric ideal solutions when n=4，5，6 in the Prouhet-Tarry-Escott Problem

Key words:Prouhet-Tarry-Escott problem; ideal solutions; parametric solutions

作者简介:邱敏( 1991-)，女，四川遂宁人，硕士研究生，从事计算数论研究．

收稿日期:2014－09－16;修回日期: 2014－10－16．

doi:10．16055/j．issn．1672－058X．2015．0005．012

中图分类号:O156．2

文献标志码:A

文章编号:1672－058X( 2015) 05－0040－03