有理数域上一类不可约多项式的简单推广

黎智

(重庆师范大学数学学院，重庆401331)



有理数域上一类不可约多项式的简单推广

黎智

(重庆师范大学数学学院，重庆401331)

摘要:若a1，a2，…，an是n－1个不同的整数，证明了当n≥4时，f( x) = ( x－a1) ( x－a2)…( x－an)－1在有理数域Q上不可约;当n≥3时，f( x) = ( x－a1)2( x－a2)2…( x－an)2+1在有理数域Q上不可约．

关键词:有理数域;多项式;不可约;系数;次数

有理系数多项式、整系数多项式是数论研究的重要类容，研究数域上的不可约多项式就好比研究整数中的素数一样重要．在代数中已经证明如果一个非零的整系数多项式能够分解成两个次数较低的有理系数多项式的乘积，那么它一定能分解成两个次数较低的整系数多项式的乘积．也就是说，在Z上不可约的整系数多项式，在Q上也不可约．因此，关于有理数域上多项式的可约性问题，可以简化为讨论整系数多项式在整数环上的可约性问题．而判别一个整系数多项式是否可约，常常是困难的．在这方面比较著名的方法有以下几类:

Ⅰ通过多项式的系数和某素数的整除关系来判定不可约，如Eisenstein判别法及其推广形式［1－2］．

Ⅱ通过比较多项式系数的大小来判别不可约，如Perron判别法及其改进形式［3－4］．

Ⅲ通过计算f( x)在Z上的取值来判别不可约，如命题1．

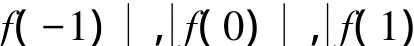
Ⅳ通过辅助多项式根的取值来判别不可约，如命题2．

命题2［3］设a1，a2，…，an是彼此不相同的整数，则

1) f( x) = ( x－a1) ( x－a2)…( x－an)－1在有理数域Q上不可约;

2) f( x) = ( x－a1)2( x－a2)2…( x－an)2+1在有理数域Q上不可约．

定理及其证明如下:

命题2实则是Schur本世纪初提出的两个简单问题，已经得到了证明，此处在此基础上做了一个简单的推广，主要结果是:

定理1设a1，a2，…，an是n－1个不同的整数，则

1)当n≥4时，f( x) = ( x－a1) ( x－a2)…( x－an)－1在有理数域Q上不可约;

2)当n≥3时，f( x) = ( x－a1)2( x－a2)2…( x－an)2+1在有理数域Q上不可约．

证明1)不妨设an=a1，则f( x) = ( x－a1)2( x－a2)…( x－an－1)－1．若f( x)在Q上可约，可设f( x) = f1( x) f2( x)，fi( x)是整系数多项式; 1≤°( fi( x) )＜n( i = 1，2)，其中，( f( x) )表示f( x)的次数，由于f( ai) =－1，i= 1，2，…，n，故f1( ai) =±1，f2( ai) =1，i= 1，2，…，n，即f1( ai) +f2( ai) = 0，i= 1，2，…，n．若f1( x) +f2( x)的次数小于n－1，则f1( x) +f2( x) = 0，即f1( x) =－f2( x)，f( x) =－( x)，因为f( x)的最高项系数是1，此不可能．

故f1( x) +f2( x)的次数只能等于n－1．不妨令( f1( x) ) = n－1，则( f2( x) ) = 1，此不可能．因为根据文献［5］引理1的证明可知，当n≥4时，即n－1≥3，对于任何整数x'，要么( x'－a1)2( x'－a2)…( x'－an－1) = 0，要么式，与( f2( x) ) = 1矛盾．

综上，当n≥4时，f( x) = ( x－a1) ( x－a2)…( x－an)－1在有理数域Q上不可约．

2)不妨设an=a1，则f( x) = ( x－a1)4( x－a2)2…( x－an－1)2+1．显然f( x)没有实根，若f( x)在Q上可约，类似1)可设f( x) = f1( x) f2( x)，fi( x)是整系数多项式，1≤( fi( x) )＜n( i=1，2)．因为对任意实数，f( x)＞0，不妨设对所有实数f1( x)＞0，f2( x)＞0，由于f( ai) = 1，i=1，2，…，n，故f1( ai) = f2( ai) = 1，i=1，2，…，n．若fi( x) ( i= 1，2)的次数小于n－1，则fi( x)≡1( i=1，2)，与所设不和，故只可能是以下两种情形:，所以f( x')≠0，因此f( x)没有一次有理因

或者

当n≥3时，对于式( 1)，可令

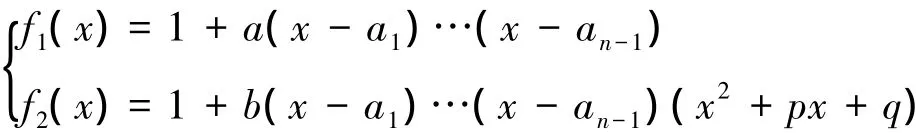
其中a，b，p，q为整数，由f( x) = f1( x) f2( x)可知

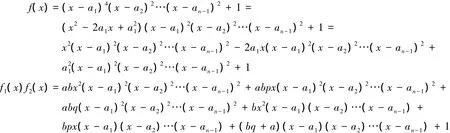
比较左右两端系数得

即

化简得( x－a1)2+1=0，此不可能．

对于式( 2)，类似式( 1)，可令

其中c，d，m，n为整数，由f( x) = f1( x) f2( x)可知

比较等式左右两边系数得

即

解得x=a1，与xai矛盾．

参考文献:

［1］王萼芳，石生明．高等代数［M］．3版．北京:高等教育出版社，2007

［2］赵敦，罗彦峰，雷鹏．Eisenstein判别法的一个推广［J］．高等理科教育，2005( 6) : 38-39

［3］柯召，孙琦．数论讲义(下)［M］．北京:高等教育出版社，1987

［4］王瑞．判定Q上多项式不可约的一种方法［J］．数学研究与评论，2002，22( 4) : 679-684

［5］张卫，史滋福．有理数域上的一类不可约多项式［J］．湖南理工学院学报:自然科学版，2008，21( 1) : 5-7

Simple Generalization of a Class of Irreducible Polynomials in Rational Number Field

LI Zhi

( College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China)

Abstract:Suppose a1，a2，…，anare different Integers of n－1．This paper proves that if n≥4，the polynomial f( x) = ( x－a1) ( x－a2)…( x－an)－1 is irreducible in the rational number range Q，and if n≥3，the polynomial f( x) = ( x－a1)2( x－a2)2…( x－an)2+1 is irreducible in the rational number range Q．

Key words:rational number field; irreducible polynomial; coefficients; degree

作者简介:黎智( 1990-)，男，重庆奉节人，硕士研究生，从事数论研究．

收稿日期:2014－06－18;修回日期: 2014－10－08．

doi:10．16055/j．issn．1672－058X．2015．0005．007

中图分类号:O156

文献标识码:A

文章编号:1672－058X( 2015) 05－0023－03