基于成像测井资料多种滤波方法在裂缝识别中的应用

王瑞雪, 张晓峰, 谈顺佳,2, 黄飘

(1.东华理工大学核工程与地球物理学院, 江西 南昌 330013; 2.中国地质科学院地质研究所, 北京 100037)

0 引 言

据不完全统计,世界上裂缝型油藏的储量约占已探明总储量的一半,因此对裂缝性储层的裂缝研究有极其重要的意义[1]。声、电成像测井方法已成为全球探测识别裂缝及层理最精确、最直观的方法,国内外很多学者[2-4]开始了对成像测井方法的研究,利用该方法识别裂缝、层理、岩性及进行地质解释等。成像测井虽然能够直观地反映裂缝存在,但在人机交互解释中存在着人为误差,而滤波方法可以增强储层中裂缝的信息,进而在一定程度上减小这种误差[5]。近年来,将测井资料与多种滤波方法相结合识别裂缝及层理、划分地层等的研究颇多。Lu P B等[6]提出用小波分析中的多分辨率分析评价储层参数;Isha Sahni等[7]提出用多分辨率小波分析理论对油藏描述进行改进;张小涛等[8]将二维小波变换与中值滤波相结合应用于FMI图像的去噪中,取得较好效果;张晓峰等[5,9]以常规测井及电成像测井资料为基础利用小波变换方法增强裂缝信息,并识别裂缝,取得较好的效果;陈波等[10]利用自适应中值滤波技术对声波测井数据进行处理,有效去除了信号中的脉冲噪声,提高了测井曲线的分辨率。张晓峰等[11]以裂缝密度为基础,通过对不同小波基的小波变换方法进行研究发现,在裂缝识别过程中,bior 4.4小波分解的高频信号信息与裂缝密度线性相关性最好。在此基础上,本文选取均值滤波、中值滤波及bior 4.4小波变换对裂缝进行滤波处理,3种滤波方法均可针对裂缝信息进行滤波,但其滤波效果不同。

本文以增强裂缝信息、提高裂缝识别精度为目的,针对裂缝识别滤波方法的选择问题展开研究,首先对电导率数据进行各种滤波处理,选取最佳的滤波方法及滤波窗口,并尝试利用surfer软件对滤波的电导率数据进行再次成图识别裂缝。

1 滤波原理

1.1 均值滤波原理

(1)

1.2 中值滤波原理

中值滤波器是一种非线性滤波器,其原理是选择合适的滑动窗口,将窗口内各点的中值作为基准,当前值和中值比较差别较大的认为是噪声进行滤除,否则给予保留[12]。若取窗口点数为一奇数m,其中值滤波就是从输入数据中抽取m个数据,并将这m个数据的值按大小进行排序,取其序号为中心点的那个数作为滤波输出,中值运算可表示为

(2)

式中,xi为数据序列;xm为中值;A为中值滤波窗口;v为滤波半径;Med为取中值运算。其滤波算法为

(3)

1.3 小波变换原理

小波变换方法是一种窗口大小固定、窗口形状可变、时间窗和频率窗都可改变的时频域局部化分析方法,很适合探测正常信号中突变信号的成分[13],其基本思想是将信号分解为一系列由某个母小波函数经过平移与尺度变化得到的小波函数的叠加,用不同尺度小波对同一信号进行逼近以利于对信号进行逐步细致的分析[14],具有数学显微镜的功能。将任意L2(R)空间中的函数z(t)在基小波下进行展开,任意函数z(t)的连续小波变换为[15]

(4)

式中,a和b分别代表尺度参数和平移参数;WTz(a,b)为小波变换系数;在本文研究中,z(t)为要进行小波变换的测井曲线;φ(t)为研究中所选的基小波函数。

2 滤波方法的选择

2.1 滤波质量评价方法

滤波方法可以有效滤除观测信号中的噪声,在进行滤波处理的过程中,需要根据信号的实际情况选择不同的滤波方法及滤波窗口。选择的滤波方法及滤波窗口不同,滤波后得到的结果就不同,即滤波效果也不同。因此,滤波方法及滤波窗口的选择则是滤波处理的关键。目前滤波质量评价指标主要有以下4种[16]。

2.1.1 均方根误差(RMSE)

均方根误差指滤波后的信号与原始信号的均方误差,记为RMSE,表达式为

(5)

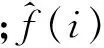
均方根误差体现了原始信号与滤波之后信号之间的差异,均方根误差越小表示滤波效果越好。

2.1.2 信噪比(SNR)

信噪比指原始信号能量与噪声能量的比值,记为SNR,表达式为

SNR=10×lg(Psignal/Pnoise)

(6)

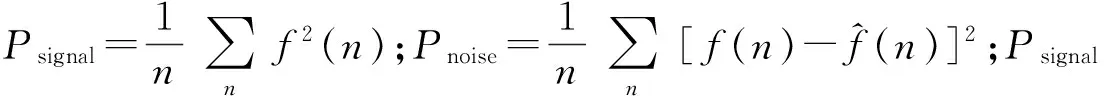
2.1.3 互相关系数(R)

互相关系数指小波滤波后的信号与理论参考信号的相似度,记为R,表达式为

R=Cov(xi,yi)/δxδy

(7)

式中,Cov(xi,yi)为xi和yi的协方差;δx、δy分别为xi、yi的标差。一般认为,R越接近1,则滤波效果越好。

2.1.4 平滑度指标(r)

平滑度指标指滤波后信号的差分数的方差根与原始信号的差分数的方差根之比,表达式为

(8)

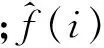
2.2 滤波质量指标与滤波窗口的对应关系

在各种滤波过程中,均值滤波及中值滤波的滤波窗口内数据个数n的大小将会直接影响滤波效果的好坏;bior 4.4小波变换滤波的分解、重构层数n也会对滤波效果产生影响。图1、图2分别为均值滤波、中值滤波的滤波窗口内数据个数与滤波指标计算值的关系图;图3为bior 4.4小波变换的分解重构层数与滤波指标计算值的关系图。

通过对图1、图2、图3中各种指标变化的分析,并结合滤波去噪质量评价指标的评价方法,可以发现,当均值滤波窗口内数据个数n=41时其滤波效果较好;当中值滤波窗口内数据个数n=40时其滤波效果较好;当bior 4.4小波变换的分解重构层数为n=4时其滤波效果较好。

2.3 最佳滤波方法选取

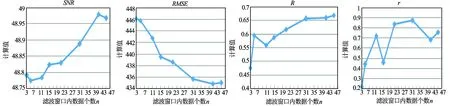
图1 均值滤波质量指标评价图

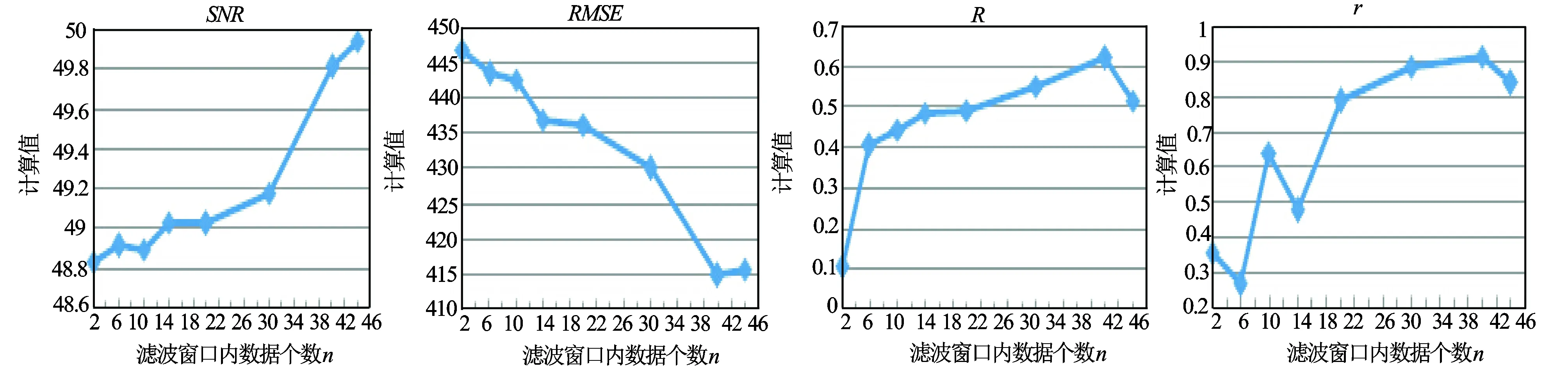
图2 中值滤波质量指标评价图

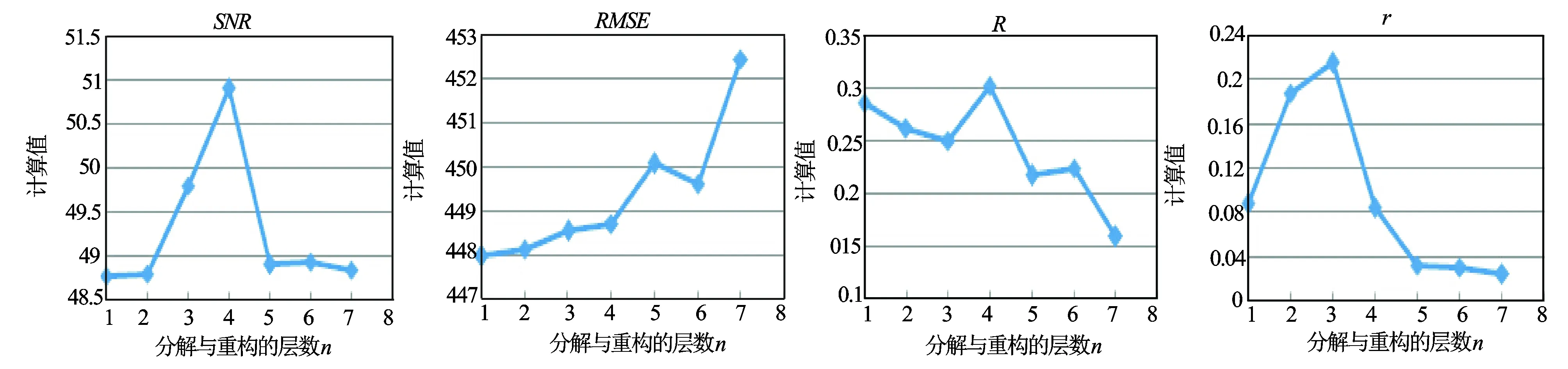
图3 bior 4.4小波变换滤波质量指标评价图

对川西的邛西A井3 267.80～3 268.80 m段的电导率数据分别进行均值滤波、中值滤波及bior 4.4小波变换滤波处理,并依据以上滤波质量评价方法对不同滤波方法滤波后的信号进行质量评价选取最佳滤波方法(见表1)。

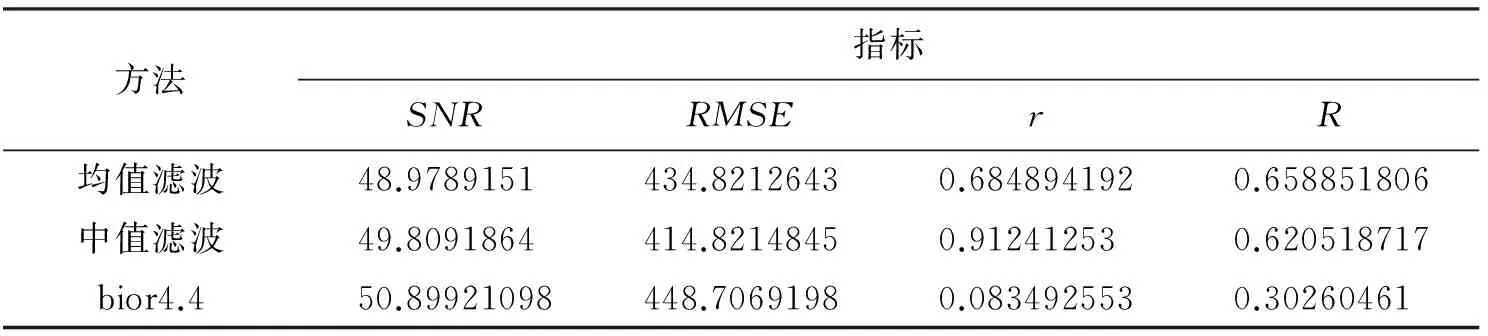
表1 不同滤波方法的滤波效果的评价对比表

由表1可知,指标SNR最大值对应的滤波方法为bior 4.4;指标RMSE最小值对应的滤波方法为中值滤波;指标r最小值对应的滤波方法为bior 4.4;指标R最大值对应的滤波方法为均值滤波。综合多评价项指标考虑,认为在电导率数据滤波识别裂缝的过程中,bior 4.4小波变换滤波方法为最佳滤波方法。

3 裂缝识别

对川西的邛西A井3 266.867～3 268.809 m段的电导率数据分别作均值滤波、中值滤波、bior 4.4小波变换滤波处理,将滤波的电导率数据导入surfer软件成图,依据电导率的变化识别裂缝,将多种滤波方法识别的裂缝与FMI成像测井识别的裂缝进行对比分析(见图4)。图4中第1道为深度,第2道为FMI成像测井图,第3道为均值滤波电导率成像图,第4道为中值滤波电导率成像图,第5道为bior 4.4小波变换电导率成像图。

在surfer软件成图过程中经过多次调试将均值滤波电导率值δ≥170、中值滤波电导率值δ≥180、bior4.4小波基滤波电导率值δ≥80的值域界定为为高导值,将高导区全部填充红色(见图4),红色部分即为裂缝发育区。

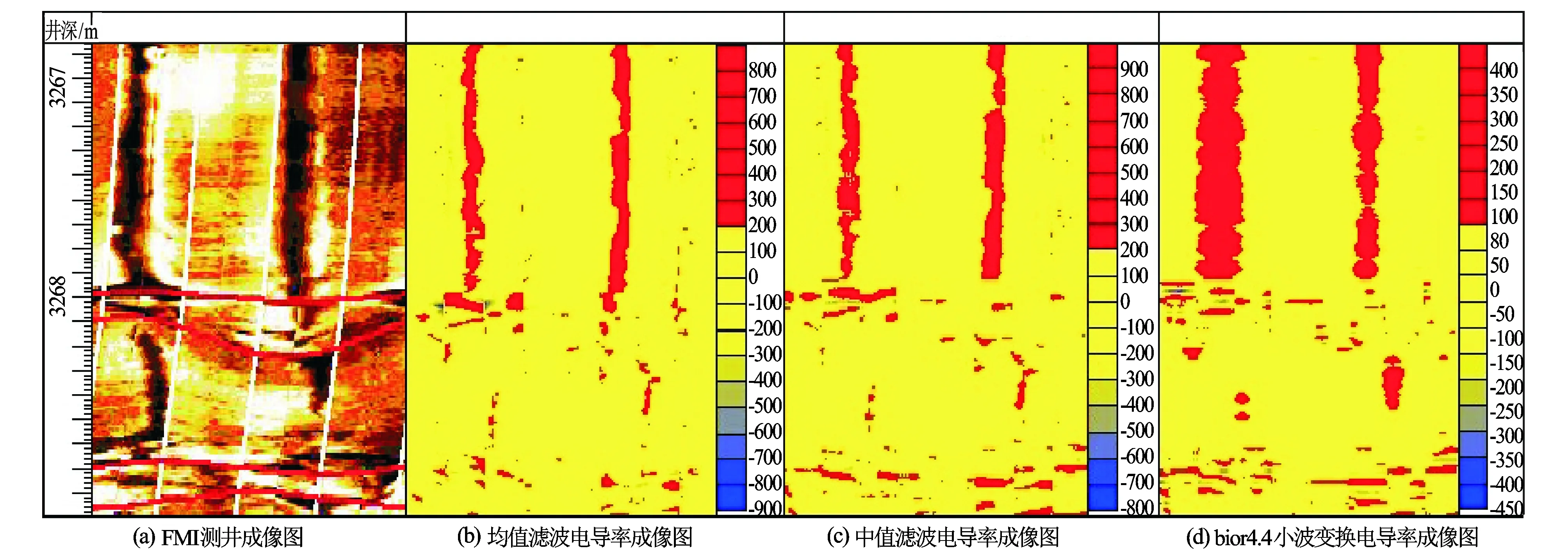
图4 裂缝识别对比图

从图4可见,均值滤波、中值滤波及bior 4.4小波变换滤波均能在不同程度上增强裂缝信息。其中,均值滤波图中所识别的裂缝清晰度较差,中值滤波及bior 4.4小波变换滤波图所识别的天然裂缝形态较清晰,而且所识别的裂缝位置与FMI测井成像图有较高的吻合度。通过对图4中所识别的裂缝信息量及诱导缝边界位置进行分析,可以看出,bior 4.4小波变换滤波图中所识别的裂缝信息较丰富,而且诱导缝的边界位置与FMI成像测井图中诱导缝的边界位置能更好地对应。

将4幅图中的诱导缝与天然裂缝进行综合对比分析可知,在电导率数据滤波识别裂缝的过程中,bior 4.4小波变换的滤波效果最好,该方法滤波后识别出的裂缝信息丰富,准确度更高,所识别的天然裂缝的正弦曲线形态明显,能够为成像测井的人机交互解释提供依据,有效提高裂缝识别精度。

4 结 论

(1) 电导率成像测井数据滤波识别裂缝的过程中,bior 4.4小波变换滤波效果要优于均值滤波及中值滤波,该滤波方法滤波过程中能更好地保留原始信号的突变部分或边缘信号,使得裂缝识别的准确度和精度更高。

(2) surfer软件再次成图识别的裂缝与FMI测井成像图识别的裂缝有较高的吻合度,可为成像测井的人机交互解释提供一定的参考依据,有效提高裂缝识别的准确度,为下一步计算机自动识别裂缝的研究提供基础。

(3) 小波变换过程中小波基及小波变换分解与重构层数的选择是关键。不同的小波基及不同的分解重构层数其滤波效果不同,滤波质量的好坏将直接影响裂缝的识别精度。

(4) 均值滤波及中值滤波过程中,滤波窗口的选择是关键。通常滤波窗口越大平滑效果越好,但信号的边缘和细节部分会变得模糊,在实际应用过程中需要根据不同的信号来选择不同的滤波窗口。

参考文献:

[1] 汪必峰. 储集层构造裂缝描述定量预测 [D]. 北京: 中国石油大学, 2007.

[2] 王珺, 杨长春, 等. 微电阻率扫描成像测井方法应用及发展前景 [J]. 地球物理学进展, 2005, 20(2): 357-364.

[3] 师玉璞. 成像测井地质解释系统 [D]. 西安: 西安科技大学, 2011.

[4] 吴煜宇, 张为民, 田昌炳, 等. 成像测井资料在礁滩型碳酸盐岩储集层岩性和沉积相识别中的应用——以伊拉克鲁迈拉油田为例 [J]. 地球物理学进展, 2013, 28(3): 1497-1506.

[5] 张晓峰, 潘保芝. 二维小波变换在成像测井识别裂缝中的应用 [J]. 石油地球物理勘探, 2012, 47(1): 173-176.

[6] Lu P B, Horne R N. A Multi-resolution Approach to Reservoir Parameter Estimation Using Wavelet Analysis [C]∥SPE 62985, 2000.

[7] Isha Sahni, Horne R N. Multi-resolution Wavelet Analysis for Improved Reservoir Description [C]∥SPE Reservoir Evaluation & Engineering. 2005: 53-69.

[8] 张小涛, 张烈辉, 冯国庆, 等. 基于小波变换和中值滤波的FMI信号去噪方法 [J]. 钻采工艺, 2009, 32(4): 51-54.

[9] Zhang Xiaofeng, Pan Baozhi, et al. A Study of Wavelet Transforms Applied for Fracture Identification and Fracture Density Evaluation [J]. Applied Geophysics. 2011: 164-169.

[10] 陈波, 梁永瑜, 胡敏, 等. 自适应中值滤波技术在测井数据处理中的应用 [J]. 复杂油气藏, 2013, 6(2): 23-25.

[11] ZhangXiaofeng, Wang Ruixue, et al. Wavelet Selection of Conventional Logging Curve Based on the Fracture Density [C]∥Near-surface Geophysics and Urbanization, ICEEG2014, Xi’an, USA: Zuoshu Pan, 2014: 687-691.

[12] 张江辉, 陈翠华, 宁全利, 等. 几种滤波在数据自动平滑处理中的对比分析 [J]. 四川兵工学报, 2013, 34(4): 101-103.

[13] 苟量, 彭真明. 小波多尺度边缘检测及其在裂缝预测中的应用 [J]. 石油地球物理勘探, 2005, 40(3): 309-313.

[14] 刘志松. 基于小波分析的信号去噪方法 [J]. 浙江海洋学院学报: 自然科学版, 2011, 30(2): 150-154.

[15] 葛哲学, 陈仲生. Matlab时频分析技术及其应用 [M]. 北京: 人民邮电出版社, 2006: 1-10.

[16] 陶柯. 小波去噪质量评价方法研究 [D]. 长沙: 中南大学, 2012.