压力载荷对声波测井圆管换能器影响有限元分析

曹雪砷, 王易敏 ,王申

(1. 中国石油集团测井有限公司, 陕西 西安 710077;2. 大庆钻探工程公司地质录井一公司, 黑龙江 大庆 163001)

0 引 言

声波换能器的性能直接影响测井效果。经过半个多世纪的发展,声波测井换能器已经由最初的单极子,逐步发展为偶极子、四极子,以满足不同地层条件下的测井需求[1-2]。井下的单极子采用圆管状结构的压电振子,其在沿径向膨胀和收缩的振动过程中始终保持圆管的对称外形不变[3-4]。圆管换能器在仪器装配过程中,需钳紧固定,机械边界条件对换能器的频率响应及发射性能均有影响。在设计、装配声波仪器时需要考虑单极子换能器的固定状态,使其满足现场所需要的频率特征和发射特性。有限元法是解决许多复杂物理问题的有效方法,ANSYS有限元分析软件可以解决结构、力学、热学、流体、电磁场以及任意2种以上物理场之间耦合等物理问题[5-7]。本文通过ANSYS对声波测井径向极化圆管换能器在空气以及流体中不同压力条件下的振动模态、频率响应以及发射响应进行分析,并分析了理论结果在声波测井技术中的应用。

1 圆管换能器的有限元仿真

1.1 圆管换能器的有限元模型

圆管换能器采用径向极化的极化方式,在周向上完全对称。装配后的圆管换能器上下各有一个金属挡板,换能器中心穿过一个两端带有螺纹的金属轴,金属轴穿过金属挡板后由挡板锁紧螺母将金属挡板压紧。螺母旋入多少不同,则挡板对换能器的压力不同。本文主要研究两端压力对换能器的影响,因此将模型简化,在换能器两端加载压力载荷,用以模拟金属挡板夹持换能器的松紧状态(见图1)。

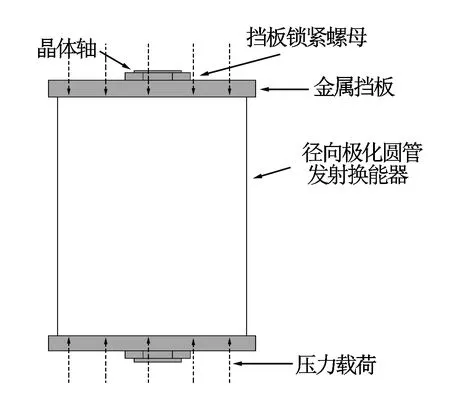
图1 圆管换能器装配示意图

利用ANSYS分别建立换能器在空气和水中的有限元模型。圆管内径52 mm,外径62 mm,高76 mm。采用实体单元类型SOLID5,压电陶瓷材料选用PZT5A,沿x轴方向极化,材料参数分别如式(1)至式(3)所示,密度7 500 kg/m3[见图2(a)][8]。在水中的情况下,换能器周向对称,可以采用平面轴对称单元类型PLANE13建立1/4有限元模型以节省内存资源和提高计算速度。在换能器外用对称单元类型PLANE13建立1/4圆的流体模型,半径0.5 m,密度1 000 kg/m3,声速1 500 m/s,外边界圆弧定义吸收边界,换能器辐射面加流体—结构耦合边界条件[5][见图2(b)]。

[C]=

(1)

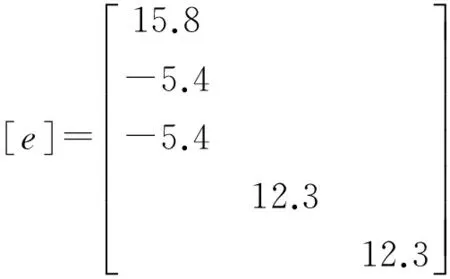
(2)

(3)

式中,C为刚度矩阵,N/m2;e为压电参数矩阵,N/V·m;ε为介电参数矩阵,C/m。

图2 圆管换能器的有限元模型

1.2 不同压力载荷下换能器的振动模态分析

ANSYS模态分析器能够提取换能器各阶模态的谐振频率[6-7]。分别对换能器在两端施加0(自由状态)、500、1 000、5 000、10 000、15 000 MPa等6个压力载荷情况下进行预应力模态分析。预应力模态分析分为2步,首先在加载压力载荷的情况下进行静力分析,再利用静力分析的结果进行模态分析。分别将换能器内外两面所有节点各定义一个耦合部,定义同一耦合部自由度耦合的节点处于等势状态,分别加载0 V和1 V的电压,模态分析选择BLOCK LANZOCS法,得到不同压力载荷下换能器在0～30 kHz频段内的振动模态的谐振频率(见表1)。由表1中可以看出,随着压力的增加,各阶模态的谐振频率降低,且当压力增加到一定数值,有的模态将会消失。自由状态下换能器各阶振动模式位移矢量剖面图如图3所示,压力为15 000 MPa时换能器各阶振动模式位移矢量剖面图如图4所示。对比图3及图4可以看出,当压力为15 000 MPa时,换能器在0～30 kHz频段内只余4阶振动模态,振动模态已经与自由状态下差异较大,原有的振动模式消失,产生了新的振动模式。

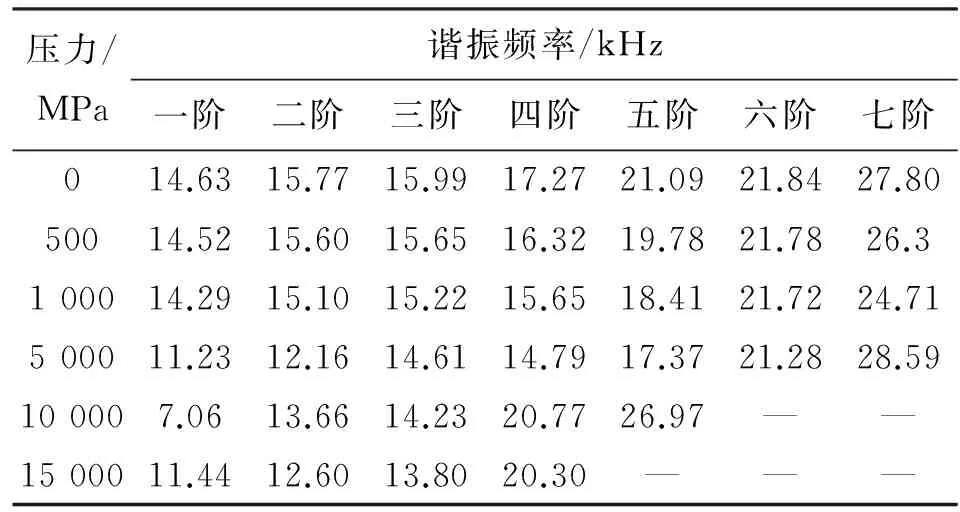
表1 不同压力下各振动模态的谐振频率

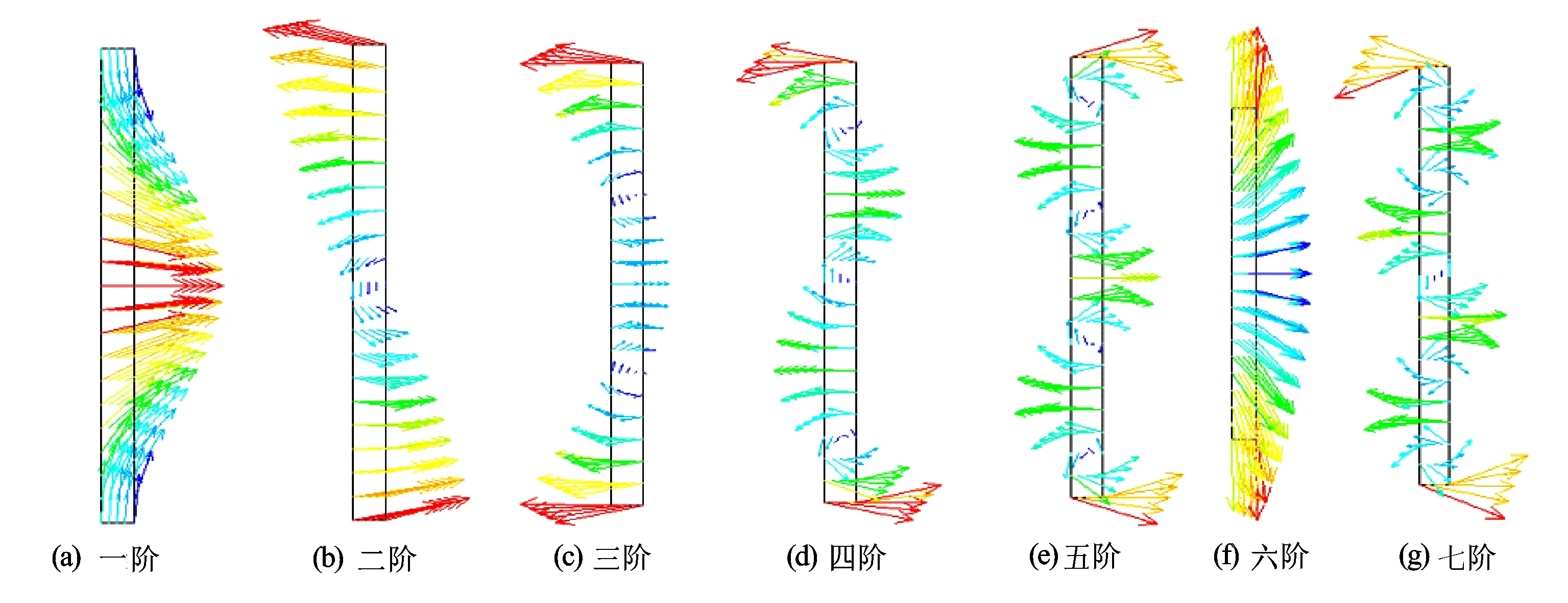
图3 自由状态换能器振动模式位移矢量剖面图

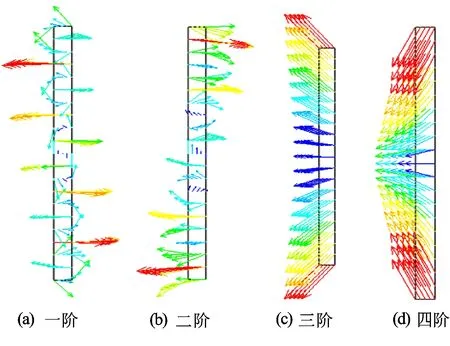
图4 15 000 MPa压力下换能器振动模式位移矢量剖面图

1.3 不同压力载荷下换能器在空气中的频响特性

ANSYS谐波分析器用于求解线性结构承受随时间正弦规律变化载荷的稳态响应[5],由此可以得到换能器导纳曲线、发射电压响应曲线等重要参数。对空气中圆管换能器进行谐响应分析时,分别将换能器内外两面所有节点各定义一个耦合部,定义同一耦合部自由度耦合的节点处于等势状态,分别加载0 V和1 V的电压,求解后可得到换能器的导纳特性曲线。

分别对换能器在两端施加0、500、1 000、5 000、10 000、15 000 MPa等6种压力载荷情况下进行预应力谐响应分析,扫频范围8～30 kHz,子步设为500步,得到换能器在6种情况下的空气中电导和电纳曲线(见图5)。从图5中可以看出,换能器在自由状态下有14.64、16.01以及21.82 kHz的3个谐振点,分别对应换能器振动的第1、第3和第6阶模态。不同压力下换能器谐振频率及对应的电导值如表2所示,随着压力的增加,21.82 kHz处谐振点频率逐渐降低,对应的电导值逐渐升高;16.01 kHz处谐振点频率逐渐降低,电导值逐渐升高;14.64 kHz处谐振点频率逐渐降低,电导值逐渐降低。当压力为5 000 MPa时,换能器只剩2个谐振点,随着压力继续增加,低频处谐振点频率降低,电导值继续下降,当压力为15 000 MPa时完全消失,此时换能器只剩1个谐振点,对应换能器振动的第4阶模态。

1.4 不同压力载荷下换能器在水中的频响特性

对水中圆管换能器进行谐响应分析时,同样分别将换能器内外两面所有节点各定义一个耦合部,分别加载0 V和1 V的电压,定义阻尼系数为0.042,求解后可得到换能器的导纳特性曲线和发射电压响应曲线。分别对换能器在两端施加0、500、1 000、5 000、10 000、 15 000 MPa压力载荷等6种情况下进行预应力谐响应分析,谐响应分析扫频范围8～30 kHz,子步设为500步,得到换能器在6种情况下的水中电导和电纳曲线(见图6)。不同压力下换能器谐振频率及对应的电导值如表3所示。由表3可以看出,换能器在自由状态下有14.42 kHz和21.46 kHz的2个谐振点,随着压力的升高, 高频处谐振点频率逐渐降低,电导值逐渐降低;低频处谐振点频率逐渐降低,电导值逐渐降低,当压力为15 000 MPa时完全消失,此时换能器只剩1个谐振点。

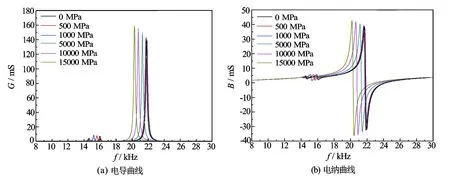
图5 换能器在空气中不同压力下导纳曲线

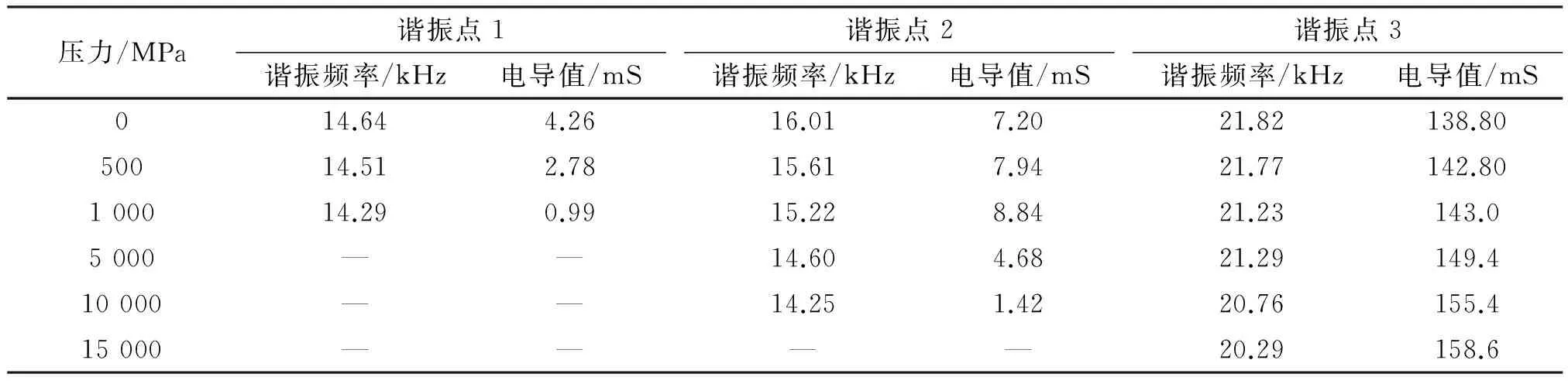
压力/MPa谐振点1谐振频率/kHz电导值/mS谐振点2谐振频率/kHz电导值/mS谐振点3谐振频率/kHz电导值/mS014.644.2616.017.2021.82138.8050014.512.7815.617.9421.77142.80100014.290.9915.228.8421.23143.05000——14.604.6821.29149.410000——14.251.4220.76155.415000————20.29158.6

提取在声轴上0.5 m处的节点的自由度解压强,经过计算得到换能器水中不同状态下的发射电压响应级曲线(见图7)。图7中,换能器的发射电压响应级曲线近似有2个峰值,随着压力增加, 低频处的峰值先略有上升后大幅下降,峰值所在频率降低,且峰的宽度变窄;高频处的峰值升高,峰值所在频率降低, 且峰的宽度变宽。表4列出了不同压表4列出了不同压力下换能器在低频段和高频段内的发射电压响应级峰值,可以看出,随着压力的增加,换能器在低频段处的发射性能先略有上升后降低,在高频段处的发射性能增强。

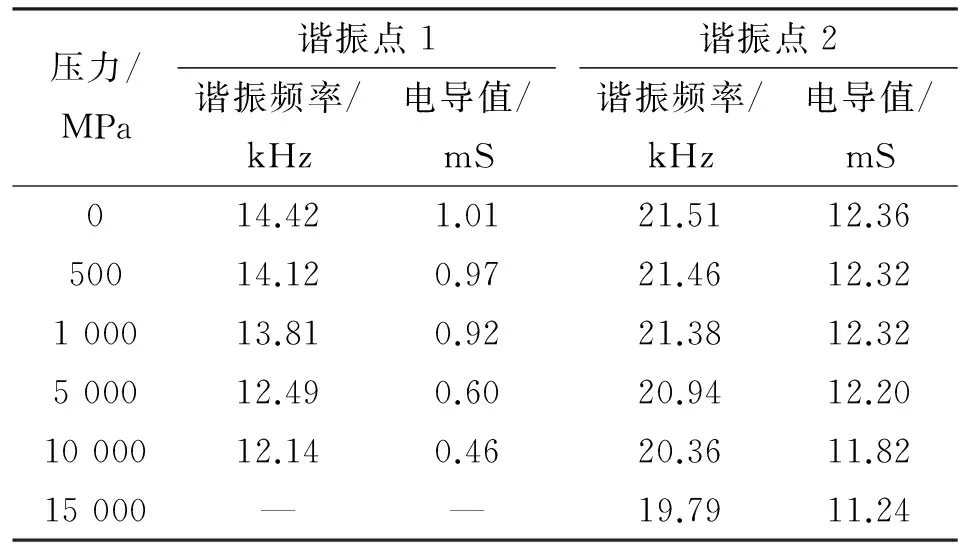
表3 水中不同压力下各个谐振点谐振频率及电导值

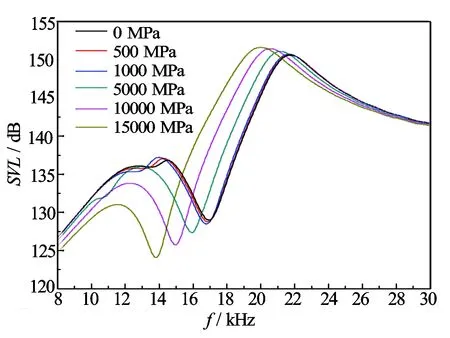
图7 换能器发射电压响应级曲线

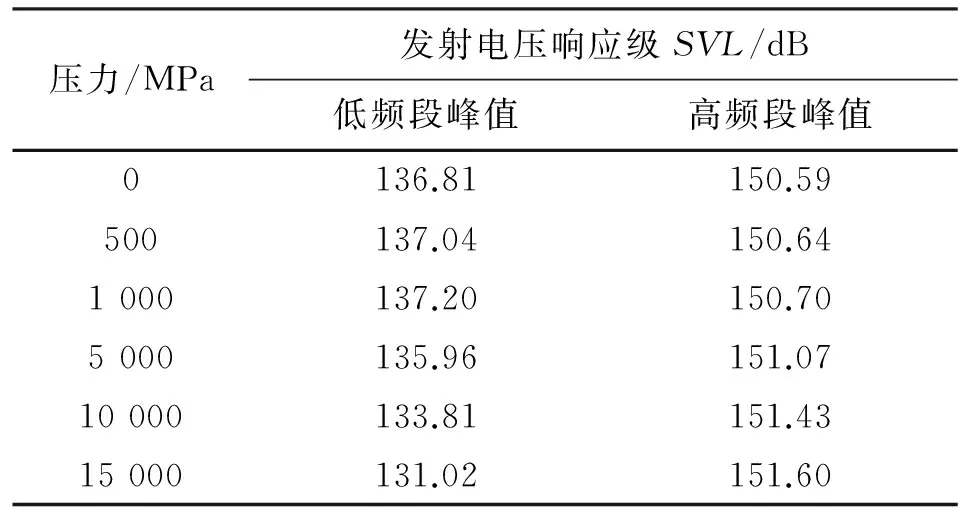
压力/MPa发射电压响应级SVL/dB低频段峰值高频段峰值0136.81150.59500137.04150.641000137.20150.705000135.96151.0710000133.81151.4315000131.02151.60

2 讨 论

由上述数值计算结果可知,随着两端压力的增加,换能器在低频段处的发射性能先略有上升后降低,在高频段处的发射性能增强。目前在裸眼井中测井的声波测井仪器,如补偿声波测井仪器、多极子阵列声波测井仪器等,所需单极子产生的声波频率在低频段,因此根据数值模拟结果,1 000 MPa的压力较适用于裸眼井声波测井仪器。在套管井中使用的声波测井仪器,如声波变密度测井仪器等,所需单极子产生的声波主频在20 kHz左右,根据图7中不同压力下的发射电压响应级曲线,15 000 MPa的压力较适用于套管井声波测井仪器。因此需根据不同声波测井仪器的需求选择不同的压力,能达到较好的效果。

3 结 论

(1) 利用有限元分析软件ANSYS对声波测井径向极化圆管换能器进行了数值模拟,计算了在不同压力载荷条件下换能器的振动模态、频率响应以及不同压力载荷对流体中换能器发射性能的影响。

(2) 随着两端压力的增加,圆管换能器的振动模态会发生变化,谐振频率降低,且当压力增大到一定数值时,某些振动模态会消失,并产生新的振动模态。

(3) 随着两端压力的增加,在空气中换能器谐振频率下降,在空气中换能器谐振频率逐渐降低,在21.82 kHz谐振点处的电导值上升,在16.01 kHz谐振点的电导值先升高后降低并逐渐消失,在14.64 kHz谐振点处的电导值降低并逐渐消失。在流体中换能器谐振频率降低,对应的电导值下降。换能器的发射性能在低频段内先略有上升后大幅下降,在高频段内上升。

(4) 不同声波测井仪器所需声波频率不同,且压电陶瓷的材料性质易碎,随着压力升高两端夹具对换能器的阻尼增大;换能器装配过程中要根据不同仪器综合各种因素选择适当的压力。

参考文献:

[1] 乔文孝, 鞠晓东, 车小花, 等. 从换能器技术的变化看声波测井技术的发展 [J]. 物理, 2011, 40(2): 99-106.

[2] 乔文孝, 鞠晓东, 车小花, 等. 声波测井技术研究发展 [J]. 测井技术, 2011, 35(1): 14-19.

[3] 楚泽涵, 高杰, 黄隆基, 等. 地球物理测井方法与原理: 上册 [M]. 北京: 石油工业出版社, 2007.

[4] 栾桂东, 张金铎, 王仁乾. 压电换能器与换能器阵 [M]. 修订版. 北京: 北京大学出版社, 2005.

[5] 莫喜平. ANSYS软件在模拟分析声学换能器中的应用 [J]. 声学技术, 2007, 26(6): 1279-1290.

[6] 吴金平, 乔文孝, 车小花. 声波测井压电振子的有限元分析 [J]. 应用声学, 2012, 31(2): 86-92.

[7] Qiao W X, Che X H, Zhang F. Effects of Boundary Conditions on Vibration Mode of Acoustic Logging Dipole Transducer [J]. Science in China, Series D: Earth Sciences, 2008, 51(Supp. II): 195-200.

[8] 王荣津. 水声材料手册 [M]. 北京: 科学出版社, 1983.

[9] 郑林, 林伟军, 王东. 三叠片型偶极声波测井换能器的有限元设计 [J]. 测井技术, 2009, 33(2): 106-109.

[10] 林书玉. 超声换能器的原理及设计 [M]. 北京: 科学出版社, 2004.