粒子群算法在砂砾岩体岩性识别中的应用

陈钢花, 王军, 程探探, 隋淑玲, 黄丽娜

(1.中国石油大学(华东), 山东 青岛 266580; 2.中国石油化工股份有限公司胜利油田分公司地质科学研究院, 山东 东营 257015; 3.山东科瑞石油工程技术研究院, 山东 东营 257067)

0 引 言

砂砾岩体在沉积过程中受水流能量和物源供给的影响,使得沉积旋回变化频繁,岩性变化快,具有非常强的非均质性和各向异性,造成砂砾岩体地质特征和测井响应之间的关系不再是单纯的线性关系,导致测井储层评价困难;砂砾岩体岩性对储层物性、含油性影响较大,准确划分岩性对计算储层参数、评价储层含油性都具有非常重要的意义。利用传统的统计方法可以划分出储层与非储层,对于复杂砂砾岩体则很难精确划分[1]。

支持向量机的基本思想是通过使用非线性映射将低维输入空间的样本映射到高维属性空间使其变为线性情况,使得在高维属性空间采用线性算法对样本的非线性进行分析成为可能[2-3]。其中核函数的选取和参数优化对回归模型的精度起到决定性的作用。粒子群算法PSO(Particle Swarm Optimization)和遗传算法相似,是从随机解出发,通过迭代寻找最优解。这种算法相比于遗传算法具有实现容易、精度高、收敛快的优点。本文针对砂砾岩地层岩性变化大、非均质性强、常规测井曲线的影响因素多、砂砾岩地层地质特征与测井曲线呈现非线性关系等特点,采用支持向量机方法对地层岩性进行划分。选用粒子群算法对支持向量机(SVM)参数进行优化,得到岩性识别模型;根据模型对研究区的30多口井的岩性进行划分,取得良好的地质应用效果。

1 粒子群算法优化SVM参数

在SVM的实际应用中涉及到参数选取问题。这些参数对分类器的分类效果具有很大的影响,直接关系到分类器分类效果。通常,需要优选的2个参数是核函数参数γ和惩罚因子C。

参数优选的原则是寻求一组最优参数,使训练得到的支持向量机对测试样本的分类预测准确率最高。本文采用k折交叉验证方法获得较为稳定的预测正确率。具体实现过程是将训练数据分成k个子集(一般是均分),先用其中(k-1)个子集作为训练样本得到一个SVM,用剩下的子集作为测试集,测试该分类器的分类准确率。如此循环进行k次,直到所有子集都作为测试样本被预测一遍,最终取该k次预测所得准确率的平均值作为最终的准确率值。实际操作时,k一般取5～10。本文采用粒子群算法对参数γ和C进行优选。

PSO算法[4]是根据鸟群觅食的规律演化出来的一种算法。PSO算法中的每一个粒子都是这个空间中的一个解。根据自己和同伴觅食的经验选择不同的飞行方向。所有的粒子都有一个被优化的函数决定的适应值,每个粒子都有一个速度决定该粒子的飞行距离和方向。然后粒子们就追寻当前的最优粒子在空间内寻找最优位置,每个粒子在飞行过程中所经历过的最好位置,就是粒子本身找到的最优解:整个种群所经历过的最优位置,就是整个种群到目前为止找到的最优解。单个粒子的最优位置被称为个体极值,整个种群的最优位置叫作全局极值。每个粒子都通过上述的2个极值不断更新自己的位置和速度,从而产生新一代群体。

利用PSO算法约束优化问题其关键在于如何处理好约束,即解的可行性。基于PSO算法的约束优化工作主要分为2类:①惩罚函数,旨在解放优化问题的约束限制;②将粒子群的搜索范围都限制在条件约束簇内,即在可行解范围内寻优。

据文献介绍,Parsopoulos等[5]运用粒子群算法与遗传算法同时求解同一问题,仿真结果显示PSO算法相对遗传算法更具有优越性;Hu等[6]采用可行解保留政策处理约束,即一方面更新存储中所有粒子时仅保留可行解,另一方面在初始化阶段所有粒子均从可行解空间取值;Ray等[7]提出了具有多层信息共享策略的粒子群原理处理约束,根据约束矩阵采用多层Pareto排序机制产生优良粒子,进而用一些优良的粒子决定其余个体的搜索方向。

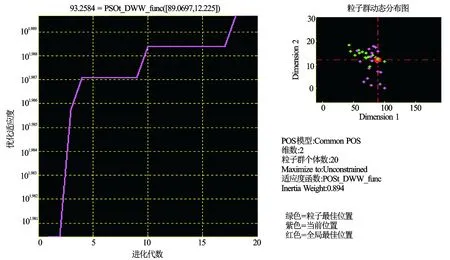
图1 粒子群算法适应度曲线图

应用粒子群算法进行SVC参数预测时先设置核函数γ和惩罚因子C的初始值,一般取值范围是0～1 000,种群大小值是20,最大的进化代数是50。利用这种方法得到的最优的核函数和惩罚因子参数值为γ=13.5987、C=45.3724,对应的验证准确率为98.943%,测试数据的准确率为83.562%。粒子群算法适应度变化的趋势见图1。 通过对比粒子群算法和遗传算法,两者的准确度都较高,回判准确率达到95%以上,测试准确率也非常高。从算法的运行过程中发现,粒子群算法的运行时间要比遗传算法的运行时间短,所以最终选择粒子群优化算法对SVM参数进行优选。

2 粒子群算法在砂砾岩体岩性识别中的应用

2.1 训练样本的选取

采用支持向量机进行砂砾岩体岩性识别,其关键是把测井信息与砂砾岩体岩性之间的非线性关系映射到多维空间的线性问题进行求解,所以首先要给定训练样本集对测井信息进行学习,以便得到解释模型。训练样本集选取的好坏直接影响到训练结果和预测模型的准确程度。训练样本选取应注意:①选出研究区各种岩性及相同岩性不同测井响应的样本;②剔除个别异常样本点;③适当控制样本点个数;④要对所选的样本集进行归一化处理,消除测井参数量纲不一致对训练结果造成的影响。

2.2 实例分析

选取反映砂砾岩体岩性的自然电位(SP)、自然伽马(GR)、声波时差(AC)、补偿中子(CNL)、地层密度(DEN)、电阻率(Rt)等6种测井参数作为输入参数,砂砾岩地层的岩性编码作为输出参数。对砂砾岩地层岩性进行预测。共选取了729个样本,其中656个样本用于训练建模,73个样本用于测试。

为了对比粒子群算法优化支持向量机参数对岩性判别的准确性,本文同时采用了遗传算法对支持向量机参数进行优选。对比结果如表1所示。从表1中数据可以看出粒子群算法的优化精度高于遗传算法,程序运行粒子群算法需要自己手动调节的参数要少于遗传算法,同时,粒子群算法达到同样的精度所需时间明显缩短。采用该种方法对支持向量机参数进行优选对砂砾岩地层的岩性进行预测具有很好的可行性。

将研究区块砂砾岩储层的岩性统计归类为15种,对656个训练样本进行回判,其中有645个样本验判正确,回判准确率为98.323%。取73个样本作为测试样本,正确的样本个数为61个, 测试准确率为83.562%,取得了理想的应用结果。利用该算法对研究区30多口井进行了处理,取得良好的地质应用效果。图2为研究区某井的岩性划分效果图。

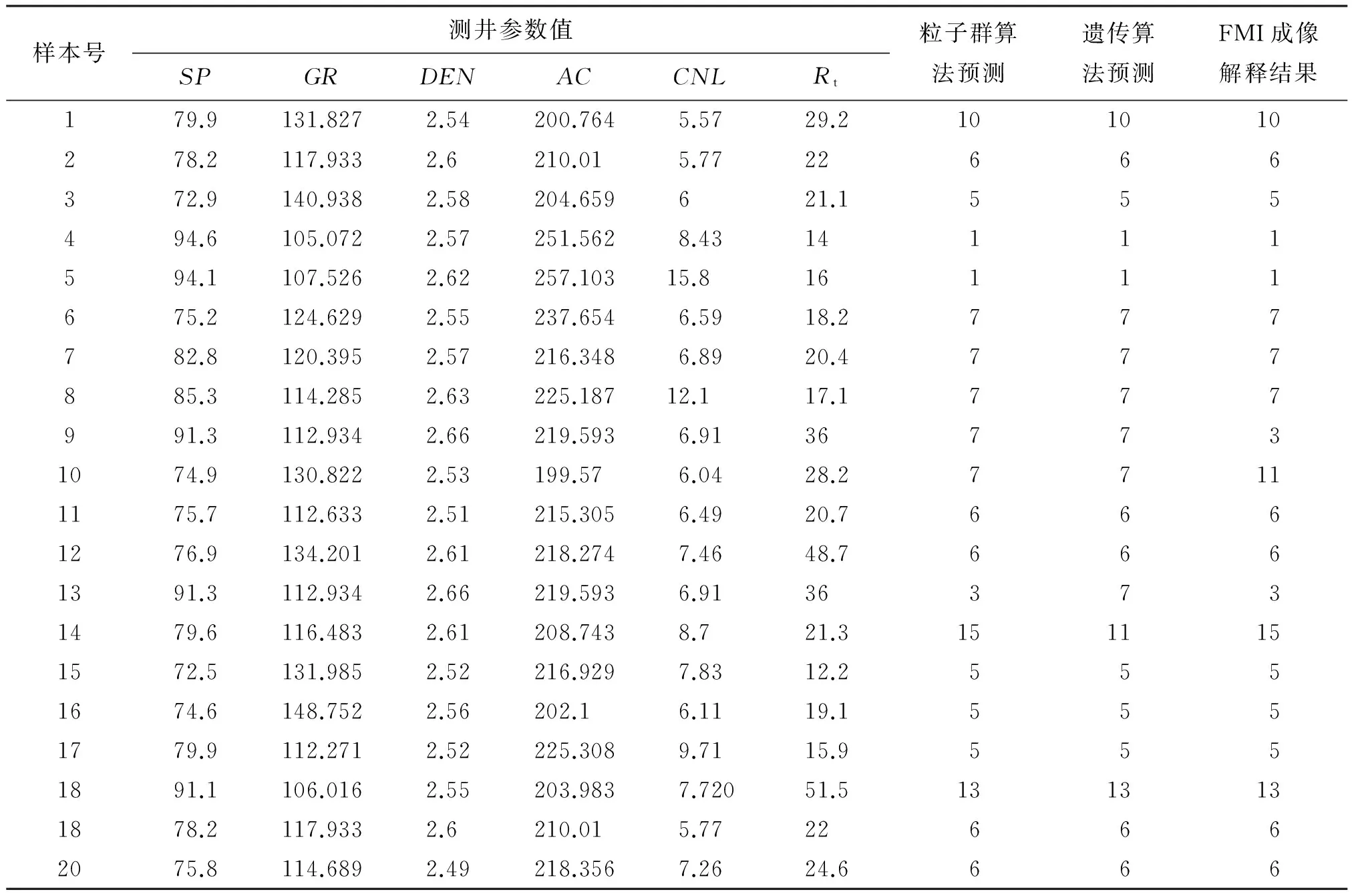
表1 粒子群算法与遗传算法结果比较表

注:1—泥岩;2—砂质泥岩;3—含砾泥岩;4—泥质砂岩;5—砂岩;6—含砾砂岩;7—砾状砂岩;8—含泥中砾岩;9—含砂细砾岩;10—含砂中砾岩;11—含砂粗砾岩;12含砂砾岩;13—细砾岩;14—中砾岩;15—粗砾岩。

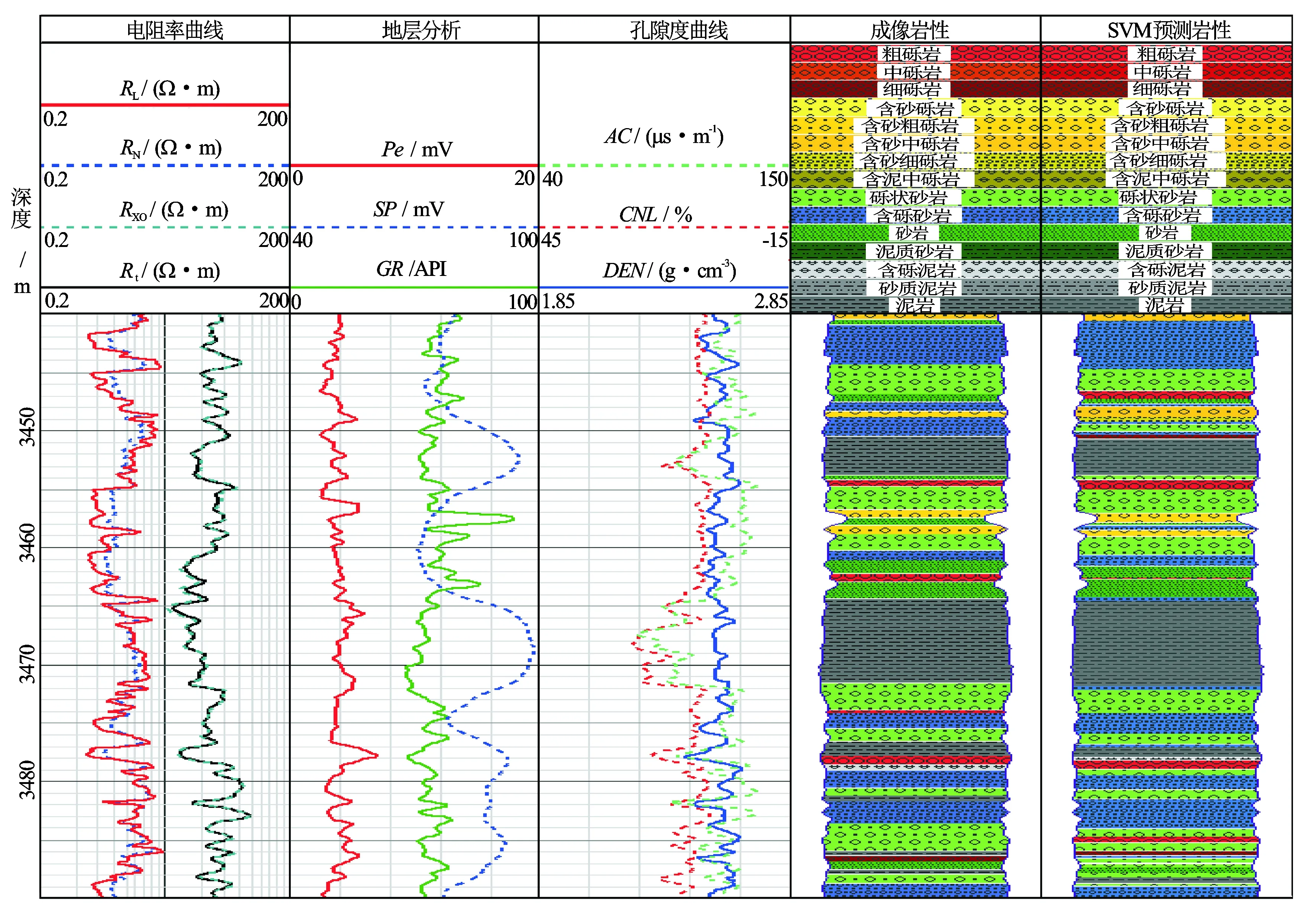
图2 基于粒子群优化算法对砂砾岩地层岩性划分示意图

3 结 论

(1) 针对砂砾岩体岩性复杂多变、非均质性强、地层地质特征与测井响应之间不再是单纯的线性关系的特点,从寻找常规测井曲线和砂砾岩体岩性的相关性出发,建立常规测井曲线和砂砾岩体岩性的统一关系,最终达到利用常规测井曲线识别岩性的目的。

(2) 对于砂砾岩体岩性与测井响应之间的非线性关系,采用支持向量机,把非线性的问题转化到高维的线性问题,从而求得测井响应与岩性的最优对应关系。

(3) 根据粒子群算法的精度高、收敛快、容易实现等优点,采用粒子群算法对支持向量机的参数进行优选,能够精确划分砂砾岩体的岩性。

参考文献:

[1] 陈钢花, 王有涛, 董维武, 等. 深层砂砾岩储层测井精细评价 [J]. 海洋石油, 2010(2): 82-86.

[2] 赵宇, 王志良, 刘冀伟. 一种基于支持向量机的测井岩性预测新方法 [J]. 微计算机信息, 2004, 20(6).

[3] 李新虎, 基于不同测井曲线参数集的支持向量机岩性识别对比 [J]. 煤田地质与勘探, 2007(3): 72-76.

[4] 杨维, 李歧强. 粒子群优化算法综述 [J]. 中国工程科学, 2004, 6(5).

[5] Parsopoulos K E, Vrahatis M. N. Particle Swarm Optimization Method in Multiobjective Problems [C]∥Proceedings of the 2002 ACM Symposium on Applied Computing (SAC 202) 2002: 603-607.

[6] Hu X, Eberhart R C. Multiobjective Optimization Using Dynamic Neighborhood Particle Swarm Optimization [C]∥Proceedings of the IEEE World Congress on Computational Intelligence, Hawaii, USA, 2002: 1666-1670

[7] Ray T, Liew K M. A Swarm Metaphor for Multiobjective Design Optimization [J]. Eng Opt, 2002, 34(2): 141-153.