动车组网侧变流器改进型dq解耦控制方法研究

阮白水, 张 钢, 蒋李晨昕, 刘志刚

北京交通大学 电气工程学院, 北京 100044)

电力牵引系统由受电弓、变压器、网侧变流器、牵引变流器和电机构成，具有高效、环保、节能以及利于维护的特点，目前已成为轨道交通的主流牵引方式。对于网侧变流器，从最早出现的二极管不控整流，到晶闸管控制的相控整流等，都会对牵引网注入大量谐波，而且无法保证网侧单位功率因数。

随着电力电子技术和功率器件制造技术的发展，采用脉宽调制技术的网侧变流器得以应用于电力牵引系统中，其具有谐波小、功率因数可控、直流电压稳定、能量双向流动的特点，目前已成为网侧变流器的首选。

网侧变流器最重要的一个环节是对网侧电流的控制，从网侧变流器的出现开始，对其网侧电流的控制一直是国内外学者研究的重点。到目前为止脉冲整流器的控制方法主要有：间接电流控制[1]、瞬态电流控制[2]、预测电流控制[3]、滞环电流控制[4]、dq旋转坐标系电流解耦控制[5，6]等方法，这些方法中除了间接电流控制外，其他的控制方法均采用双闭环的控制原理。目前在电力牵引系统中，网侧变流器的控制策略主要采用的是瞬态电流控制[7](在一些大功率开关频率很低的情况下，间接电流控制也得到了应用)，但是该控制方法难以满足列车运行过程中带来的网压波动的要求。文献[8]介绍了网压波动下网侧变流器的可变相位角控制,其本质为一种网侧无功电流注入的控制策略,若无功电流给定值为0,其可等效为瞬态电流控制。

与瞬态电流控制相比，dq解耦控制方法可以实现网侧电流有功和无功分量的分别控制，且控制对象都为直流量，从而可以实现网侧电流无静差控制[9-11]。如果根据牵引网电压波动情况来调节无功电流的给定值(例如网压低于额定时增大容性无功输出，等效于容性负载，减小网压波动加剧)，则可实现网压波动下网侧变流器的有效控制。但是传统的dq解耦控制由于引入了电流的延时分量，给系统的动态过程带来了延时和波动，这对列车这种动态性能频繁变化的系统显然是不利的[12]。

针对上述情况，本文首先介绍了传统dq解耦控制的工作原理，分析了其由于构建虚拟坐标系对动态性能带来的影响，并提出两种改进的旋转坐标系下的解耦控制方法。第一种为旋转坐标系下的瞬时电流控制，根据电压环输出的有功指令值和无功指令值，并结合旋转坐标系下的数学模型，推导出交流电压的的前馈分量，再通过比例控制器补偿前馈误差。第二种为短延时的dq解耦控制方法，即在传统dq解耦控制方法的基础上增加一个虚拟电流快速计算单元，用该单元替换原来的延时单元来获取虚拟电流，从而加快其动态性能。文章的最后通过实验波形验证了两种控制方式的有效性。

1 传统的dq解耦控制

网侧变流器结构如图1所示，其主要由牵引变压器、单相H桥、直流支撑电容和二次谐振支路组成。E为网侧电压，IS为网侧电流，Uab为单相H桥生成的电压，L为交流侧等效电感，通常集成在牵引变压器的二次侧绕组漏感中，R为等效电阻。Lr和Cr为二次谐振支路的组成部分，用于消除二次功率脉动。

图1 网侧变流器结构图

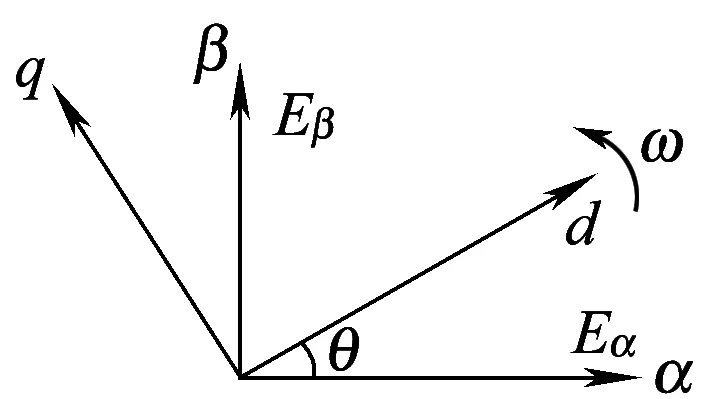
图2 旋转坐标系

文献[5,6，13]给出了传统的dq解耦控制的实现方法，其构建旋转坐标系的方法如图2所示，通过延时1/4个周期来构建与α轴正交的虚拟的β轴，从而构成两相静止坐标系，旋转坐标系与α轴的夹角为θ。如果让网压E与α轴重合，并且定义网压起始相位为0°，则有E=Eα=Emsinωt，其中Em为网压幅值。如果定义d轴为有功轴，则可求得θ=ωt-90°。进而可得

( 1 )

( 2 )

( 3 )

由于β轴为虚拟的，应用中只选取α轴的分量。

( 4 )

网侧变流器的交流侧数学模型可以表示为

Uab=E-jωLIS-RIS

( 5 )

转换到旋转坐标系下有

( 6 )

由于电阻R一般很小，往往忽略不计，借鉴三相系统前馈解耦的内环控制策略，可得

( 7 )

图3和图4分别给出了dq解耦控制的控制框图及其电流内环控制框图。从图中可以看到，因为引入了虚拟坐标系和解耦控制，可以实现有功和无功电流的分别控制，且控制对象均为直流量，从而使用PI控制器也能实现无静差控制。

图3 传统dq解耦控制的控制框

图4 电流内环控制框图

该控制方法的缺点也很明显，即在获取Ed、Eq以及Id、Iq时引入了虚拟的Eβ和Iβ，由于Eβ和Iβ是分别由Eα和Iα延时1/4个周期得到的，因此有必要分析这种延时方法对系统控制带来的影响。

将式( 1 )和式( 7 )代入式( 3 )可得

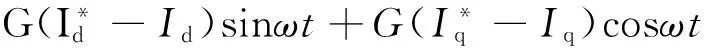
( 8 )

( 9 )

将式( 2 )代入式( 8 )可得

(10)

由于Iβ由Iα延时90°获得，有

Iβ=-jIα

(11)

则式(10)可改写为

(12)

对比式(12)和式( 5 )可以发现，dq解耦控制结果是与网侧变流器数学模型相吻合的，式(12)中等式右边最后两项分别为对有功和无功电流的闭环控制补偿量，正是这两项的存在使得有功和无功电流实现无静差控制。从推导过程中可以发现，Eβ的引入对控制结果是没有影响的，但是式(11)只在稳态下成立，在动态过程中，即电流变化的时候，实时测得的Iα做90°的移相后在幅值上不等效于1/4周期前测得的电流。由此可见传统的dq解耦控制，在电流内环的控制中势必会引入1/4周期的延时，对网侧变流器的动态过程造成延时和波动，但是对其静态性能不会造成影响。

2 旋转坐标系下的瞬时电流控制

(13)

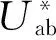
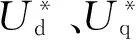
(14)

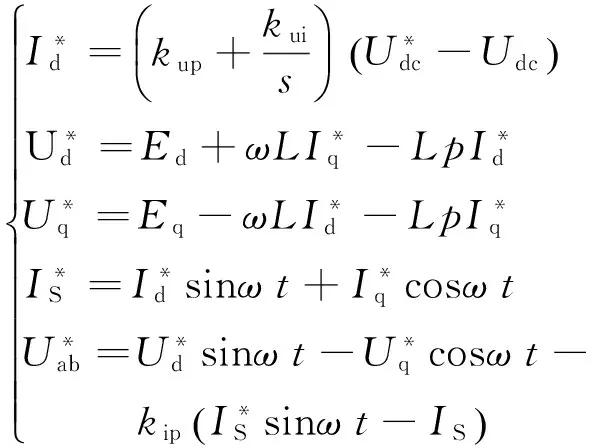
(15)

图5 旋转坐标系下的瞬时电流控制框图

相比传统的dq解耦控制而言，旋转坐标系下的瞬时电流控制由于没有引入Id、Iq的实时值，从而避免了延时分量的引入，在保证电流环快速动态性能的前提下，实现了有功和无功的分别控制。但是也正是因为没有Id、Iq的实时值，该控制方法具有以下缺陷：

(1)参与解耦控制的是有功和无功电流的指令值而不是实时值，由于两着存在误差，所以该控制方法无法实现严格意义上的解耦。

(2)电流内环不是对有功和无功电流分别进行闭环，而是对网侧电流进行闭环，由于网侧电流为交流量，因此无法实现传统dq解耦控制中的零静差效果。

可见，该控制方法虽然摒弃了dq解耦控制中最大的缺点，却也使其优点变的不那么明显，属于一种相对折中的控制方法。

3 短延时的dq解耦控制

对于传统的dq解耦控制，如果可以快速获得Iβ的值，则可以在保证其控制上固有优势的同时，使其具有更快的动态性能。对此，本文提出了一种短延时的dq解耦控制方法，即增加一个虚拟电流Iβ的快速计算单元，该单元通过网侧变流器在αβ坐标系下的表达式可以快速求出Iβ的值。

将式( 5 )转换到αβ坐标系下可得

(16)

忽略式(16)中电阻的影响，可得Iβ的表达式为

(17)

从式(17)可以看出，Iβ的值是与Eβ和Uβ相关的，在传统的dq解耦控制方法中只应用了α轴的分量，并没有利用Uβ。由于牵引网网压随着列车位移的波动是相对缓慢的，可以认为在1/4个周期内网压的幅值是不变的，即忽略1/4周期Eβ幅值的变化。由图3可以看到，要获得Uβ需要先得到Iβ的值，这与控制上的需求是相违背的。为了得到Iβ，短延时的dq解耦控制方法中利用上一个计算周期算得的Eβ和Uβ来近似求解Iβ，其控制框图如图6、图7所示，其中Z-1为单周期保持单元。

图6 虚拟电流计算单元

图7 短延时的dq解耦控制框图

短延时的dq解耦控制方法中利用上一个计算周期计算得到的Eβ和Uβ计算出Iβ，其延时仅为一个计算周期(时间长短与开关频率相关)，与传统的dq解耦控制相比，其动态性能得到了大幅度提高，而两者的静态性能是一致的。

4 实验研究

4.1 实验平台介绍

该研究的实验是基于混合动力车动车组网侧变流器的实验平台完成的，其参数见表1。混合动力车的动车组具有跨电气化铁路和非电气化铁路运行的能力，在电气化铁路中的电力牵引方式与传统的动车组相同。由于设备还处于库内静调阶段，通过对拖的试验模式(即两个网侧变流器直流侧并联，一台作为被测设备，另一台作为负载。)来验证提出的两种改进型的解耦控制方法。

表1 网侧变流器参数

4.2 传统dq解耦控制与短延时dq解耦控制对比

图8～图10所示为网侧变流器从空载升至半载(50%负载突变)的试验波形图。由于图9和图10中Id、Iq、Iα、Iβ为控制系统内部离散变量，通过D/A芯片输出，因此波形显得有一些阶梯状。从图10可以看到，传统的dq解耦控制中，Iβ是跟随Iα延时变化的，而短延时的dq解耦控制中，Iβ则是根据负载快速变化的，只有很小的延时。从图8和图9可以看到，负载变化时，传统dq解耦控制中Iβ的延时会给Id、Iq的计算结果带来延时和波动，从而影响网侧电流控制的动态性能。短延时的dq解耦控制中由于引入了Iβ的快速计算单元，其动态过程更加快速和平稳。

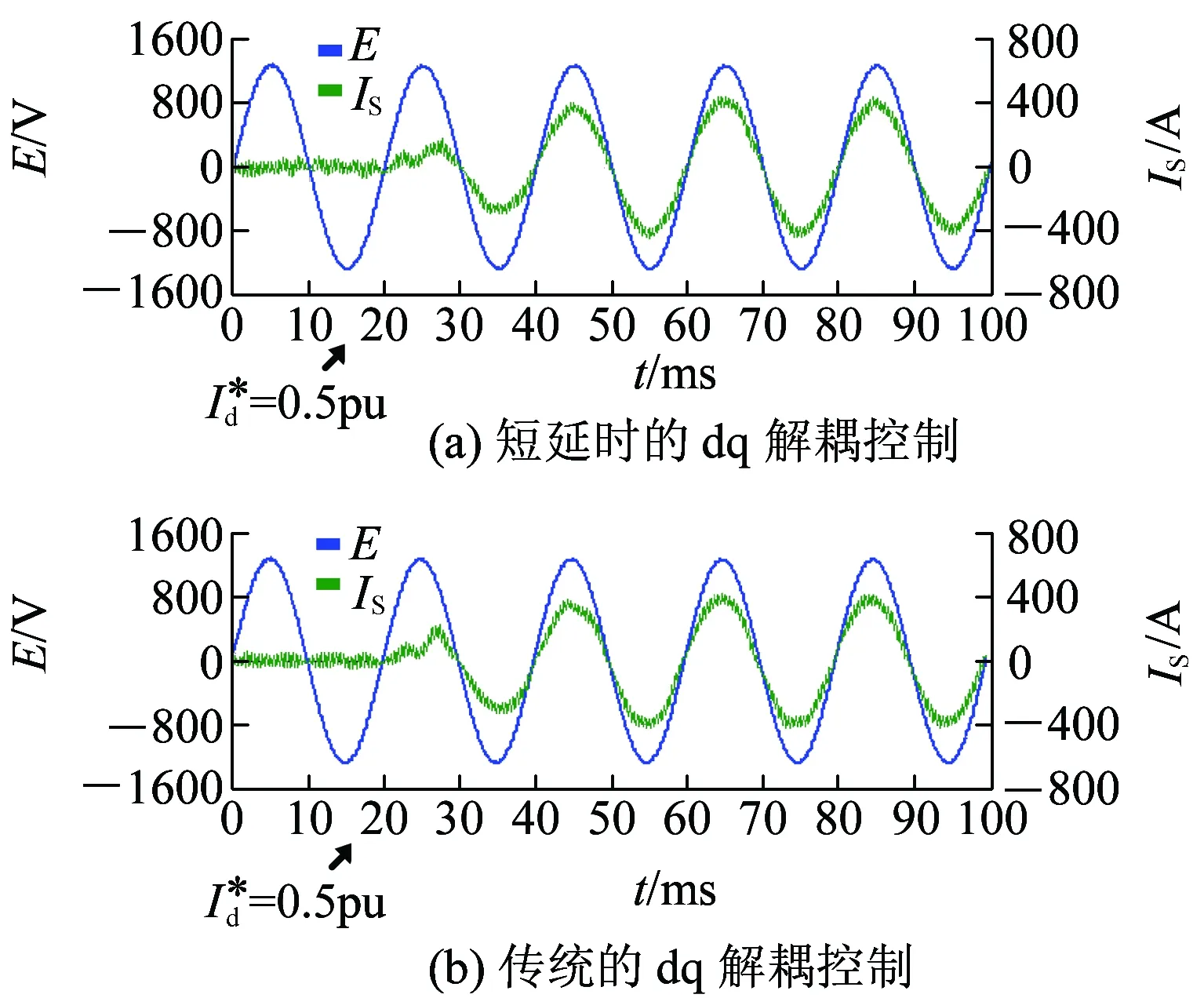
图8 空载升至半载时网压E和网侧电流IS波形

图9 空载升至半载时Id、Iq波形

图10 空载升至半载时Iα、Iβ波形

图11～图13所示为网侧变流器在半载工况下发出0.3pu容性无功的试验波形，同样可以发现短延时的dq解耦控制有更好的动态性能。

图11 发出容性无功时网压E和网侧电流IS波形

图12 发出容性无功时Id、Iq波形

4.3 旋转坐标系下的瞬时电流控制试验

图14所示为网侧变流器从空载升至半载(50%负载突变)的试验波形图及半载发容性无功的波形，对比图8和图11可以发现，旋转坐标系下的瞬时电流控制具有同样快速的动态特性，但其静态性能稍差，从图14(a)中可以明显地看到其半载时功率因数不为1。

图13 发出容性无功时Iα、Iβ波形

从试验结果可以看到，短延时的dq解耦控制同时具备良好的动态和静态性能，为最优的控制方法。

图14 旋转坐标系下的瞬时电流控制网压E和网侧电流IS波形

5 结论

针对传统dq解耦控制方法的缺点，本文提出两种改进的旋转坐标系下的解耦控制方法：旋转坐标系下的瞬时电流控制和短延时的dq解耦控制方法。文中详细介绍这两种方法的原理和实现方法，分析了其各自的优缺点。从结果中可以看到，与传统dq解耦控制相比，旋转坐标系下的瞬时电流控制具有更好的动态性能，但静态性能略差，而短延时的dq解耦控制方法能使网侧变流器同时获得良好的动态和静态性能，是最优的选择。

参考文献：

[1]KUKRER O, KOMURCUGIL H. Control Strategy for Single-phase PWM Rectifiers[J]. Electronics Letters, 1997, 33(21): 1745-1746.

[2]CHEOK A, KAWAMOTO S, MATSUMOTO T, et al. High Power AC/DC Converter and DC/AC Inverter for High Speed Train Applications[C]//Proceeding of TECON, 2000, (1): 423-428.

[3]WU R, DEWAN S, SLEMON G. A PWM AC-to-DC Converter with Fixed Switching Frequency[J]. IEEE Transactions on Industry Applications, 1990, 26(5): 880-885.

[4]LIN B, LEE Y, YANG T. AC Power Line Conditioner with Switch-clamped Topology[J].Electronics Letters, 2003,39(5): 462-464.

[5]SALAET J, ALEPUZ S, GILABERT A. Comparison between Two Methods of DQ Transformation for Single Phase Converters Control. Application to a 3-Level Boost Rectifier[C]//IEEE Power Electronics Specialists Conference, 2004: 214-220.

[6]MIRANDA U, AREDES M, ROLIM L, A DQ Synchronous Reference Frame Control for Single-Phase Converters[C]//IEEE Power Electronics Specialists Conference, Brazil: IEEE Press, 2005:1377-1381．

[7]宋文胜.电力牵引变流器控制与调制算法研究[D].成都：西南交通大学，2012.

[8]冯晓云, 电力牵引交流传动及其控制系统[M]. 北京:高等教育出版社,2009.

[9]宋文胜, 冯晓云, 谢望玉.单相三电平整流器d-q坐标系下的控制与SVPWM方法[J]. 电机与控制学报, 2012.

SONG Wen-sheng, FENG Xiao-yun, XIE Wang-yu.Space Vector Pulse Width Modulation and Control Technique for Single Phase Three Level Rectifier in d-q Coordinate System[J]. Electric Machines and Control, 2012.

[10]范声芳, 熊健, 张凯, 等. 大功率机车牵引四象限变流器解耦控制方案[J], 中国电机工程学报, 2012, 32(21):63-70.

FAN Sheng-fang, XIONG Jian, ZHANG Kai, et al.A Decoupling Control Scheme of High Power Four-quadrant Converters for Traction[J]. Proceedings of the CSEE, 2012, 32(21):63-70.

[11]陶兴华, 李永东, 孙敏,等. 一种基于同步旋转坐标变换的单相锁相环新算法[J]. 电工技术学报, 2012,32(21):147-152.

TAO Xing-hua, LI Yong-dong, SUN Min,et al. A Novel Single-Phase Locked Loo PAlgorithm Based on Synchronous Reference Frame[J]. Transactions of China Electrotechnical Society, 2012,32(21):147-152.

[12]李伟. 基于坐标变换的单相四象限整流器控制[J]. 电气传动, 2011,41(10)：33-36.

LI Wei. Single- phase 4QC Rectifier Control Based on Coordinate Transformation [J]. Electric Drive, 2011,41(10):33-36.

[13]李红波, 张凯, 赵晖, 等. 基于功率解耦的高功率密度单相整流器[J].电工技术学报, 2011, 26(1):77-82.

LI Hong-bo, ZHANG Kai, ZHAO Hui, et al. A High Power Density Single Rectifier with Power Decoupling Function[J]. Transactions of China Electrotechnical Society, 2011,26(1):77-82.