机车车轮磨耗统计数据处理方法与镟修周期预测模型

TAO VAN CHIEN(越), 李 芾, 戚 壮, 丁军君

西南交通大学 机械工程学院，四川 成都 610031)

自19世纪80年代铁路诞生以来，轮轨磨耗一直是世界铁路行业难以解决的问题。近年来，铁路行业的专家学者及工程师采用了各种方法和措施来降低轮轨磨耗,如优化轮轨踏面匹配以减少车轮接触应力，研究轮轨新材料，改善机车车辆悬挂参数以减少轮轨之间的动力学作用等。铁路高速重载的发展趋势加剧了轮轨作用，导致车轮和钢轨间的磨耗也越来越严重。这不仅增加了铁路的运输成本,甚至会直接危害行车安全。因此，对机车车辆的轮轨磨耗进行研究，具有重要的理论意义和工程应用背景[1]。

机车车轮磨耗是一个复杂且严重的问题，由很多的复杂机理形成，主要包括轮轨摩擦学、轮轨关系、材料学和固体力学等。国内外学者开展了大量的研究工作，主要集中在轮轨滚动接触理论、磨耗与滚动接触疲劳、磨耗的实验与仿真等。Jendel等基于Hertz 理论及Archard模型预测了通勤车辆在斯德哥尔摩铁路网运行后的磨耗状态，数值结果与现场测量结果比较吻合。文献[1]采用Winker模型分析轮轨接触，并比较了Winker模型与有限元算法对磨耗预测的影响。文献[2]发展了三维弹性体非赫兹滚动接触理论和数值程序CONTACT。文献[3]介绍了非椭圆接触班内接触区域和法向接触应力的计算方法。文献[4]为了使轮轨法向接触的准确性和计算效率得到统一，提出了一种新的轮轨接触算法，并与赫兹接触和CONTACT进行比较。文献[5]利用车辆-轨道耦合动力学模型、CONTACT程序和Archard磨耗模型分析了曲线上车轮的磨耗情况。文献[6]基于半赫兹接触、赫兹接触和Kalker完全理论程序CONTACT 分别计算轮轨接触应力和接触形状，并计算车轮磨耗深度在踏面上的分布。

目前，越南铁路的机车均由国外进口，镟修周期基本由制造厂家提出，但机车在越南铁路的实际运用条件与其设计条件有很大差别，因此车轮在两次镟修之间的磨耗量也有别于其初始设计值。车轮在实际中磨耗过大，会影响行车安全，但车轮在镟修周期间磨耗不足，则会增加机车车辆和线路的检修维护工作量。因此，依靠实际运用中的车轮磨耗统计数据来决定或者调整镟修周期是一种保证行车安全且降低维护工作量的合理可行的方法。本文针对越南铁路实际运营中的磨耗统计数据对其概率分布律进行研究，并基于所建立的机车车轮磨耗统计数据处理程序得到了随机数据统计的概率密度分布曲线、概率分布曲线及其随机数据特征。将该模型应用于C0-C0机车的车轮磨耗研究，并计算了该型机车的车轮镟修周期。

1 统计数据处理方法与建模

对机车车轮磨耗数据进行处理时，首先将数据输入程序，通过统计对数据进行分组，并计算频数、频率、期望数学、均方差；计算χ2误差；按照χ2标准与分布律的自由系数对实验分布与理论分布的合适性进行检验，其计算流程如图1所示。

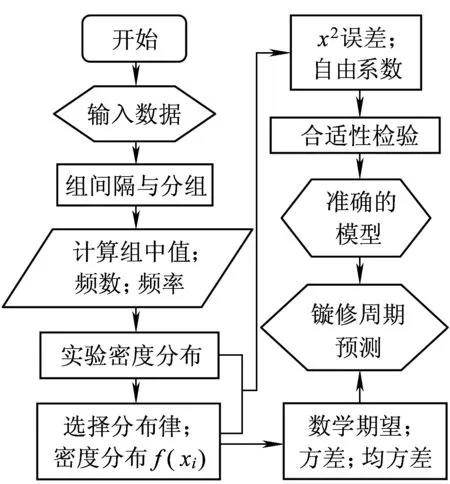
图1 车轮磨耗统计数据处理流程图

根据文献[7-9]，在计算流程中，采用式( 1 )确定分组间隔h。

( 1 )

式中：x为随机统计数据；k=1+3.32lg(n),n为统计数据的数量。

在确定了每组数据的统计特征后，需要选择特定的分布律对理论分布与实际分布的合适性进行检验。根据文献[7, 10]，本研究采用7种分布律进行建模，其中包括：正态分布、对数正态分布、指数分布、Γ分布、威布尔分布、Reyleigh分布以及Maxwell分布。以上各分布律的概率密度函数可参考数学手册，此处不再赘述。

在对磨耗统计数据选择合适的分布律时，需要对统计数据与每种分布律的吻合程度分别进行检验。根据文献[9，11,12]，统计数据与待选分布律的吻合程度采用PEARSON提出的χ2标准(Chi-square deviation)进行计算。

( 2 )

式中：f(xi)为待选分布律第i组的概率密度；pi为实验分布的概率密度。

若统计数据与待选分布律吻合，则满足χ2标准的条件概率为

P(χ2,L=k-s-1)>α

( 3 )

式中：L为自由系数；s为分布参数;k为分组量;α为检验水准，通常取α=0.05；P(χ2,L)通过查相关数值表可以得到。

该条件满足，说明待选分布律与统计数据相吻合。采用该分布律对统计数据进行建模，可满足模型的计算精度与可靠性，并可将其应用于车轮磨耗的预测。

基于Matlab 软件，编制了随机数据处理与车轮磨耗预测程序。该程序可以对输入的车轮磨耗统计数据正确地选择合适的分布律并建立车轮磨耗预测模型，按照不同的可靠度自动计算机车车轮的镟修周期。在本研究中，需要处理的随机数据为C0-C0机车车轮磨耗数据，处理过程分别对整车车轮磨耗数据、每个车轮磨耗数据、每根轴车轮磨耗数据以及机车左、右车轮的磨耗数据分别处理。

2 计算结果与模型比较分析

2.1 计算结果

越南铁路从SIEMENS 公司引进了16台D20E型内燃机车，该型机车配属岘港机务段，其标称功率为1500 kW(2 000 hp)，最高运行速度为120 km/h[13]。应用上述程序对D20E型内燃机车的车轮磨耗数据进行处理。该数据于2007～2009年期间统计，统计持续时间长，采集数据准确度高，保证了数据分析具有较高的可信度。输入数据后，程序会自动对7种分布律的合适性进行分析。结果显示，D20E型机车车轮磨耗速率数据统计符合正态分布和Γ分布，检验结果列于表 1。

表1 实验分布与理论分布合适性检验结果

基于正态分布和Γ分布的概率密度函数，可得到机车车轮磨耗速率的密度曲线拟合方程为

( 4 )

( 5 )

D20E型机车车轮磨耗速率统计数据分组密度分布与正态分布和Γ分布的概率密度函数曲线如图2所示。由图2可知，平均磨耗速率为2.329 mm/105km, 磨耗速率2.289～2.601 mm/105km所占概率最大，大部分磨耗速率分布在1.977～2.601 mm/105km之间，占50.52%。计算出的机车车轮磨耗速率特征见表2。

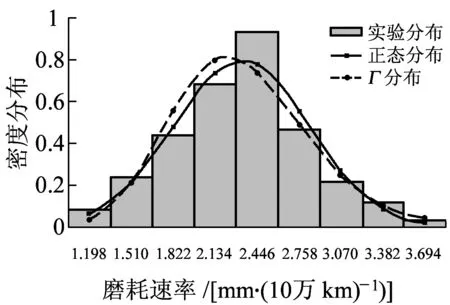
图2 D20E型机车车轮磨耗速率实验分布与理论分布密度曲线

序号分组区间组中值xi频数mi频率ri实验密度pi密度分布f(xi)概率分布F(xi)正态分布Γ分布正态分布Γ分布11.041～1.3531.19750.0260.0830.0630.0320.0120.00321.353～1.6651.509140.0720.2330.2100.2110.0510.03631.665～1.9771.821260.1350.4330.4770.5560.1560.15441.977～2.2892.133410.2130.6840.7350.7960.3490.37252.289～2.6012.445560.2920.9340.7710.7320.5920.61862.601～2.9132.757280.1450.4670.5510.4820.8030.80972.913～3.2253.069130.0670.2160.2670.2430.9290.92083.225～3.5373.38170.0360.1160.0880.0990.9820.97293.537～3.8493.69420.0100.0330.0190.0340.9960.991总计n=1921

2.2 模型比较分析

统计数据与正态分布模型和Γ分布模型的拟合相关系数分别为R=0.970、R=0.949，这说明正态分布模型的拟合效果更好。

同时，由图2可以看出磨耗速率在2.289～2.601 mm/105km所占比例最大，正态分布模拟数据显示此值为2.329 mm/105km，Γ分布模拟数据显示此值为2.143 mm/105km，偏离实际值较大。此外，由统计数据结果可知，几乎没有磨耗速率在3.694 mm/105km以上，而Γ分布曲线末端，曲线仍不接近为零，表明有部分磨耗速率大于3.694 mm/105km，与实际有所偏差。

将x取值为0～3.694，对图2中不同磨耗速率比例进行累积，绘制出累积磨耗速率分布图，即概率分布，如图3所示。

对于正态分布模型，磨耗速率在3.694mm/105km以内所占比例为

( 6 )

由此说明，磨耗速率在3.694 mm/105km以内占99.6%，磨耗速率在3.694 mm/105km以上比例很少，与统计结果吻合。

图3 D20E型机车车轮磨耗速率的概率分布曲线

对于Γ分布模型，此积分值为

( 7 )

该计算结果表明，磨耗速率在3.694 mm/105km以内占99.1%，比正态分布的要小，不能很好反映本次统计的实际情况。对车轮磨耗数据处理过程中，正态分布模型较Γ分布模型更能准确反映磨耗速率的情况。

将统计数据结合正态分布模型计算可得此模型参数结果，见表3。

表3 正态分布模型参数结果

2.3 车轮磨耗数据局部处理

为方便分析，将机车的两个转向架分别编号为I和II，将整车12个车轮沿列车走行方向从左至右编号，如图4所示[1]。奇数为左侧车轮，偶数为右侧车轮。利用正态分布模型，分别对每个车轮磨耗数据、每根轴车轮磨耗数据以及机车左、右轮的磨耗数据分别处理，结果如图5所示。

图4 机车车轮编号示意图

图5给出12个车轮的磨耗速率对比情况。局部磨耗数据处理结果显示，1位轮对磨耗速率最高，为2.802 mm/105km；6位轮对磨耗速率最小，为1.877 mm/105km，前者是后者的1.4倍。综合磨耗数据处理结果显示: 在机车每个转向架上，导向轴轮对磨耗速率明显大于其他两轴：1轴车轮的磨耗速率是3轴的1.35倍；4轴是6轴的1.37倍。此外，左轮磨耗速率比右轮磨耗速率略大，约为1.02倍。从图2、图3来看，占比例最大的机车车轮磨耗速率为2.289～2.601 mm/105km，所占比例为29%。整车车轮磨耗速率的数学期望为E(x)=2.329 mm/105km，即机车车轮的均匀磨耗速率，该参数是机车车轮运行周期预测的重要参数之一。

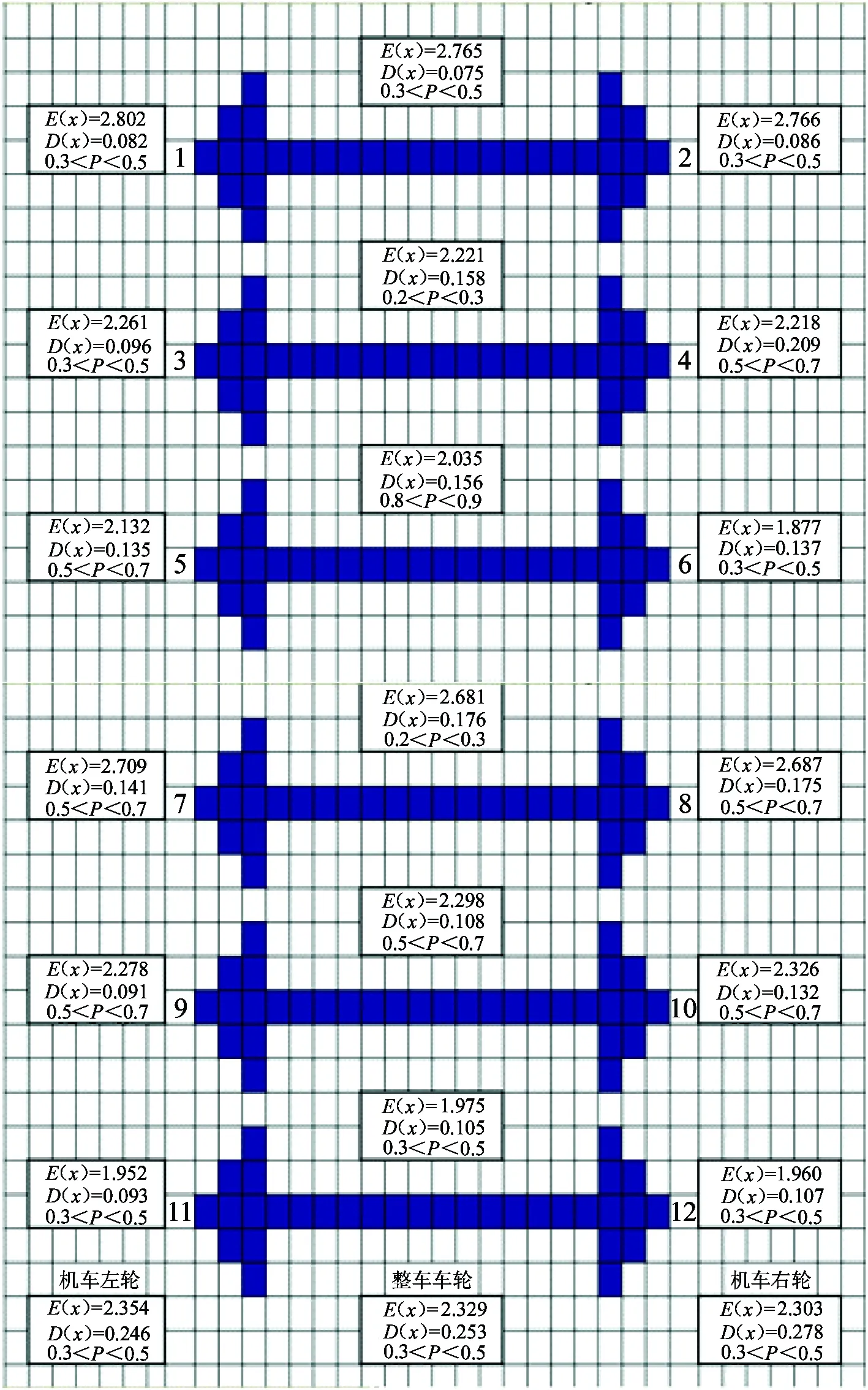
图5 D20E 型机车车轮磨耗数据统计的正态分布局部处理的结果

3 D20E机车车轮镟修周期预测

3.1 正态分布模型

以上结果表明，D20E型机车车轮磨耗速率的统计数据符合正态分布，其数学期望为E(x)，方差为D(x)。机车运行L里程后，机车车轮磨耗深度h也符合正态分布，其数学期望为E(h)=E(x)×L，方差为D(h)=D(x)×L2。

基于正态分布的概率密度函数，可以得到机车车轮磨耗深度的概率密度为

( 8 )

车轮磨耗深度未超过限值的概率可用可靠度函数P(L)来计算。

( 9 )

将式( 8 )代入式( 9 )可得

(10)

式中：Φ(z)为Laplats函数；hgh为磨耗限值， mm。

若确定了未超磨耗深度车轮的概率，可通过查表得到z值，计算出机车的运行里程。

(11)

由表3数学期望与方差的计算结果，结合越南铁路总公司规定，机车车轮磨耗深度限制值hgh=7.0mm[14]。当P(L)取不同的值时，经过计算可得到对应的机车磨耗到限运行里程，见表4。

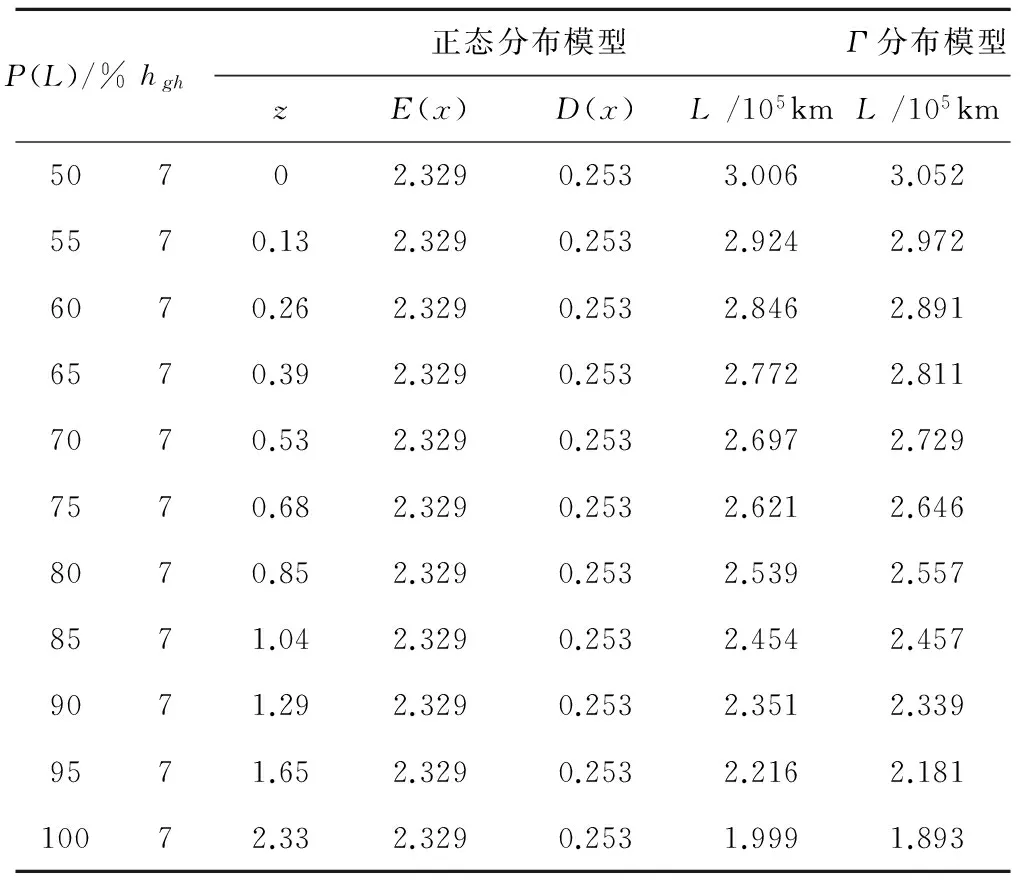
表4 D20E型内燃机车车轮运行里程

3.2 Γ分布模型

机车运行L里程后，车轮磨耗深度为h。基于Γ分布的概率密度函数，可以得到机车车轮磨耗深度的概率密度为

(12)

式中：λ(h)、η(h)为Γ分布参数；Γ(η(h))为Γ函数。

(13)

(14)

μ(x)、β2(x)分别为车轮磨耗速率的数学期望与方差。将统计数据进行计算可得μ(x)=2.329，β2(x)=0.253。

车轮磨耗深度未超过限值的概率可用可靠度函数P(L)来计算。将式(12)代入式( 9 )可得

(15)

经过计算可以得到机车磨耗到限的运行里程，见表4。由表4可知，正态分布模型和Γ分布模型的结果比较接近，最大相差率为5.4%。基于上述分析，正态分布模型较Γ分布模型更能准确反映磨耗速率的情况，所以用正态分布模型对该机车车轮镟修周期预测更准确。

由于车轮是机车的重要部件之一，对其可靠性有很高的要求，故P(L)应取90%～100%之间，其对应的镟修周期为2.2×105km左右。而越南铁路在实际中对D20E型机车的平均镟修周期为1.8×105km[14]。可根据计算结果对镟修周期进行调整，不但能够保障机车的行车安全性，还能在很大程度上降低运行成本。

4 结论

基于统计学方法，对机车车轮的磨耗数据进行处理，并按照χ2标准分别对7种概率分布的合适性进行了检验。本研究通过对D20E型机车车轮磨耗数据进行计算，绘制了D20E型机车车轮磨耗速率的密度分布与概率分布曲线并计算出了其数学期望与方差。由计算结果预测了该型机车的车轮镟修周期，主要得到以下结论：

(1)正态分布模型能准确反映D20E型机车车轮磨耗数据的实际情况，其平均磨耗速率为2.329 mm/105km,大部分磨耗速率分布在1.977～2.601 mm/105km之间，占50.52%。

(2)为了满足车轮在机车运行中的可靠性，未到限磨耗车轮的概率限制为90%～100%，可预测出D20E型机车车轮镟修周期约为2.2×105km。

(3)根据理论计算得出的车轮镟修周期结果，铁路管理部门可进一步考虑机车行车安全度与运营成本等其他重要影响因素，合理确定出符合铁路实际运营状况的机车车轮镟修周期。

参考文献：

[1]李霞，金学松，温泽峰，等. 计算铁路车轮轮周磨耗量的两种方法对比[J]. 工程力学，2011, 28(1): 205-211.

LI Xia, JIN Xue-song, WEN Ze-feng, et al. Comparison of Two Methods for the Calculation of Railway Wheel Circumference Wear[J]. Engineering mechanics, 2011, 28(1): 205-211.

[2]郭俊，李霞，杜星，等. 车轮磨耗分析中平滑方法的选取[J]. 西南交通大学学报，2010, 45(3): 373-377.

GUO Jun, LI Xia, DU Xing, et al. Selection of Data Smoothing Methods in Wheel Wear Analysis[J]. Journal of Southwest Jiaotong University, 2010, 45(3): 373-377.

[3]KIK W, PIOTROWSKI J. A Fast, Approximate Method to Calculate Normal Load at Contact between Wheel and Rail and Cree PForces During Rolling [J]. The 2ndMini Conference on Contact Mechanics and Wear of Rail/Wheel Systems. Budapest,1996: 52-61.

[4]ALONSO A, GIMENEZ J G. A New Method for the Solution of the Normal Contact Problem in the Dynamic Simulation of Railway Vehicles [J]. Vehicle System Dynamics, 2005, 43(2)：149-160.

[5]李霞，金学松，胡东. 车轮磨耗计算模型及其数值方法 [J]. 机械工程学报，2009, 45(9): 193-200.

LI Xia, JIN Xue-song, HU Dong. Theoretical Model and Numerical Method of Wheel Profile Wear[J]. Journal of Mechanical Engineering, 2009, 45(9): 193-200.

[6]丁军君, 李芾，黄运华. 基于半赫兹接触的车轮磨耗计算[J]. 西南交通大学学报，2011, 46(2):195-201.

DING Jun-jun, LI Fu, HUANG Yun-hua. Calculation of Wheel Wear based on Semi-Hertzian Contact[J]. Journal of Southwest Jiaotong University, 2011, 46(2): 195-201.

[7]Do Duc Tuan. Ly Thuyet do Tin Cay [M]. Ha Noi: Truong Dai hoc Giao thong Van tai, 2007.

[8]林洪桦. 非正态分布误差的统计处理[J]. 宇航计测技术，1996, 16(4): 6-15.

LIN Hong-hua. Statistics Processing of Error of Non-normal Distribution [J]. Aerospace Measuring Technology, 1996, 16(4): 6-15.

[9]董锡明. 机车车辆运用可靠性工程[M]. 北京: 中国铁道出版社，2004.

[10]叶其孝，沈永欢. 实用数学手册[M]. 北京: 科学出版社，2006.

[11]韩春明. 对数正态分布密度函数有关参数的计算及其成因讨论[J]. 新疆工学院学报, 1997， 18(3): 222-226.

HAN Chun-ming. Discussion on Calculation and the Causes of the Lognormal Distribution Parameters of Density Function[J]. Journal of Xinjiang Institute of Technology, 1997, 18(3): 222-226.

[12]江希钿,王笃治. 关于利用χ2检验地位指数曲线方法的研究[J]. 云南林业调查规划, 1989, (2): 35-39.

.JIANG Xi-dian, WANG Du-zhi. Study Usingχ2Test Status Exponential Curve Method[J]. Forestry Survey Planning of Yunnan, July, 1989, (2): 35-39.

[13]曹文战，安琪，李芾. 越南机车的发展现状与展望[J].国外铁道机车与动车, 2013,(4):28-33.

CAO Wen-zhan，AN Qi, LI Fu. The Development Status and Prospect of Vietnam Locomotive[J]. Foreign Railway Locomotive and Motor Car, 2013, (4):28-33.

[14]Tong Cong ty Duong Sat Viet Nam. Quy Trinh Sua Chua Dau May D20E[Z]. Ha Noi: Tong cong ty duong sat, 2008.