水下盾构隧道双层衬砌分析模型的比较研究
2015-05-09晏启祥姚超凡
晏启祥,姚超凡,何 川,耿 萍
西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031)
双层衬砌结构在补强、防火、防撞、抗沉降、防侵蚀等方面相对单层管片衬砌更具优势,因此,其在我国大型跨江越海水下隧道中运用越来越多,如杭长客运专线钱塘江隧道、广深港客运专线狮子洋隧道以及正在论证的琼州海峡跨海通道隧道方案等均设置双层衬砌。双层衬砌是指在单层管片衬砌内部模筑二次衬砌形成的一种隧道结构型式,如图1所示。
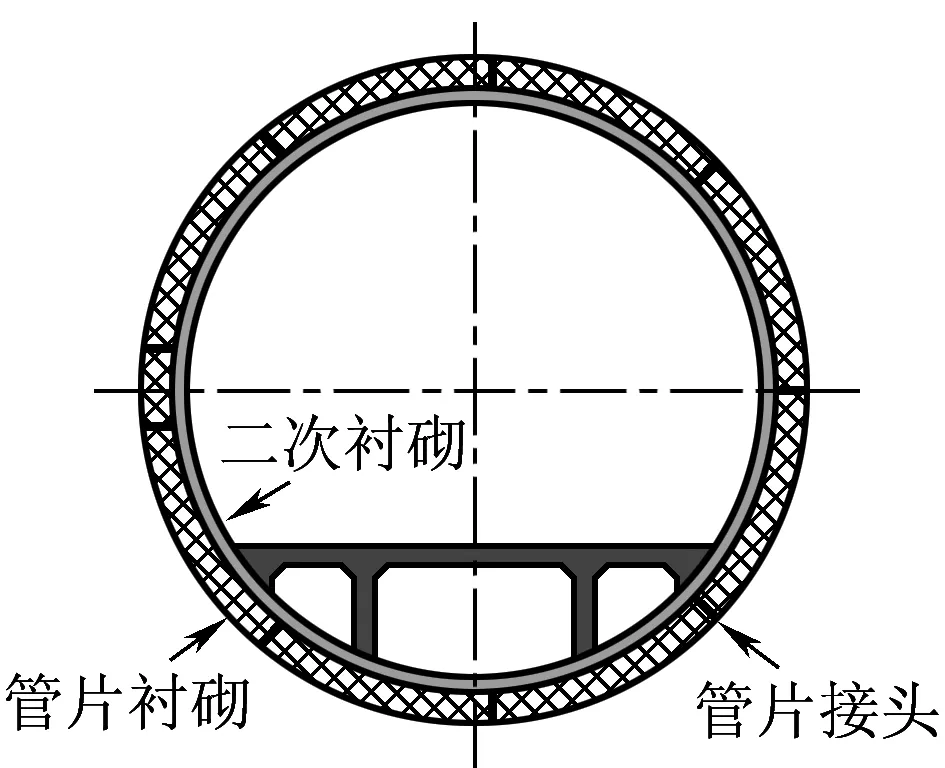
图1 双层衬砌示意
国内外对盾构隧道的研究主要集中在单层衬砌。文献[1]阐述盾构隧道设计的基本步骤,为盾构隧道设计者提供包含盾构隧道分析方法的设计指南。文献[2,3]通过管片环原型试验、理论解析等方法研究隧道横向结构力学特征,探讨了结构纵向稳定性及其减震措施。文献[4]分析衬砌管片的接头效应,研究接头数量和地层参数对管片弯矩的影响。文献[5]通过数值模拟,研究不同荷载下管片接头转角与抗弯刚度的变化规律。针对盾构隧道双层衬砌结构分析方法和力学行为的研究国内外尚不多见,文献[6,7]相对较早提出荷载结构模式的梁-弹簧模型,并在结构力学和弹性力学基础上推导模型参数的相关计算公式,但其并未系统给出数值分析模型。国内对双层衬砌的研究目前主要集中在管片接头和结合面方面[8],并根据二次衬砌施工的不同工艺将双层衬砌结合面分为3类,即纯抗压、抗弯剪压、抗剪压并局部抗弯。抗弯剪压是针对管片衬砌表面的注浆孔、螺栓孔和凹槽填充,且对管片衬砌表面进行凿毛处理后施作二次衬砌的情况。由于国内多数盾构隧道双层衬砌的二次衬砌施工工艺符合抗弯剪压原理,研究重点应放在论证抗弯剪压作用原理下的数值模型。针对当前盾构隧道双层衬砌抗弯剪压原理下的各种分析模型,从数值力学角度探讨其合理性将直接关系到双层衬砌力学特性的揭示和分析,因此开展各种数值模型对比具有重要意义。
1 双层衬砌模型
目前,基于抗弯剪压原理和荷载结构模式的国内外盾构隧道双层衬砌数值分析模型主要有衬砌梁-接头弹簧-结合面梁模型[9](以下简称模型1)、衬砌梁-接头弹簧-结合面弹簧模型(以下简称模型2)以及衬砌梁-接头弹簧-结合面压杆弹簧组合模型(以下简称模型3),如图2所示。除此之外,衬砌梁-接头弹簧-结合面接触摩擦模型也偶被提及。上述3种主要模型的共同点是管片衬砌和二次衬砌均采用梁单元模拟,管片接头采用弹簧单元模拟,管片与地层接触面切向连接采用弹簧单元模拟。设置结合面的切向弹簧时,采用点位移耦合方式将管片衬砌点和对应二次衬砌点的位移提取到切向弹簧两端以模拟结合面切向力,如图2(b)、图2(c)所示。

(a)衬砌梁-接头弹簧-结合面梁模型

(b)衬砌梁-接头弹簧-结合面弹簧模型

(c)衬砌梁-接头弹簧-结合面压杆弹簧组合梁模型图2 3种盾构隧道双层衬砌模型
由图2可见,3种模型的不同主要是结合面的处理。衬砌梁-接头弹簧-结合面梁模型用单一径向梁单元模拟管片衬砌与二次衬砌间径向力和切向力的传递;衬砌梁-接头弹簧-结合面弹簧模型采用径向弹簧和切向弹簧模拟结合面径向力和切向力的传递;衬砌梁-接头弹簧-结合面弹簧压杆组合模型用只能承压的杆单元模拟管片与二次衬砌结合面以及管片与地层接触面的径向连接,结合面和地层接触面切向力的模拟皆采用弹簧单元。
3种模型的荷载结构示意图大体相似,本文以衬砌梁-接头弹簧-结合面弹簧压杆组合模型加以说明,其荷载结构模型如图3(a)所示,采用水土合算的荷载模式,土压力采用太沙基理论进行计算。图3(a)中p、q分别为上覆土压力和基底反力,e1、e2分别为拱顶和拱底的侧向土压力。管片接头处设置拉压弹簧、剪切弹簧和抗弯弹簧来模拟各方向力的传递,拉压弹簧和剪切弹簧采用点位移耦合方式,如图3(b)所示,即图中点1和点2、点3和点4的位移分别耦合一致,实现点2和点3之间的剪切可用点1和点2之间的剪切弹簧模拟。

图3 双层衬砌荷载结构模型及其管片接头处理
鉴于3种模型在结合面和地层接触面的处理上采用不同的方式,为探明各种模型的合理性,下面将对3种模型开展对比研究以评估各种模型的合理性。
2 双层衬砌模型的对比分析
2.1 参数确定方法
2.1.1 双层衬砌结合面径向和切向刚度
当管片衬砌拼装完成后,二次衬砌直接现场浇注,双层衬砌可视为叠合式衬砌结构[6,7],如图4(a)所示。

图4 叠合式衬砌结构及其参数取值方法
假定层间压缩刚度等于内外衬砌各一半厚度压缩区内混凝土柱的压缩刚度[6,7],双层衬砌压缩刚度和切向刚度分别为
( 1 )
( 2 )
式中:Ky、Kt分别为双层衬砌结合面的径向刚度和切向刚度,kN/m;E1、E2分别为管片衬砌与二次衬砌混凝土的弹性模量,kN/m2;G1、G2分别为管片衬砌与二次衬砌混凝土的剪切模量,kN/m2;t1、t2分别为管片衬砌与二次衬砌的厚度,m;A为压缩区面积,A=B×θ×R,m2,如图4(b)所示,B为双层衬砌幅宽,θ为计算角度,R为结合面半径。
2.1.2 地层结构接触面径向及切向刚度
由于管片衬砌刚度远大于地层刚度,可以近似认为管片衬砌刚度对地层接触面刚度无影响。地层接触面径向刚度可以表示为[10]
融资租赁也可以叫作金融租赁,也就是承租方依据自身需求,对出卖方及租赁设备进行选择,接着,出租方按照承租方的需求来购置相应的出租物,再出租给承租方[1]。在这种租赁模式下,因为设备都是有承租企业提供的,所以,出租人不需要对设备的使用性能、维修管理等各方面负责。融资租赁流程如图所示。在此流程下,若是承租方租赁的设备到期,可以停租。
Kr=kr×A
( 3 )
式中:kr为地层径向抗力系数,kN/m2;A为地层与管片衬砌接触面积,m2,计算方法与图4(b)所示方法类似;地层接触面切向刚度可近似取径向刚度的一半。
2.2 分析对象与取值
以国内某水下双层衬砌盾构隧道为例进行对比分析,该隧道内径10.9 m,外径12.5 m,环宽2.0 m。管片衬砌采用“6+2+1”分块型式,采用通用楔形环拼装,钢筋混凝土管片衬砌厚0.5 m,二次衬砌厚0.3 m。由分析可知,结合面单元数量对特定模型的计算精度有较大影响,对本算例而言,当结合面单元数量大于1 500个时,计算的结果基本趋于稳定。故所有参与对比的3种模型结合面径向压杆(或径向梁)及切向弹簧数量都取1 600个。3种模型采用埋深22.57 m、水头26.99 m的相同荷载工况。
管片衬砌及二次衬砌的材料参数见表1。结合面径向压杆刚度为(5.98×109/n)kN/m,切向弹簧刚度为(1.94×109/n)kN/m,n为环向压杆数量。模型1不需要输入结合面切向刚度值。管片接头环向拉压弹簧刚度取7.95×109kN/m,径向剪切弹簧刚度取1.73×109kN/m。根据国内外有关研究结果[11,12],管片接头的环向抗弯弹簧刚度在隧道内侧受拉时取4×105kN·m,外侧受拉时取2.4×105kN·m。地基径向抗力系数取7.0 MPa,根据式( 3 )可以计算出地层接触面径向压杆刚度为(5.5×105/n)kN/m,切向弹簧刚度取径向刚度的一半。

表1 衬砌材料参数
2.3 结果对比分析
采用3种模型所获得的双层衬砌、管片衬砌、二次衬砌的单环(幅宽2m)弯矩值(弯矩以衬砌外侧受拉为正),如图5所示,弯矩最值见表2,轴力值(轴力以受拉为正)如图6所示,轴力最值见表3。需要说明的是双层衬砌弯矩和轴力值分别为同一截面管片衬砌、二次衬砌相应弯矩和轴力值之和,表2和表3中双层衬砌、管片衬砌和二次衬砌的最值不一定出现在同一平面上。

图5 三种模型计算弯矩(kN·m)

图6 三种模型计算轴力(MN)

项目双层衬砌弯矩管片衬砌弯矩二次衬砌弯矩最大值最小值最大值最小值最大值最小值模型1478.2-576.41347.39-440.58176.55-186.5模型2516.88-621.31427.46-522.78328.37-318.22模型3639.86-794.02492.33-587.89246.34-286.44
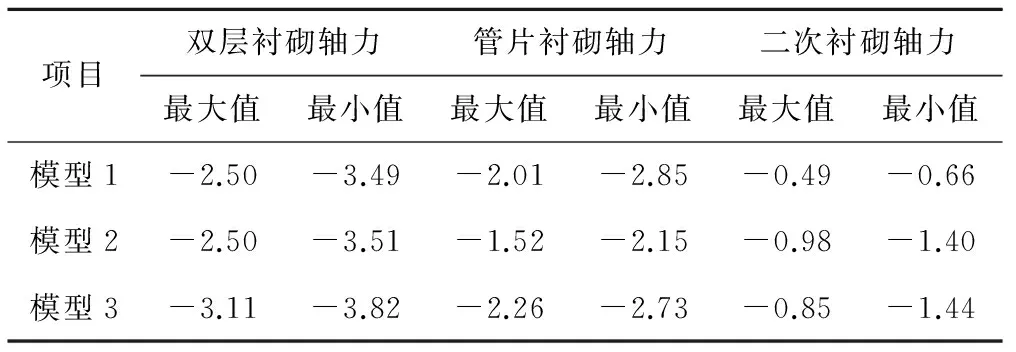
表3 3种模型轴力最值 MN
从图5和表2可见,就3种模型而言,模型3计算分析获得的双层衬砌和管片衬砌的最大正负弯矩值最大,分别为639.86 kN·m、-794.02 kN·m、492.33 kN·m、-587.89 kN·m,其次是模型2和模型1;模型2分析获得的二次衬砌最大正负弯矩值最大,分别为328.37 kN·m、-318.22 kN·m,其次是模型3和模型1。3种模型分析所获得的双层衬砌弯矩分布较平顺,而管片衬砌和二次衬砌弯矩分布在拱顶、拱底和左右拱腰接头处呈现明显波动,其中二次衬砌弯矩分布在上述部位的波动尤其剧烈,如左拱部从86 kN·m波动到275 kN·m。图5(d)为图5(a)中A部位的放大图,由图5(d)可见,模型1在节点处出现弯矩突变,而模型2和模型3无此现象。该突变不同于图5(b)和5(c)中不同节点的数值波动,是指同一节点出现两个不同的弯矩值,原因可能是结合面梁单元同时与管片衬砌和二次衬砌固结,梁单元在传递轴力的同时也在传递弯矩,会在梁与管片衬砌和二次衬砌各自的连接点上产生弯矩分配,且分配的弯矩大小跟结合面单个径向梁单元的抗弯刚度有关。总体上看,采用3种模型所获得的双层衬砌、管片衬砌和二次衬砌弯矩值大小及分布基本一致。
从图6和表3可见,3种模型所获得的双层衬砌轴力值皆为负值(受压)。双层衬砌轴力最大负值同样出现在模型3中,达3 870 kN,而模型2和模型1结果的相对关系并不明显,大致在2 500 kN到3 500 kN之间;管片衬砌轴力最大负值出现在模型1中,与管片衬砌最大正负弯矩值出现在模型3中不一致;二次衬砌轴力最大负值出现在模型3中,达1 440 kN,与二次衬砌最大正负弯矩值出现在模型2中也不一致。总体上看,采用3种模型所获得的双层衬砌、管片衬砌和二次衬砌的轴力大小、分布基本一致。
结合面及地层接触面径向单元受力情况如图7所示。从图7可见,模型1在结合面左右拱腰处出现小范围的径向拉力;模型2在结合面拱顶、拱底和左右拱腰处也出现小范围的径向拉力,且左右拱腰处的径向拉力值较大,这是引起模型2分析所得管片衬砌和二次衬砌弯矩在左右拱腰处发生较大波动的主要原因;模型3在结合面左右拱腰处出现了小范围零值,由于只有模型3结合面设置了只能传递径向压力的弹性压杆,所以只有模型3在结合面左右拱腰处出现小范围零值这一与工程实际较吻合的现象。
由图7(d)~(f)可见,模型1、模型2在地层接触面拱顶、拱底出现大范围的径向拉力并抵消了拱顶和拱底的部分围岩压力效应,这可能是采用模型1、模型2分析获得双层衬砌弯矩绝对值相对模型3较小的原因;模型3在地层接触面拱顶、拱底出现了大范围零值,也是由于结合面采用径向压杆,其原因如前所述。

图7 三种模型结合面及地层接触面径向力(kN)
综上可见:模型1存在结合面径向梁引起弯矩突变、结合面和地层接触面径向弹簧引起径向拉力等问题,且由于只设置了径向梁,未设置结合面切向单元,尽管径向梁在传递径向力的同时也在传递切向力,但其切向刚度依赖径向刚度值和结合面梁的几何尺寸,无法直接设定,模型1结合面梁刚度设置一般优先满足径向刚度,故其切向刚度失真无法避免。模型2在结合面和地层接触面都设有径向和切向弹簧,其径向和切向刚度值可独立设定,但径向弹簧具有受拉功能,会导致结合面和地层接触面出现与真实情况相悖的拉力。模型3采用切向弹簧和径向压杆单元,其不仅能够有效避免弯矩突变,还能解决结合面和地层接触面出现径向拉力的问题,能相对准确模拟双层衬砌盾构隧道各结构的相互连接和力学行为。因此,模型3相对模型1和模型2在分析和模拟双层衬砌力学行为方面更具优势。
3 推荐模型及其应用
由于采用衬砌梁-接头弹簧-结合面压杆弹簧组合模型具有更好的合理性,可将该模型作为双层衬砌力学分析的推荐模型。下面结合该模型研究分析相同外荷载下特定厚度管片衬砌组合不同厚度二次衬砌所表现的双层衬砌力学行为。盾构隧道外径依然为12.5 m,环宽2.0 m,采用“6+2+1”分块型式。管片衬砌厚度取0.45 m,双层衬砌厚度分别取为0.65 m、0.70 m、0.75 m、0.80 m、0.85 m,则对应二次衬砌的厚度分别为0.20 m、0.25 m、0.30 m、0.35 m、0.40 m。计算所得双层衬砌弯矩最大值和最小值以及其对应截面的管片衬砌弯矩见图8(a)和表4,弯矩以衬砌外侧受拉为正,最大值指弯矩最大正值,最小值指弯矩最大负值;双层衬砌轴力最大值和最小值以及其对应截面管片衬砌轴力值见图8(b)和表5, 轴力负值为受压,最大值指轴力的最大压力值,最小值指轴力的最小压力值。


图8 双层衬砌和对应截面管片衬砌弯矩和轴力极值

二次衬砌厚度/cm2025303540双层衬砌厚度/cm6570758085双层衬砌厚度增大比例100%108%115%123%131%双层衬砌弯矩最大值所在截面双层衬砌弯矩/(kN·m)545571603638673对应截面管片衬砌弯矩/(kN·m)491460419373324管片衬砌弯矩占双层衬砌弯矩比例90%81%69%58%48%双层衬砌弯矩增大比例100%105%111%117%123%双层衬砌弯矩最小值所在截面双层衬砌弯矩/(kN·m)-698-721-749-781-813对应截面管片衬砌弯矩/(kN·m)-604-554-494-430-367管片衬砌弯矩占双层衬砌弯矩比例87%77%66%55%45%双层衬砌弯矩增大比例100%103%107%112%116%

表5 双层衬砌轴力最值
由图8(a)可知,随着双层衬砌厚度值不断增大,双层衬砌弯矩最大值和最小值皆呈增大趋势,但最大值和最小值对应截面的管片衬砌弯矩不断减小。由表4可以看出:随着双层衬砌厚度值不断增大,双层衬砌弯矩增长与双层衬砌厚度增长正相关,但双层衬砌的弯矩在管片衬砌和二次衬砌之间的分配比例与两者厚度比例无线性关系;随着二次衬砌厚度值不断增大,管片衬砌承担双层衬砌弯矩的数值和比例快速下降。
由图8(b)可知,双层衬砌轴力的最大值和最小值随着双层衬砌厚度的增长几乎不变,但其各自对应截面管片衬砌的轴力值却略有减小。由表5可以看出:随着二次衬砌厚度值不断增大,双层衬砌轴力增长的比例与双层衬砌厚度增长比例几乎无关,双层衬砌轴力在管片衬砌和二次衬砌间的分配比例与两者厚度比例也无线性关系。双层衬砌轴力最大值所在截面及其轴力最小值所在截面对应管片衬砌轴力占双层衬砌轴力比例基本一致。
4 结论与建议
本文基于荷载结构模式,对比分析国内现有的衬砌梁-接头弹簧-结合面梁模型、衬砌梁-接头弹簧-结合面弹簧模型和衬砌梁-接头弹簧-结合面压杆弹簧组合模型的特征及其合理性。衬砌梁-接头弹簧-结合面梁模型存在结合面及地层接触面出现径向拉力、结合面切向刚度失真、管片衬砌和二次衬砌弯矩突变等问题;衬砌梁-接头弹簧-结合面弹簧模型同样存在结合面、地层接触面出现径向拉力缺陷,不合理的径向拉力会导致管片衬砌和二次衬砌弯矩在左右拱腰发生明显波动;衬砌梁-接头弹簧-结合面压杆弹簧组合模型在结合面和地层接触面径向连接都采用压杆单元,解决了结合面和地层接触面出现径向拉力问题,并可有效避免弯矩突变、结合面切向刚度失真等现象,从而能较准确模拟双层衬砌结构内部的相互作用和荷载传递,是目前相对合理的双层衬砌分析模型。
应用衬砌梁-接头弹簧-结合面压杆弹簧组合模型,对双层衬砌的力学行为进行研究。研究表明:特定荷载下,当管片衬砌厚度一定,增加二次衬砌的厚度,双层衬砌弯矩明显增大,双层衬砌厚度增大对轴力的影响很小;双层衬砌弯矩最大值和最小值对应截面的管片衬砌弯矩值及其所占比例迅速减小,轴力值及其比例减小较少,说明双层衬砌弯矩的增大部分主要转移到了增厚的二次衬砌上;双层衬砌的弯矩在管片衬砌和二次衬砌之间的分配比例与二者厚度比例无线性关系。
参考文献:
[1]Working Group No.2 of International Tunnelling Association. Guidelines for the Design of Shield Tunnel Lining[J]. Tunnelling and Underground Space Technology,2000, 15(3):303-331.
[2]何川,封坤,晏启祥,等. 水下盾构法铁路隧道管片衬砌结构的原型加载试验研究[J]. 中国工程科学,2012,14(10):65-73.
HE Chuan, FENG Kun, YAN Qi-xiang, et al. Prototype Test Study on Mechanical Characteristics of Segmental Lining Structure of Underwater Railway Shield Tunnel[J]. Engineering Sciences, 2012,14(10):65-73.
[3]MOLINS C, ARNAU O. Experimental and Analytical Study of the Structural Response of Segmental Tunnel Linings Based on an In Situ Loading Test. Part 1: Test Configuration and Execuation[J]. Tunnelling and Underground Space Technology,2011, 26(6):764-777.
[4]TEACHAVORASINSKUN S, CHUB-UPPAKARN T. Influence of Segmental Joints on Tunnel Lining[J]. Tunnelling and Underground Space Technology,2010,25(4):490-494.
[5]曾东洋,何川.地铁盾构隧道管片接头抗弯刚度的数值计算[J]. 西南交通大学学报. 2004,39(6):744-748.
ZENG Dong-yang, HE Chuan. Numerical Simulation of Segment Joint Bending Stiffness of Metro Shield Tunnel[J]. Journal of Southwest Jiaotong University, 2004,39(6):744-748.
[6]半谷哲夫. 二次覆工を有するシールドトンネル覆工の力学的特性に関する研究[J]. 鉄道技術報告, 1985, (10):135-142.
[7]村上博智,小泉 淳. 二次覆工された千鳥組セグメントリングの挙動について[J]. 土木学会論文集,1991, (6): 135-142.
[8]张厚美,车法星,夏明耀. 盾构隧道双层衬砌接头荷载试验研究[J].同济大学学报,2001,29(7):779-783.
ZHANG Hou-mei, CHE Fa-xing, XIA Ming-yao. Study on Loads Test of Shield Tunnel Segment Reinforced by Double Linings[J]. Journal of Tongji University, 2001,29(7):779-783.
[9]周济民. 水下盾构法隧道双层衬砌结构力学特性[D]. 成都:西南交通大学,2012.
[10]高松伸行. 二次覆工されたシールドトンネルの軸方向解析モデルに関する研究[D]. 东京:早稲田大学,1994.
[11]滝 英治,依田 真,奥田康三,児玉守広,田中 弘,和田正樹.有筋二次覆工を施したシールドトンネルの軸方向剛性について[J]. 土木学会第44回年次学術講演会講演概要集, 1989,(10):114-117.
[12]田中 弘,山越重志,児玉守広,小泉 淳. 二次覆工を有するシールドトンネル軸方向解析モデルについて[J]. 土木学会第47回年次学術講演会講演概要集,1992,(9):1072-1073.
