基于混合系统模型预测控制的列车自动驾驶策略
2015-05-09王龙生徐洪泽张梦楠段宏伟
王龙生,徐洪泽,张梦楠,段宏伟
1.北京交通大学 电子信息工程学院,北京 100044;2.桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004;3.中国铁道科学研究院 通信信号研究所,北京 100081)
列车自动控制ATC系统在保证列车行车安全、降低列车运行能耗及提高轨道交通系统运营效率等方面发挥着重要的作用。其中,列车自动驾驶ATO系统作为其重要组成部分,是具体实施列车牵引、制动和停车控制的子系统。因此,设计高性能的ATO控制器对于提高列车自动控制水平,改善ATC系统性能具有较高的应用价值[1]。近十年来,各种先进的控制算法都相继用于ATO控制器的设计[2-5],如优化控制[2]、迭代学习控制[3]、H2/H∞控制[4]、自适应控制[5]等。然而,随着对ATO控制性能要求的提高,上述方法缺乏综合考虑非线性模型、多约束及多优化目标问题的能力,导致其在应用上受到限制。
列车在实际运行控制过程中,需要考虑列车安全限速、牵引电机饱和特性和车间最大耦合力等约束条件,同时还需综合考虑运营准时性、节能高效和乘客乘坐舒适度等性能指标。因此,模型预测控制MPC,因具有在控制器的设计过程中能充分考虑系统的输入和状态约束、处理多目标优化问题等优势[6],更适合用于ATO控制器的设计[7, 8]。然而,基于传统模型预测控制CMPC的ATO策略却存在以下问题:(1)对于列车模型中的非线性部分,选择直接忽略或者仅在平衡点附近线性化,所得的列车运行模型误差较大;(2)CMPC在设计动车组列车各车厢分布式牵引力和制动力时,可能会造成拖车在牵引到巡航的转换阶段有制动力输出的情况,增大了列车运行能耗;(3)由于CMPC需要实时在线求解优化问题,会造成控制器设计过程计算量大、硬件实现成本高等问题,极大地限制了其应用范围和应用场合。
本文针对考虑列车运行安全约束及列车非线性运行模型的ATO问题,引入列车运行状态整数变量,提出一种基于混合系统模型预测控制的方案。本文的主要创新点如下:(1)对列车运行阻力进行分段线性化,并引入列车运行状态整数变量,建立基于混合整数的列车多质点运行模型,以保证动车组各车厢牵引力和制动力的正确分配;(2)提出基于混合系统模型预测控制的ATO策略,并应用“输入分块化”技术和显式模型预测控制对算法进行改进,以减少其计算量。前者通过固定一定时间段内的控制量,对输入序列进行分块化,降低控制器的自由度;后者通过离线设计和在线综合的方法减少算法的在线计算时间。
1 模型建立及问题描述
1.1 混合系统列车运行模型

图1 CRH3型动车组编组及单节车厢受力分析
图1为CRH3型8节车厢编组的动车组结构图。第1、3、6、8节车厢(图1中轮子为黑色的车厢)为装备了牵引单元的动力机车,列车每节车厢均装有电空制动单元。动车组列车共n节车厢,定义第i(i=1,2,…,n)节车厢的质量、速度和位移分别为mi、vi和xi;ui为该节车厢的牵引力Fti或制动力Fbi的输出;fri为运行阻力;第i节车厢和第i+1节车厢间的相互作用力为fini(i+1)。考虑第i节车厢受力情况(如图1中第6节车厢所示),根据牛顿运动学定律,动车组的动力学方程组可以表示为

( 1 )
运行阻力和车间作用力可以表示为[9]
fri=mi(c0+cvvi+cavi2)+fai
( 2 )
fini(i+1)=k(xi-xi+1)
( 3 )
式中:c0、cv、ca为运行阻力系数;fai表示由于线路坡度、转弯半径和穿越隧道所产生的附加阻力;k为车钩系统的弹性耦合系数。定义ωi=c0+cvvi+cavi2。
由式( 2 )可知,fri具有明显的非线性特性。本文釆用分段线性化的方法对fri进行处理,从而保证线性化后的曲线有效逼近原曲线的同时,降低了控制器设计和实现的难度。根据CRH3型动车实际运行情况(参数见表1),列车的最高运行速度约为350 km/h,在该运行速度范围内运行阻力的原曲线和分段线性化后的曲线如图2所示。

表1 CRH3型动车组参数

图2 CRH3型列车运行阻力及分段近似曲线
图2中,分三段线性化后的结果已能较好地逼近原非线性曲线。定义j=1,2,3为分段序数,则运行阻力可表示为线性分段函数。
fri=mi(αj+βjvi)+fai
( 4 )
分段所属速度区间和各分段内的参数见表2。

表2 运行阻力分段线性化参数
因此,式( 1 )通过分段线性化和离散化(采样周期Ts=1s)后的状态空间方程可以表示为
( 5 )
式中:系统状态x=[v1v2…vnx1x2…xn]T;输入up=[u1u2…un]T;输出y=[v1x1]T;Apj、Bp、Cp分别由式( 2 )~式( 4 )导出。

式中:1n×n和0n×n分别表示n×n阶单位矩阵和零矩阵。
fAj为与状态和输入无关的仿射项。
综上所述,式( 5 )为由分段参数(Apj,fAj)构成的分段仿射PWA系统。
为了提高动车组列车各车厢牵引力和制动力分配的准确性,引入列车运行状态变量。假设有p辆动车装备了牵引单元,且动车和拖车(拖车数量q=n-p)均装备了制动单元。因此,列车的牵引合力来自于各动车的牵引力,而制动合力来自于动车和拖车的共同制动力。
装备了牵引单元的动车不仅能在牵引过程中提供牵引力,而且能在制动的过程中提供电制动力,所以动车的制动力由电制动力和空气制动力两部分组成。拖车的制动力完全来自制动单元的空气制动力。然而,本文简化了此过程,仅考虑动车制动力的合力。
定义二进制变量δ∈{0,1}表示列车的运行状态,即δ=1表示牵引状态;δ=0表示制动状态。定义动车牵引力和制动力矩阵为
Γt=[Ft1Ft2…Ftp]T
拖车的制动力矩阵为
Γb=[Fb1Fb2…Fbq]T
列车合力
u=[ΓtTΓbT]T
所以列车运行模型( 5 )可进一步表示为
( 6 )
式中:Bt、Bb为相应的牵引力和制动力分配矩阵;Ρi(i=t,b)为由系统状态x和输入u所组成空间的多面体分区[10]。因此,列车运行模型( 6 )为同时包含整数变量和连续变量的混合整数模型。
1.2 列车运行安全约束

( 7 )
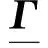
由式( 3 )可知,fini(i+1)可以表示成列车位置的线性组合,所以式( 7 )中的列车速度约束和车钩耦合力的约束可以写成系统状态x(k)的形式。
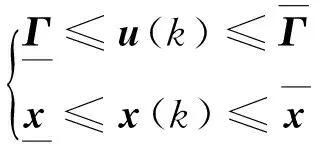
( 8 )

因为各轨道区段内的限速不同,且最大牵引力也是随着列车运行速度变化的,所以牵引力和速度的约束都可以是时变的。
1.3 优化问题描述
根据模型预测控制器的工作原理,设计用于滚动优化的性能指标函数,以直接反映对于列车运营准时性、运行节能高效性及乘坐舒适度等指标的要求。
(1)准时性表现为列车的实际速度-位置对期望速度-位置曲线的追踪精度。该期望曲线是一条提前设计的且满足运营时刻表和节能操纵的曲线[11, 12],其数学表达式为
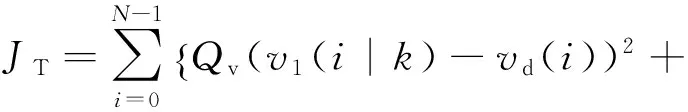
( 9 )
式中:N为MPC的预测步长;状态x(i|k)表示在时刻k之后第i时刻(即k+i时刻)的预测状态;同理y(i|k)、u(i|k)表示第k+i时刻的预测输出和输入;Qv和Qx分别表示速度误差和位移误差的权重。
(2)节能高效表现为使列车在牵引过程和制动过程中的能耗之和最小,其数学表达式为
(10)
式中:Rt和Rb分别表示牵引力和制动力所产生能耗的权重。
(3)乘客乘坐舒适度主要表现为列车加速和制动过程中加速度的变化率不能过快,其数学表达式为

(11)
综上所述,性能指标函数J将由上面3个部分组成,并根据实际的优化目标选择合适的权重Qv、Qx、Rt、Rb、ΔRt、ΔRb。记为系统输入和输出的标准形式。
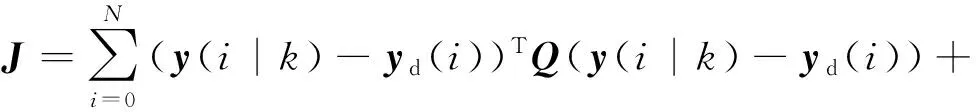
(12)
式中:Q、R为优化权重;yd=[vdxd]T。
2 模型预测控制器设计
模型预测控制器的设计分为两步:(1)通过在线求解的HMPC方法,调节控制器参数及权重,以达到理想的控制效果;(2)基于上述参数,通过输入分块化技术和EMPC重新设计控制器。该方法避免了需要在每个采样时刻对混合整数优化问题进行在线求解,有效减小了计算量,降低了控制器硬件成本,便于在嵌入式芯片或者FPGA上的实现。
基于HMPC的ATO系统总体结构框如图3所示,其中列车动态模型为保持原有非线性属性的原模型,分段线性化模型( 6 )仅用于控制器设计,列车速度和位置可以通过检查单元的传感器测出,目标速度和位置为已知的参考信号。
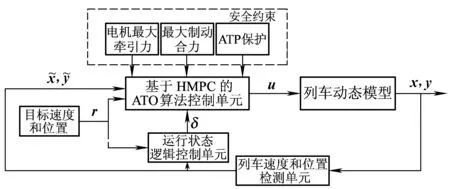
图3 系统控制框图
2.1 模型预测控制
模型预测控制是一种基于模型的闭环、滚动优化控制策略,算法核心为:根据k时刻的系统状态x(k)以及预测模型,构建基于性能指标函数J的优化步长为N的优化问题PN(x(k)),并求其最优解序列U*=[u*(0|k)u*(1|k) …u*(N-1|k)]T,但是仅有k时刻的最优解u*(0|k) 被用于控制器的实现,并在k+1 时刻重复上述步骤,进行反复迭代[6]。
为了便于HMPC控制器的设计,使用文献[13]提出的方法将分段仿射系统转换成混合逻辑动态方程MLD的形式,该形式的问题能被HYSDEL[14]语言所描述,可直接用于Matlab扩展工具箱MPT 3.0[15],计算最优问题的解。式( 6 )和式( 8 )转换为MLD后可以表示为
(13)
式中:z(k)为辅助的连续变量。
综上所述,用于MPC设计的最优问题PN(x(k))将表示为
(14)
为了求解优化问题(14),最小化性能指标函数J将等价于最小化以下标准形式的混合整数二次规划MIQP问题。
(15)
式中:
ΔU=[Δu(0|k) Δu(1|k) … Δu(Nu-1|k)]T
H=R+ΘTQΘ
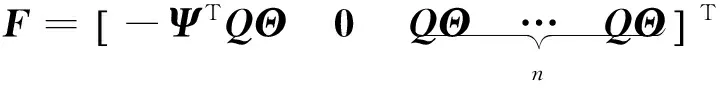
因此,可以通过求解该MIQP问题,得到其最优解ΔU*,此时系统的预测输出为
(16)
Ψ=[CACA2…CAN]T

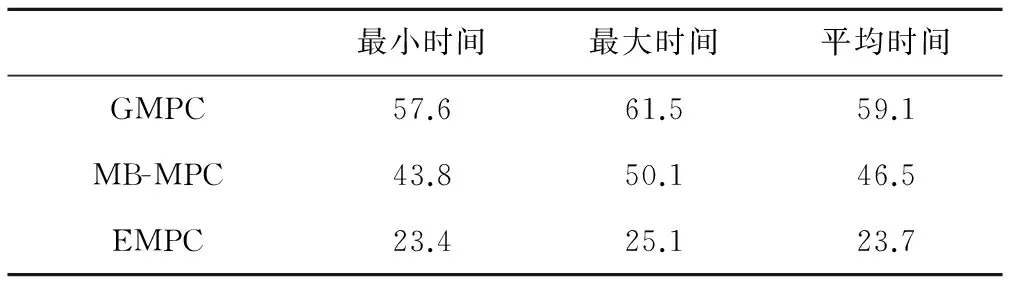
算法中出现的3种步长N、Nu、Nr的选取说明:(1)预测步长N的选取既要足够大,以保证输出效果和控制器的稳定性[16],又不能过大,以免增加算法的自由度,增大计算量,不利于硬件实现。(2)输入步长Nu的选取应该相对小,以减少算法的变量数,减小计算量,其原理是当Nu 对于MPC问题,无论采用在线求解,还是多参数化离线处理的方式,其自由度都是制约计算量的关键因素。本节提出基于“输入移动分块化”的模型预测控制MB-MPC策略,其原理是:将系统控制变量分为M(M 图4 输入分块化策略示意图 “输入分块化”策略的数学形式为 (17) 有时系统需要足够的预测控制时间(Tpred=NTs)以保证控制的性能,在Ts不变的情况下只能增大N,而“输入分块化”策略能在N增大的同时保持Nu基本不变,减小算法的复杂度。 为了进一步减小计算量带来的负担,基于前文在线计算的MPC的参数和权重,重新构建显式模型预测控制器EMPC。该控制器采用离线设计、在线综合的策略,通过将综合控制律的部分由在线计算转换为离线计算,以达到降低在线计算量的目的。其原理为:通过对预测控制在线约束优化问题的分析,离线求解多参数规划问题,对约束状态空间进行分区,并设计各分区的显式反馈控制律;在线优化阶段只需依据系统的当前状态,选择与之相对应的分区的状态反馈控制律[10],并计算控制器输出。这种方法将大量计算转移到离线进行,减小了在线计算的计算量,但是需要更大的内存空间存储分区信息及控制率。 显式模型预测控制率表示为[10] u(k)=Fiθ(k)+fiθ(k)∈Xi (18) 式中:Fi和fi表示在特定多面体集合Xi内的控制器增益;θ(k)为由系统状态、输入和参考信息组成的数量为nr的多面体集合,i=1,2,…,nr。 所以,显式模型预测控制器的实现将分为以下两个阶段:(1)离线计算:在多面体集合θ(k)被分成的nr个集合Xi内,都有与之对应的控制率。该分段控制率不是在线求解MIQP所得,而是通过mp-MIQP求解器离线求解的结果。(2)在线优化:控制器根据当前系统状态和输入判断所属的多面体集合Xi,查找该多面体集合内的控制率,计算当前控制器的输出。 本仿真建立在Matlab 2014a的环境下,运用其扩展工具箱MPT 3.0[15]求解优化问题,硬件平台为主频2.2GHz的Intel酷睿2T6600处理器,3G内存,64位Windows7操作系统的计算机。 仿真选用CRH3型动车组,参数见表1。为了简化仿真而又不失一般性,列车车厢数选取n=3,即首尾动车、中间拖车。同时,考虑乘客重量,在第2、3节车厢的质量上增加5t。车钩最大耦合力为1000kN。仿真中列车动态模型保持原有非线性属性,分段线性化后的混合模型( 6 )仅用于控制器设计。为了验证本文所提ATO控制器的有效性,列车将跟踪一条时变的目标速度曲线(如图5(d)中的虚线所示),该曲线在时刻为200s和600s时发生变化,假设δ(k)只在时刻600s到速度降至30m/s的时间内为0,其他时间均为1。定义不同Cases用于比较不同控制器参数和权重对性能的影响。 Case 1:采样时间Ts=1s,预测步长Np=10,控制步长等于预测步长,权重 R1=0.5×diag([1 1 1]) Q1=10×diag([1 1 1 1 1 1]) Case 2:在Case 1参数的基础上,将输入的权重增大到原来的3倍,即R2=3R1。 Case 3:在Case 1参数的基础上,减小预测步长和控制步长,取Np=Nu=3。 图5 Case1仿真结果 图6 Case1中第一节车厢的牵引和制动力u1 3个Cases的仿真结果分别如图5、图7和图8所示,图6为图5中第一个子图u1的放大效果,其仿真时间、能耗和车钩最大耦合力见表3。图中的前3个子图分别表示每节车厢的牵引力和制动力,其中虚线为牵引力的上界或制动力的下界;最后一个子图的实线表示列车实际运行速度,虚线为目标跟踪速度曲线。 图7 Case2仿真结果 图8 Case3仿真结果 控制器参数输出性能NpRpT/sE/×105kJmaxfin/kNCase110R0672.4534Case2103R0722.1424Case33R0191.9036 Case1仿真结果表明:选择适当的控制器参数和权重时,列车实际速度能跟踪上目标速度,稳态误差几乎为零,并且牵引力、制动力和车钩耦合力都在安全约束范围内。三节车厢的牵引和制动力曲线表明:引入运行状态变量δ(k)后,控制器能够使列车在启动和巡航阶段只有牵引力输出,在制动减速阶段只有制动力输出,验证了列车混合系统模型对于列车多动力分配的正确性。因列车在平衡状态时,其牵引力等于当前所受的运行阻力,且图6中平衡状态时的牵引力和图2中的阻力相对应,验证了列车分段仿射系统的有效性。 由Case2和Case1的对比可知,当增大性能指标函数中输入的权重R后,列车运行的能耗降低了,但是,系统输出却出现了稳态误差,如图7所示。因此,实际情况将根据具体需求调节权重。由Case3和Case1的对比可知,当减小N和Nu时,控制器的计算时间减少,但是此时却不能保证速度跟踪的效果,如图8所示。因此,预测步长应足够大,以确保列车速度跟踪的性能。 本节通过比较使用GMPC、MB-MPC和EMPC3种不同控制器时,列车的实际速度曲线和控制器仿真时间,以验证改进算法对于减少计算量的有效性。 为了获得更准确的仿真时间,对每种控制器进行10次仿真,并记录其最大时间、最小时间及10次的平均时间。GMPC即为前文中Case1的情形;MB-MPC在Case1N=10的基础上,将输入序列以3∶4∶3的比例分成3块;EMPC选取与Case1相同的控制器参数及权重。仿真结果和计算时间如图9和表4所示,图9中大图的虚线为目标速度曲线,实线为列车实际运行速度曲线,小图的内容为在时间250~400 s 内实际速度与目标速度的误差曲线。 图9 GMPC、MB-MPC和EMPC的仿真结果 最小时间最大时间平均时间GMPC57.661.559.1MB-MPC43.850.146.5EMPC23.425.123.7 仿真结果表明:3种控制器基本都能保证列车速度跟踪的控制效果,并且MB-MPC和EMPC的仿真时间明显小于GMPC,其中MB-MPC约为GMPC的80%,EMPC约为GMPC的40%。对于MB-MPC方法,计算时间虽然减少了,但是系统的稳态误差稍微大于其他两种方法;对于EMPC方法,虽然既减少了算法计算时间又保障了稳态性能,但是却需要更多的硬件存储空间用于存储系统输入和状态的分区及各分区的控制率。因此,在实际使用过程中,应根据线路、时刻表等具体内容,以及硬件中CPU频率、存储空间大小等综合因素,从三者中选择更合适的方法。 本文针对综合考虑列车运行安全约束和非线性运行阻力的列车多质点运行模型,利用混合系统模型预测控制,提出一种满足运营准时性、节能和乘客乘坐舒适度的ATO控制策略。通过对非线性运行阻力进行分段线性化,避免了直接对非线性模型设计控制器;建立基于列车运行状态整数变量的混合整数列车运行模型,确保了MPC控制器对于动车组列车各车厢牵引力和制动力的正确分配;提出基于“输入分块化”技术和显式模型预测控制的改进算法,降低了计算复杂性,提高了算法的实用性。数值仿真结果验证了本文所提算法的有效性。 参考文献: [1]唐涛, 黄良骥. 列车自动驾驶系统控制算法综述[J]. 铁道学报, 2003, 25(2): 98-102. TANG Tao, HUANG Liang-ji. A Survey of Control Algorithm for Automatic Train Operation[J]. Journal of the China Railway Society,2003, 25(2): 98-102. [2] CHOU M, XIA X. Optimal Cruise Control of Heavy-haul Trains Equipped with Electronically Controlled Pneumatic Brake Systems[J]. Control Engineering Practice, 2007, 15(5): 511-519. [3]SUN H Q, HOU Z S, LI D Y. Coordinated Iterative Learning Control Schemes for Train Trajectory Tracking With Overspeed Protection[J]. IEEE Transactions on Automation Science and Engineering, 2013, 10(2): 323-333. [4]YANG C D, SUN Y P. Mixed H2/H Cruise Controller Design for High Speed Train[J]. International Journal of Control, 2001, 74(9): 905-920. [5]罗恒钰, 徐洪泽. 基于参考模型的ATO自适应控制算法研究[J]. 铁道学报, 2013, 35(7): 68-73. LUO Heng-yu, XU Hong-ze. Study on Model Reference Adaptive Control of ATO Systems[J]. Journal of the China Railway Society, 2013, 35(7): 68-73. [6]Jan Marian Maciejowski. Predictive Control: with Constraints[M]. Upper Saddle River: Pearson Education, 2002. [7]ZHANG L J, ZHUAN X T. Braking-Penalized Receding Horizon Control of Heavy-Haul Trains[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(4): 1620-1628. [8]王义惠, 罗仁士, 于振宇,等. 考虑ATP限速的ATO控制算法研究[J]. 铁道学报, 2012, 34(5): 59-64. WANG Yi-hui, LUO Ren-shi, YU Zhen-yu, et al. Study on ATO Control Algorithm with Consideration of ATP Speed Limits[J]. Journal of the China Railway Society,2012, 34(5): 59-64. [9]CHOU M, XIA X, KAYSER C. Modelling and Model Validation of Heavy-haul Trains Equipped with Electronically Controlled Pneumatic Brake Systems[J]. Control Engineering Practice, 2007, 15(4): 501-509. [10]Alberto Bemporad, Manfred Morari, Vivek Dua, et al. The Explicit Linear Quadratic Regulator for Constrained Systems[J]. Automatica, 2002, 38(1): 3-20. [11]HOWLETT P G, MILROY I P, PUDNEY P J. Energy-efficient Train Control[J]. Control Engineering Practice, 1994, 2(2): 193-200. [12]WANG Y H, DE SCHUTTER B, VAN DEN BOOM T J J, et al. Optimal Trajectory Planning for Trains-a Pseudospectral Method and a Mixed Integer Linear Programming Approach[J]. Transportation Research Part C: Emerging Technologies, 2013, 29: 97-114. [13]HEEMELS W P M H, SCHUTTER B D, BEMPORAD A. Equivalence of Hybrid Dynamical Models[J]. Automatica, 2001, 37(7): 1085-1091. [14]TORRISI F D, BEMPORAD A. HYSDEL-a Tool for Generating Computational Hybrid Models for Analysis and Synthesis Problems[J]. IEEE Transactions on Control Systems Technology, 2004, 12(2): 235-249. [15]HERCEG M, KVASNICA M, JONES C N, et al. Multi-Parametric Toolbox 3.0[C]// Proceedings of 2013 European Control Conference (Ecc), 2013: 502-510. [16]MAYNE D Q, RAWLINGS J B, RAO C V, et al. Constrained Model Predictive Control: Stability and Optimality[J]. Automatica, 2000, 36(6): 789-814. [17]VALENCIA-PALOMO G, PELEGRINIS M, ROSSITER J A, et al. A Move-blocking Strategy to Improve Tracking in Predictive Control[C]// Proceedings of 2010 American Control Conference, 2010: 6293-6298.2.2 输入分块化策略


2.3 显式模型预测控制EMPC
3 仿真结果与分析
3.1 控制器性能验证



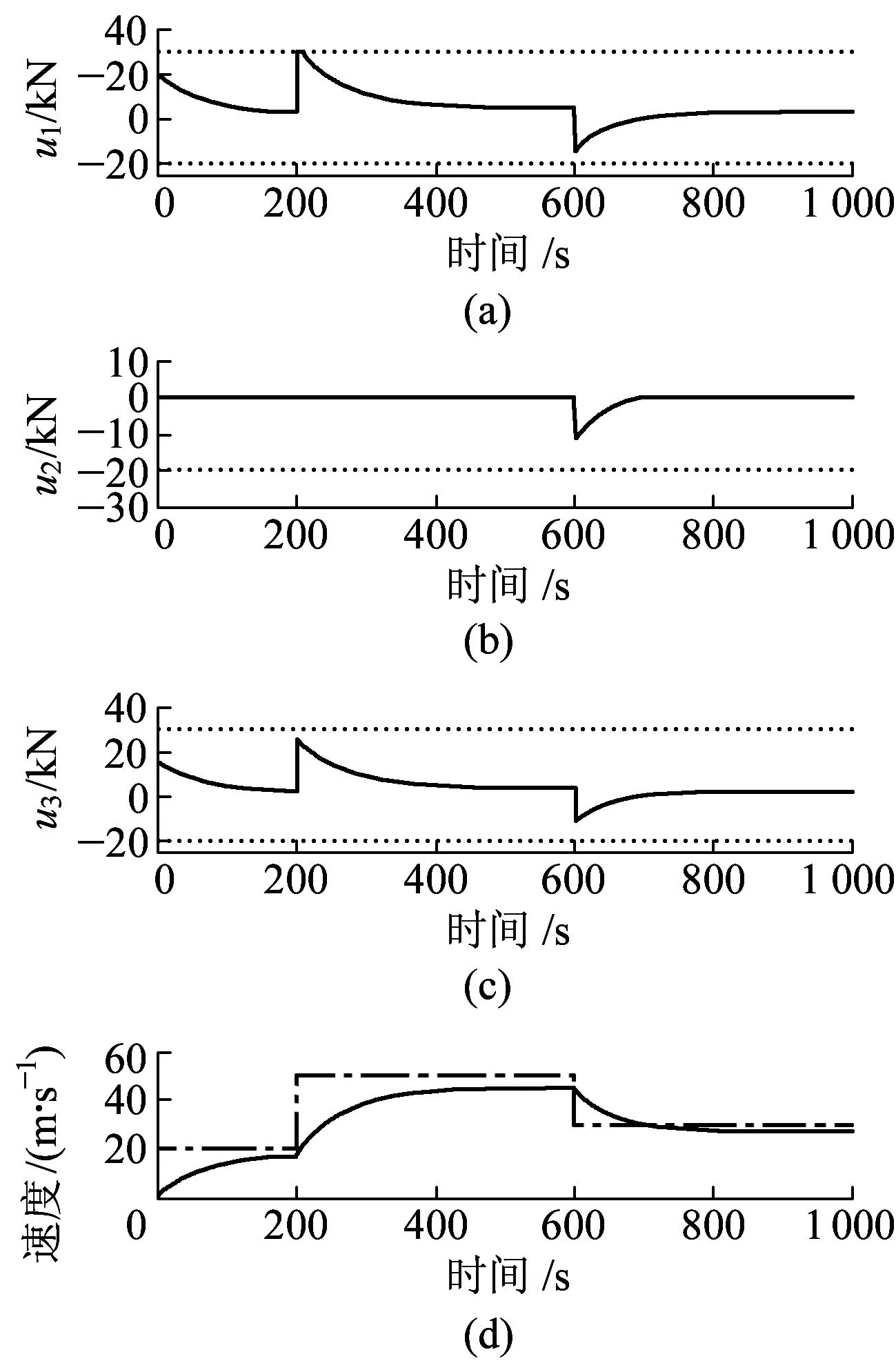

3.2 改进算法的计算时间比较
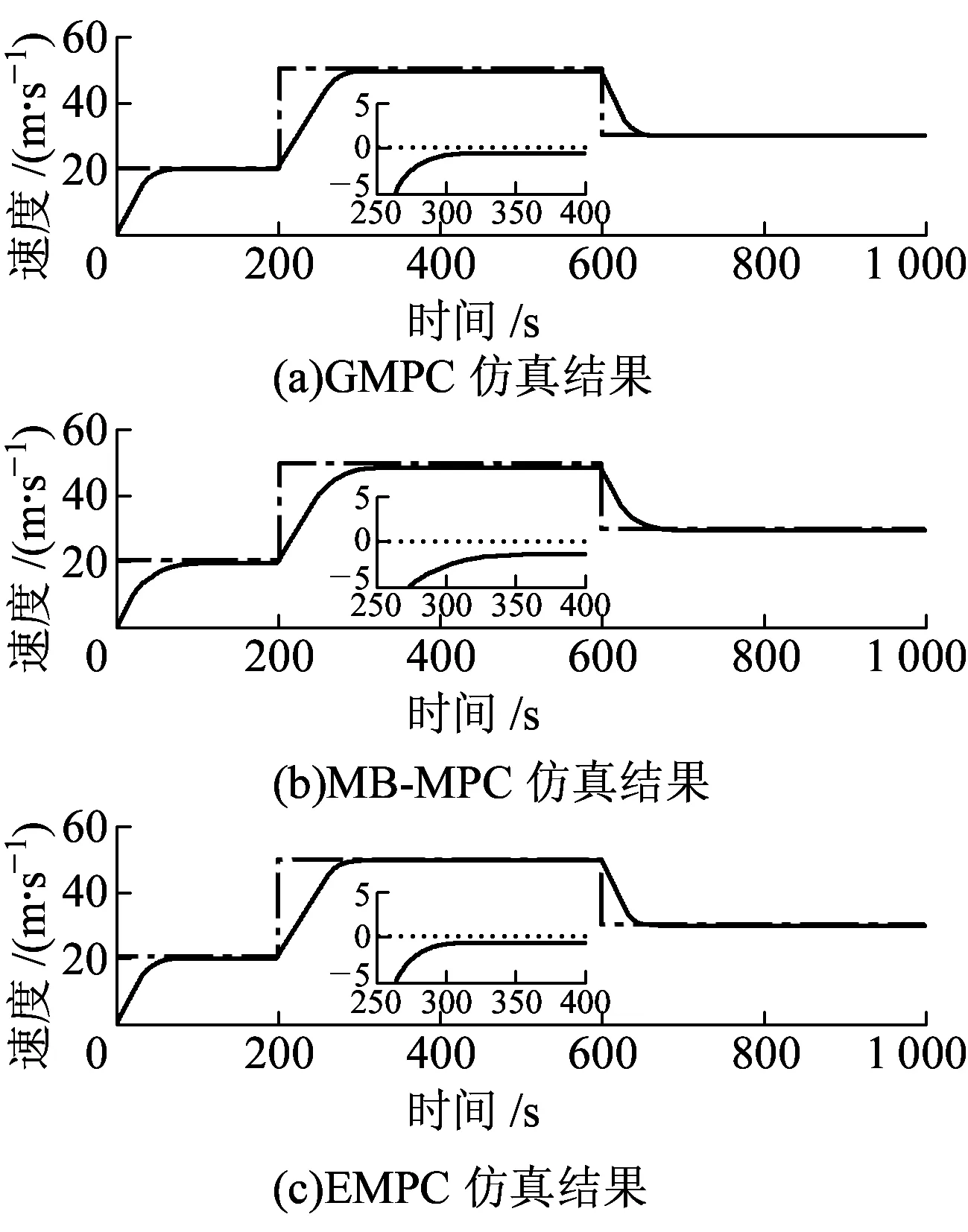
4 结束语
