输油管布置的优化模型
2015-05-09韩慧蓉
杨 青,韩慧蓉
(西安航空学院 理学院,陕西 西安 710077)
输油管布置的优化模型
杨 青,韩慧蓉
(西安航空学院 理学院,陕西 西安 710077)
针对输油管道布置的设计问题,建立了输油管线布置的优化模型。根据两炼油厂到铁路线距离和两炼油厂间距离的各种不同情况,以及附加费用等因素,建立目标函数和约束条件,得出最优方案。
微分法;优化模型;权重
1 问题的提出
现要在铁路线一侧建造两家炼油厂,在铁路线上建一个车站,用来运送成品油。请建立管线建设费用最省的一种数学模型与方法。
问题1.针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提出设计方案。若有共用管线,应考虑共用管线费用与非共用管线费用相同或不同的情形。
问题2.现有两炼油厂A、B,A厂位于郊区,B厂位于城区,A厂到铁路线的距离为5千米,B厂到铁路线的距离为8千米,A厂到城区和郊区的交界处为15千米,B厂到城区和郊区的交界处为5千米。若所有管线的铺设费用均为每千米7.2万元。铺设在城区的管线需增加拆迁和工程补偿等附加费用,为估计附加费用,特聘请公司一、公司二、公司三三家工程咨询公司(其中公司一具有甲级资质,公司二和公司三具有乙级资质)进行了估算。估算结果分别为:21、24、20.(单位 万元/千米)请给出管线布置方案及相应的费用。
问题3.若管线铺设费用分别为输送A厂成品油的每千米5.6万元,输送B厂成品油的每千米6.0万元,共用管线费用为每千米7.2万元,附加费用同上。请给出管线最佳布置方案及相应的费用。
2 模型的建立
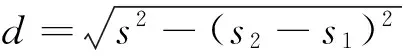
2.1 问题一模型的建立
根据两炼油厂到铁路线距离的不同可分为以下三种情况。
2.1.1 两个炼油厂的连线垂直于铁路线
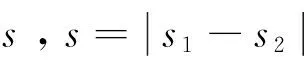
2.1.2 两个炼油厂的连线不垂直于x轴且s1s2
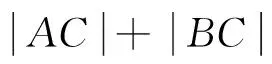
(1)
(2)当输油管道的铺设有公用管线时,设D(见式(1),y)为共用管线与非公用管线的交点,使得建设费用最小,D点可能在如图1中的3个区域内。根据几何的知识和三角形边的知识[1]我们可以计算D点选在区域一和区域二内时的费用都大于选在区域三内的费用,所以D点选址应在区域三(图1中的矩形AEFO)内(或x轴以外的其它三边边界上)。当D点在区域三内时,若s1s2,(如图2)则管线建设费用为即建立管线建设费用最省的目标函数如下:
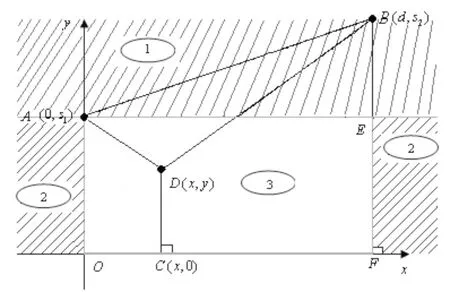
图1 有公用管线时D点的可能位置
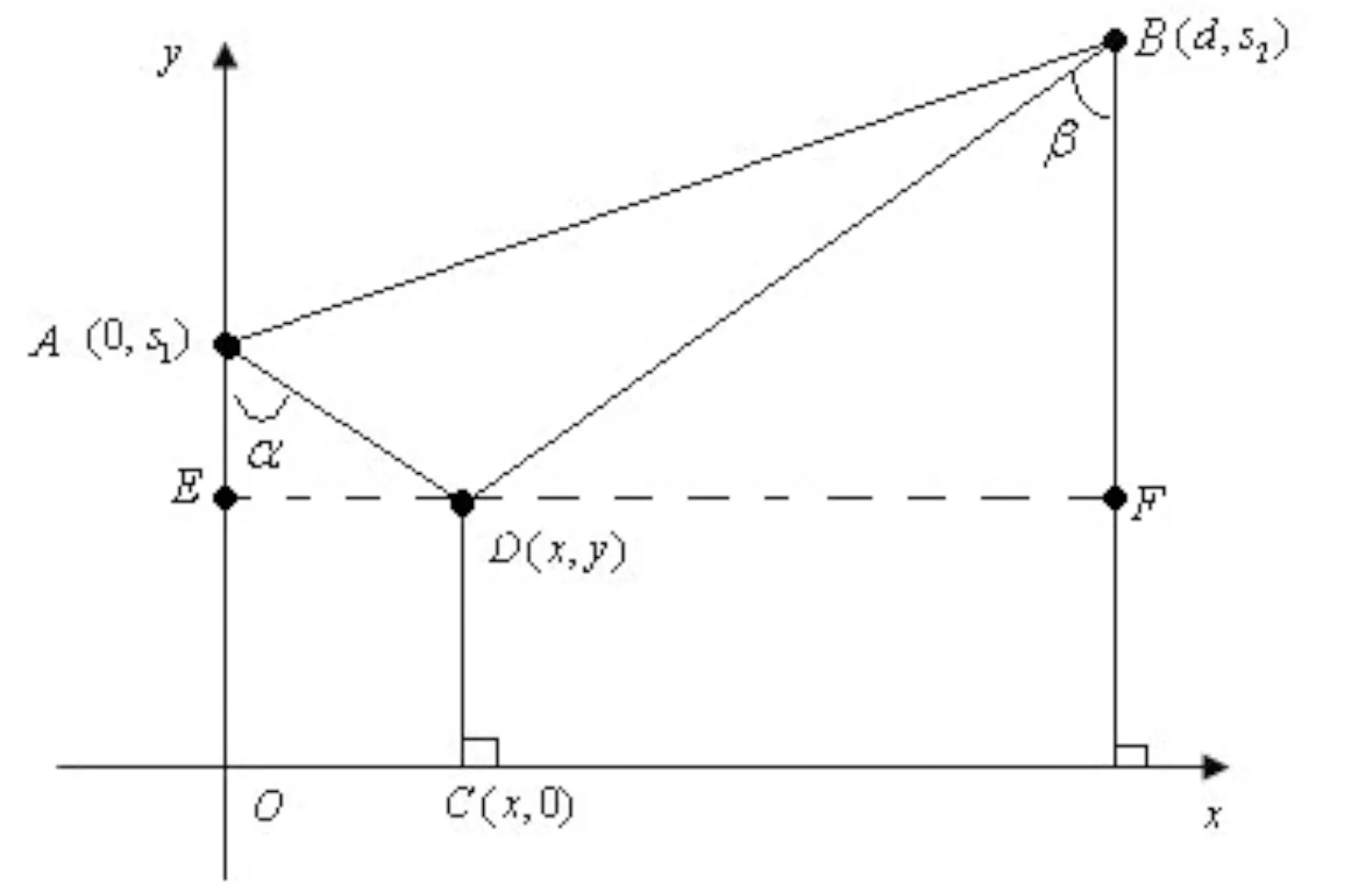
图2 D点在区域三内
(2)
2.1.3 当两个炼油厂的连线不垂直于x轴且s1>s2
可建立同(2)的模型。
2.2 问题二模型的建立
使得建设费用最少,考虑管线铺设费用和城区所需要的附加费用的综合影响。通过分析,车站建在城区的最小总费用大于建在郊区的最小总费用,所以车站只能建在郊区。
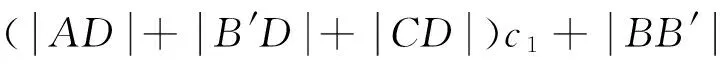
(3)
s.t.y≥0,y2≥0
2.3 问题三模型的建立
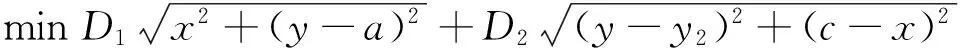
(4)
s.t.y≥0,y2≥0

图3 车站建在郊区时总费用最省的管线布置
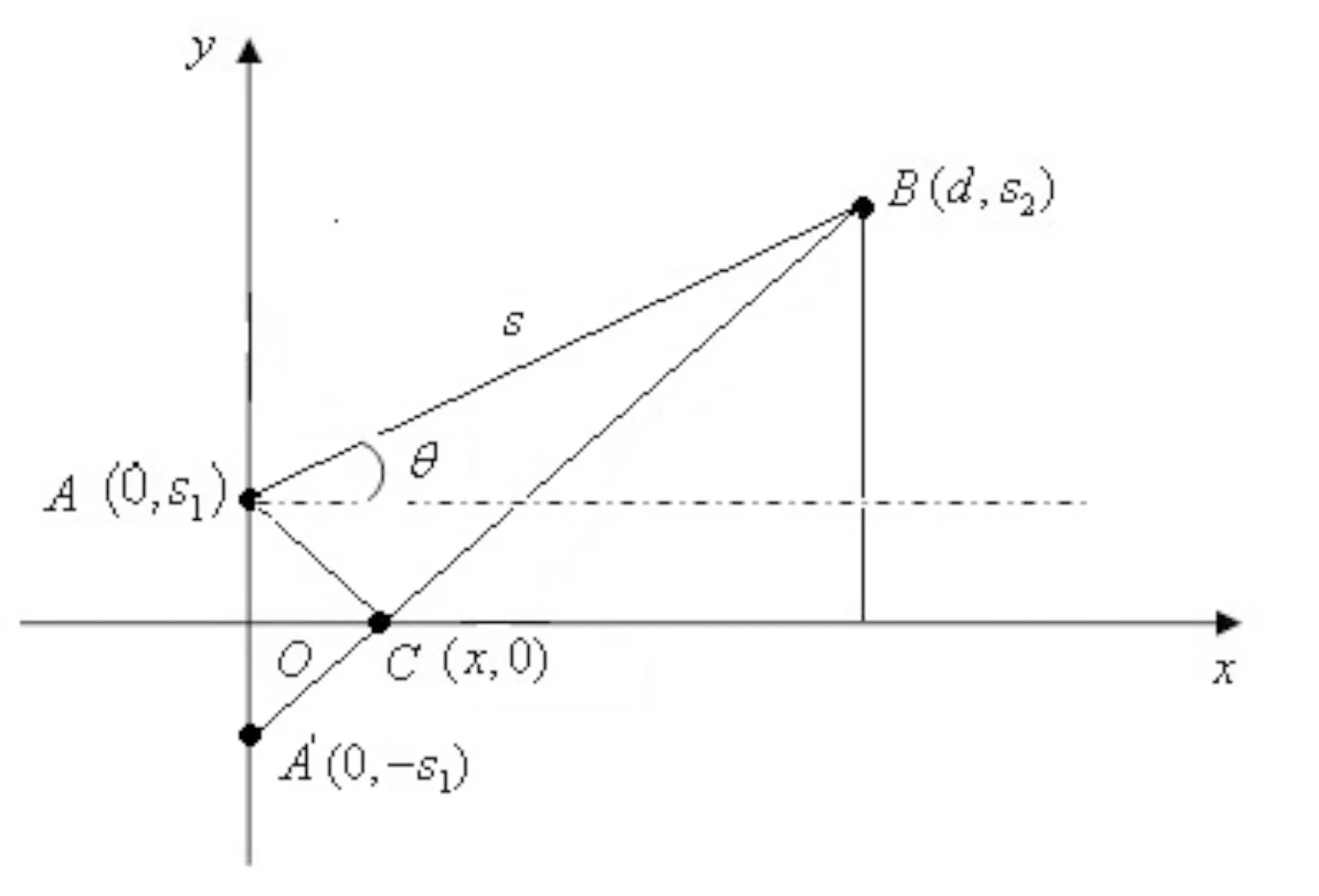
图4 输油管道的布置
3 问题的求解
3.1 问题一的求解
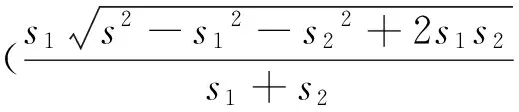
输油管道有公用管线时:
当s1s2时,有。求解,由高数知识可知,利用二元函数偏导数[2,3]先求出驻点,再求最小值。令
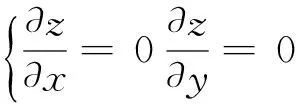
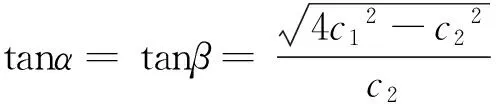
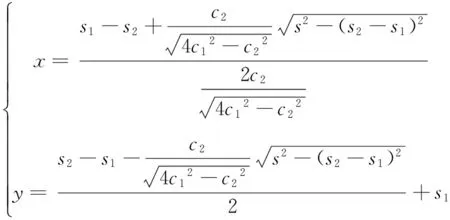

(5)
当s1 所建车站位置坐标为:(x,0),将x,y代入所建目标函数中,得到建设费用最少为: 公用管道与非公用管道费用相同时,即c1=c2,D点坐标为: 最小建设费用为: 3.2 问题二的求解 权重的确定:公司一具有甲级资质,公司二和公司三具有乙级资质,依据资质越高所占权重越大,因此可以取:w1=0.4,w2=0.3,w3=0.3又有g1=21,g2=24,g3=20,从而可得c3=21×0.4+24×0.3+20×0.3=21.6,再将a=5,c=15,l=20,b=8代入(3)式中可得: 总费用的最小值为283.2013万元。并且可以得到x=5.447469,y=1.854901,y2=7.370057。 3.3 问题三的求解 将a=5,c=15,l=20,b=8,c3=21.6,D1=5.6,D2=6.0,c2=7.2代入(4)式中,利用lingo软件解得总费用的最小值为252.4737万元。并且可以得x=6.732103,y=0.1401107,y2=7.282165。 本论文所建立的模型在计算方面采用Lingo软件[4]和Matlab[5]进行求解,可信度高,具有一定的科学性。对于输油管的优化布置具有一定的指导意义。但对于权重的赋值有些主观,应该稍做改进,如考虑的方面能更具体些,建立的模型将更加完善。 [1] 韩中庚.数学建模竞赛—获奖论文精选与点评[M].北京:科学出版社,2007:68-69. [2] 杨启帆.数学建模[M].北京:高等教育出版社,2005:128-130. [3] 胡红亮,赵芳玲.数学建模与竞赛辅导[M].西安:西北大学出版社,2010:85-86. [4] 谢金星,薛毅.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2006:125-126. [5] 苏金明,王永利.MATLAB7.0 实用指南[M].北京:电子工业出版社,2004:74-80. [责任编辑、校对:周 千] Pipeline Layout Optimization Model YANGQing,HANHui-rong (School of Science, Xi'an Aeronautical University, Xi'an 710077, China) In this paper, the problem of pipeline design is proposed and a pipeline layout optimization model is established.The objective functions and constraints are established, and the optimum solution is presented according to the two railway lines from the refinery to refinery and the distance between two different situations, as well as additional costs and so on. differentiation; optimization model; weight 2015-03-25 陕西省科技厅基金项目(2013JM1019);西安航空学院基金项目(2015KY1218) 杨青(1982-),女,陕西咸阳人,讲师,主要从事计算数学、数学模型方面的教学与研究。 TP309 A 1008-9233(2015)03-0061-04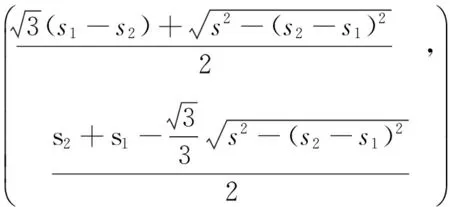

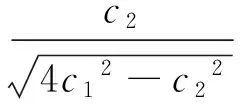
4 模型的评价与改进
