基于SPH方法的淹没水平板消波特性分析

李文博, 王国玉, 张美林, 王永学

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

基于SPH方法的淹没水平板消波特性分析

李文博, 王国玉, 张美林, 王永学

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

应用光滑半立子法(SPH)模拟了规则波对淹没水平板的作用问题，并将波面的数值计算结果与物理水槽中的观测结果进行了对比，表现出较好的一致性。基于数值计算结果与实验数据的比较，探讨了反射系数和透射系数随着相对宽度的变化规律，并给出了淹没水平板周围的流场变化情况，揭示了淹没水平板的消波特性和淹没水平板上下水体的运动规律。

淹没水平板； SPH；数值模拟

0 引言

水平板结构以其结构简单、生产经济、性能优良等优点，逐渐成为一种概念型的防波堤结构，并且关于波浪和水平板作用的相关问题已经展开研究。Mani和Jayakumar[1]、Brossard和Chagdali[2]、Haruyuki Kojima[3]等对下部为立柱或者锚链结构、上部为阀式或板式结构的防波堤开展了研究工作。在后续的研究工作中，部分学者探讨了相对板长[4，5](板长/波长)、相对厚度[4](板厚/水深)、相对水深(水深/波长)、相对潜深(淹没深度/水深)、波陡(波高/波长)、板的倾斜度[6]、板的空隙率、规则波与不规则随机波等因素对水平板结构消波效果的影响。这些研究工作大多基于物理模型试验的方法展开，现有的关于波浪与水平板结构作用的问题一般基于无粘势流函数理论下的边界元和有限体积法。光滑粒子流体动力学方法(Smoothed Particle Hydrodynamics，SPH)自Lucy7]、Gingold和Monaghan[8]提出后，最初应用于研究宇宙天体之间的运动规律，后来被不断延伸应用到相似的满足粒子离散和光滑核函数插值积分这两个基本要求的诸多领域，如电磁场、分子热传导、爆炸力学、穿透冲击力学、计算流体力学以及新近的描述自由水面运动的波浪流体力学等。

关于SPH方法在自由水面流体与简单构筑物的相互作用的数值应用，Todd B和Paul W C[9]应用预报校正的时间积分方法和边界排斥力法的条件设定，模拟了三维情况下溃坝流场与竖直立方柱相互作用过程，并计算了立柱上受到的溃流冲击力。Pourya O等采用在固体结构物附近区域的流体粒子布置加密的形式，变密度地模拟了圆柱在波浪作用下的绕流问题。Fourey G等采用镜像粒子法布置边界粒子条件的方法模拟了溃流作用于弹性竖直方柱以及弹性平板倾倒入水过程中压力场的变化过程，其中结合了有限单元法模拟弹性固相结构物。

基于SPH方法的优点，该文建立了数值波浪水槽，并对波浪作用于淹没水平板的问题开展了研究工作。在初步分析水平板结构消波效果的基础上，描述了淹没水平板周围的流场信息，为深入开展淹没水平板的水动力特性提供了有效的研究方法。

1 控制方程

描述具有自由水面的重力水波传播运动的控制方程一般为连续性方程和动量方程(Navier-Stokes 方程)，其表达式为：

(1)

(2)

(3)

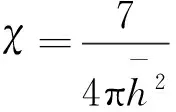
Monaghan[10，11]基于SPH原理，推导出了方程(1)、(2)的如下SPH离散形式：

(4)

(5)

式(5)中的∏ij被称为人工粘度[18]，压力P一般选取Monaghan提出的基于SPH方法模拟自由表面流动问题所应用的状态方程:

(6)

(7)

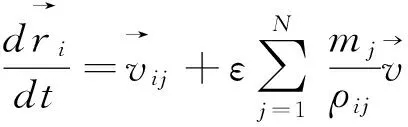
固定边界上的粒子条件设定问题是整个SPH方法中很重要的一部分，往往决定模型建立成功与否，目前仍无较为成熟的假定和理论方法。此前学者多提出修正的意见，一般方法有边界排斥力法、镜像粒子法、固定边界粒子法。该文选取由DalrympleRobertA和KnioOmar提出的固定边界粒子法，在边界处设定两至三层边界粒子，边界粒子参与流体粒子的相互动力作用，但是仅假定速度始终为零。由动量方程形成的积分方程组的数值计算过程采用预报-校正的时间步积分方法。

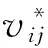
(8)

(9)

将黎曼解的粒子间接触算法与CSPM离散方程结合，式(1)、式(2)可以得到如下形式：

(10)

(11)

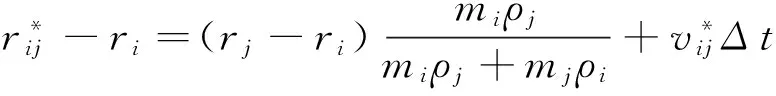
该文采用基于OpenMP工作原理的分块化并行语言编译，在visualstudio环境下用Fortran语言编辑程序运行计算。数值模型采用普通推板式造波形式，设定ω为圆频率，则造波推板上的粒子运动速度可以按下式给出：

(12)

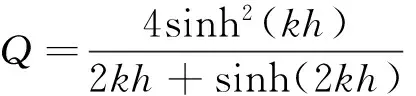
(13)

(14)

式中：x0为消波区域的起始端；l为消波区域的长度；ε、χ为数值实验参数。

2 数值计算域的布置

应用上述SPH方法可建立数值波浪水槽，模拟规则波与淹没水平板的相互作用过程。为了验证数值模拟过程的准确性，在大连理工大学海岸和近海工程国家重点实验室的波浪水槽内进行了二维规则波浪与淹没水平板作用的物理模型试验，试验布置如图1所示。

图1 试验模型布置图

试验中，在淹没水平板的前端放置三个浪高仪，用来记录淹没水平板前的波面变化过程，以分析淹没水平板对波浪的反射作用；在水平板的后端放置一个浪高仪，用来记录水平板后透射波浪的波面变化过程，以分析水平板对波浪的消波性能。试验过程中所需要的物理参数符号见表1。

表1 试验主要波要素

在物理模型试验的基础上，应用SPH方法所建立的规则波与淹没水平板相互作用的数值波浪水槽示意图如图2所示。

图2 淹没水平板的几何模型

数值波浪水槽中造波板位于水槽的左侧，初始位置设定为x=0.20m。波浪水槽总计算域为x×z=15.0m×0.8m。淹没水平板在x轴方向上长度为W=0.50m。数值波浪水槽中，波面观测点的位置与实验中对应的浪高仪所在位置一致。

3 数值计算结果分析

3.1 数值波浪水槽的验证

将该文中，建立的数值波浪水槽所生成的规则波，选取其中的一个波要素为：T=1.20s，h=0.40m，H=0.10m。将波浪数值水槽的沿程不同位置x=3.0m、7.0m和10.0m的波面历时数据与二阶Stokes波理论解进行对比分析，如图3所示。

图3 各测点波面的对比

由图3对比分析可知，SPH数值波浪水槽所生成的规则波的波面历时与二阶Stokes波理论解的波面历时曲线吻合较好。该文建立的数值波浪水槽所生成的规则波浪在沿着水槽向前传播的过程中，能量的沿程衰减和波能的反射叠加效应均可忽略不计，数值波浪水槽性能较好，所生成的波要素可以满足规则波的数值模拟要求。

3.2 水平板前后波面对比分析

为了验证SHP数值波浪水槽的准确性，以便精确模拟波浪与淹没水平板的作用，将数值波浪水槽中的各测点的波面历时曲线分别与物理模型实验中的数据进行对比。图4～图7分别给出了水深h=0.40m、水平板淹没深度ds=0.05m时，波高H=0.10m、周期T=1.0s的入射波浪和淹没水平板作用后，水槽中测点1、测点2、测点3和测点4处波面历时曲线的试验数据和SPH数值模拟结果的对比。

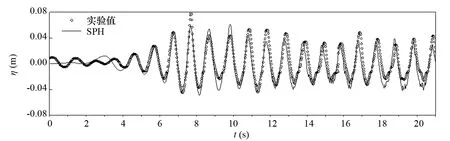
图4 测点1处波面历时曲线对比

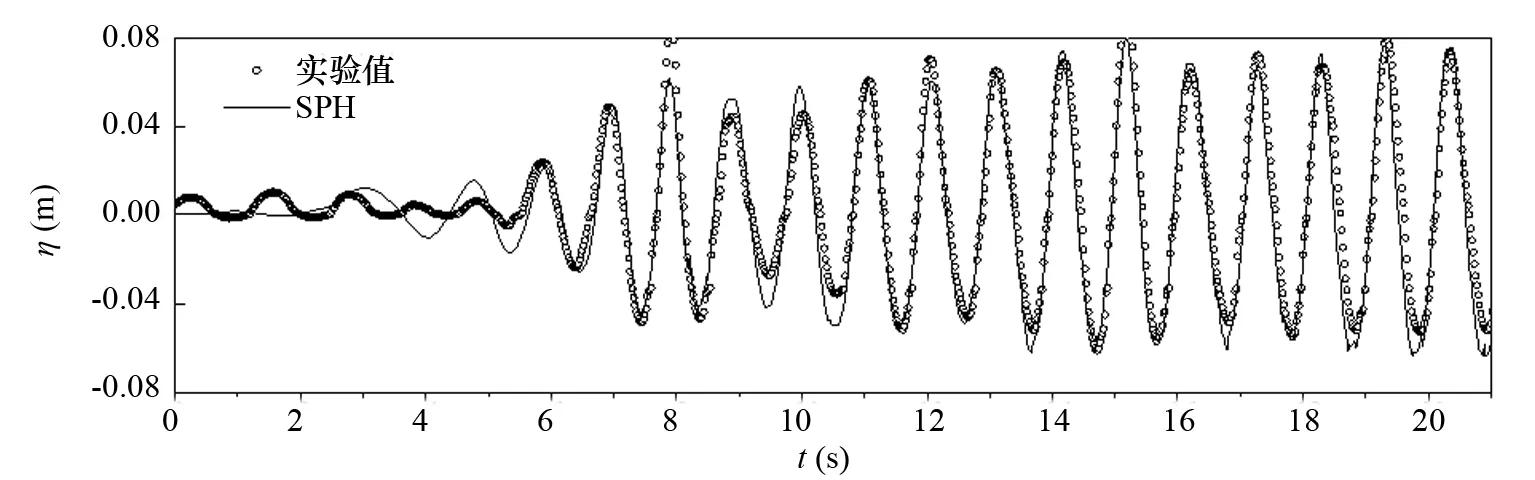
图5 测点2处波面历时曲线对比

图6 测点3处波面历时曲线对比

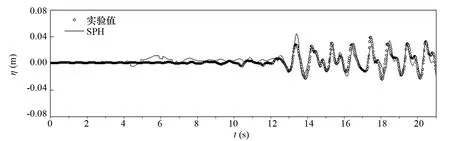
图7 测点4处波面历时曲线对比

由图4～图7的对比结果可以看出，在水平板前后两侧各测点波面历时曲线的SPH数值计算结果与物理模型试验观测结果均吻合良好。在淹没水平板的迎浪侧，测点1、测点2和测点3处的数值计算结果和试验结果均反映出淹没水平板对波浪具有一定的反射作用，而在水平板背浪侧，由于淹没水平板的掩护作用，使得透射波高有较大幅度的降低。

3.3 淹没水平板的消波特性分析

为了分析淹没水平板的消浪性能，将淹没水平板迎浪侧的波面数据通过Goda的两点法进行分离，得到淹没水平板对波浪的反射系数，同时，对淹没水平板背浪侧的波面数据通过上跨零点法统计透射波高，进而得到淹没水平板对波浪的透射系数。图8和图9给出了不同相对淹没深度条件下淹没水平板对波浪反射系数和透射系数随着相对宽度的变化关系试验数据和数值计算结果。

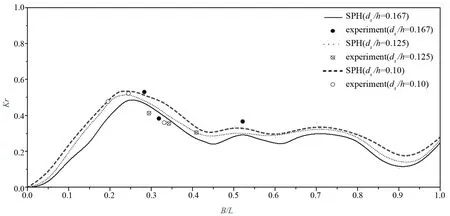
图8 反射系数随相对板宽的变化关系

由图8、图9的比较结果可以看出，数值计算所得淹没水平板对波浪的反射系数和透射系数与实验结果吻合较好，并且数值计算结果表现出一定的周期性变化，这与线性浅水波理论所得的结论一致。反射系数在相对板宽为0.25时，即水平板的宽度为1/4波长时，淹没水平板对波浪的反射作用最强，反射系数到达最大值约为0.5。随着相对宽度进一步增大，反射系数有所降低，且呈现出较弱的周期性波动。在相对宽度小于0.3时，透射系数随着相对宽度的增加迅速降低，且在相对宽度约为0.3时，透射系数可降低至0.4以下，表现出了较好的消波性能。随着相对宽度进一步增大，透射系数也呈现出周期性的波动。

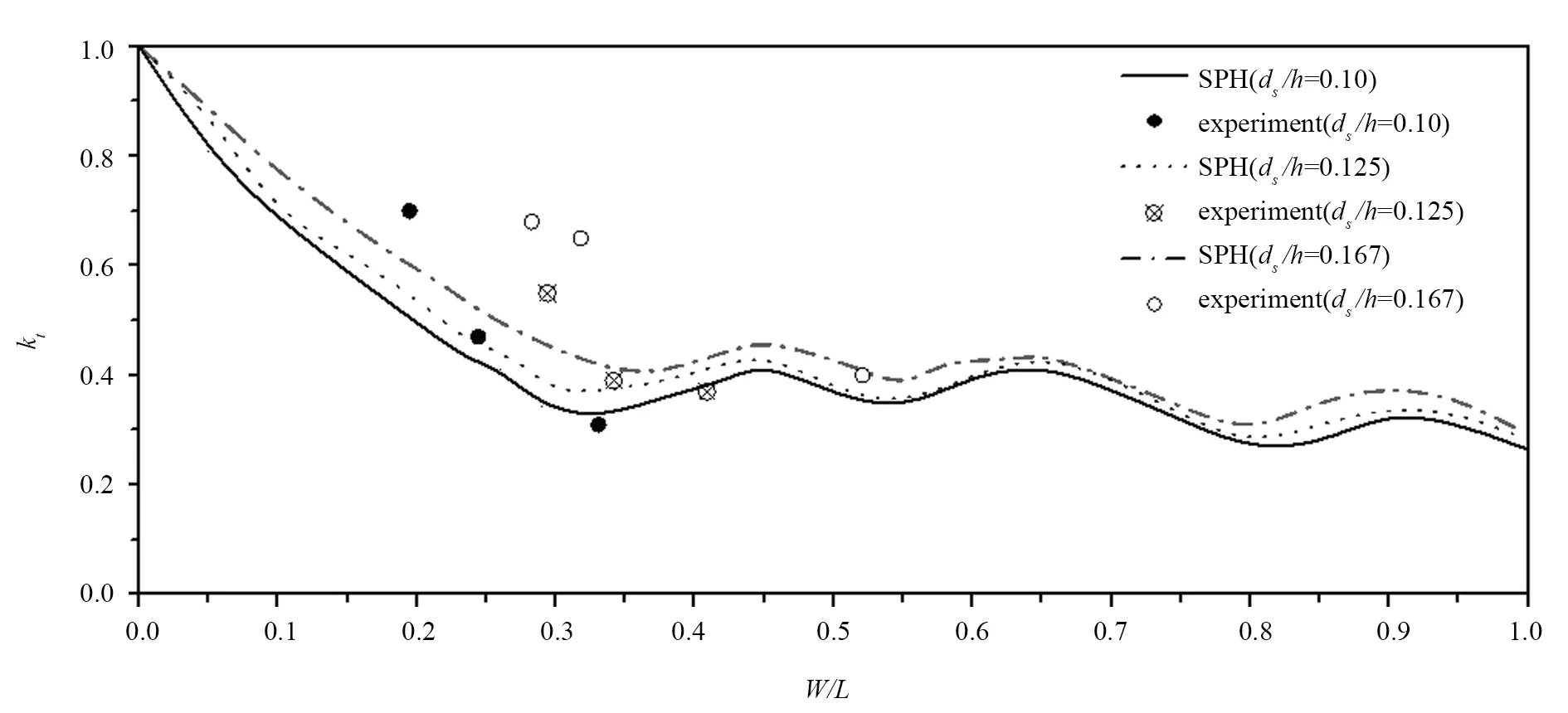
图9 透射系数随相对板宽的变化关系

图10给出了入射波能量传递通过淹没水平板过程中，水平板附近的流场变化情况。入射波在水平板的阻隔作用下发生浅水变形，水平板上侧面产生向右运动的水平流动，到达水平板右端向下产生竖向断面流，进而一部分波能产生涡旋形成紊流。在水平板底部，一部分水质点在虹吸作用下形成与入射波波能传播方向相反的回流运动。这种现象与Kai-Uwe Graw陈述的淹没水深中的单层水平平板在规则波作用下，在水平板与水底边界区域内形成规律性的与波能传播方向相反的脉冲流相符。

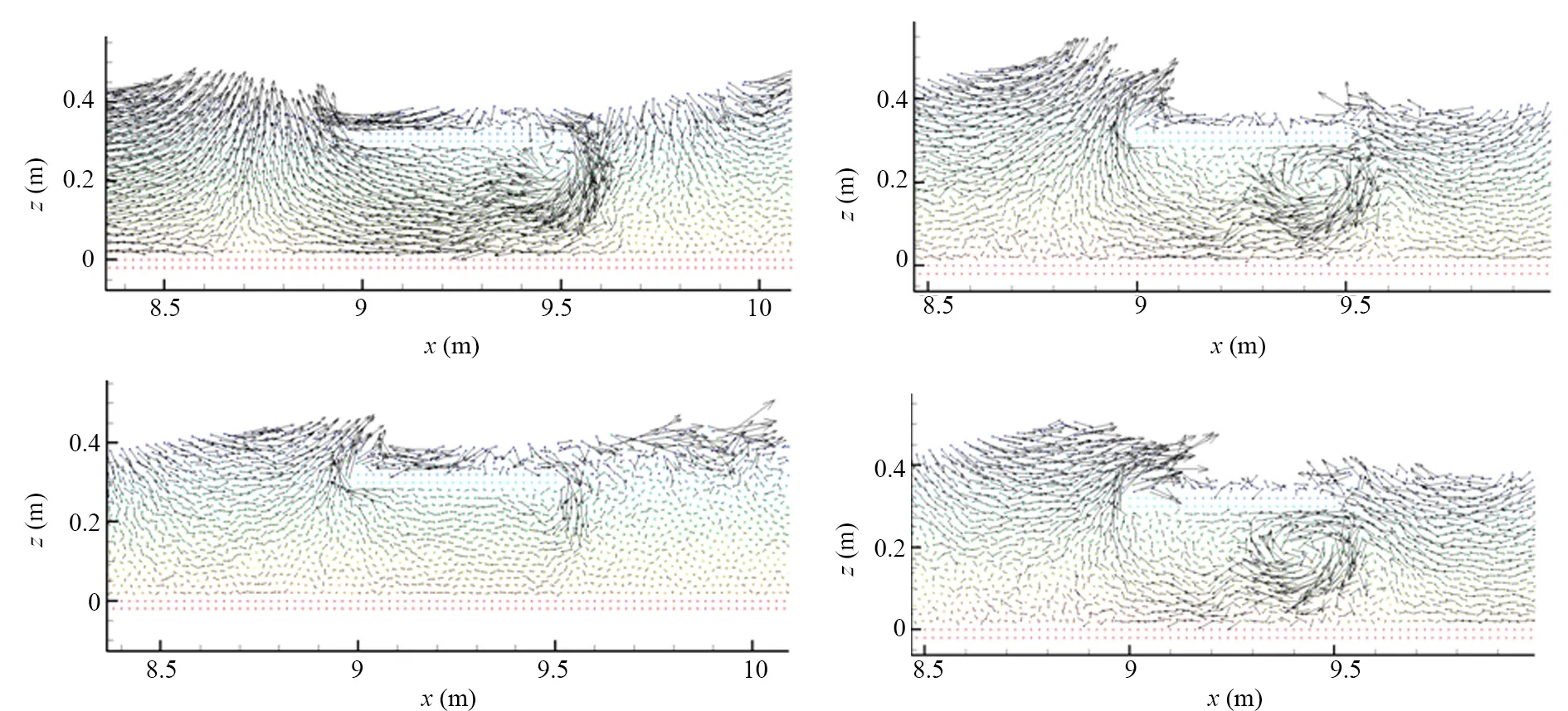
图10 淹没水平板周围的流场变化

4 结论

该文基于光滑粒子法(SPH)建立了二维数值波浪水槽，对规则波浪作用于淹没水平板的问题开展了数值模拟工作。通过与实验水槽测得的水平板前后波面历时曲线的对比，验证了SPH数值波浪水槽的准确性。数值计算结果表明；在水平板的宽度为1/4波长时，其对波浪的反射作用最强，反射系数可达0.5；透射系数在相对宽度小于0.3时，随着相对宽度的增加，迅速降低至0.4左右。此外，由于淹没水平板的阻隔作用，在水平板上方产生向右运动的水平流，到达水平板右端产生向下竖向断面流，进而一部分波能产生涡旋形成紊流，而在水平板底部，在虹吸作用下形成与入射波波能传播方向相反的回流运动。

[ 1 ] Mani J S, Jayakumar S. Wave transmission by suspended pipe breakwater[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1995, 121(6): 335-338.

[ 2 ] Brossard J, Chagdali M. Experimental investigation of the harmonic generation by waves over a submerged plate[J]. Coastal Engineering, 2001, 42(4): 277-290.

[ 3 ] Haruyuki K,Yan Shun guang,Akinori Y,et al. Hydraulic characteristics of a vertical-motioned wave attenuation device with a floating body and submerged horizontal plate[C].Proceedings of The Twelfth International Offshore and Polar Engineering Conference,2002.

[ 4 ] 王科,许旺.平板及立板型式防波堤透射及反射系数研究[J].船舶力学,2010,14(5):487-494.

[ 5 ] Yu Xi ping. Functional performance of a submerged and essentially horizontal plate for offshore wave control: a review[J].Coastal Engineering Journal,2002,44(2):127-147.

[ 6 ] Mikio T. Hydrodynamic forces on submerged plate[C].Proceedings of the Eleventh International Offshore and Polar Engineering Conference,2001.

[ 7 ] Lucy L B, A numerical approach to the testing of the fission hypothesis[J].Astronomical Jounal,1977,82(12):1013-1024.

[ 8 ] Gingold R A, Monaghan J J. Kernel estimates as a basis for general particle methods in hydrodynamics[J]. Journal of Computational Physics,1982,46(3):429-453.

[ 9 ] Todd B Silvester, Paul W Cleary. Wave-structure interaction using Smoothed Particle Hydrodynamics[C]. Fifth International Conference on CFD in the Process Industries CSIRO, 2006.

[10] Monaghan J J. Smoothed particle hydrodynamics [J]. Annual Review of Astronomy and Astrophysics,1992, 30:543-574.

[11] Monaghan J J. SPH simulation of multi-phase flow[J].Computer Physics Communications,1995,87:225-235.

[12] 高睿. SPH强非线性水动力学数值模型的改进与应用[D]. 大连理工大学博士论文，2011，23-31.

[13] 任冰，叶晓文，高睿，等. 波浪与多孔介质结构物相互作用SPH模拟[J]. 海洋工程，2012,30(2):46-53.

[14] He Ming, Ren Bing, Jiang Feng, et al. Simulation of Dynamic Coupling Between Waves and a Free-Floating Rectangular Box by Smoothed Particle Hydrodynamics[C].Proceedings of ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, 2013.

Numerical Simulation with SPH Method on Wave-damping Performance of the Submerged Horizontal Plate

LI Wen-bo, WANG Guo-yu, ZHANG Mei-lin, WANG Yong-xue

(The State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning Dalian 116024, China)

Utilizing the method of Smoothed Particle Hydrodynamics (SPH), the wave dissipating performance of the submerged horizontal plate with finite water depth is simulated. The water surface evaluations of the numerical results are compared with those obtained by the physical model tests with good agreements. The variations of the reflection and the transmission coefficients along with the relative width are presented and compared with the experimental data. The variations of the flow field near the submerged plate are also discussed in detail.

submerged horizontal plate; SPH ; reflection coefficient

2015-04-30

国家自然科学基金创新研究群体项目(51221961)。

李文博(1990-)，男，硕士研究生。

1001-4500(2015)05-0093-08

TV139.2

A