FDPSO总振动与舱室噪声研究

任康旭， 姚 雯， 李泽成， 田 颖

(1. 上海船舶工艺研究所，上海 200032； 2. 中国船舶科学研究中心，江苏无锡 214082)

FDPSO总振动与舱室噪声研究

任康旭1， 姚 雯1， 李泽成2， 田 颖1

(1. 上海船舶工艺研究所，上海 200032； 2. 中国船舶科学研究中心，江苏无锡 214082)

该文以浮式钻井生产储卸装置(FDPSO)为研究对象，建立全船有限元模型，采用有限元法计算了压载和满载工况的总振动。其次利用基于统计能量法的自研软件建立了船舶舱室噪声计算模型，计算结果表明，居住区域的舱室噪声满足MSC.337(91)《船上噪声等级规则》的舱室噪声标准限值要求，但是部分舱室噪声已经接近甚至达到噪声限值。

总振动；船上噪声；舱室噪声；有限元法；统计能量分析

0 引言

浮式钻井生产储卸装置(FDPSO)是浮式生产储卸装置(FPSO)的一种新型浮式海洋工程装备，通过在FPSO 船壳的月池上添加钻探设备，增加钻探功能，集钻探、生产、存储及装卸为一体，具有单独开发油田的能力，从而大大缩短了油田开采的周期，其设计与建造反映了一个国家在海洋油气开发装备上的研发水平。随着海上结构物设计趋向节能、环保、人性化，船舶设计除满足功能使用外，对船上主要生活区和主要工作舱室提出了更加严格的噪声控制要求，船舶噪声不仅会影响舱内各种仪器、设备的正常运行，还会导致某些结构声振疲劳破坏，对长期居住在舱室的船员来说，轻则影响到生活和工作环境的舒适度，重则危害船员身体健康，船员如果长时间处于高噪声环境，容易产生疲劳，降低工作注意力和效率，甚至会间接引发海上事故，并对船员的听力造成永久性的损伤。因此，国际海事组织(IMO)和各国船级社都有明确的噪声标准，尤其在验船时船东对船舶振动噪声有更高的要求。

此外，船体的振动还会引起船上仪器设备的正常使用及造成船体结构的局部疲劳损坏。而且，船体辐射到水下的噪声会对海洋生态环境造成极大的破坏，对海洋生物的生长产生重要的影响。同时，随着船舶及海洋工程技术的不断发展及世界航运业的要求，船舶建造呈现大型化，船舶的动力设备也越来越大型化，作为船舶噪声源的各个设备的噪声控制问题越来越受到船舶设计部门与制造部门的关注。对于高科技与全球经济高速发展的21世纪，人们对舒适性要求越来越高，环保意识越来越强，实现船舶的低振动低噪声设计与制造逐渐成为船舶高性能的重要标志。

1 总振动计算

1.1 计算方法

该文采用有限元法(FEM)作为FDPSO总振动计算的求解方法，有限元法是公认的求解船舶振动问题的有效方法，已经广泛应用于船舶行业。

有限元法的基本思想是里兹法加分片近似。首先，将一个表示结构或连续体的求解域离散为若干子域(单元)，并通过边界上的节点相互连结为组合体。其次，用每个单元内所假设的近似函数来分片表示全求解域内待求的未知场变量。而每个单元内的近似函数，可由未知场函数在单元各结点上的数值和与其对应的插值函数来表达。由于在连接相邻单元的结点上，场函数应具有相同的数值，因而将它们用作数值求解的基本未知量，这样便将求解原来待求场函数的无限自由度问题转换为求解场函数结点值的有限自由度问题。最后，通过和原问题数学模型等效的变分原理或加权余量法，建立求解基本未知量的代数方程组或常微分方程组，求解该方程组便得到问题的解。

1.2 基本方程

结构整体的有限元动力学方程为：

(1)

式中：{r}为结构整体的位移向量；[M]为结构整体的质量矩阵；[C]为结构整体的阻尼矩阵；[K]为结构整体的刚度矩阵；{P}为结构整体的载荷向量。

计算FDPSO总振动时，结构整体的阻尼矩阵和载荷向量均为零，于是得到模态分析的有限元方程为：

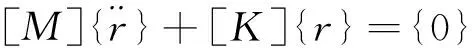
(2)

求解该方程得到的特征值为FDPSO的固有频率，特征向量为FDPSO的振型。

1.3 附连水质量

FDPSO单位长度的附连水质量按式(3)计算。

(3)

式中：mv为垂向总振动时单位长度上的附连水质量；mh为水平总振动时单位长度上的附连水质量；αv为浅水修正系数，与水深和剖面水线半宽之比有关；αh为狭窄航道修正系数，与船舶中纵剖面至岸壁的距离和吃水之比有关；Ki为与振动阶数i有关三维流动修正系数，垂向振动时按船长和船宽之比计算，水平振动时按船长和吃水之比计算；Cv、Ch分别为垂向振动的附连水质量系数、水平振动的附连水质量系数，取决于剖面水线宽度与吃水之比以及浸没剖面面积系数；ρ为水的密度；b为剖面处的水线半宽；d为剖面处的吃水。

图1 总振动计算模型

1.4 计算模型

根据图纸建立FDPSO三维全船有限元模型，总振动计算模型如图1所示，运用有限元软件进行FDPSO总振动计算。该模型除了没有考虑居住区域和钻井模块之外，其余船体部分(板、加强筋等)都根据图纸建模和赋予属性，作为计算船体总振动的模型还是比较适用的。该计算模型的X向正向为船长方向，Y向正向为船的左舷方向，Z向正向为船的高度方向。

1.5 计算结果

计算得到FDPSO各阶振型的附连水质量见表1。附连水质量与振型直接相关，垂向振动的附连水质量远大于水平振动的附连水质量。

采用有限元软件计算得到的FDPSO总振动的固有频率见表2，相应的振型云图如图2～图7所示。

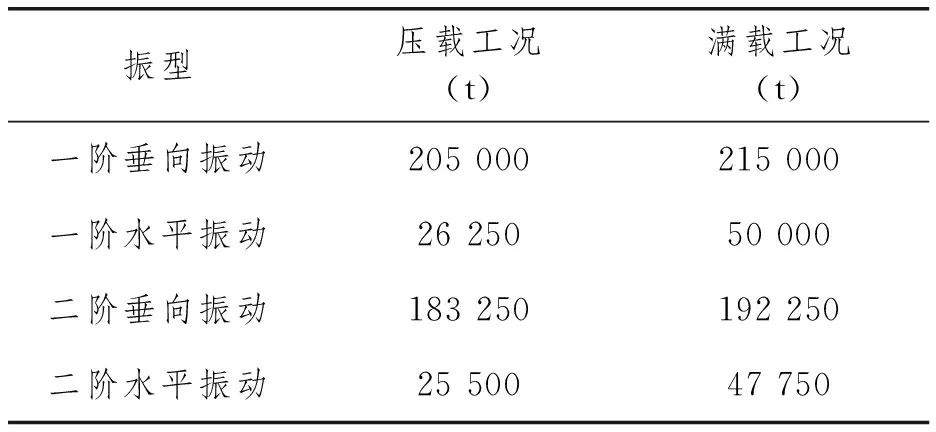
表1 FDPSO的附连水质量

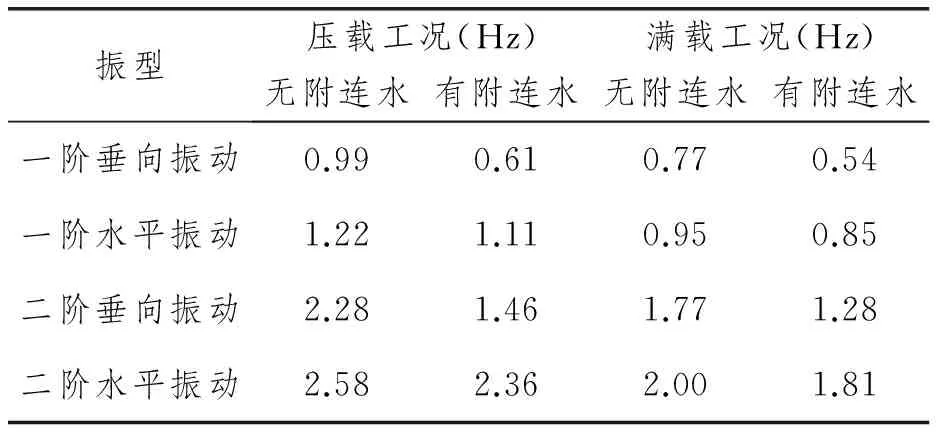
表2 FDPSO总振动的固有频率

图2 等向视图的一阶垂向振动振型 图3 Y向视图的一阶垂向振动振型

图4 Z向视图的一阶水平振动振型 图5 等向视图的二阶垂向振动振型

图6 Y向视图的二阶垂向振动振型 图7 Z向视图的二阶水平振动振型

2 舱室噪声计算

2.1 计算方法

统计能量分析(SEA)是处理中高频结构振动噪声问题的有效方法，因此该文采用统计能量分析(SEA)作为FDPSO舱室噪声计算的求解方法。

统计能量分析方法从能量的角度来分析复杂结构在外载荷作用下的声振响应。统计能量分析方法预报精度受三个主要参数的影响，即模态密度、内损耗因子和耦合损耗因子。对于板、声腔等子系统，模态密度可根据解析公式获得，内损耗因子一般根据试验方法获得，耦合损耗因子可用解析法获得。

中国船舶科学研究中心从二十世纪七十年代开始，致力于统计能量方法在船舶舱室噪声预报中的应用研究，在八十年代末期初步形成了我国船舶舱室噪声的专用数值计算方法，并不断完善船舶舱室噪声理论模型。近年来开发了船舶舱室噪声预报软件，并获得软件著作权，该文采用该软件进行FDPSO舱室噪声计算。

2.2 基本方程

图8 两个子系统能量耦合

对图8所示的两个子系统统计能量耦合模型，可建立如下的能量传递平衡方程：

(4)

(5)

式中：ω为系统的分析频率；P1、P2为时间平均的输入能量；η12、η21为系统间耦合损耗因子；η1、η2为系统阻尼损耗因子；E1、E2为子系统能量；n1、n2为子系统模态密度。

同理，对于由个子系统组成的复杂系统，能量平衡方程扩展可以表示为：

(6)

式中：ω为系统的分析频率；ηi为第i个子系统的内损耗因子；Pi为对第i个子系统输入功率；ni为第i个子系统模态密度；Ei为第i个子系统的系统能量；ηij为两子系统之间的耦合损耗因子。

因此统计能量分析需明确四个参数：内损耗因子、耦合损耗因子、模态密度、输入功率，然后求得各子系统的平均能量，进而求得结构子系统空间或时间的振速、声腔子系统的声压等。

建立能量与响应量之间的关系,由于每个结构或声学的子系统，都具有一个与时间平均和空间平均的振速或声压成比率的稳态能量水平。

对于质量为Mi的结构子系统：

(4)

式中：Ei为第i个子系统的能量；Mi为第i个子系统的质量。

空间声场子系统的声压均方值为：

(5)

式中：Zc为空间声场的声阻抗；Mi为第i个子系统的质量，即空间声场的空气质量。

2.3 舱室噪声限值要求

2014年7月1日起生效的MSC.337(91)《船上噪声等级规则》规定舱室噪声以等效连续A声级表示，舱室噪声结果不得超过相应的噪声限值要求。对于1万总吨以上的船舶，不同部位的舱室噪声限值见表3。

表3 不同部位的舱室噪声限值

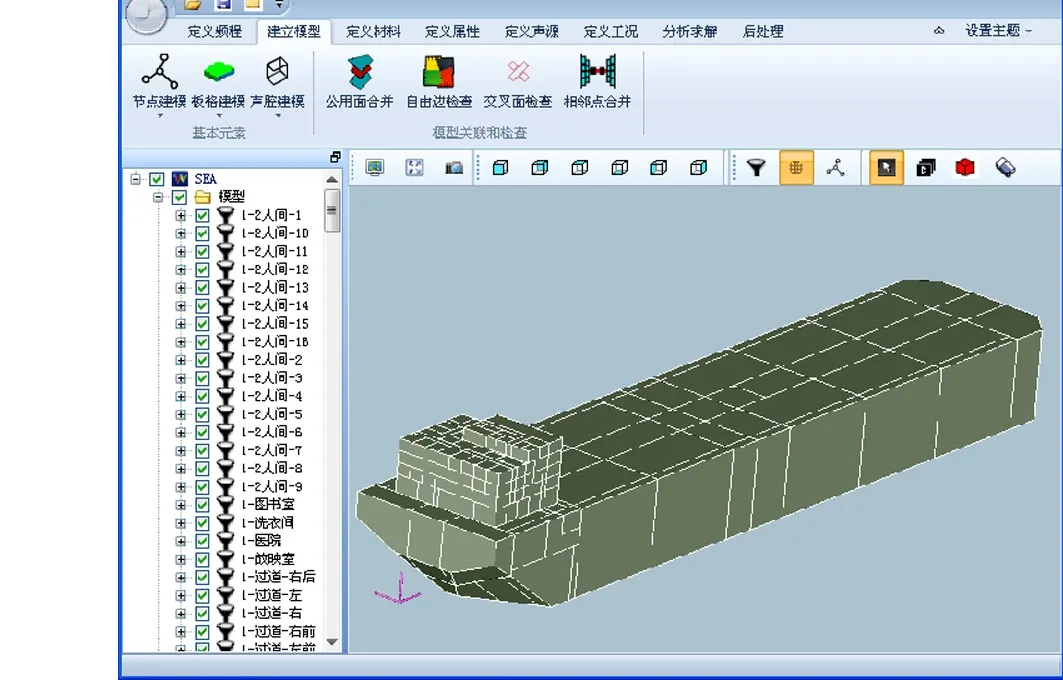
图9 舱室噪声计算模型

2.4 计算模型

由于统计能量法给出的是舱室噪声在空间和频域的平均量，所以统计能量法不能预报舱室子系统内部某个局部位置的声场分布，但能较精确地从统计意义上预报出整个舱室的噪声级。这是统计能量法区别于有限元法的地方，也是统计能量法的优点。所以，统计能量法的计算模型不同于有限元模型，建模时只需把闭合舱室子系统及其与其它子系统的联系表征出来即可，不需要像有限元模型那样精确地描述船体几何特征。

为了计算该船主要舱室的空气噪声，建立全船舱室噪声计算模型，如图9所示，采用统计能量法进行舱室噪声计算。

该文主要关注的是居住区域的舱室空气噪声。居住区域位于船舶尾部，从1甲板到4甲板。柴油发电机组位于船舶中部，离居住区域约110 m，位于居住区域下方的机舱区域噪声源主要有泵舱、机械设备间、空调机室、液压单元间等。

2.5 计算结果

计算得到的全船舱室噪声云图如图10所示，居住区域的舱室噪声具体数值结果见表4～表7，由计算结果可知，FDPSO居住区域的舱室噪声总体上处于良好噪声控制水平，都满足MSC.337(91)《船上噪声等级规则》的舱室噪声标准限值要求。

图10 舱室噪声计算结果云图

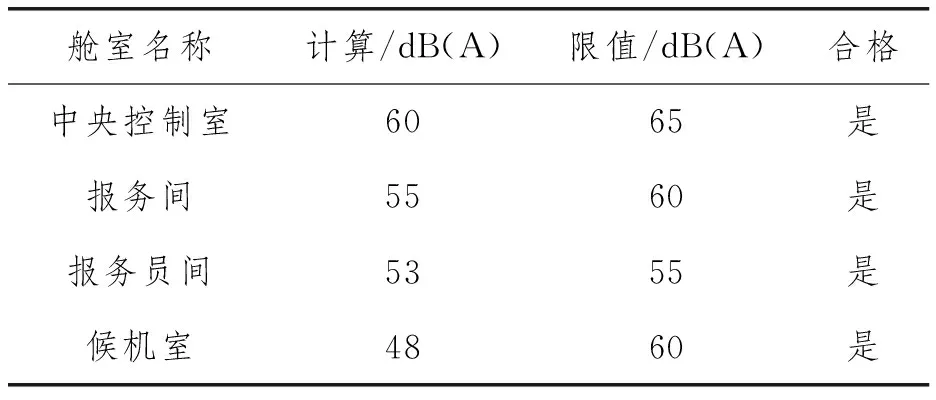
舱室名称计算/dB(A)限值/dB(A)合格中央控制室6065是报务间5560是报务员间5355是候机室4860是

表5 3甲板的舱室噪声计算结果

表6 2甲板的舱室噪声计算结果

表7 1甲板的舱室噪声计算结果

3 结论

该文首先建立FDPSO全船有限元模型，采用有限元法计算了压载和满载状态下的总振动，压载状态下附连水质量对总振动的影响比满载状态下更大，垂向振动的附连水质量远大于水平振动的附连水质量。其次建立FDPSO全船统计能量分析模型，采用统计能量法计算了主要居住舱室和工作舱室的空气噪声，计算结果表明该船居住区域的舱室噪声满足MSC.337(91)《船上噪声等级规则》的船上噪声标准限值要求，但是部分舱室噪声已经接近甚至达到噪声限值。

[1] IMO A.468 (Ⅻ). Code on noise levels on board ships[S]，1981.

[2] MSC 337(91). Code on noise levels on board ships[S]，2012.

[3] 姚德源，王其政. 统计能量分析原理及其应用[M]. 北京：北京工业大学出版社，1995.

[4] 李泽成. 船舶舱室噪声预报方法分析与评估计算[T]. 中国船舶科学研究中心科技报告，2013.

[5] 李泽成，吴文伟. 船舶舱室声学设计指导性文件[T]. 中国船舶科学研究中心科技报告，2014.

[6] 吴文伟，殷学文. 大型油船舱室噪声评估与控制[J]. 船舶力学，2014，18(12)：1524-1533.

Research on Global Vibration and Cabin Noise for FDPSO

REN Kang-xu1, YAO Wen1, LI Ze-cheng2, TIAN Ying1

(1. Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China 2. China Ship Scientific Research Center, Jiangsu Wuxi 214082, China)

Global vibration and cabin noise on Floating Drill Production Storage and Offloading (FDPSO) are researched in this paper. Firstly, based on finite element method, whole ship model is build to calculate global vibration. Secondly, based on statistical energy analysis theory, a numerical model is build to compute ship cabin noise. The evaluated results show that cabin noise in accommodation space is satisfied for noise limit requirement in MSC.337 (91) “Code on noise levels on board ships”, but there are some cabin noises approach to the upper limit.

global vibration; onboard ship noise; cabin noise; finite element method; statistical energy analysis

2015-03-28

任康旭(1982-)，男，工程师。

1001-4500(2015)05-0054-07

U69

A