基于多项式拟合的S型加减速曲线在芯片键合机工作过程中的应用

刘 静，何 田

(无锡派图半导体设备有限公司，江苏无锡 214125)

自20世纪末以来，随着科技进步以及照明产业的发展，LED封装行业也不断地进行着技术革新。如今的封装设备以速度和精度作为主要的性能指标，各厂家在这方面的竞争愈发激烈。LED芯片键合机作为封装过程中不可或缺的设备之一，在此领域同样面临着类似的问题，如何提高LED芯片键合机的速度和精度成为该行业厂家必须面对的重要问题［1］。调研显示，市场上已经出现了固晶周期为160ms的全自动LED芯片键合机，这意味着摆臂式芯片键合机的固晶臂的旋转运动频率达到了每秒钟6～8次，其末端的峰值角速度和峰值加速度分别达到了 163.85rad/s和13 995rad/s2，而固晶臂末端的峰值切向加速度也达到了2 100m/s2，相当于 210 个重力加速度［2－3］。这种情况下，如何保证固晶臂运动的平滑及降低运动过程中及运动结束后的振动成为了运动控制的首要问题。众所周知，运动部件的运动轨迹曲线与运动的最终效果密切相关，因此笔者在对芯片键合机进行运动分析的基础上提出了新型S型加减速曲线。

1 摆臂式芯片键合机关键部件运动分析

摆臂式芯片键合机的关键零部件是固晶臂(也称摆臂)及其驱动机构。固晶臂作为机械手是完成固晶环节的最终执行机构。固晶臂在其驱动机构的驱动下，完成竖直方向的直线运动和绕Z轴的旋转运动，其运动示意图如图1所示。

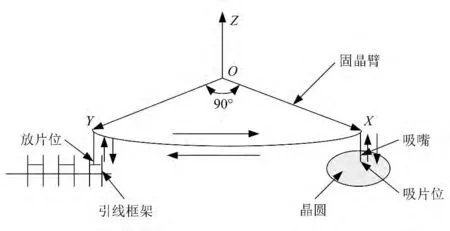
图1 摆臂式芯片键合机固晶臂的运动示意图

如图1所示，固晶臂在旋转电机及直线电机的驱动下完成耦合的直线运动及旋转运动，实现在吸片位从晶圆上将芯片“拾起”然后旋转90°(或180°)在放片位将芯片放入引线框架(垂直或水平框架)的料碗中。运动过程中，固晶臂在竖直方向直线运动的速度及加速度相对于绕Z轴旋转运动的角速度及角加速度而言，要求并没有后者苛刻，绕Z轴的高速旋转运动及快速启停是固晶臂末端产生振动的主要原因。

2 传统加减速曲线分析

图2所示为传统梯形加减速曲线的位移、速度、加速度、加加速度示意图。其位移、速度、加速度及加加速度的曲线皆有突变点，如果将此类运动曲线作为运动控制曲线，应用到固晶臂的运动控制中去，在固晶臂运动过程中及运动结束时必将产生柔性冲击及振动，这将严重影响LED的加工质量。

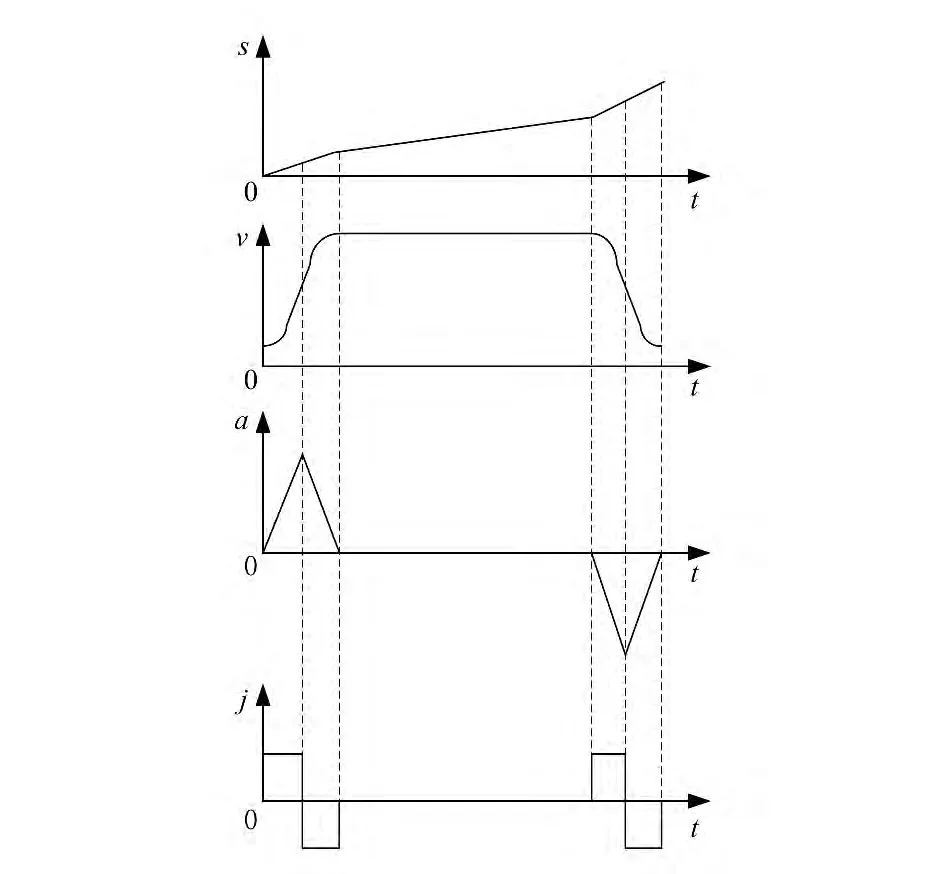
图2 梯形加减速曲线的位移、速度、加速度、加加速度示意图

3 新型S型加减速曲线的提出

对于一些复杂的运动或者计算，很难用理想的函数进行表达或计算得到理想的数值，如全自动LED芯片键合机的加减速运动控制的计算［4－5］。在长期的工程实践过程中，人们积累出了一些经验和方法，即通常在数值计算过程中利用相似函数或者函数拟合的方法去对理想函数进行逼近，以求解其近似数值的方法来解决具体工程问题。

根据高等数学知识可以知道，任何复杂的函数都可以用多项式以简单的加、减、乘的方式进行展开，展开后的多项式可以方便简单地进行数值计算。展开后的多项式的数值解的准确度足以满足工程实践需求。例如，有一函数f(x)在区间(a，b)内(x0在该区间内)具有(n+1)阶的导数，则对任意x∈(a，b)，有如下关系式:

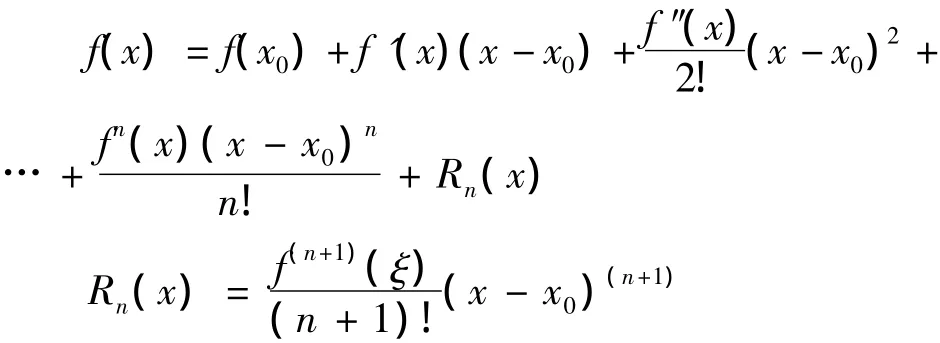
式中:ξ为x0到x之间的某个值。

根据多项式定理，假设某一具体工程问题的计算表达式为:

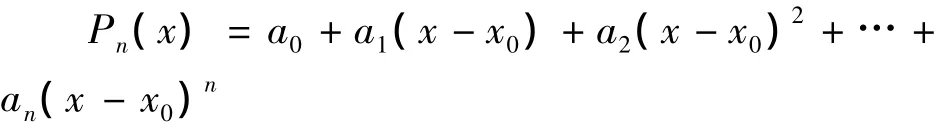
利用多项式展开、逼近的方法可以将任何复杂的理想函数进行近似，在展开过程中，可以略去一些高次的多项式。当然，根据工程计算精确度的要求，多项式展开的次数越高，其对理想函数的近似也就越接近，最终计算得到的数值也就越准确。

4 基于芯片键合机运动控制曲线的五次多项式拟合及应用

从文献［4］、［5］可知，前人已有用三次、四次多项式拟合S型加减速曲线的，但是三次、四次拟合出的多项式的计算结果在解决LED芯片键合机高速度与高精度矛盾问题时往往不能得到较好的结果，原因是三次或者四次多项式拟合出的速度和加速度曲线仍然存在着突变部分。笔者用五次多项式拟合的方法对固晶臂的运动控制曲线进行逼近，构造的函数如下:

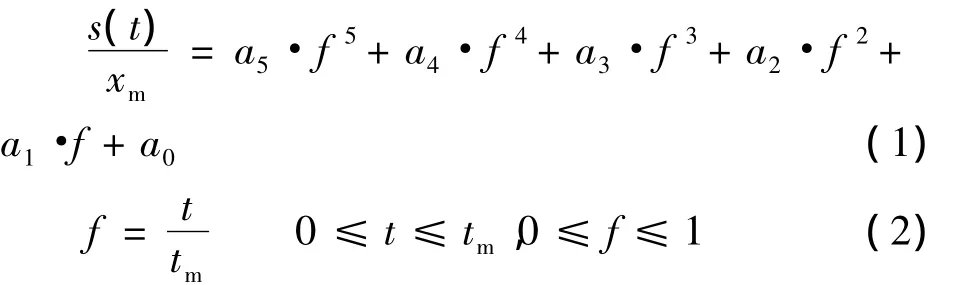
式中:xm为系统设定的总位移(可以是直线位移或者角位移);t为运行过程中的某一时间点;tm为系统设定的加减速运动过程总时间;a0～a5为待定参数。

根据运动学的相关知识可以列出速度、加速度及加加速度与位移之间的关系式。

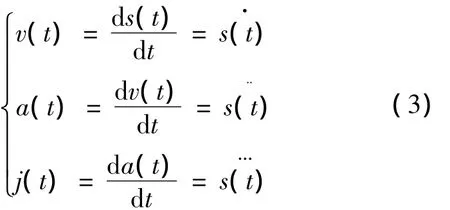
式中:v(t)为速度函数;a(t)为加速度函数;j(t)为加加速度函数。

将式(3)代入式(1)中，整理得到如下关系式。

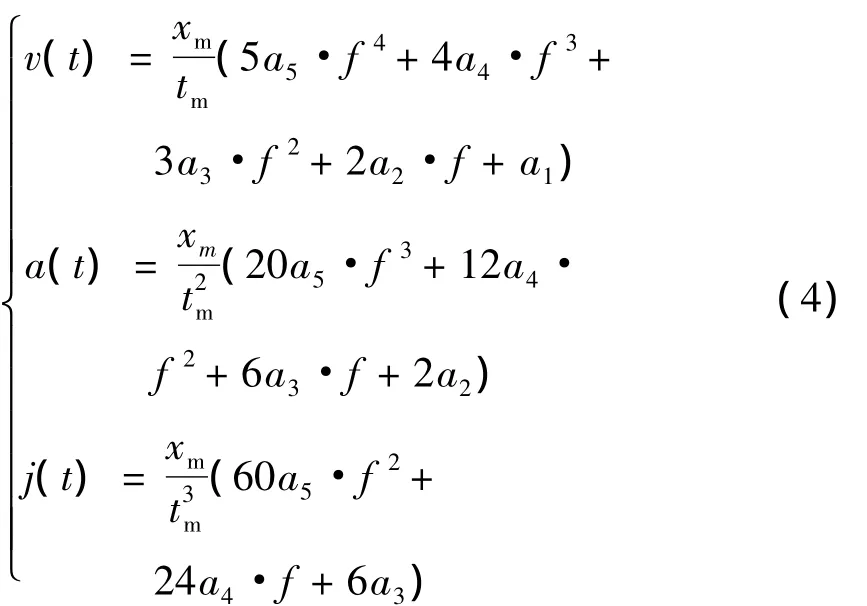
此时，需要约束条件才能解出待定参数，根据LED芯片键合机的运动情况，可以知道如下运动约束条件。

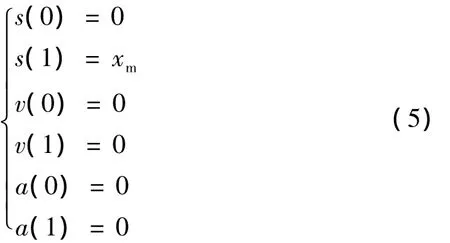
将式(5)代入式(4)即可解出各个待定参数，从而可进一步解出位移(或角位移)函数、速度(或角速度)函数、加速度(或角加速度)函数、加加速度(或角加加速度)函数。

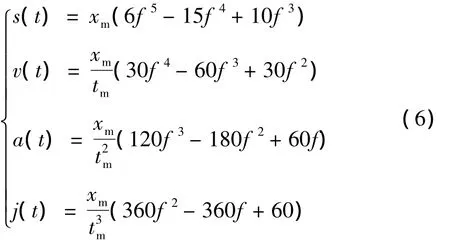
式(6)即为确定的关于五次多项式拟合的S型加减速曲线，假设某一型号的LED芯片键合机固晶臂旋转运动的加减速时间tm=36ms，旋转角位移xm=π，便可以得到如下具有针对性的运动表达式。

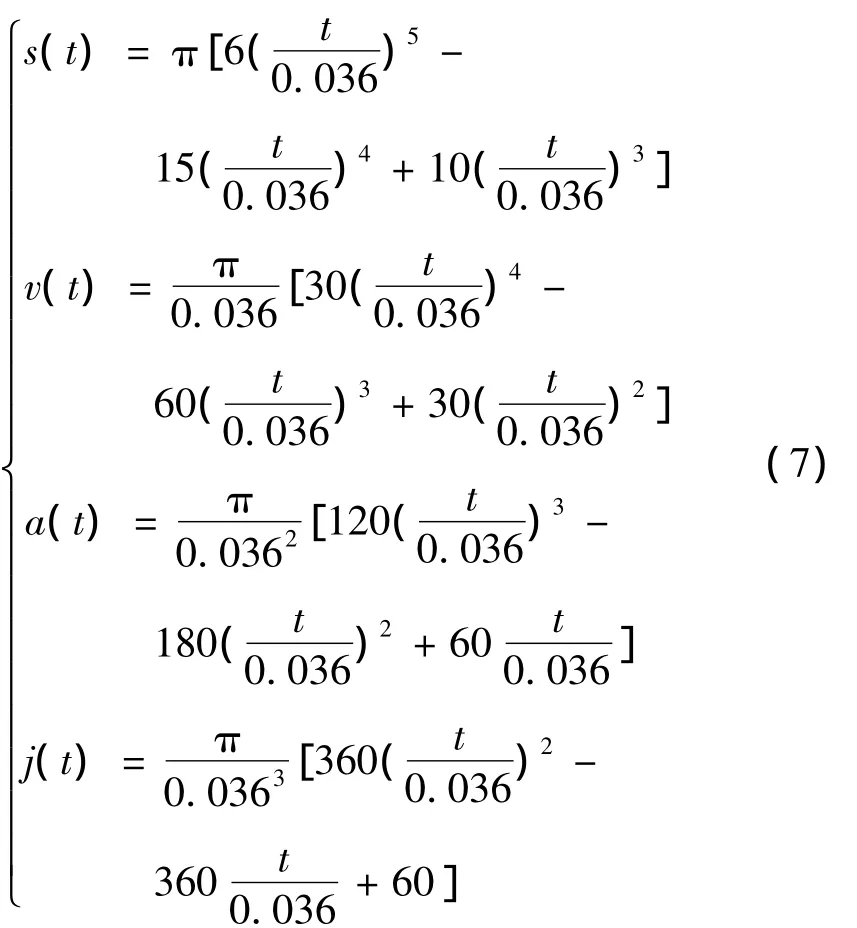
利用相关软件可以得到式(7)的曲线，如图3～图6所示。

此工况下，角位移曲线、角速度曲线、角加速度曲线及角加加速度曲线十分平滑，在运动的起始和终止阶段也没有突变点，这就可以很好地保证固晶臂运动的平滑性并有效抑制运动结束后的振动。

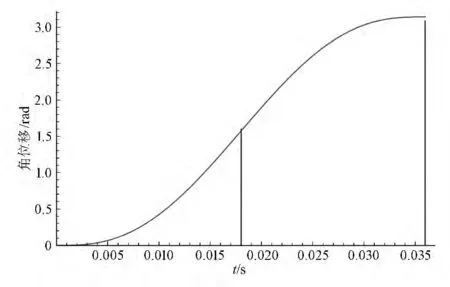
图3 五次多项式逼近的角位移曲线

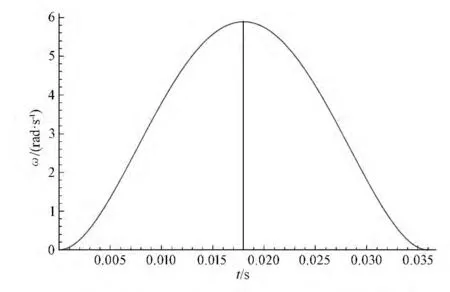
图4 五次多项式逼近的角速度曲线

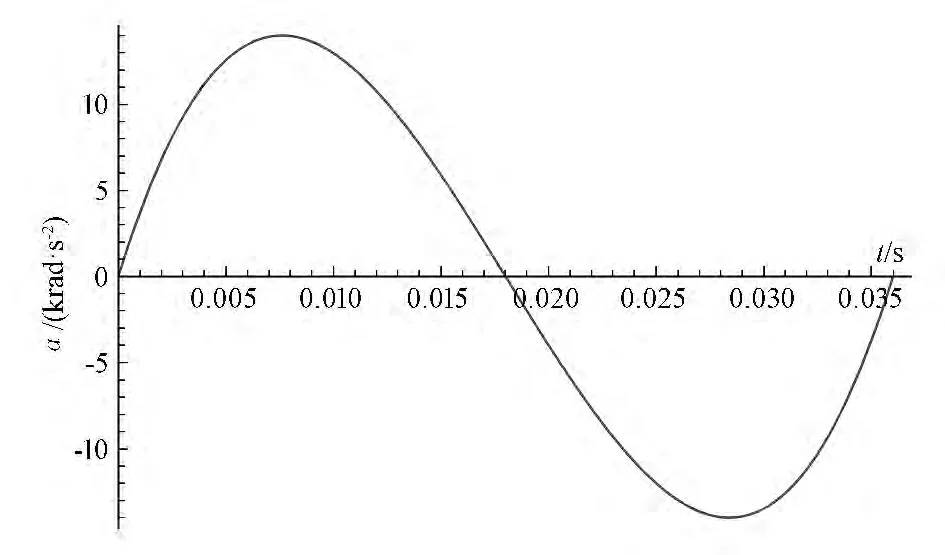
图5 五次多项式逼近的角加速度曲线

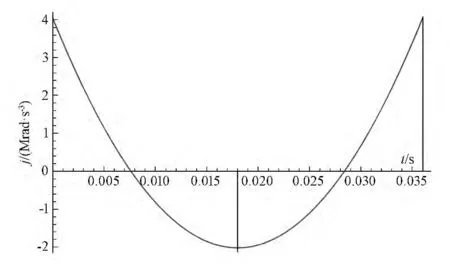
图6 五次多项式逼近的角加加速度曲线

将优化后的加减速曲线与传统梯形加减速曲线应用到固晶臂的旋转运动中去，再分析固晶臂末端的位移随时间衰减的情况。应用传统加减速曲线的固晶臂末端的位移衰减情况如图7所示，应用五次多项式拟合的加减速曲线的固晶臂末端的位移衰减情况如图8所示。

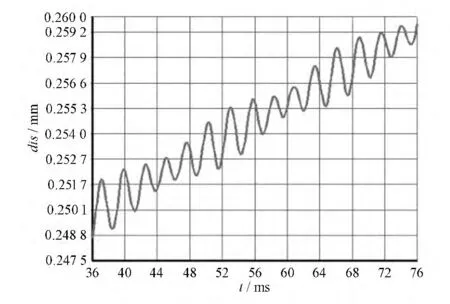
图7 应用传统加减速曲线的固晶臂末端的位移衰减

经比较发现，应用传统梯形加减速曲线的固晶臂末端振动十分剧烈，在规定时间内不能趋稳，而应用五次多项式拟合加减速曲线的固晶臂末段位移在10ms左右降为零，能够满足LED芯片键合机的工作要求。

5 结束语

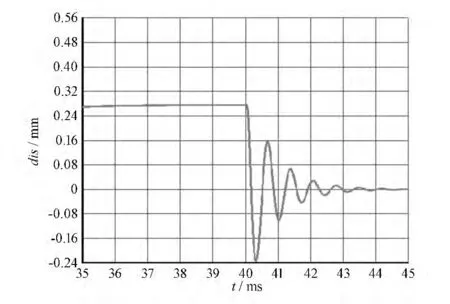
图8 应用五次多项式拟合的加减速曲线的固晶臂末端的位移衰减

本文利用多项式拟合的方法提出的新型S型加减速曲线，在弥补传统加减速运动控制曲线缺点的同时还为本行业及类似工程应用问题提出了新的解决方案，但是此多项式拟合的S型加减速曲线还需结合比较完善的闭环系统才能更好地应用于类似工程中。

［1］ 吴玲.抓住产业发展关键时期培育半导体照明战略性新兴产业［J］.新材料产业，2011(4):1－4.

［2］ 林晓新，吴小洪，曹占伦，等.S曲线加减速控制在LED芯片键合机中的应用［J］.机械制造，2008，46(5):21－23.

［3］ 郎平，郭东.COSMOS在LED芯片键合机芯片拾取臂振动分析中的应用［J］.封装与测试，2011(5):21－24.

［4］ 李丹.多项式拟合柔性加减速算法的研究［J］.制造业自动化，2010，33(3):158 －160.

［5］ 李晓辉，邬义杰，冷洪滨.S型加减速控制方法的研究［J］.组合机床与自动化加工技术，2007(10):49－53.