起落架四点布局无人机着陆动力学分析

牟 丹，聂 宏，2，张 明，2

(1.南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏南京 210016)(2.南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016)

随着无人机技术不断发展，其越来越广泛地应用于民用和军事方面。着陆阶段是无人机飞行过程中的重要阶段，同样也是安全事故频发的阶段，飞机着陆过程中，起落架和机身都会受到强烈的冲击载荷，这种冲击载荷正是引起机身和起落架结构发生破坏的重要因素［1］。因此，着陆过程中起落架和机身的动态响应一直是飞机着陆动力学分析的重要课题。

国外对起落架四点布局无人机已经有了一定的研究［2］，国内相关研究较少。目前，对三轮布局无人机地面动力学的研究主要集中在前轮摆振稳定性、滑跑稳定性和地面转弯操作等方面［3－5］。其中文献［6］、［7］进行了较为详细的研究，但作者对模型进行了简化，仿真不是以六自由度模型为基础。文献［8］虽然建立了飞机地面滑跑模型，但没有考虑起落架缓冲器运动特性。文献［9］、［10］考虑了起落架缓冲器的数学模型，但忽略了轮胎侧向特性，仅加入了轮胎纵向特性。

本文以起落架四点布局无人机为研究对象，建立了包含缓冲器模型、轮胎模型、气动力模型的六自由度飞机动力学模型，对飞机不同着陆姿态进行仿真分析，探讨了不同着陆迎角、滚转角对飞机过载及起落架和轮胎载荷的影响。

1 基本假设

本文所研究的起落架四点布局飞机是一个复杂的多自由度系统，为使所建立的模型能够精确模拟实际运动情况，又便于计算，现对模型作以下假设:

1)把飞机分成弹性支撑质量和非弹性支撑质量两部分，其中弹性支撑质量指缓冲器支撑质量，包含机翼、机身以及缓冲器外筒等部件;非弹性支撑质量是指包括机轮、起落架活塞杆以及车架等在内的质量。在机体的刚体运动方程中可以反映出弹性支撑质量运动规律，各非弹性支撑质量被视为集中质量，且具有独立的自由度。

2)弹性支撑质量运动为六自由度的刚体运动，质量集中在飞机质心;非弹性支撑质量运动只考虑3个平动方向自由度，质量集中于车架与缓冲支柱连接点或机轮质心［11］。

3)不考虑各缓冲支柱弹性变形。

4)机轮具有独立旋转自由度。

5)气动力作为集中力处理。

2 动力学模型

2.1 系统受力分析

飞机在着陆过程中受到自身重力、空气动力、发动机推力、地面支反力的作用［12］，运用牛顿第二定律和相对质心的动量矩定理，在机体坐标系中建立机体的动力学微分方程组。

平动方程:

转动方程:

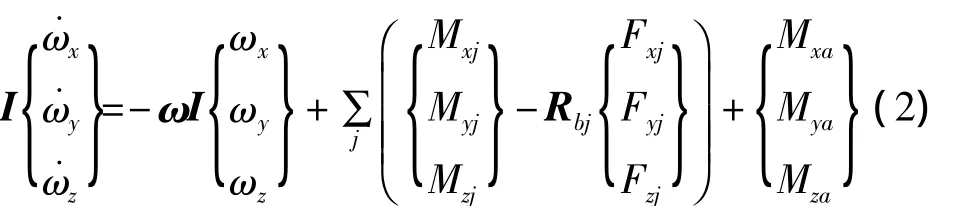
式中:mb为机体质量为机体质心速度矢量;［ωxωyωz］T为机体坐标系的旋转角速度;［0 0 Wb］T为发动机推力矢量;L］T为3个方向气动力矢量;为j起落架作用于机体的作用力矢量;为飞机角的加速度矢量;［MxjMyjMzj］T为起落架作用于机身力矩矢量;［MxaMyaMza］T为3个方向的气动力矩矢量;Rbj为各起落架轮轴到飞机质心距离矩阵;I表示机身的转动惯量矩阵;ω为机身角速度矩阵。

2.2 相关力学模型

2.2.1 起落架缓冲器轴向力模型

起落架的缓冲器轴向力fs主要由3部分构成，分别为油液阻尼力fh、空气弹簧力fa和摩擦力ff。在缓冲器处于全伸长状态或者缓冲器压缩到最大行程状态时，fs由缓冲器的结构限制力来确定。fs统一表示为:

式中:Ks为缓冲器的结构限制刚度;Smax为缓冲器的最大压缩行程;S0为缓冲器全伸长时的行程。

空气弹簧力:

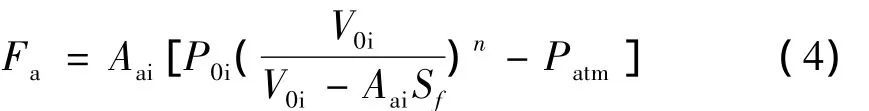
式中:P0i为缓冲器的初始填充压强;Aai为压气面积;V0i为缓冲器的初始充气容积;n为气体的多变指数;Patm为当地大气压强;Sf为缓冲器压缩行程。

油液阻尼力:

式中:ρoil为油液密度;Adi为主油腔的油孔面积;Ahi为缓冲器的有效压油面积;Cdi为主油腔油孔的缩流系数;Ani为回油腔的油孔面积;Ahsi为缓冲器回油腔的有效压油面积;Cdsi为回油腔油的孔缩流系数。

缓冲器内部的摩擦力由两部分所组成，即皮碗摩擦力和由于缓冲支柱弯曲而在上下支撑点产生的库仑摩擦力:

式中:Nu，Nl分别是缓冲支柱的上下支撑点处所产生的正压力;μb为库仑摩擦系数。

2.2.2 轮胎力模型

本文采用521轮胎模型，如图1所示，该模型考虑了轮胎的纵向滑移、侧倾以及侧滑。轮胎所受到的地面载荷为垂向支反力、航向摩擦力和侧向摩擦力。

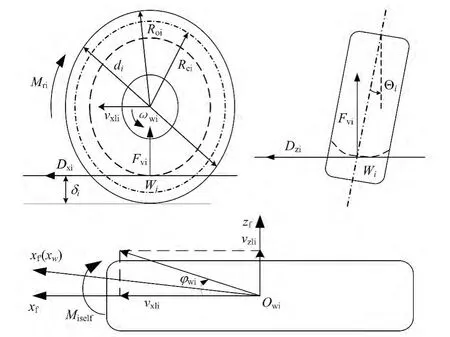
图1 轮胎力学特性

垂向支反力:

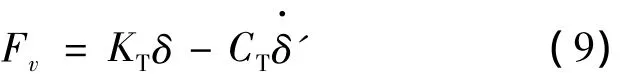
式中:CT为轮胎垂直振动阻尼系数;KT为轮胎垂直振动刚度分别为轮胎压缩量和压缩速度。

航向摩擦力:

式中:μt为轮胎航向粘着系数，与轮胎航向滑移率有关。模型采用以下经验公式:

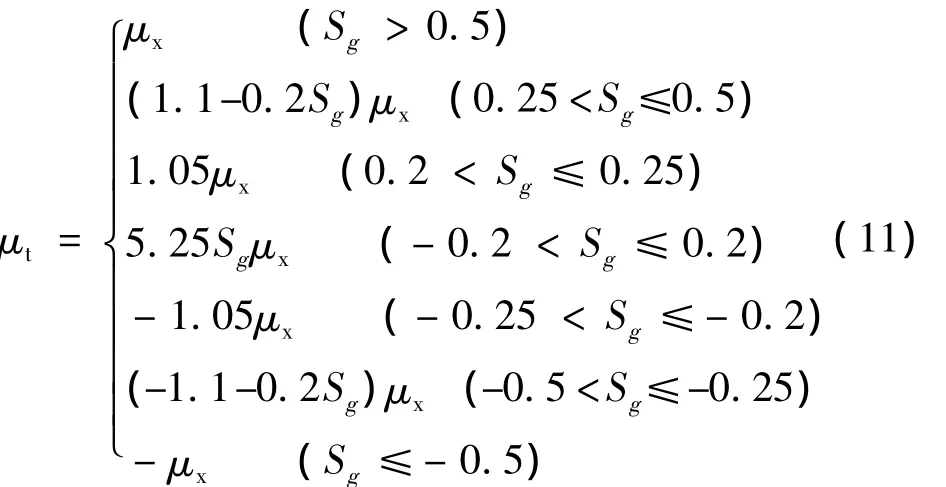
式中:μx为航向静摩擦系数;滑移率Sg=(VxωRe)/Vx，其中Re为轮胎转动半径。

侧向摩擦力:

其中:

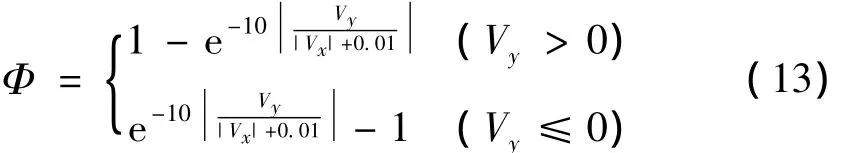
式中:μa为轮胎偏航系数;Vy，Vx分别为轮胎速度。

2.2.3 气动力模型

气动力在气流坐标系中表述，由3个方向的分量组成:沿ya正向的升力Y、沿xa轴负向的阻力Q以及沿 za轴的侧力 Z。气动力矢量表示为［-Q Y Z］T。其中:

滚转力矩、偏航力矩、俯仰力矩分别为:

式中:ρ为当前高度大气密度;u为当前飞机的速度;Sref为机翼参考面积;Cmx，Cmy，Cmz分别为滚转、偏航、俯仰力矩系数;CD，CL，Cβ分别为阻力系数、升力系数和侧力系数。

3 仿真分析

根据2中的力学模型，在MATLAB/SIMULINK中建立包含缓冲器模型、轮胎模型、气动力模型的六自由度飞机动力学模型，对飞机不同着陆姿态进行仿真分析，给定无人机水平着陆速度50m/s，下沉速度2m/s，发动机推力100kg，在着陆瞬间认为升力大小与飞机质量相同。

3.1 不同着陆俯仰角仿真分析

对飞机 0°、4°、6°和 8°俯仰角着陆状态进行仿真，图1给出了着陆过程中飞机主起轮胎载荷－时间曲线、飞机质心加速度－时间曲线、主起功量图。

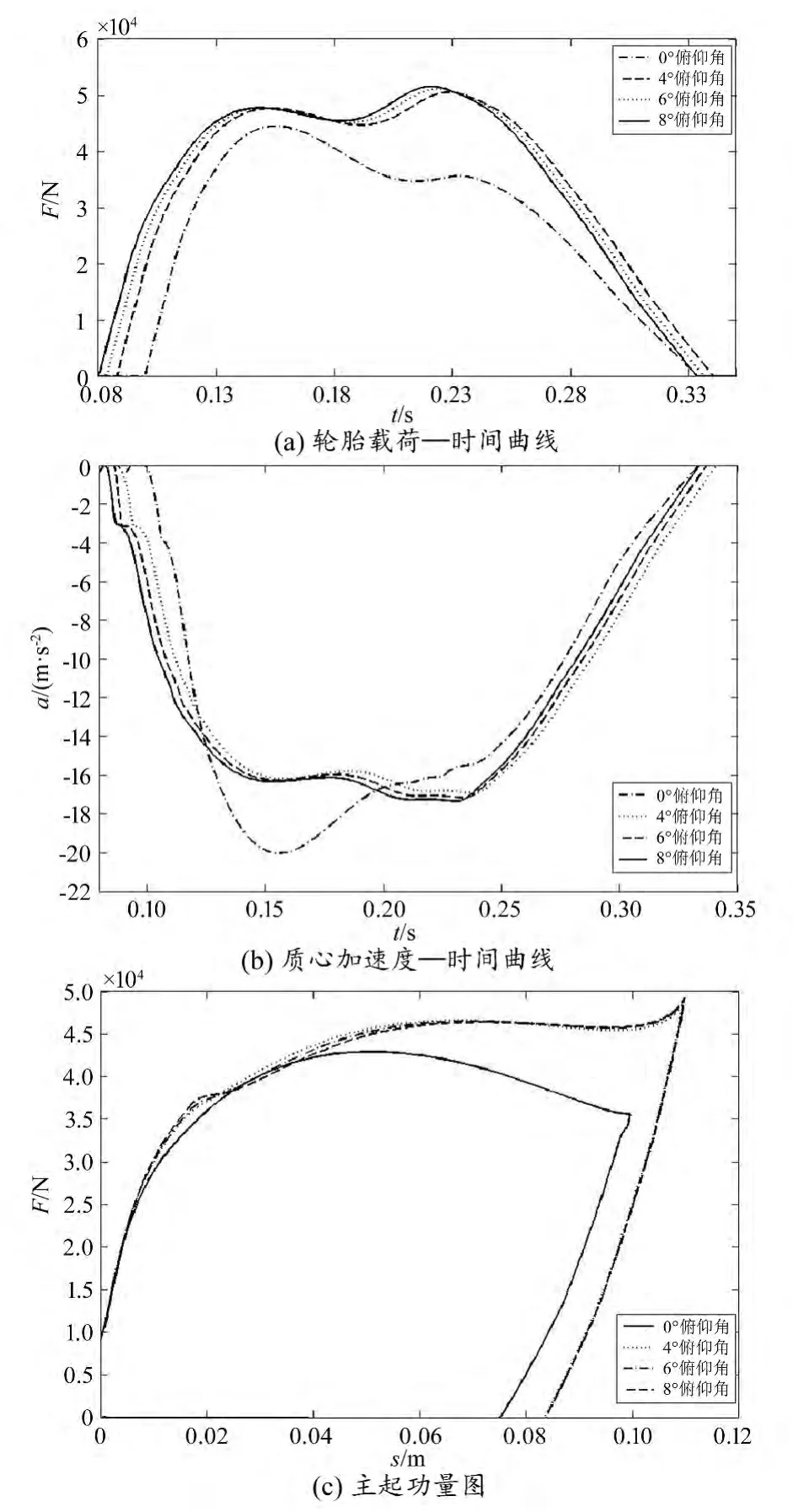
图2 不同俯仰角仿真结果

由图2(a)可以看出，相对于水平着陆，俯仰角为正时主起轮胎载荷明显增大，且载荷最大值出现时间后移，随着陆俯仰角增大主起轮胎载荷增加，但增量较小;由图2(b)可知，相对于水平着陆，俯仰角为正时飞机质心加速度减小，且峰值出现时间后移，随俯仰角增大质心加速度增大;图2(c)显示，相对于水平着陆，俯仰角为正时主起吸收能量显著增加，随着陆俯仰角增大主起吸收能量增加，但增量较小。表1给出了不同俯仰角着陆情况下轮胎最大载荷以及质心的最大过载。

表1 不同俯仰角仿真结果对比

3.2 不同着陆滚转角仿真分析

对飞机2°、4°滚转角着陆状态进行仿真，图2给出了着陆过程中飞机轮胎载荷－时间曲线、前起功量图、主起功量图。

由图3(a)可以看出，先接地一侧的轮胎载荷明显大于后接地一侧的轮胎载荷，且先接地一侧轮胎载荷随滚转角增加而缓慢增加，后接地一侧轮胎载荷随滚转角增加而显著减小，主起轮胎和前起轮胎都遵循以上规律;由图3(b)、图3(c)可知，存在着陆滚转角的情况下，先接地一侧的起落架吸收能量较多，且随滚转角增加吸收的能量显著增加;随着滚转角增大，后接地一侧起落架吸收能量减小，其中前起吸收能量的减小量多于主起。这表明相对于三点布局飞机，起落架四点布局飞机在存在滚转角着陆时前起可以吸收部分能量，有效减小主起着陆过程中的冲击载荷。表2给出了不同滚转角角着陆情况下轮胎最大载荷。

表2 不同滚转角轮胎最大载荷仿真结果对比

4 结论

本文以起落架四点布局无人机为研究对象，建立包含缓冲器模型、轮胎模型、气动力模型的六自由度飞机动力学模型，对无人机不同俯仰角、滚转角着陆进行动力学仿真分析，得到以下结论:

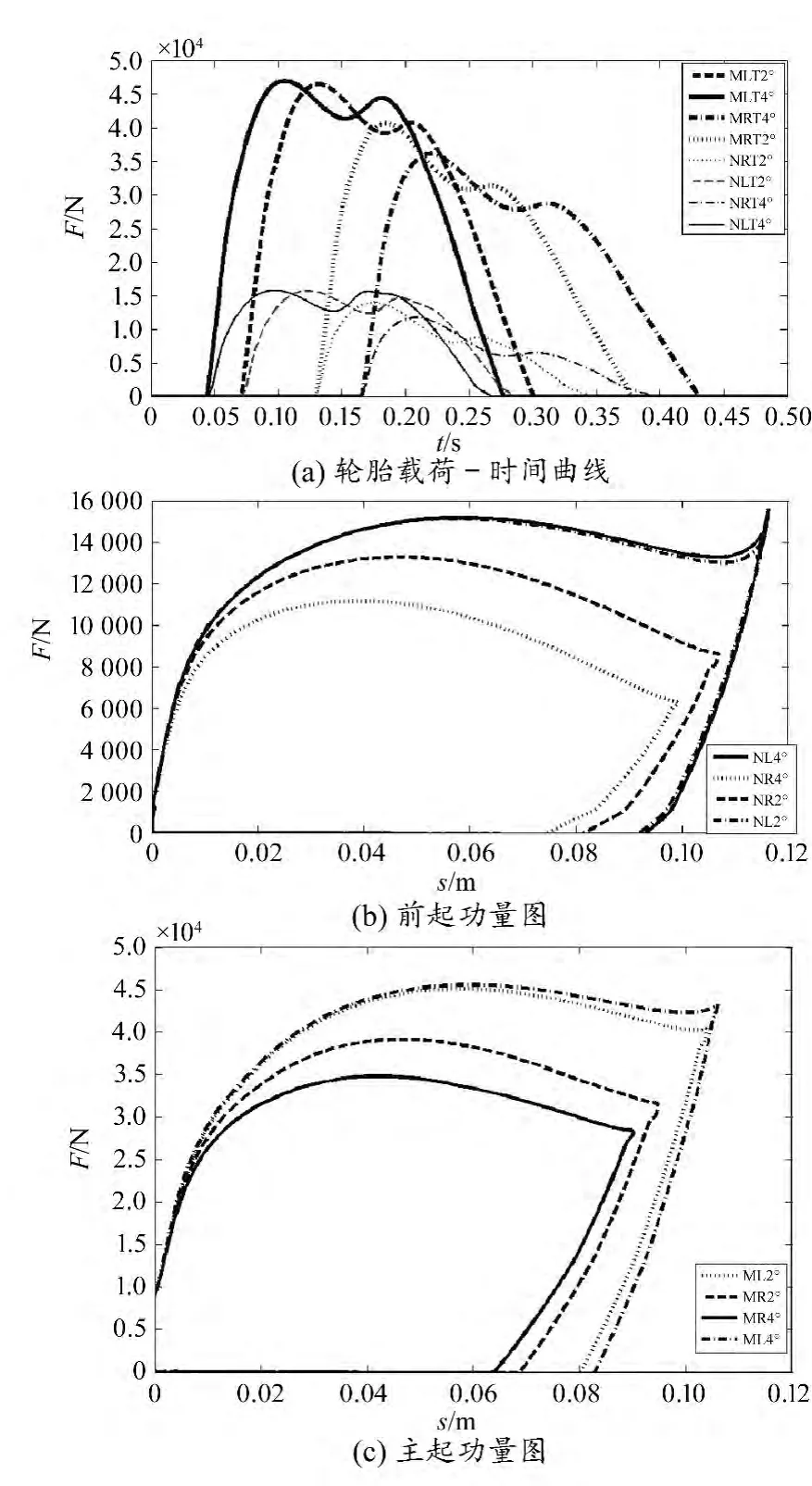
图3 不同滚转角仿真结果

1)飞机不同俯仰角着陆的仿真分析表明，相对于水平着陆，俯仰角为正时主起轮胎载荷明显增大，飞机质心加速度减小。随着陆俯仰角增大主起轮胎载荷和飞机质心加速度增加，但增量较小。

2)飞机不同滚转角着陆的仿真分析表明，存在滚转角着陆时，起落架四点布局飞机先接地一侧前起能够吸收部分能量，有效减小主起落架着陆过程中的冲击载荷;随滚转角增加先接地一侧轮胎载荷缓慢增加，后接地一侧轮胎载荷显著减小;且随着滚转角增大，后接地一侧起落架吸收能量减小，其中前起吸收能量的减小量多于主起。

［1］ Choi Y T，Wereley N M.Vibration control of a landing gear system featuring electrorheological/magnetorheological fluids［J］.Journal of Aircraft，2003(40):432 －439.

［2］ Janetka，Filz M，Smith Letal.Unmanned Air－ Ground Vehicle［R］.AIAA 2011－3433.2001.

［3］ 顾宏斌.飞机地面运行的动力学模型［J］.航空学报，2001，22(2):163－167.

［4］ 王孝英，诸德培.飞机操纵前轮转弯运动的数学模型及数值仿真［J］.应用力学学报，1997，14(4):46－50.

［5］ 杨新，王小虎，申功璋，等.飞机六自由度模型及仿真研究［J］.系统仿真学报，2000，12(3):210－213.

［6］ 李峰，曹云峰，曹美文.某型无人机着陆过程中地面滑行段的建模与仿真［J］.指挥控制与仿真，2006，28(2):91－94.

［7］ 段云松，朱纪洪，孙增圻.无人机着陆数学模型研究——三轮着地滑行［J］.系统仿真学报，2004(6):1296－1299.

［8］ Sivaramakrishnan M M.Influence of landing gear flexibility on aircraft performance during ground roll［J］.Journal of Aircraft，1981(2):991－992.

［9］ Horta L G，Daugherty R H，Martinson V J.Modeling and validation of a navy A6－intruder actively controlled landing gear system［R］.NASA/TP－1999－20124，1998.

［10］袁东.飞机起落架仿真数学模型建立方法［J］.飞行力学，2002，20(6):44 －47.

［11］张明.飞机地面动力学若干杆件技术研究［D］.南京:南京航空航天大学，2009.

［12］段萍萍.舰载飞机着舰过程动力学性能分析［D］.南京:南京航空航天大学，2011.