RV减速器几何回差分析与系统参数优化设计

张 诚，张建润

(东南大学机械工程学院，江苏南京 211189)

RV减速器相对于一般减速器而言质量轻、体积小、寿命长，并且传动比范围大、回差小、传动精度高。工业机器人的发展趋势是向高速、高精、重载、轻量化和智能化方向发展［1］，RV减速器多用于工业用机器人，在近年来受到越来越多的国内外专家的重视，RV传动技术的发展也越来越迅速。因此，RV传动技术的研究具有实际意义。

1 RV减速器的结构及研究现状

RV传动是一种新型的、二级封闭式、少齿差行星传动机构。RV减速器由渐开线行星齿轮传动和摆线针轮行星传动两部分组成。RV减速器的几何结构如图1所示。文献［2］中给出了RV减速器的工作原理。

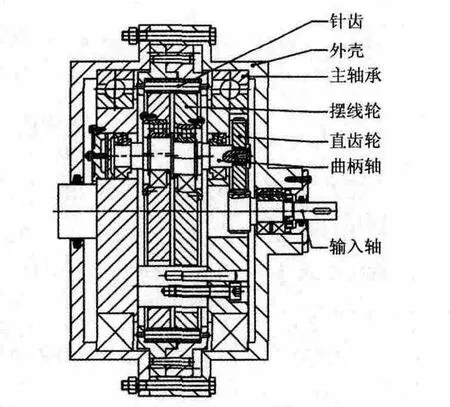
图1 RV减速器几何结构图

国内外有很多研究者致力于RV传动技术的研究。在国内，有学者提出对比渐开线少齿差行星传动减速器和摆线针轮行星传动减速器各项特性，使用效果等效原则，以摆线齿轮的齿高平均圆直径和当量模数为线索查取渐开线齿轮公差，从而获得摆线齿轮公差［3］。在国外，早在20世纪90年代，Blanche J.G.和 Yang D.C.H.已经对摆线传动的公差进行了研究［4－5］。但是，这些研究都忽略了回差对RV减速器的影响，因此他们所提出的方法存在不足。而21世纪以来，研究者都偏向于对RV减速器结构的改进，文献［6］提出了一种新型摆线轮减速器结构，文献［7］提出了用摆线内啮合齿轮代替针轮能够有更好性能的观点，并建立模型进行分析。但是，他们对于减速器的回差计算以及系统参数的研究不多。

回差是衡量RV减速器工作性能的主要参数之一，回差对反馈控制系统具有直接的影响，同时还影响到系统的动态品质［8］。因此，控制回差满足减速器传动精度要求对于减速器的设计十分重要。根据对减速器的几何回差进行计算，可以验证所确定的系统参数是否合适，当验证结果为不合适时，可以根据几何回差修改参数误差。由于几何回差是减速器性能的重要组成部分，所以利用几何回差确定参数误差具有合理性。

2 RV减速器的几何回差分析

根据RV减速器的结构及工作原理，其传动引进的几何回差可以分为两部分:第一部分为渐开线行星传动引起的回差，第二部分为摆线针轮行星传动部分引起的回差。

由于本文利用回差计算进行参数优化，因此将以综合回差的上限值为限定值，进行系统参数的优化设计。

2.1 渐开线圆柱齿轮传动的几何回差

影响渐开线圆柱齿轮传动的几何回差的因素主要为齿轮啮合的固有侧隙和装置误差。齿轮啮合的固有侧隙主要由最小侧隙和侧隙公差决定;装置误差主要包括中心距误差及有关零件的配合间隙与制造误差等。计算时主要考虑公法线长度平均偏差引起的齿轮侧隙、中心距误差以及齿轮齿圈径向误差引起的回差［9］。

渐开线齿轮传动部分产生的回差Δφ12求解公式为:

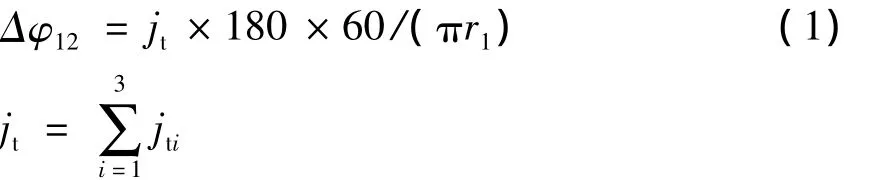
式中:r1为太阳轮分度圆半径;jt为齿轮传动侧隙，其中jt1为公法线长度平均偏差(Ews，Ewi)引起的侧隙，jt2为中心距误差ΔFe引起的侧隙，jt3为齿圈径向跳动误差ΔFr1引起的侧隙。本文主要考虑公法线长度平均偏差引起的测隙，即jt1。因此，渐开线齿轮传动部分产生的回差Δφ12可转化为:

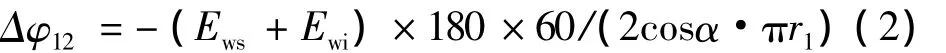
2.2 摆线针轮行星传动的几何回差

摆线针轮行星传动部分产生的回差Δφ34的求解公式为:

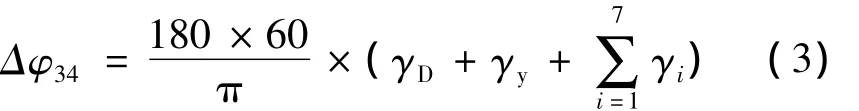
式中各参数含义及计算过程详见文献［9］中17－132～17－133，本文不作具体阐述。

将各个参数的计算公式代入式(3)，得到摆线针轮行星传动部分产生的回差Δφ34为:

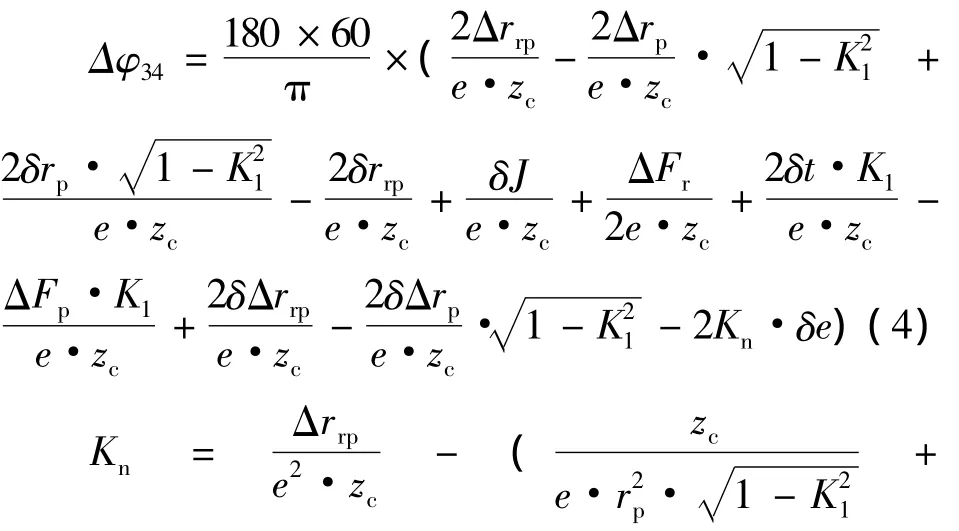
式中:Δrrp为等距修形量;Δrp为移距修形量;δrp为针齿中心圆半径偏差;δrrp为针齿销半径误差;δJ为针齿销与针齿销孔的配合间隙;ΔFr为摆线轮齿圈径向圆跳动误差;δt为针齿销孔圆周位置度误差;ΔFp为摆线轮周节累计误差;δΔrrp为等距修形误差;δΔrp为移距修形误差;δe为偏心距误差;K1为短幅系数;e为摆线轮偏心距;zc为摆线轮齿数;rp为针轮半径。

2.3 轴承间隙对几何回差的影响

RV减速器的转臂轴承存在一定的游隙，所以会产生相应的回差。该回差的计算公式为:

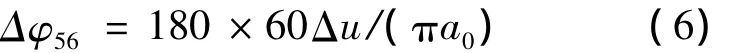
式中:Δu为转臂轴承的游隙;a0为行星轮与太阳轮的中心距。

2.4 减速器整体几何回差

减速器的整体几何回差公式为:

将各个参数代入式(7)，得到计算减速器整体几何回差的公式:

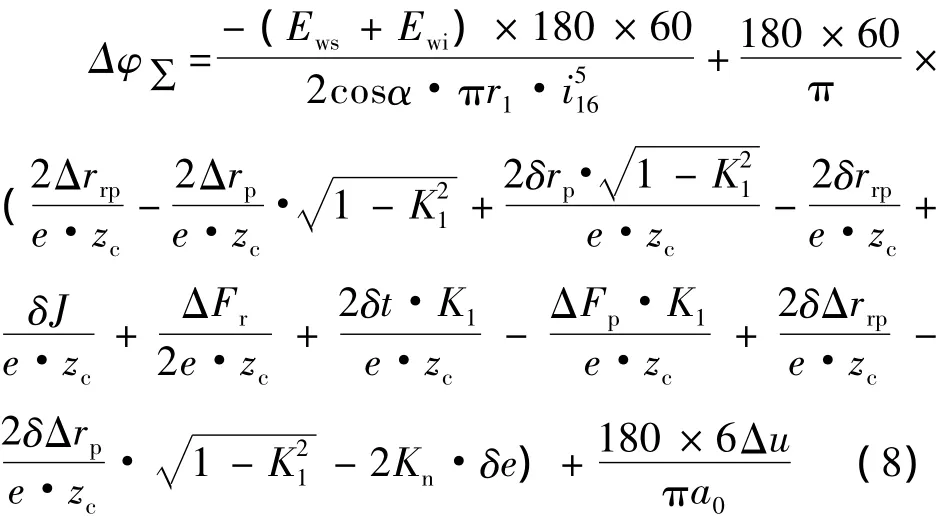
由文献［9］可知，RV减速器的几何回差一般小于1'，因此目标函数为Δφ∑ ≤1'，约束条件为零件加工的成本，表现为各参数的取值带来的零件加工的难易程度。

根据式(8)计算回差时需要用到的参数见表1，即可以通过计算回差，确定表中参数。

式(8)得到的减速器的几何回差是表1中各个参数产生的回差分量的总和。由于各个回差分量之间相互独立，所以当且仅当各个回差分量的最大值之和小于要求值时，才符合条件。因此，根据回差计算，可以得到系统参数的上限值。

表1 回差分量对应的参数误差

3 几何回差的灵敏度分析及参数优化

根据表1可以发现，渐开线圆柱齿轮公法线长度上、下偏差，摆线针轮等距修形量、移距修形量等参数决定了减速器几何回差的大小。因此，当已知所要设计的RV减速器的几何回差要求时，可以用于检验并且修改这些系统参数的数值。

参数优化的具体方法如图2所示。

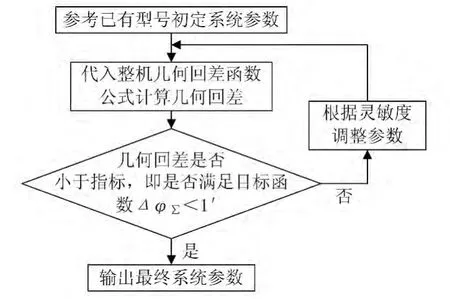
图2 参数优化流程图

图2 中，初定所设计型号的系统参数时，以已有RV减速器各个零件加工等级作为参考，尽量选取较大数值，以便于加工。

优化参数的难点在于如何修改参数，使得计算得到的回差符合要求。一般情况下，初定系统参数时所选取的参数与所要求的回差会有一定差距，这就需要设计者对初定的参数进行修改。通过对式(8)进行灵敏度分析，即可找出表1中对几何回差影响较为重要的几个参数。

设有函数 Y(X1，X2，…，Xn)，若各个参数 Xi存在误差 ΔXi，则对函数 Y(X1+ ΔX1，X2+ ΔX2，…，Xn+ΔXn)进行一级泰勒展开得:

对于回差函数式(8)，可根据灵敏度分析，求出各个参数的相对灵敏度(见表2)，其中S0取值为等距修形量Δrrp的灵敏度。

表2 系统参数的相对灵敏度

根据表2可知，不同的RV减速器，因为具有不同的短幅系数K1、偏心距e、摆线轮齿数zc等参数，所以表中的各个系统参数的相对灵敏度是有区别的。当分析某个具体实例时，只需将具体参数代入表2比较大小即可找出对几何回差结果影响较大的参数。然后，根据计算结果与要求回差的大小，确定增加或者减小的参数对象(即相对灵敏度最大的几个系统参数)以及改变的数值。在优化参数的过程中，应遵循有利于加工的原则，即优先增大较小值，减小较大值。

4 设计实例

某款RV减速器的基本参数:输入功率P为2.5kW，输入转速n为2 000r/min，传动比 i为78，短幅系数K为0.73，偏心距e为2mm，行星轮与太阳轮中心距a0为51mm，摆线轮齿数为41，针齿数为42，针轮半径rp为115mm，太阳轮齿数为18，行星轮齿数为33，模数均为2mm。设计回差要求为几何回差 Δφ∑ ≤1'。

根据上述减速器尺寸，在加工要求等级内尽量取上限，系统参数初取值见表3。

表3 实例中系统参数初取值

将表3中的系统参数初取值代入式(8)，计算得 Δφ∑ =1.302'。已知要求几何回差Δφ∑≤1'，所以要减小参数数值，以满足回差要求。

将已知参数代入表2得到表4。

表4 实例中系统参数的灵敏度

从表4可知对几何回差影响较大的几个系统参数为:等距修形量Δrrp、针齿销半径误差δrrp、等距修形误差δΔrrp、曲柄轴承的游隙Δu、针齿销孔圆周位置度误差δt。

考虑到摆线轮修型工艺较为复杂，所以不宜减小等距修型量及误差，而针齿销半径误差相对灵敏度为负值，即减小时回差反而增大。因此，对其他两个系统参数做迭代优化，即根据初始回差结果，先随意选取两参数的调整量代入式(8)，根据回差结果确定调整量的大小，并划分步长，从初始值按小步长依次调整两个参数，然后代入式(8)，直至满足目标函数。最终优化值如下:针齿销孔圆周位置度误差 δt=0.014mm，曲柄轴承的游隙 Δu=0.007mm。

由此可得优化参数后的总几何回差Δφ∑ =0.977'，满足要求。

本例中所优化的系统参数是加工时尺寸的上限，只要满足实际加工值小于此系统参数，几何回差就满足要求。

5 结论

1)几何回差在影响减速器性能的因素中具有重要地位，本文首次提出将几何回差上限值作为优化RV减速器系统参数的约束，具有合理性。

2)优化参数时，对所建立的模型进行灵敏度分析，有利于区分各个参数对于几何回差的重要性，从而确定优化对象。

3)在符合理论要求的情况下，应该考虑所设计参数对应的加工难易程度，从简化加工要求的角度出发优化参数。

4)本文所述的方法不仅可以用于RV减速器系统参数的确定，对于其他类似结构也有参考作用。

［1］ 骆敏舟，方健，赵江海.工业机器人的技术发展及其应用［J］.机械制造与自动化，2015(1):1－4.

［2］ 何卫东，刘珂荧，吴鑫辉.机器人用RV减速器参数化设计［J］.大连交通大学学报，2015(1):47 －50.

［3］ 姚文席.摆线齿轮公差的一种选取方法［J］.工具技术，2003(6):45－48.

［4］ Blanche J G，Yang D CH.Cycloid drives with machining tolerances［J］.Journal of Mechanical Design，1989，111(3):337 －344.

［5］ Yang D CH，Blanche JG.Design and application guidelines for cycloid drives with machining tolerances［J］.Mechanism and Machine Theory，1990，25(5):487 －501.

［6］ Blagojevic M，Marjanovic N，Djordjevic Z，et al.A new design of a two － stage cycloidal speed reducer［J］.Journal of Mechanical Design，2011，133(8):1－7.

［7］ Hsieh C F.Dynamics analysis of cycloidal speed Reducers with pinwheel and nonpinwheel designs［J］.Journal of Mechanical Design，2014，136(9):1－11.

［8］ 吴永宽，郑剑云，陈天旗，等.摆线针轮行星传动的几何回差分析计算［J］.大连铁道学院学报，1999(2):28 －32.

［9］ 机械设计手册编委会.机械设计手册:上册［M］.新版.北京:机械工业出版社，2004.