某型飞机纵向运动MATLAB建模及仿真研究

2015-05-07杨志丹

机械设计与制造工程 2015年8期

杨志丹

(上海飞机设计研究院飞控部，上海 200120)

自从飞机问世以来，飞行安全一直是飞机设计的最高目标，飞机的各项设计目标都要服从这项最高目标。一个良好的飞行控制系统应能在保证飞机飞行安全前提下更好地完成飞行目标。现代飞机所需满足的飞机功能和飞行控制需求越来越复杂，导致飞行控制系统的控制率越来越复杂。传统的理论计算难以满足新技术的发展，在现代飞行控制系统设计过程中，MATLAB仿真软件被大量应用于飞行控制系统的建模仿真。利用MATLAB仿真软件对飞行控制系统的各个方面进行建模仿真分析不仅能够节约更多的时间和精力，而且仿真分析结果相比于以前的纯理论计算结果更接近实际情况。

1 飞机的气动力和力矩分析

飞机在空中飞行时，其表面分布着空气动力，这些力可以归结为一个作用于飞机质心的合力R∑(总空气动力)和一个绕其质心的合力矩M∑(总空气动力矩)。作用在飞机上的力和力矩决定着飞行器的运动，要控制飞机的运动就必须改变这些力和力矩并使它们按照要求的规律改变［1］。飞机坐标系如图1所示，本文着重对飞机纵向运动(绕机体坐标系y轴的运动)的力和力矩进行研究。

1)升力L，即R∑ 沿气流坐标系Za轴的分量，向上为正。产生升力的主要部件是飞机的机翼。

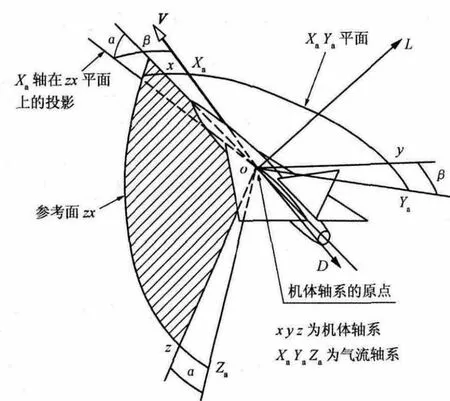
图1 飞机坐标系

2)阻力D，即R∑沿气流坐标系Xa轴的分量，向后为正。

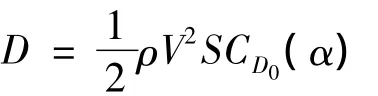
3)纵向力矩M(俯仰力矩)，是指作用于飞机的外力所产生的绕机体坐标系y轴的力矩，包括气动力矩和发动机推力向量因不通过飞机质心而产生的力矩。

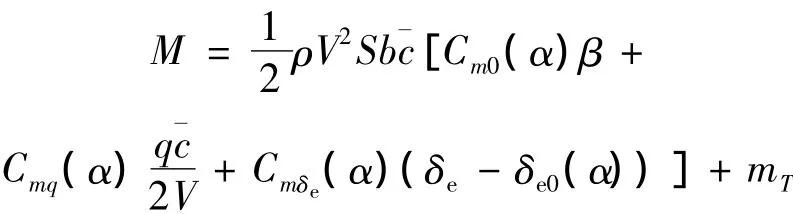
式中:α，β，V，S，¯c和 b 分别表示迎角，侧滑角，速度，机翼面积，平均空气动力弦和翼展;ρ为空气密度;mT为发动机推力产生的俯仰力矩;Ci(α)(i=L0，Lδe，m0，mq，mδe，D0，……)为气动系数，是迎角的函数，其详细定义参见文献［1］。

Tx，Ty和Tz分别表示发动机的推力T在喷口产生的沿机体坐标系3个轴方向的推力分量。

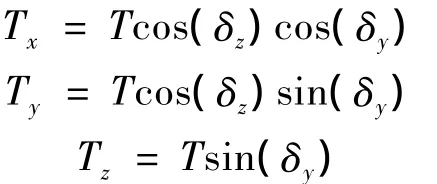
式中:δy，δz是推力矢量舵侧向和纵向的偏转角。发动机推力T可产生俯仰力矩mT和偏航力矩nT。

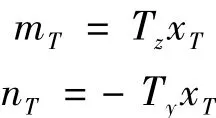
式中:xT为发动机喷口与飞机质心之间的距离。

2 非线性数学模型的建立及线性化分析

系统数学模型一般都是线性的，但在实际问题中纯粹的线性模型并不多见，大多数系统都是非线性的或者在特定条件下呈现线性特征［2］。飞机飞行状态的描述十分复杂，尤其在做机动飞行任务时，整个系统为一个时变的、非线性、强耦合系统，其数学模型难以确定。为此，笔者首先对飞机纵向运动构建其非线性数学模型:

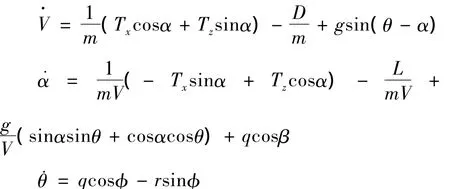
式中:α，β，φ，θ分别是迎角、侧滑角、偏航角、俯仰角;p，q，r分别为角速度在机体坐标系的分量(滚转角速度、俯仰角速度、偏航角速度);V，m，g分别为飞机速度、质量、重力加速度;L，D，M分别为飞机升力、阻力、俯仰力矩;Izz，Ixx，Izx，Ixy，Iyz，Iyy为飞机绕机体轴的转动惯量和惯性积。

以上非线性数学模型方程可以通过计算机数字积分法求解，但是不利于分析飞机的构型参数与飞机运动的稳定性、操纵性等问题的内在联系。为了既简化方程又不失去构型参数起主导作用的影响，可借助小扰动法对非线性方程作线性化处理，使其能用解析法求解。这样既能揭示飞机构型参数与飞行稳定性和操作性问题的内在联系，也便于知晓飞行控制系统如何控制飞机最有效。

将飞机的飞行运动分为基准运动和扰动运动，研究的关键是飞机扰动运动能否回到基准运动。小扰动法线性化可以这样理解，假设飞机扰动运动尽可能小地偏离基准运动，那么可以将非线性方程中含有扰动运动参数与基准运动参数间差值的高于一阶的小量即所谓高阶小项省略，将非线性方程变成线性方程。

用小扰动线性化方法处理纵向方程，可得如下线性数学模型:

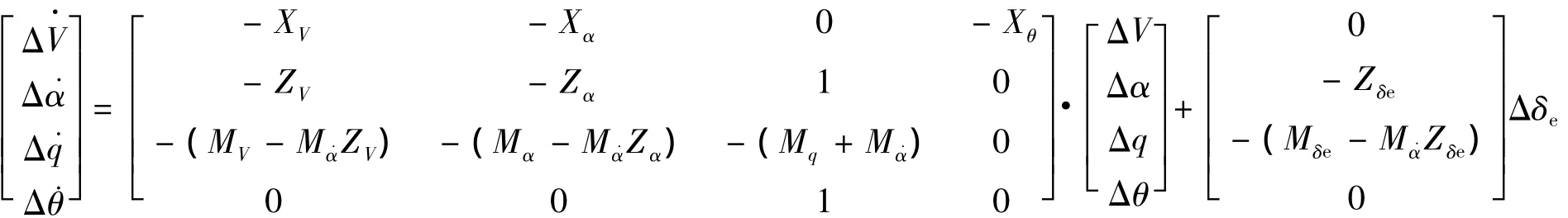
式中:XV，Xα，Xθ，ZV，Zα，Zδe，MV，M˙α，Mα，Mq，Mδe称为大导数，其详细定义参见文献［1］。

3 基于MATLAB S－function实现纵向数学模型及控制器设计

根据上述建模过程，代入相关数据可得某型飞机的纵向运动数学模型如下［3－4］:

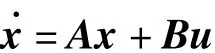
其中:

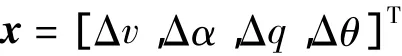
利用S函数建立飞机纵向运动线性模型:

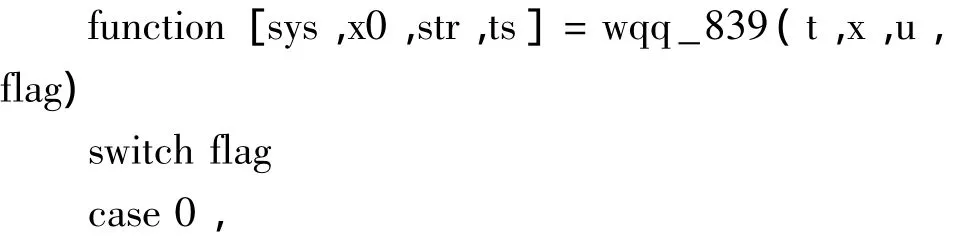
针对上述数学模型，基于比例积分微分(proportion integral derivative，PID)控制方法为其俯仰通道设计控制器，其控制结构简图如图2所示。

图2 控制结构简图

仿真中，期望的俯仰角信号选取为30°，PID控制器参数设计:比例系数为5，积分系数为1.5，微分系数为0.15。俯仰角跟踪曲线的仿真结果如图3所示。

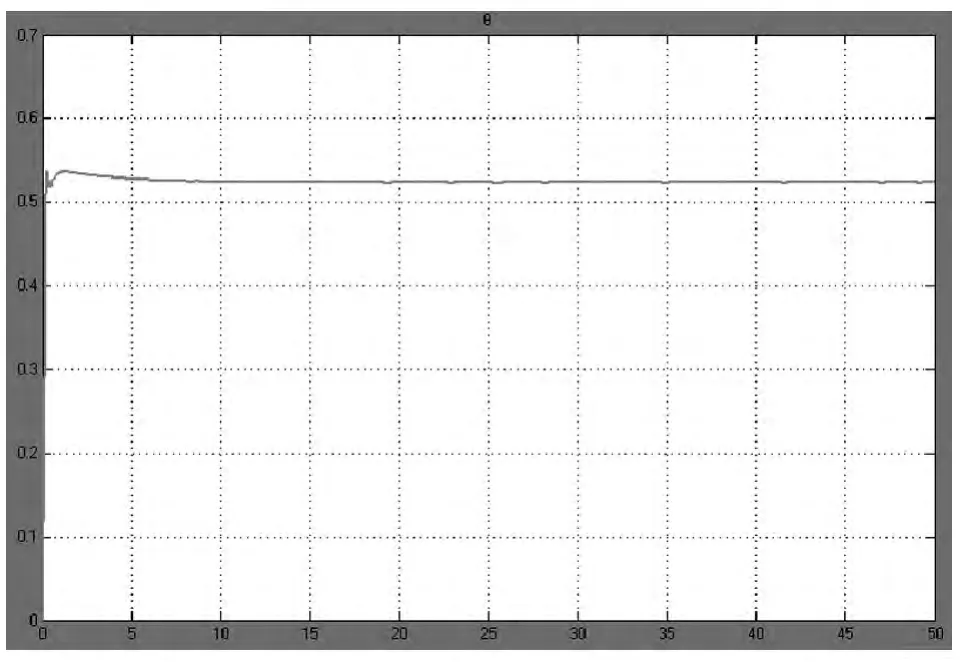
图3 俯仰角跟踪曲线

仿真结果表明:比例系数在5左右时，系统过渡过程和稳态误差处于最佳，比例系数越小，过渡过程越平缓、稳态误差越大，反之过渡过程振荡越激烈、稳态误差越小;积分系数在 1.5左右时，系统过渡过程和稳态误差处于最佳，积分系数越大，过渡过程越平缓、消除稳态误差越慢，反之过渡过程振荡越激烈、消除稳态误差越快;微分系数在0.15左右时，系统过渡过程和稳态误差处于最佳，微分系数越大，过渡过程趋于稳定、最大偏差越小，但微分系数过大，会增加过渡过程的波动程度。