均布扭矩作用下工字钢梁的应力计算

张鹭超

(现代建筑设计集团-上海建筑设计院研究院有限公司 福建厦门 361009)

均布扭矩作用下工字钢梁的应力计算

张鹭超

(现代建筑设计集团-上海建筑设计院研究院有限公司 福建厦门 361009)

论述工字钢梁扭转计算参数的基本原理，并给出了几何参数的计算方法，作为对即将出版的《钢结构设计规范》GB 50017—201X的一种补充，以便工程设计人员进行计算。特别指出：绝大多数工程设计人员在计算开口截面扭转时，均按自由扭转计算，然而即便在允许自由翘曲的支座条件下，工字梁的扭转应力也是属于约束扭转计算的一种。

扇性面积；双力矩；翘曲；自由扭转；约束扭转；应力计算

E-mail:seu040590@163.com

1 概要

在即将出版的《钢结构设计规范》GB 50017—201X中即文献[1]，提出了受扭构件的强度计算公式：

1.1 受纯扭的实腹构件，其抗弯强度可按下式计算：

(1)

式中B——构件截面的双力矩； ωn——为主扇性坐标； Iω——扇性惯性矩。

1.2 受纯扭的实腹构件，其抗剪强度可按下式计算：

(2)

式中Tω——构件截面的约束扭转力矩； Tst——构件截面的自由扭转力矩；开口薄壁截面，不考虑这一项；

Sω——扇性静矩；

t——腹板厚度；

A0——闭口截面中线所围的面积。

然而在传统的钢结构及力学相关课程中并没有详尽的介绍杆件在扭转下的应力计算。许多工程设计人员只懂得文献[3]中关于自由扭转时杆件的应力计算方法。再加上文献[2]、文献[3]对开口截面均提及自由扭转的计算方法，导致大部分工程技术人员认为开口截面杆件可以按自由扭转计算应力。这是不正确的。开口截面的自由扭转只是其扭转计算的一部分而已，只是一种理论计算，实际上开口截面的自由扭矩并不等于截面的总扭矩。

因此可以认为实际上绝大多数杆件为约束扭转(首先不是闭合的等直径圆杆)。因此出现了以自由扭转下的杆件应力计算代替约束扭转下的杆件应力计算，而自由扭转只能用于圆形截面的等直径杆件计算，所以这是不正确的。

文献[2]详细的介绍了杆件在各种条件下的扭转计算，但没有给出用于工程实践可用的计算公式，本文从强度计算的角度，提出均布扭矩下工字钢梁的扭转应力具体计算公式。可作为对新规范的一种补充。

2 约束扭转计算变量的计算

与自由扭转显著不同的是，约束扭转应力计算出现了双力矩B、主扇性坐标ωn、扇性惯性矩Iω等变量。以下将简单介绍上述各个变量的几何意义和计算方法。

扇性坐标，又称之为扇性面积，之所以称之为坐标是因为它的值与扇性极点和扇性零点的选取有关，选择不同的扇性极点和扇性零点将得到不同的值，故称之为坐标。又之所以称之为面积是因为它的量纲为长度的二次方，与面积是一致的。选择适当的扇性极点和扇性零点可以获得主扇性面积即主扇性坐标。

图1 扇性面积计算微元图

则曲线上任意一点N处的扇性面积为：

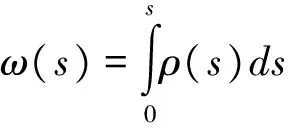
(2-1)

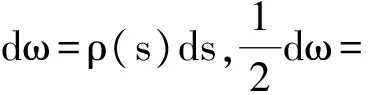
图2 扇性面积计算几何图

根据式(2-1)可以得出：

(2-2)

一般情况下，在选定扇性极点、扇性零点的情况下，对截面简单的杆件，往往以式(2-2)计算某点的扇性面积，因为可以避免积分。

对于任意选定的扇性极点和扇性零点，文献[2]称之为辅助扇性极点和辅助扇性零点。对于约束扭转计算，只有将扇性极点和扇性零点选择在特殊的点上才能正确计算扭转荷载下的截面轴力，及绕截面两个正交坐标下的弯矩。这里为简单起见，不介绍符拉索夫理论，直接给出结论：工字梁主极点为截面的剪切中心，主零点为对称轴与外轮廓线的交点。主极点和主零点下的扇性面积称之为主扇性面积则计算公式如下：

图3 单轴对称工字钢梁截面几何参数

剪切中心O距离B点(主扇零点)公式为：

(2-3)

截面的主扇惯性矩：

(2-4)

(2-4)量纲为长度的6次方。δ为杆件壁厚。注意积分的区域为全截面。

上述公式可在文献[2]中查到，不过文献[2]中(d2-αx)2为(d2-αx)，文献中此处应为作者笔误。

与自由扭转不同的是，约束扭转将沿杆件长度方向引起正应变，即约束翘曲，自由扭转为自由翘曲。约束翘曲将引起截面正应力：

(2-5)

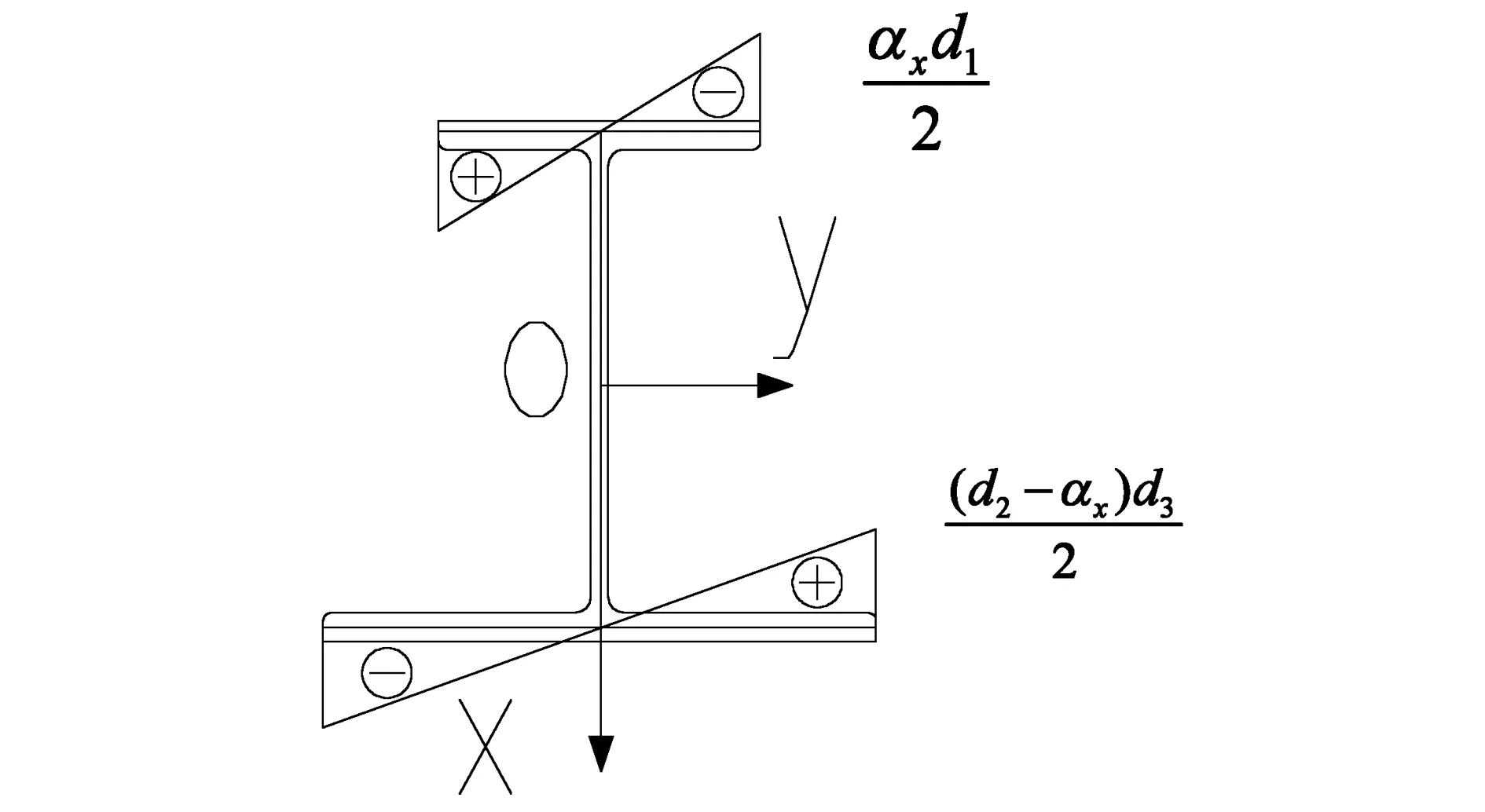
图4 单轴对称工字梁ω(s)分布图

截面的主扇静面积矩：

(2-6)

量纲为长度的五次方，其分布图为(图5).

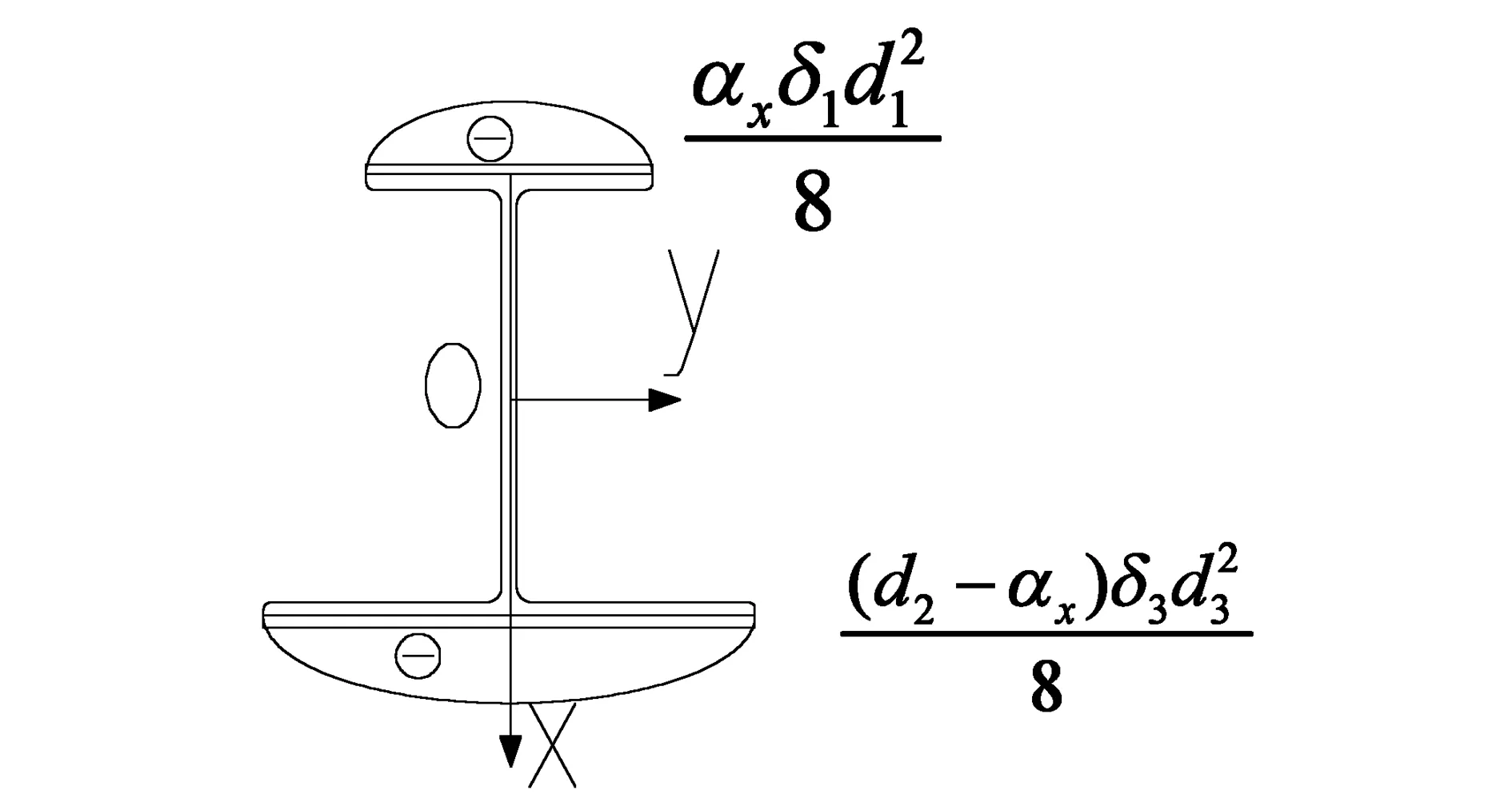
图5 单轴对称工字梁S(s)分布图

3 杆件约束扭转的微分方程及其解

根据文献[2]约束扭转杆件微分方程为：

E1Jωθ‴′(z)-GJdθ′(z)=m(z)

(3-1)

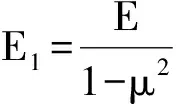
方程(3-1)的解为

(3-2)

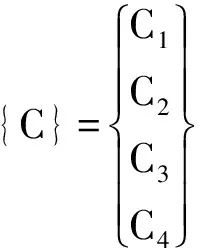
C1、C2、C3、C4为一组常数，根据边界条件确定。

约束扭转的边界条件分为应力边界条件和位移边界条件，其方程为：

杆端扭转角为(3-2)

(3-3)

截面双力矩为：

(3-4)

截面扭矩为：

(3-5)

将(3-1)、(3-2)、(3-3)、(3-4)联立为矩阵：

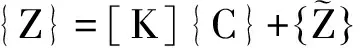
(3-6)

设均布扭矩为均布荷载q在偏离距e下引起：m(z)=qe。则非齐次方程的特解为

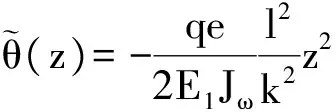
(3-7)

4 满足边界条件的系数及截面应力求解

Z=0端固定，Z=L端铰接：

θ(0)=0、θ(l)=0

θ′(0)=0、B(l)=0

对于给定边界条件的工字梁在均布扭矩作用下的计算过程如下：

由边界条件根据本节边界条件计算C1、C2、C3、C4。系数求解可以采用矩阵计算法，也可以自行推导出关于C1、C2、C3、C4的显式解。

均布扭矩作用下，截面的双力矩分布函数为

(4-1)

则截面的扭矩分布函数为

L(z)=GJd[C2+2z1z]

(4-2)

截面扭转角分布函数为

(4-3)

截面的正应力按下式求解：

(4-4)

σM(z,s)为弯曲正应力，可根据文献[3]求解。

开口截面的薄壁杆件约束扭转截面上的剪应力由两部分组成。一部分是自由扭转剪应力τs；一部分是约束扭转剪应力τω。计算时首先将截面总扭矩分解为两部分弯扭力矩Mω和自由扭转扭矩H。量纲均为Nm。

L(z)=Mω(z)+H(z)

(4-5)

自由扭转扭矩H又称之为圣维南扭矩,其计算公式为：

H(z)=GJdθ′(z)

(4-6)

自由扭转扭矩H引起的截面剪应力可按文献[3]中自由扭转剪应力计算：

(4-7)

δ为壁厚。

弯扭力矩Mω引起的截面剪应力按下式计算：

(4-8)

5 自由扭转与约束扭转计算对比

在两端简支下(扭矩按两端受扭固定)：如果完全按自由扭转计算仅能得到截面的自由剪应力，直接按(4-7)：

而竖向荷载引起的腹板中间的剪应力仅为(按两端简支计算)

因此位于杆件支座处，截面腹板中间的最大总剪力为

τ1+τ2=112.9MPa

采用Q235钢材即可满足设计要求。

如同第一节所述，开口工字钢的扭转为约束扭转，首先按按两端翘曲约束为固定的支座计算扭转应力：

以本节条件计算：

Jω=5.655×1011mm6

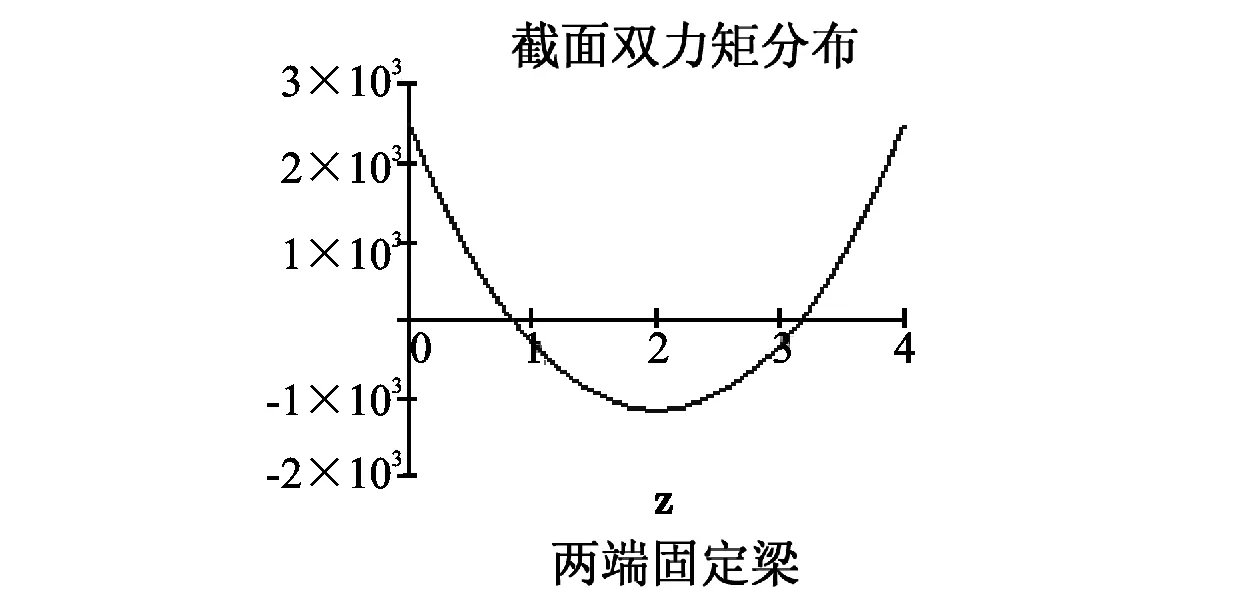
图6 两端固定杆件，双力矩B(z)

其中B(0)=B(4m)=2.484kNm2B(2m)=-1.1755kNm2

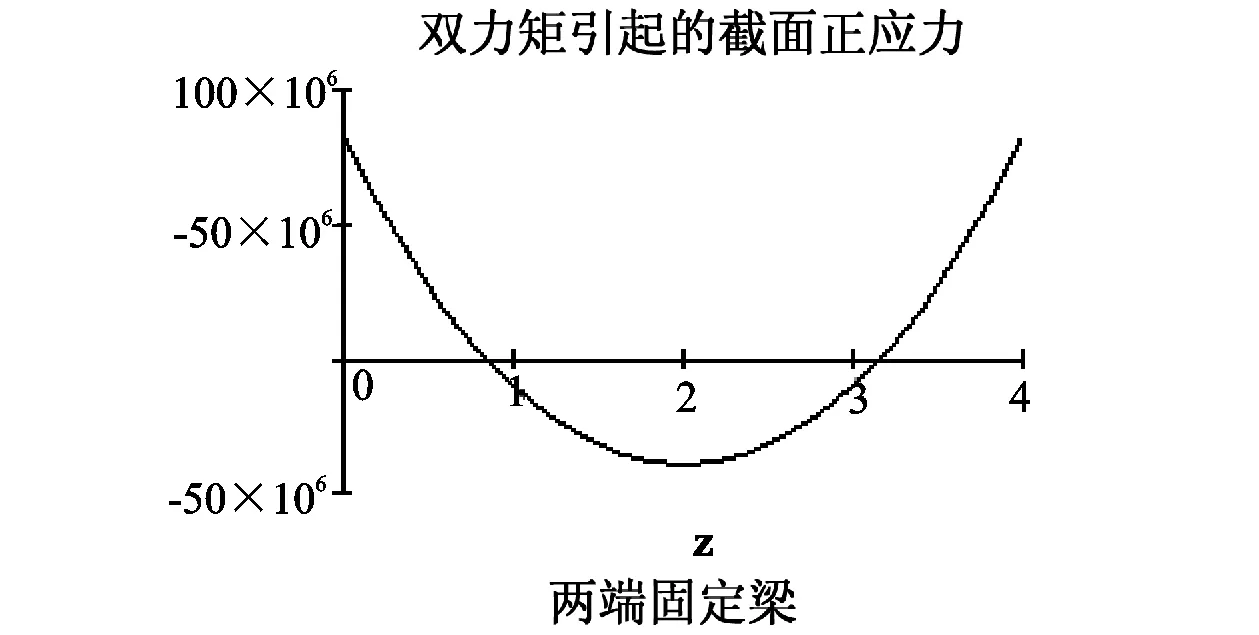
图7 两端固定杆件，沿杆长方向扭转正应力分布

其中σω(0m)=σω(4m)=82.6MPa

σω(2m)=-39.0MPa

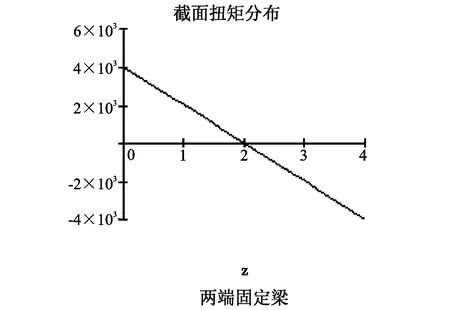
图8 两端固定杆件，沿杆长方向截面总扭矩分布

其中L(0m)=-L(4m)=4kNm

图9 两端固定杆件，沿杆长方向截面自由扭矩分布

其中H(0m)=H(4m)=0kNm

H(1m)=0.254kNm

圣维南扭矩为零，即第一节的Tst——构件截面的自由扭转力矩；开口薄壁截面，不考虑这一项。规范的本意应该是两端固定梁支座处，从图9可以看出 仅在支座处为零，规范未详细注明，有些不妥。

因此支座：Mω(0m)=L(0m)=4kNm

截面B处剪应力为

Sω(B点)=1.127×107mm4

τω(0m,B点)=6.6MPa

接下来将支座条件设为两端允许自由翘曲的铰接支座，其他条件仍按本节，则:

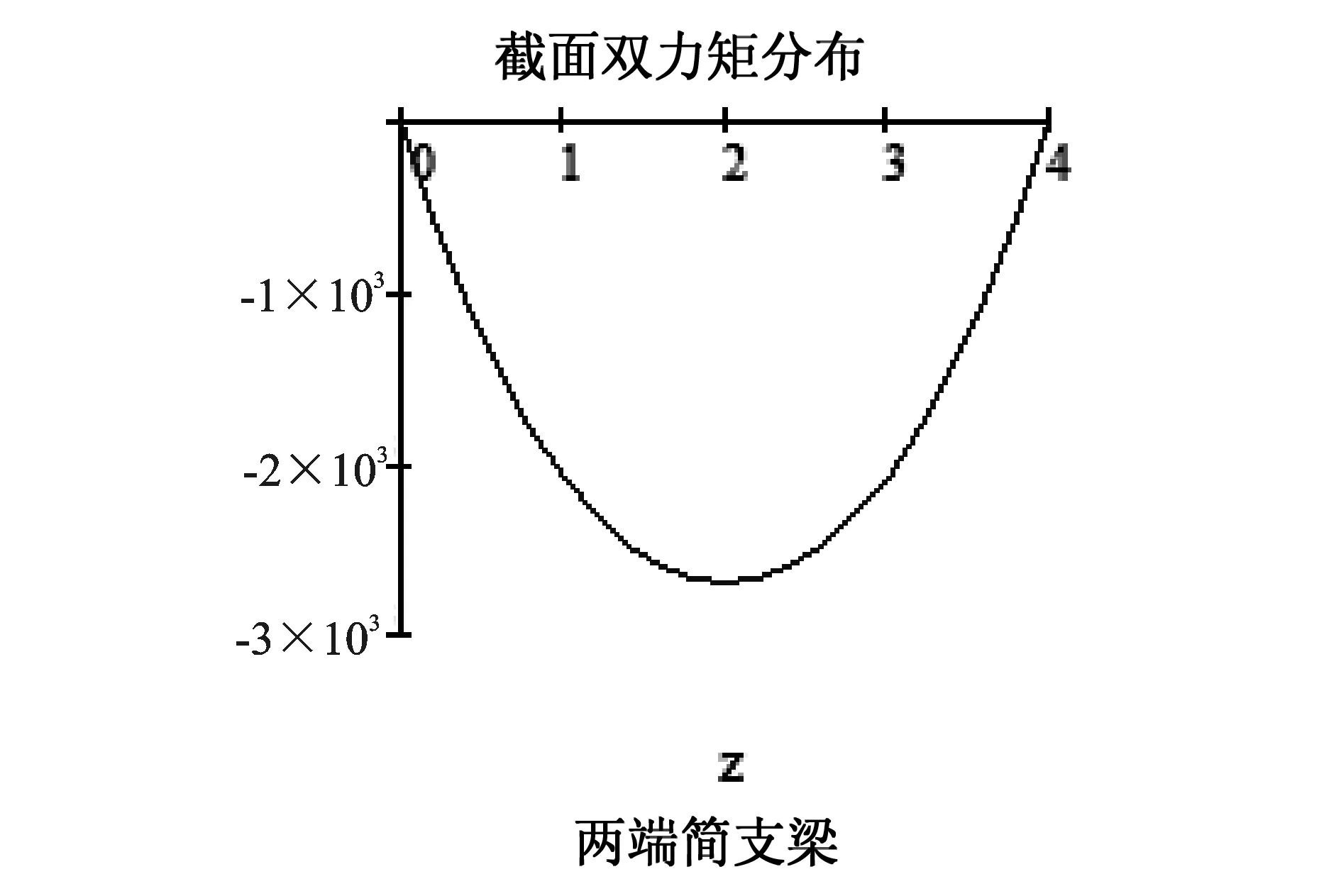
图10 两端铰接杆件，双力矩B(z)

其中B(0)=B(4m)=0kNm2

B(2m)=-2.705kNm2

图11 两端铰接杆件，沿杆长方向扭转正应力分布

其中σω(0m)=σω(4m)=0MPa

σω(2m)=-89.9253MPa

图12 两端简支杆件，沿杆长方向截面总扭矩分布

其中L(0m)=-L(4m)=4kNm

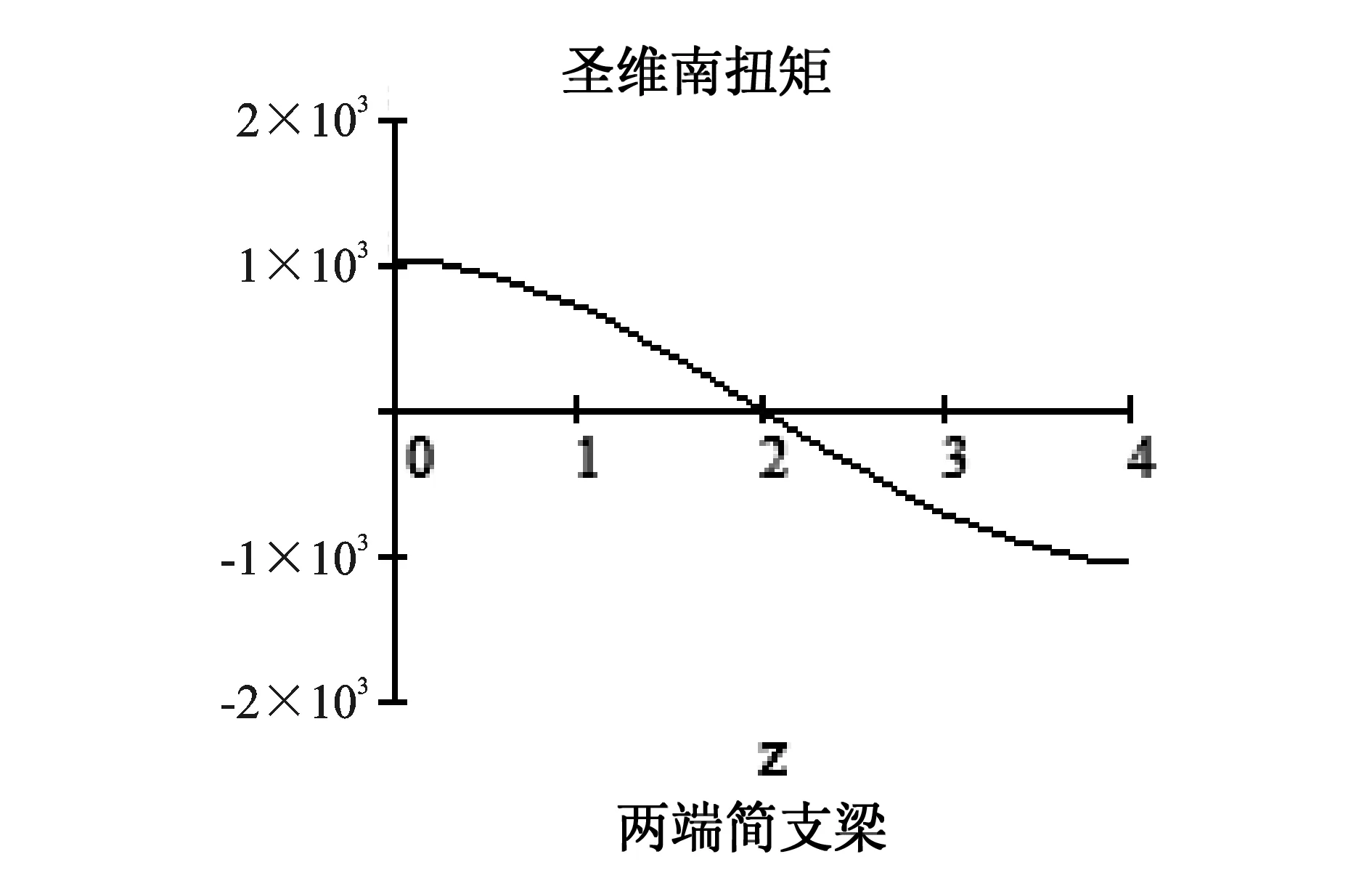
图13 两端铰接杆件，沿杆长方向截面自由扭矩分布

其中H(0m)=-H(4m)=1.0435kNm

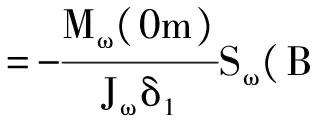
Sω(B点)=1.127×107mm4

τω(0m,B点)=4.9MPa

6 结论

通过这三个算例比较分析，可以得出以下结论：

(1)按约束扭转计算的结果与自由扭转计算结果截然相反，前者杆件将出现较大的正应力，较小的剪应力。而自由扭转计算仅出现较大的剪应力。

(2)即便按支座允许自由翘曲的铰接计算，结果也是同1。

(3)开口截面在实践中不存在完全的自由扭转扭矩。自由扭转扭矩只是一小部分。

(4)在工程实践中，如不按约束扭转计算，杆件将可能因正应力强度不足而引起破坏。

(5)规范忽略开口截面的自由扭矩是因为其数值较小，而不是为零。

[1]GB 50017—201X,钢结构设计规范征求意见稿[S].

[2]包世华,周坚. 薄壁杆件结构力学[M].北京：中国建筑工业出版社. 2006.

[3]孙训方,方孝淑,关来泰. 材料力学[M].北京：高等教育出版社. 1994.

Calculation of Steel I-beam Stress under the Action of Uniform Torque

ZHANGLuchao

(SHANGHAI INSTITUTE OF ARCHITECTURAL DESIGN&RESEARCH.XIAMEN BRANCH,Xiamen 361009)

By giving the calculation principle of calculation parameters on torsion steel I-beam and the calculation method of geometric parameters, this thesis can be a supplement to the forthcoming design code about Steel Structure design Code(GB50017-201X) for helping the designer work. It emphasizes that most engineers doing the calculation of the open section torsion according to free torsion calculation. However, even under the permission of free warping support condition, calculating-I-beam torsion stress is also a kind of restrained torsion calculation.

Sartorial area; Biomet; warpage; free torsion; restrained torsion; stress calculation

张鹭超(1978.2- )，男，国家一级注册结构工程师。

2015-05-26

TU391

A

1004-6135(2015)09-0101-05