一道试题的分析与思考

☉江苏省海门中学 曹亚东

一道试题的分析与思考

☉江苏省海门中学 曹亚东

一、考题

（本题满分16分）如图1所示，公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα=-2.在该块土地中P处有一小型建筑，经测量，它到公路AM、AN的距离分别为3km、km.现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用，问：如何确定B点的位置，使得该工业园区的面积最小？并求最小面积.

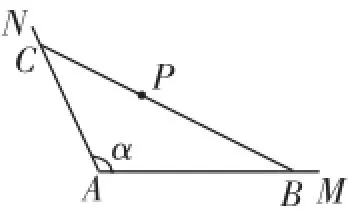
图1

二、命题意图

学生在学习直线与圆时，曾经做过这样的题目：“在直角坐标系xOy中，已知点P（1，3），过点P作一直线l交x轴于点B，交y轴于点C，求△OBC的面积的最小值.”当初学生有三种解法，法1是设斜率k，求出B、C两点的坐标，然后利用直角三角形的面积建立k为变量的函数；法2是设截距式，然后用基本不等式求解；法3是连接OP，把三角形的面积分割成△OBP、△OCP的面积和来求解.为了给高二出一道月考的应用题，决定把上面的原题改编成应用题，另外学生刚刚学习了椭圆，为了考查学生用解析法解题的首要任务就是建立恰当的直角坐标系，所以将y轴绕原点旋转变成y=-2x，为了增加建系的难度，特意将O点改为A点，看看学生是否会选A点为坐标原点.

三、参考答案

解：如图2，以A为原点，AB为x轴，建立平面直角坐标系.…2分

因为tanα=-2，故直线AN的方程是y=-2x.

设点P（x0，y0）.因为点P到AM的距离为3，故y0=3.

图2

所以点P（1，3）.…4分

显然直线BC的斜率存在.设直线BC的方程为y-3= k（x-1），k∈（-2，0）.

从而S有最小值15.

答：当AB=5km时，该工业园区的面积最小，最小面积为15km2.…16分

四、考试结果

全校900多人参加考试，从阅卷的情况来看，平均分为5.15分，12%的学生能完全做对，25%的学生建系不对，30%的学生不会求分式函数的最值，大大出乎笔者的意料.究其原因，主要存在以下几个问题.

1.不会建模

受推导椭圆标准方程建系的影响，有15%的学生以AB所在直线为x轴，其中垂线为y轴来建系，因为AB的长度在变化，这样建系的同学就全军覆没了.还有10%的学生以CB所在直线为x轴，点P为坐标原点来建系，同样是CB的长度在改变，不容易求解.

2.忽视直线BC的斜率的取值范围

因为要使直线BC与AM的交点在第二象限，斜率k必须满足k∈（-2，0），若定义域都忽视了，方法哪怕正确结果也会出错.

3.不会解模

让人眼睛一亮的地方是学生有好几种解法.法1：（求导）目标函数建立如同参考答案.

以下同参考答案.

法2：（二次函数）目标函数建立如同参考答案.时，S取得最小值15.

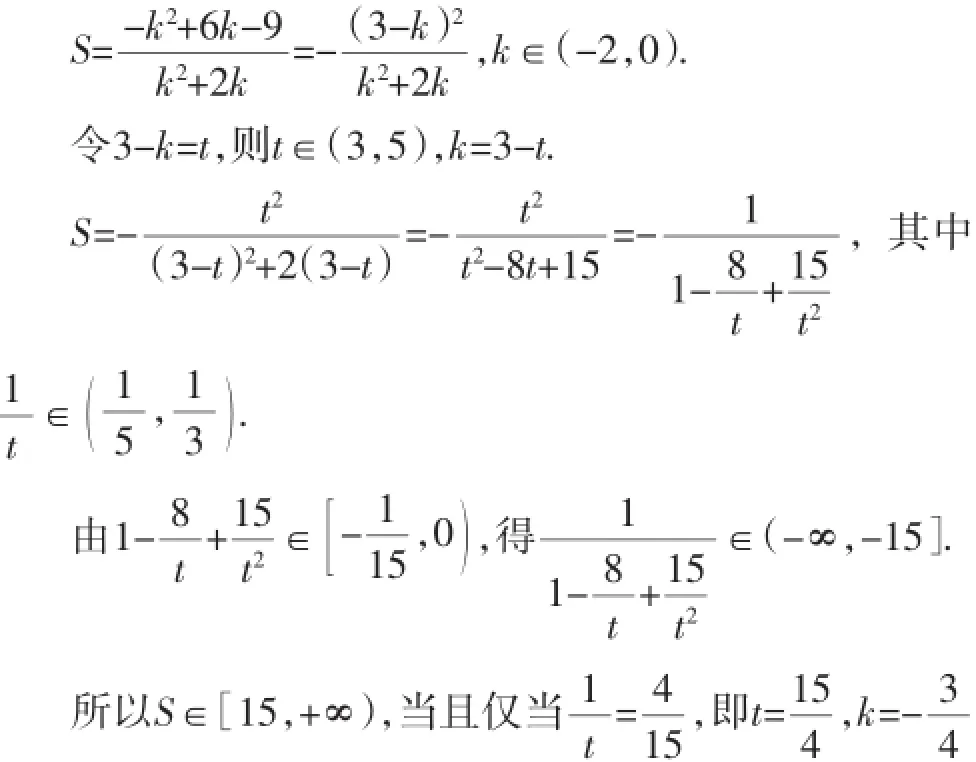
以下同参考答案.

法3：（方程有解）目标函数建立如同参考答案.

（1）在（-2，0）上有一解.

由f（0）=9＞0，得f（-2）＜0，但f（-2）=25＞0，应舍去.

（2）在（-2，0）上有两解.

以下同参考答案.

法4：（基本不等式）.

如图3，过点P作PE⊥AM，PF⊥AN，垂足分别为E、F，连接PA.设AB=x，AC=y（x＞0，y＞0）.因为P到AM、AN的距离分别为3、，所以PE=3，PF=

图3

下同法4.

法6：（几何法寻求约束条件）.

如图2，以A为原点，AB为x轴，建立平面直角坐标系.设AB=m，AC=n（m＞0，n＞0）.用参考答案的方法求得P（1，3）.

下同法4.

尽管解法很多，但本质只有两种.一是用解析法求面积的目标函数，转化为求二次比二次型的分式函数最值，法1和法2是通法，法3不具有一般性，法4、法5较难想到.二是利用等面积法转化为求多变量的最值.法6恰好采用解析法建模，然后转化为求两个变量的最值，可以消元来解，也可以利用基本不等式或柯西不等式来求解.

五、几点思考

1.本题的难点之一在于建系

实际上用解析法解题的基础就是如何建立适当的直角坐标系，适当两字看似简单，运用起来还是有讲究的.很多学生受推导椭圆标准方程建系的影响，关键是没理解椭圆的两个焦点是定点，而这里的A、B两点中B是运动变化的，因此在教学时如果我们能适时地强调两者的区别，那么学生犯这样的错误的机率就小了.

2.本题的难点之二在于解模

3.本题的易错点在于忽视k的取值范围

范围问题是老大难的问题，为此我们要让学生明白检验的重要性，既要检验所得结果是否适合数学模型，又要评判所得结果是否符合实际问题的要求.

总之，将实际问题抽象为数学问题时，要读懂题目，建立数学模型，选择合适的方法，设计合理、简捷的运算途径，这样求出数学问题的解就不难啦！A