性能退化与寿命数据融合的贝叶斯方法研究*
2015-05-05马涛
马涛
(中国飞行试验研究院,陕西 西安 710089)
性能退化与寿命数据融合的贝叶斯方法研究*
马涛
(中国飞行试验研究院,陕西 西安 710089)
针对高可靠性航空产品寿命失效数据样本量小,传统评估方法可信度低的难题,提出基于性能退化数据与寿命失效数据融合的可靠性评估方法。然后用失效机理分析、建模方法选择、失效阀值确定、置信区间求解和数据融合5个关键步骤具体阐述了该方法。最后以飞机液压泵为例,使用该方法进行性能退化数据与寿命数据的融合计算。分析表明,该方法充分利用了性能数据和寿命数据,比传统的方法更加合理,评估结果更加精确。
性能退化;贝叶斯;数据融合;参数估计
0 引言
由于科学技术的不断进步,研制、生产技术以及使用材料的不断提高与改善,产品的可靠性越来越高,寿命越来越长,相对短期内无法获取足够的失效数据,使得通过传统的可靠性分析技术对产品进行可靠性评估面临困难[1]。产品在使用过程中的性能退化数据包含着大量的寿命信息,是可靠性分析一个丰富的信息源。鉴于此,针对传统可靠性分析方法与实际工程应用不相适应的问题,对基于性能退化数据的可靠性分析技术开展研究,解决高可靠、长寿命产品可靠性评估过程中性能退化数据与少量试验寿命数据相结合的实际应用问题[2]。
在性能退化数据的可靠性建模方面,目前国内、外有很多学者已开始进行可靠性评估的研究。主要集中在基于性能退化关系的寿命时间分布、使用仿真的方法得到了基于退化数据可靠性预计的点估计和置信区间、使用退化模型预计了球轴承、滚珠轴承的寿命时间、集成逻辑门可靠性等方面,并在一些实际问题中取得了应用[3-5]。
在基于贝叶斯方法的可靠性建模方面,特别是针对小样本情况下的可靠性评估问题,目前的研究都比较热门。并且,已经出版了一批对贝叶斯方法系统论述的经典论著和学术论文[6-9]。
但是基于性能退化数据与寿命失效数据的数据融合方法的研究仍然处于探索阶段,缺乏有效综合性能与寿命数据的方法[10]。文献[11]充分利用失效物理试验中的性能数据和少量的寿命数据来进行动量轮的可靠性评估,能有效提高可靠性评估的精度。但该模型只解决了从退化量分布的角度进行贝叶斯数据融合的方法。而针对性能退化轨迹的数据与寿命数据融合的问题不能给出良好的解决方案[12]。
本文基于性能退化轨迹进行分析,结合少量寿命数据,利用贝叶斯方法进行数据融合,找到了性能退化与寿命失效数据的数据融合方法。
1 基于性能退化数据的可靠性建模
在现场数据中,部件投入使用的时间不同;观测者记录数据时除故障时间外还有一些部件统计之时仍在完好地工作,形成了现场数据随机截尾的特性[1]。同时,由于科学技术进步,航空部件的可靠性越来越高,寿命越来越长,故障信息样本越来越少,现场的随机截尾数据面临越来越多小样本问题。
因此,在处理小样本的随机截尾数据时,把问题分为2类:一类针对样本量大于10的情况,探索小样本下完全删失数据估计的最佳方法;另一类针对样本量不足10的随机删失数据,采用性能退化数据与寿命数据相融合的贝叶斯估计。其具体流程如图1所示,主要有失效机理分析、建模方法选择、失效阀值确定、置信区间求解和数据融合5个关键步骤,具体如下。
1.1 失效机理分析
失效机理的分析是研究性能退化数据的首要工作。失效机理是引起故障的物理、化学和材料特性等变化的内在原因,收集和分析试验现场产品故障原因将有助于对失效机理的分析和验证,也是为了深入分析故障产生的原因和规律。不同部件在不同的环境下工作的失效机理并不一样,也就可以选择不同的性能退化数据来分析产品的可靠性。
当选择好性能参数后,就可以设计加速试验方案来获取相应的性能退化数据,并对其进行寿命敏感性分析。敏感性分析的主要目的是选取对寿命最敏感的性能参数,以利于下一步更好得分析其性能退化数据。
1.2 建模方法的选择
关于建模方法的选择,可以根据不同的情况作出不同的选择,常见的方法主要有性能参数的分布模型、性能退化轨迹模型与时间序列预测模型3类。
性能参数的分布模型主要考虑了正态分布、对数正态分布和威布尔分布。例如,对于正态分布,认为其性能服从如下:
Y(t)~N(α-βt,σ2),
(1)
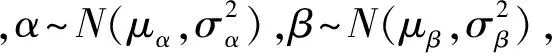
常见的性能退化轨迹模型有线性退化模型、指数退化模型、幂退化模型、对数退化模型和Lloyd-Lipow退化模型等。
时间序列预测模型主要考虑了单指数平滑(single exponential smoothing,SES)方法。SES是指下一期的预测等于前一期的预测加上前一期的预测误差的一个调整,调整系数为α。公式如下:
Yt+1=αXt+(1-α)Yt,
(2)
式中:Xt为观测值;Yt为第t年的预测值;Yt+1为预测值;α为权重,取值为0~1之间。当t=1时,直接采用前一年度的观测值作为本年度的预测值,即Y2=X1。
值得注意的是平滑常数α的选取,一般要运用最小均方差的原则,即在0~1间选取不同的值进行预测,分别计算最小均方差,取其中最小均方差所对应的平滑常数作为正式预测的平滑常数α。

图1 基于性能退化数据与寿命数据融合方法流程Fig.1 Procedure of fusion method based on performance degradation and life data
1.3 失效阈值的确定
退化失效分析中,产品发生失效与否是通过给定的失效阈值进行判定的,当退化量达到失效阈值时产品不再能满足其额定功能要求,即发生失效。一般情况下,失效阈值是给定的一个固定值,即确定性的失效阈值,目前绝大部分的退化失效研究基本上是针对确定性失效阈值的。然而,尽管这种定义及其产生的单点型失效标准简单实用,但有时却不尽合理。实际上,某些产品发生退化失效与否无法用一个确定的量进行判定,即退化失效阈值是一个确定的值,而是一个随机变量,因此也有必要对随机失效阈值下的退化失效问题进行研究。
一个典型的随机失效阈值问题是应力-强度干涉失效模型,当产品所受应力超过产品的强度是时候,产品发生失效。产品应力是一个随机变量,该应力实质上就是产品的失效阈值。另外,如果退化量初始值是随机变量时,相对失效阈值实际上也是一种随机失效阈值。
1.4 置信区间的求解
自助法即是由Bootstrap在1979年首先提出的,是一种再抽样的置信区间求解统计方法。其主要思路为:
(1) 假定观察值便是总体;
(2) 由这一假定的总体进行有放回的样本,即再抽样;
(3) 重复步骤(2),直到抽取到n个自助样本;
(4) 重复步骤(2)与(3),一直抽样B组。
通过以上步骤即可初步计算出可靠性参数,然后再使用Bootstrap方法扩充样本,求出可靠性参数的置信区间与贝叶斯验前分布。
1.5 数据融合
贝叶斯可靠性评估是一种综合经验信息进行可靠性评估的方法。贝叶斯方法假设可靠性指标有一个“先验分布”,这个先验分布一般根据历史资料和经验信息等确定。本文以威布尔分布估算可靠度举例说明。设额定时间τ下的可靠度为R0,则产品寿命分布为
(3)
式中:m为威布尔分布的形状参数。
假设产品性能参数满足正则条件则产品的可靠度函数为
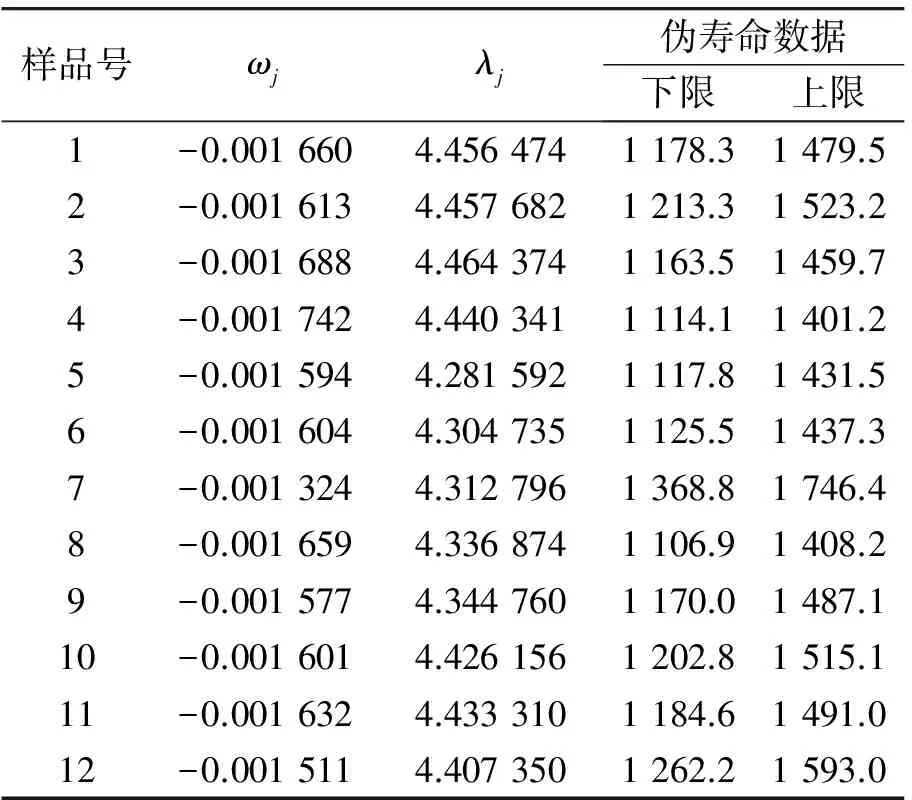
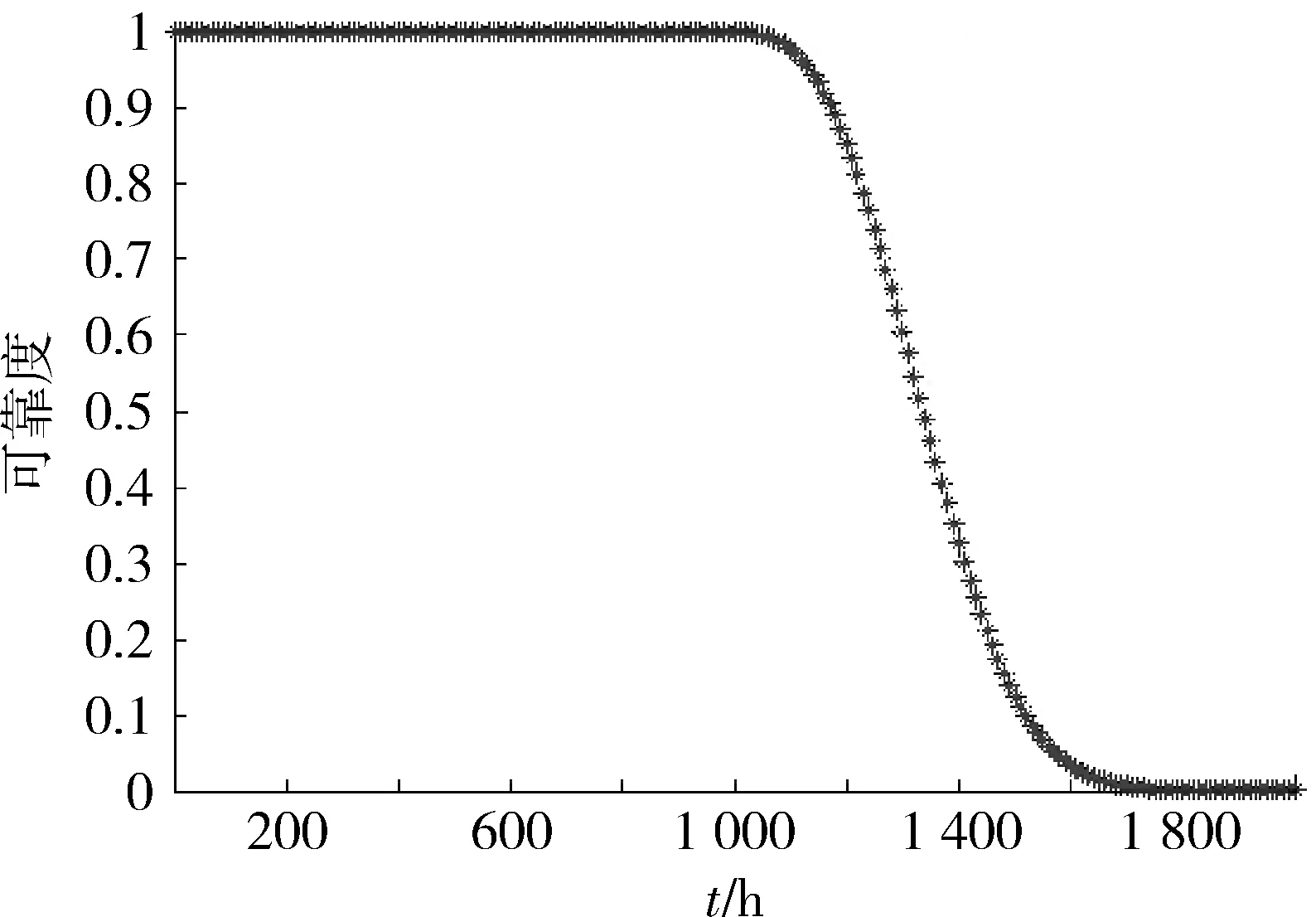
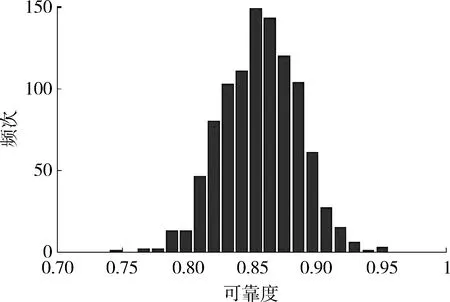
R(t)=1-F(t)=P(Y(t) (4) 式中:Y(t)即为公式(1)中的性能参数随时间变化函数;L为失效阈值,其即可为固定值,也可以为服从一定分布的随机值。 有了可靠度函数R(t)之后就可以利用Bootstrap方法获取额定时间τ下的可靠度密度π(R0)。该密度可以作为寿命分布中R0的验前分布。 基于寿命失效数据,假设其试验的截尾时间为td(d∈S),其中S为无失效试验的集合,失效的截尾时间为tf(f∈F),F为失效试验的集合,则似然函数为 (5) 由专家经验,形状参数m的验前概率密度可取均匀分布,即 π(m)=1/(m1-m2),m1≤m≤m2. (6) 于是,在得R0和m的验前分布之后,按贝叶斯理论,可得R0和m的联合验后分布为 (7) (8) (9) 液压泵是飞机液压传动与控制系统的能源附件,用来向系统提供具有一定压力和流量的油液,把机械能转化为压力能。影响液压泵工作性能的因素中除了一些偶然因素外,其主要失效模式及失效机理为磨损型。综合研究表明,选择液压泵的输出流量或者高温小流量作为液压泵的主要性能退化特征参数,高温小流量的退化最为明显,是液压泵首选的性能退化参数,本研究是以高温小流量作为液压泵性能退化参数。 某型飞机液压泵寿命数据主要有1 423,1 687,869+,759+,1 527+(带+的表示数据有删失)。仅根据上述5个寿命数据不可能用经典方法进行参数估计,采用本文用基于性能退化数据与寿命失效数据进行综合评定。 将以上测得的数据输入程序中,将性能退化数据与五大模型相拟合,结果显示液压泵性能退化数据与线性退化模型拟合程度最高,即yj=ωjtj+λj是液压泵最合适的退化模型。各样品的退化轨迹参数如表1所示。 表1 样品退化参数Table 1 Degradation parameter of sample 则t时刻该液压泵的失效概率为 F(t)=P(T 当t=1 200 h时,代入计算结果,则此时液压泵的可靠度为 R0=1-F(t)=0.851 6. 同时也可计算出用性能退化轨迹模型得出液压泵可靠度曲线如图2所示。 图2 液压泵可靠度曲线Fig.2 Reliability growth curve of fluid pump bootstrap 根据上述原理,基于自助法利用表1中的数据可以计算出1 000个R0,其柱状图如图3所示。 图3 基于自助法的可靠度直方图Fig.3 Reliability histogram based on bootstrap 对直方图进行数据拟合,发现其与正态分布拟合得最好,通过计算可知R0的概率密度函数为N(0.857 1,0.032),即π(R0)~N(0.857 1,0.032)。 另外,由实际经验可得,液压泵的寿命分布数据服从威布尔分布,且对于形状参数m,认为其服从均匀分布,其中m1和m2由专家经验确定得到,认为m1=1,m2=2,即π(m)~μ(1,2)。 计算可得,t=1 200 h时,其可靠度为 在处理小样本的随机截尾数据时,本文针对极小样本量的情况下传统可靠性评估方法可信度低的问题,提出了一种性能退化数据与寿命数据融合的贝叶斯参数估计方法,并详细介绍了该方法使用中的五个关键步骤。最后以飞机液压泵为例,用该方法进行可靠性评估。本文的计算表明: (1) 飞机液压泵的高温小流量退化数据与线性模型拟合最好。并且,当工作时间在1 000 h以内时,其可靠度很高,但在1 000~1 600 h之内,其可靠度迅速下降,直至趋向于0。 (2) 基于性能退化数据与寿命失效数据的数据融合方法充分利用了性能数据和寿命数据,比传统的方法更加合理,评估结果更加精确。 [1] 赵宇.可靠性数据分析[M].北京:国防工业出版社,2011:20-22. ZHAO Yu. Data Analysis of Reliability [M]. Beijing: National Defense Industry Press,2011:20-22. [2] 李金国,傅志国,刘永坚.高可靠性航空产品试验技术[M].北京:国防工业出版社,2011:1-5. LI Jing-guo, FU Zhi-guo, LIU Yong-jian. Test Technology of High Reliability Aviation Product[M]. Beijing: National Defense Industry Press,2011: 1-5. [3] 张永强, 刘琦, 周经伦. 基于性能退化数据的可靠性评定方法研究[J].飞行器测控学报,2005,24(5):54-58. ZHANG Yong-qiang, LIU Qi, ZHOU Jing-lun. Reliability Evaluation Based on Performance Degradation Data[J]. Journal of Spacecraft TT&C Technology, 2005, 24(5): 54-58. [4] 袁亚芹. 基于性能退化数据的航空液压泵可靠性分析[D].南京: 南京理工大学,2009. YUAN Ya-qin. Reliability Analysis of Aircraft Hydraulic Pump Based on Performance Degradeeation Data[D]. Nanjing: Nanjing University of Science and Technology, 2009. [5] 方峻, 魏星, 樊黎霞,等. 基于性能退化数据的航空液压泵可靠性分析[J].机械研究与应用,2008,21(6):30-33. FANG Jun, WEI Xing, FAN Li-xia. Reliability Analysis of Aircraft Hydraulic Pump Based on Performance Degrade-Eation Data[J]. Mechanical Research & Application, 2008, 21(6): 30-33. [6] BERGER J. Statistical Decision Theory and Bayesian Analysis[M]. New York : Spring- Verlag, 1985. [7] CHERNICK M R. Bootstrap Methods: a Practitioner’s Guide [M]. New York : John Wiley & Sons , 1999. [8] 冯静, 周经伦, 孙权. Bayes分析中多源验前信息融合的ML-II方法[J]. 数学的实践与认识,2006, 36(6): 142-145. FENG Jing, ZHOU Jing-lun, SUN Quan. Fusion of Information of Multiple Sources Based on ML-II Theory in Bayesian Analysis[J]. Mathematics in Practice and Theory, 2006, 36(6): 142-145. [9] 李建伟. 试飞阶段系统级平均修复时间验证方法研究[D].西安:空军工程大学,2010. LI Jian-wei. Study on Validation Method of Mean Time to Repair in Test Flight Stage[D].Xi’an: Airforce Engineering University, 2010. [10] 王卓健, 沈安慰, 郭基联. 基于机群仿真模型的平均秩次法有效性分析[J].系统工程与电子技术,2013,35(5): 1128-1132. WANG Zhuo-jian, SHEN An-wei, GUO Ji-lian. Analysis of Validity with Mean Rank Order Method Based on Air Fleet Simulation Model[J]. Systems Engineering and Electronics, 2013, 35(5): 1128-1132. [11] 刘强, 黄秀平, 周经伦,等. 基于失效物理的动量轮贝叶斯可靠性评估[J]航空学报,2009,30(8):1392-1397. LIU Qiang, HUANG Xiu-ping, ZHOU Jing-lun, et al. Failure Physics Analysis Based Method of Bayesian Reliability Estimation for Momentum Wheel[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1392-1397. [12] 沈安慰, 郭基联, 王卓健. 航空装备现场数据可靠性评估方法有效性分析[J].航空学报, 2014, 35(5): 1311-1318. SHEN An-wei, GUO Ji-lian, WANG Zhuo-jian. Validity Analysis of Reliability Evaluation in Aviation Equipment Field Data[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1311-1318. Research on Bayes Parameter Evaluation Based on Performance Degradation and Life Data Fusion MA Tao (Chinese Flight Test Establishment,Shaanxi Xi’an 710089,China) Aiming at the problem that the life failure data of high reliability aviation product is short, and the reliability of traditional evaluation way is low, the data fusion algorithm based on performance degradation data and life failure data is put forward to evaluate the reliability. Then the way is described by five critical steps, namely analysis of failure mechanism, selection for ways building models, the failure threshold selection, confidence interval solving, and the data fusion. In the end, the hydraulic pump on airplane is taken as an example to use this method to calculate the performance degradation data and life data. The results taking full advantage of performance data and life data show that this way is more reasonable and accurate than traditional ways. performance degradation; Bayes; data fusion; parameter evaluation 2014-08-01; 2014-09-26 十二五国防技术基础科研项目(Z052013B004) 马涛(1975-),男,安徽泗县人。高工,硕士,主要研究方向为RMS评估与验证。 通信地址:710089 陕西省西安市73信箱飞行部可靠性研究中心 E-mail:zjsaw@sina.cn 10.3969/j.issn.1009-086x.2015.04.028 V37;O212.8 A 1009-086X(2015)-04-0166-06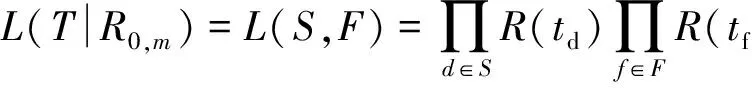
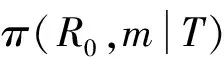
2 算例分析
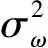
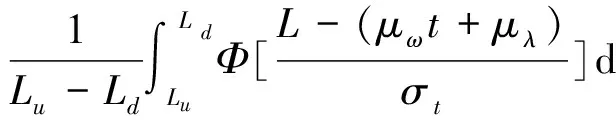
3 结束语
