基于单位脉冲响应的伺服系统带宽仿真研究*

张东云，殷新华，张鑫，王再社

(西昌卫星发射中心，四川 西昌 615000)

基于单位脉冲响应的伺服系统带宽仿真研究*

张东云，殷新华，张鑫，王再社

(西昌卫星发射中心，四川 西昌 615000)

带宽是伺服系统的一项重要指标。为了确定系统是否满足要求，需要定期对包括系统带宽在内的指标进行测试。一般首先测试系统的频率特性，再根据频率特性得到系统带宽。采用一种单位脉冲响应的方法，实现对伺服系统带宽的测试。仿真结果表明，采用单位脉冲响应的方法能减少实验次数，同时得到的系统带宽与理论带宽之间的误差较小。

伺服系统；带宽测试；频率特性；脉冲响应

0 引言

控制系统带宽频率是一项重要的技术指标。伺服系统带宽反应了系统快速性能的好坏，这主要表现在过渡过程品质和伺服带宽之间的关系中，伺服带宽越宽，系统快速性越好[1]。同时，伺服带宽还影响系统跟踪精度和稳定性，为了使系统能够准确的复现输入信号，即具有一定的跟踪精度，要求系统具有高的带宽；但从系统的稳定性考虑时，需要系统具有一定的抑制噪声的能力，系统的带宽又不能过大[2-3]。因此，在系统设计时，需要根据系统要求设计合适的带宽[4-5]。

对于稳定的伺服系统，需要定期对系统的性能进行测试，判断设备是否满足任务要求。对于系统带宽的测试，一般给系统输入不同频率的正弦信号来完成[6]，这样不仅测试时间比较长，而且，正弦运动对系统传动机构有一定的影响，本文在系统频率特性的基础上，采用一种脉冲响应的方法测试系统带宽。

1 控制系统带宽

1.1 频率特性

(1)

式中：Y，X分别为稳态输出、输入正弦函数的幅值。

(2)

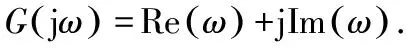
所以频率特性又可表示为

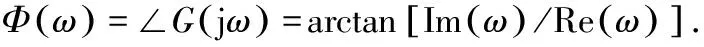
1.2 对数幅相特性

对数幅相特性曲线又称伯德图，是控制系统频率特性的另一种表示方式，对数频率特性曲线的横坐标按lgω分度，单位为rad/s，对数幅频曲线的纵坐标按式(3)线性分度[10]。

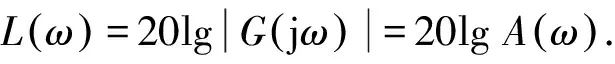
(3)

1.3 系统带宽

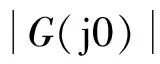
即幅值衰减了3 dB，那么，则定义此时的频率ωb为闭环系统的带宽频率。即当ω>ωb时

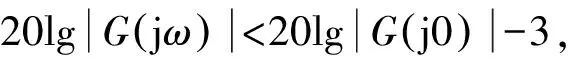
如果系统为典型的一阶或二阶系统，根据文献[10]，系统带宽的计算方法如式(4)和式(5)所示。

对于一阶系统

带宽可表示为

(4)

对于典型的二阶系统

带宽可表示为

(5)

2 控制系统带宽

如果系统由典型环节构成，根据式(4)或式(5)的方法，可以通过数值计算的方法得到系统带宽，但在工程实践中，系统的运动方程形式很难确定，即使已知系统的运动方程，高阶系统的带宽也不容易精确计算。另外，在控制系统使用过程中，系统的参数也会发生一定的变化。因此对于稳定系统带宽的测试，可首先求解系统的频率特性，再确定系统的带宽。

2.1 正弦响应带宽测试

采用实验方法测试系统频率特性原理如图1所示。具体做法是在系统的输入端施加不同频率的正弦信号，然后测量系统的输出稳态响应，再根据幅值比就可以得到系统闭环频率特性[6,11]。

图1 频率特性测试原理框图Fig.1 Diagram of the frequency characteristic testing principle

利用正弦响应测试系统频率特性时，对于一个比较宽频率范围就常常需要对很多不同的频率的值作很多次测量，并且有时候也很难测量输出和输入的相角差。这种测试时间比较长，对于大型系统，正弦测试会对系统的传动机构造成一定的影响。

2.2 脉冲响应带宽测试

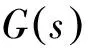
(6)

由式(6)得

(7)

(8)

(9)

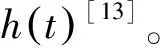
(10)

在式(10)中，对于任何一个固定的ω值，都可以用数值积分的方法算出这个积分。

由于在工程上无法得到理想单位脉冲函数，因此常用具有一定带宽b和有限幅度的矩形脉动函数

来代替。为了得到近似度较高的脉冲响应函数，要求实际脉动函数的宽度b远小于系统的时间常数T，一般规定b<0.1T[10]。

2.3 仿真分析

本文对一典型的二阶角度跟随系统和一高阶天线伺服系统进行仿真实验[10]，分别采用伯德图和脉冲响应的方法对带宽进行分析。

(1) 某角度随动系统的开环传递函数为

(11)

(2) 某天线和驱动的传递函数为

(12)

控制器传递函数为

(13)

由于系统频率特性频率定义与实验法测试带宽原理相同，本文仿真用伯德图来反应系统频率特性。如图2，3所示。

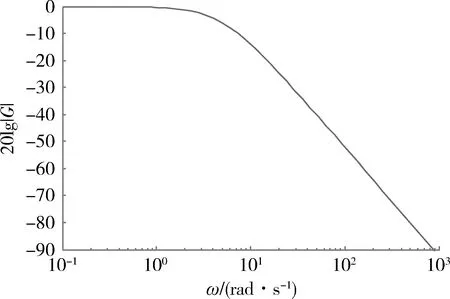
图2 角度跟随系统bode图Fig.2 Bode diagram of angle following system

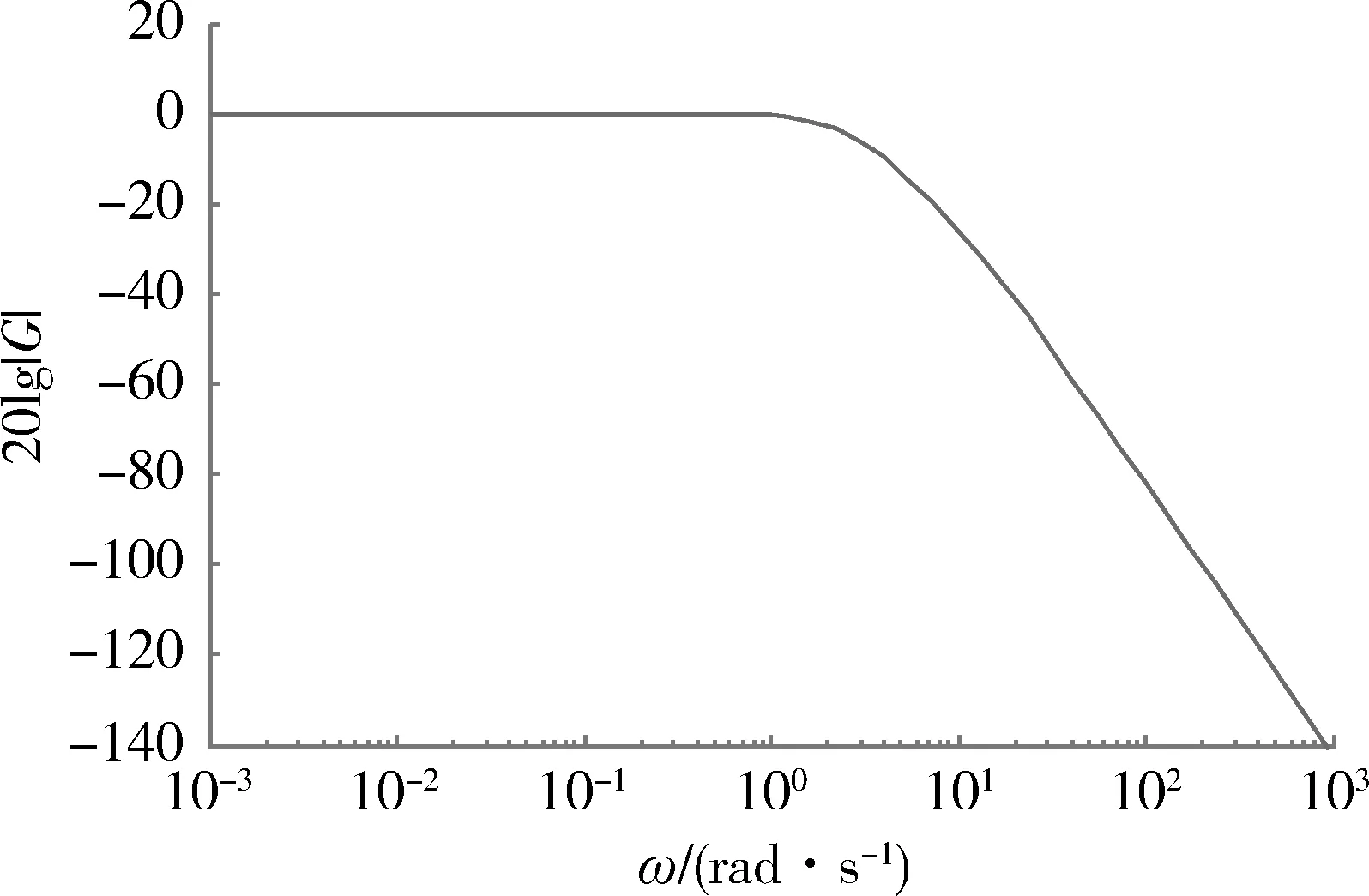
图3 天线伺服系统bode图Fig.3 Bode diagram of Antenna servo system

系统脉冲响应频谱曲线如图4，5所示。

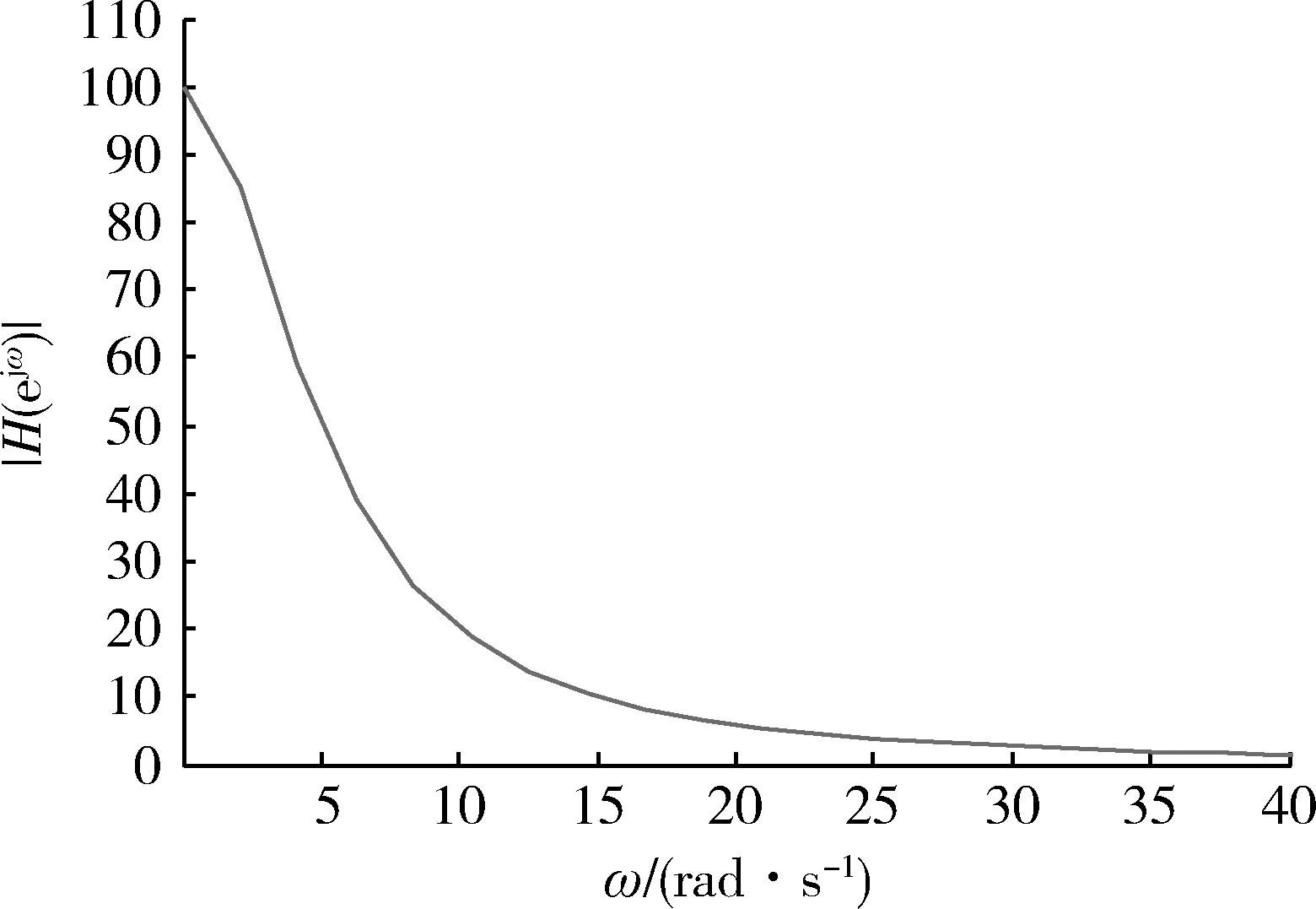
图4 角度跟随系统脉冲响应频谱Fig.4 Impulse response spectrum of angle following system

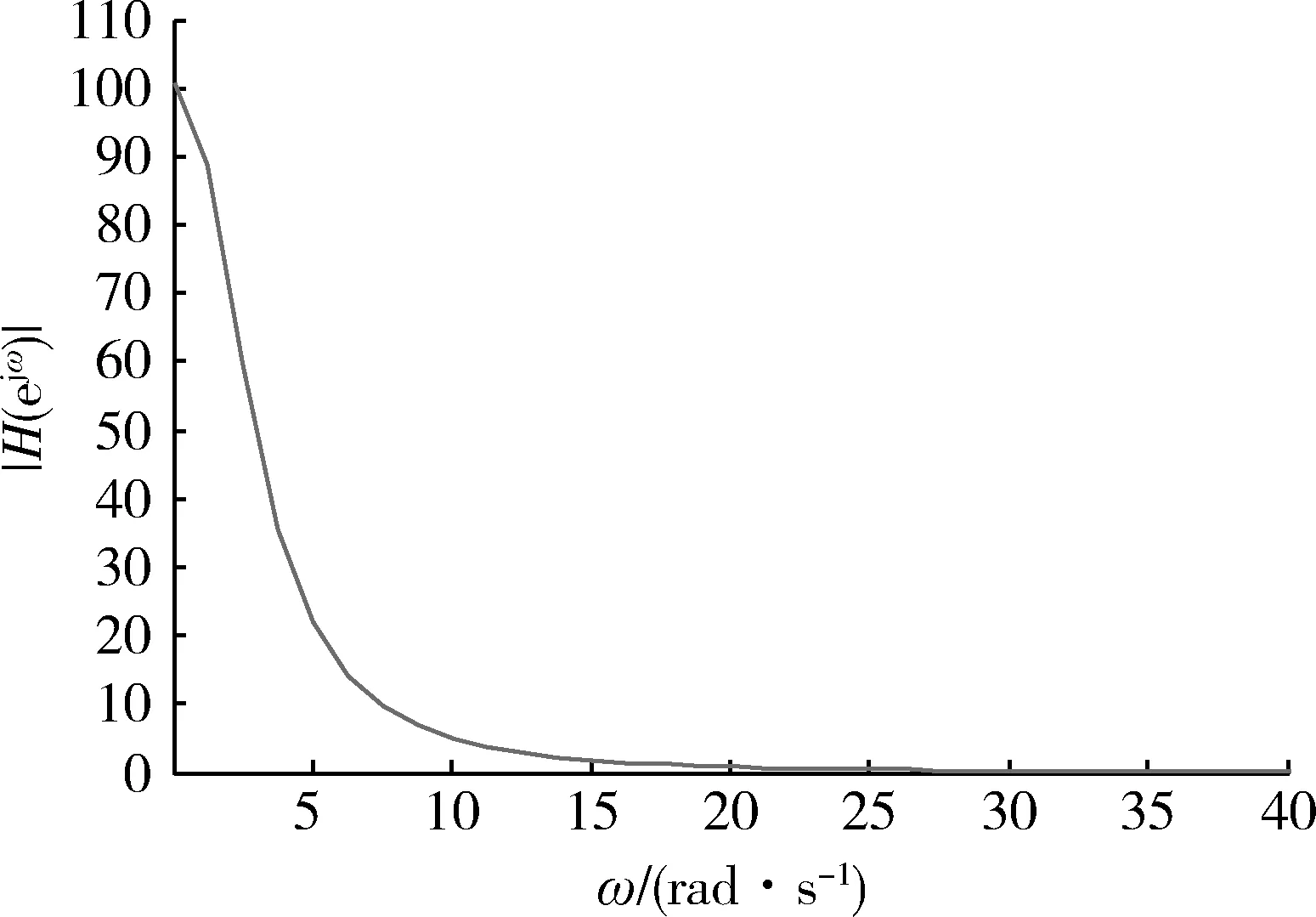
图5 天线伺服系统脉冲响应频谱Fig.5 Impulse response spectrum of Antenna servo system

对于式(11)所示的位置伺服系统，计算得到系统带宽为3.22 rad/s，仿真得到系统的幅相特性曲线和脉冲响应频谱图如图2和图4所示，在图2中，当幅值下降到-3 dB时得到系统带宽为3.22 rad/s，图4中当幅值下降为零频率幅值的0.707倍时得到带宽频率为3.24 rad/s。在式(12)和(13)所示的天线伺服系统中，通过实验对带宽进行测量，由图(3)bode图可知系统带宽为2.03 rad/s，由图5脉冲响应得到系统带宽为2.01 rad/s，通过脉冲响应测试系统带宽与理论值及传统实验方法得到的带宽之间误差较小。

3 结束语

在分析带宽计算测试原理的基础上，针对某天线伺服系统，采用脉冲响应对系统频率特性进行了测试，通过计算结果、系统闭环波的图和脉冲响应测试结果对比，采用脉冲响应方法得到的系统带宽误差较小，同时减少了系统测试次数。

[1] 李连升.雷达伺服系统[M].北京:国防工业出版社,1983. LI Lian-sheng.Radar Servo System [M]. Beijing:National Defence Industry Press, 1983.

[2] 史俊冬.伺服带宽与跟踪性能的仿真研究[J].电子工程师，2004,30(9):4-5,16. SHI Jun-dong.Simulation Study on Servo Bandwidth and Tracking Performance [J].Electronic Engineer, 2004,30(9): 4-5,16.

[3] 万宗奎,宋彦达.一种舰载测量雷达伺服回路分析和设计,信息技术2013,37(12):166-199. WAN Zong-kui,SONG Yan-da. A Design and Analysis for Servo Loop on Naval Ship-Based Measuring Radar[J]. Information Technology, 2013 ,37 (12): 166-199.

[4] 刘锡明,刘立人,孙剑锋,等.星间激光通信中复合轴系统的带宽设计研究[J].光学学报,2006,26(1):101-106. LIU Xi-ming,LIU Li-ren,SUN Jian-feng,et al.Bandwidth Design of Composite Axis System in Satellite Laser Communication [J].Acta Optica Sinica,26(1):101-106.

[5] 曾鸣,张东纯,苏宝库.伺服转台高精度控制系统带宽设计的探讨[J].中国惯性技术学报,2001,6(2):55-59. ZENG Ming,ZHANG Dong-chun,SU Bao-ku.Bandwidth Design of High Precision Control System for Servo Turntable[J].Journal of Chinese Inertial Technology,2001,6(2):55-59.

[6] 唐波,唐小琦,宋宝,等.基于HNC-8数控系统伺服频率特性测试系统的研究[J].液压与机床,2012,40(21):1-3,18. TANG Bo,TANG Xiao-qi,SONG Bao,et al.Research on Implementation of Servo Frequency Characteristic Test System Based on HNC-8 CNC[J].Machine Tool & Hydraulic, 2012,40(21):1-3,18.

[7] 潘良高,王经甫.电液伺服系统频率特性测试系统的设计[J].自动化技术与应用,2009(3):93-95. PAN Liang-gao,WANG Jing-fu.A Frequency Response Testing System for the Electro-Hydraulic Servo System [J]. Techniques of Automation and application, 2009(3):93-95.

[8] 游志平,郭铁轩,何方.伺服系统时域特性与频域带宽的研究[J].计算机测量与控制,2007,15(2):224-225,244. YOU Zhi-ping,GUO Tie-xuan,HE Fang.Study on Servo Frequency domain bandwidth Algorithm via Time Domain Characteristic[J].Computer Measurement & Control, 2007,15(2):224-225,244.

[9] COGGER N D,WEBB R V.Frequency Response Analysis [R]. Hampshire: Solartron Group Ltd., 1997.

[10] 胡寿松.自动控制原理[M].北京:科学出版社,2007. HU Shou-song.Automatic Control Theory [M].Beijing:Science Press,2007.

[11] 王春峰，黄一敏.一种实现舵机带宽测试的系统辨识方法[J].飞行器测控学报，2005,24(1):68-71. WANG Chun-feng,HUANG Yi-min.An Application of System Identification in Testing the Bandwidth of Actuator[J].Journal of Spacecraft TT&C Technology, 2005,24(1):68-71.

[12] 胡广书.数字信号处理理论、算法与实现 [M].北京:清华大学出版社,2003. HU Guang-shu.Digital Signal Processing Theory,Algorithm and Implementation [M].Beijing:Tsinghua University Press , 2003.

[13] 钱学森，宋健.工程控制论[M].北京：科学出版社，2011. QIAN Xue-sen,SONG Jian.Engineering Cybernetics[M].Beijing:Science Press,2011.

Test of Servo System Bandwidth Based on Unit Impulse Response

ZHANG Dong-yun, YIN Xin-hua,ZHANG Xin,WANG Zai-she

(Xichang Statellite Launch Center,Sichuan Xichang 615000,China)

The bandwidth is an important performance requirement for the servo system. In order to determine whether its performance is acceptable for required properties, the test of indicators including bandwidth need to be tested. Generally, test the system frequency characteristic first; finally the bandwidth is got according to frequency characteristic. A method of unit impulse response is used, which realizes the test of bandwidth for servo system. The results show that the number of experiments is reduced by adopting this method. At the same time, the errors between the bandwidth of simulation and theoretical bandwidth are very small.

servo system; bandwidth test; frequency characteristic; impulse response

2015-01-10；

2015-03-02

张东云(1984-)，男，甘肃静宁人。助工，硕士，主要从事控制理论与应用方面的研究。

通信地址：571126 海南省海口市美兰区白驹大道69号 E-mail：zdy20044909@sina.com

10.3969/j.issn.1009-086x.2015.04.035

TP202；TP391.9

A

1009-086X(2015)-04-0210-05