工业平缝机刺布挑线机构的平衡优化设计

郭 莹， 曹巨江*， 张科宇

(1.陕西科技大学 机电工程学院， 陕西 西安 710021; 2.西安建筑科技大学 理学院， 陕西 西安 710055)



工业平缝机刺布挑线机构的平衡优化设计

郭 莹1， 曹巨江1*， 张科宇2

(1.陕西科技大学 机电工程学院， 陕西 西安 710021; 2.西安建筑科技大学 理学院， 陕西 西安 710055)

随着科学技术的发展，工业缝纫机日益向高速、高效、精密和自动化等方向发展.为了满足内部结构静动态特性的要求，针对高速工业平缝机中产生振动的关键机构——刺布挑线机构，应用复矢量法推导出了该机构的总质心轨迹方程以及总惯性力方程，并通过平衡分析对零件进行了结构优化，还使用MATLAB对优化前后的机构进行了对比分析从而证明该优化方案的可行性.优化结果表明，该优化方法部分地平衡了刺布挑线机构在高速运转中所产生的强惯性力，有效地改善了高速平缝机整机的动态性能.

高速工业平缝机; 刺布挑线机构; 平衡分析; 结构优化

0 引言

现代缝制设备缝速不断升级，在高速运转下，周期性变化的强惯性作用力是产生机械振动、噪音和疲劳等现象的主要原因，其结果影响了机构的运动和动力特性[1].刺布挑线机构是缝纫机内部最主要的激励源,同时也是高速工业平缝机的主要机构之一[2].对该机构进行运动分析、惯性力分析及平衡优化设计是改善其动态性能及降低整机振动噪声的有效手段和研究方法.

目前,使用矩阵法、杆组分析法等解析法对机构进行运动分析、动力学分析已有了大量的研究，质量代换法中的静代换法在平衡优化设计中也得到了广泛地应用[3].本文提出的方法是基于机构位置方程和复矢量法求解平面六杆机构的质心运动轨迹以及惯性力幅值的变化规律,应用最优化设计的理论，以降低总惯性力为优化目标，对该机构部分零件的质量、质心位置参数等进行了平衡优化设计.

1 刺布挑线机构的运动分析与惯性力分析

工业平缝机是一个多激励、多响应的复杂机构，在高速工作时整机存在严重的振动.其中，刺布挑线机构运动的动不平衡是引起振动的主要原因.该机构是由对心曲柄滑块机构和四连杆机构等组成的平面六杆机构，具体如图1所示.电机通过主轴将动力传给原动曲柄，分别驱动四连杆机构和曲柄滑块机构相应实现挑线功能和刺布功能.六杆机构的结构和尺寸参数确保挑线和刺布的运动规律以及两者之间的协调配合关系[4].

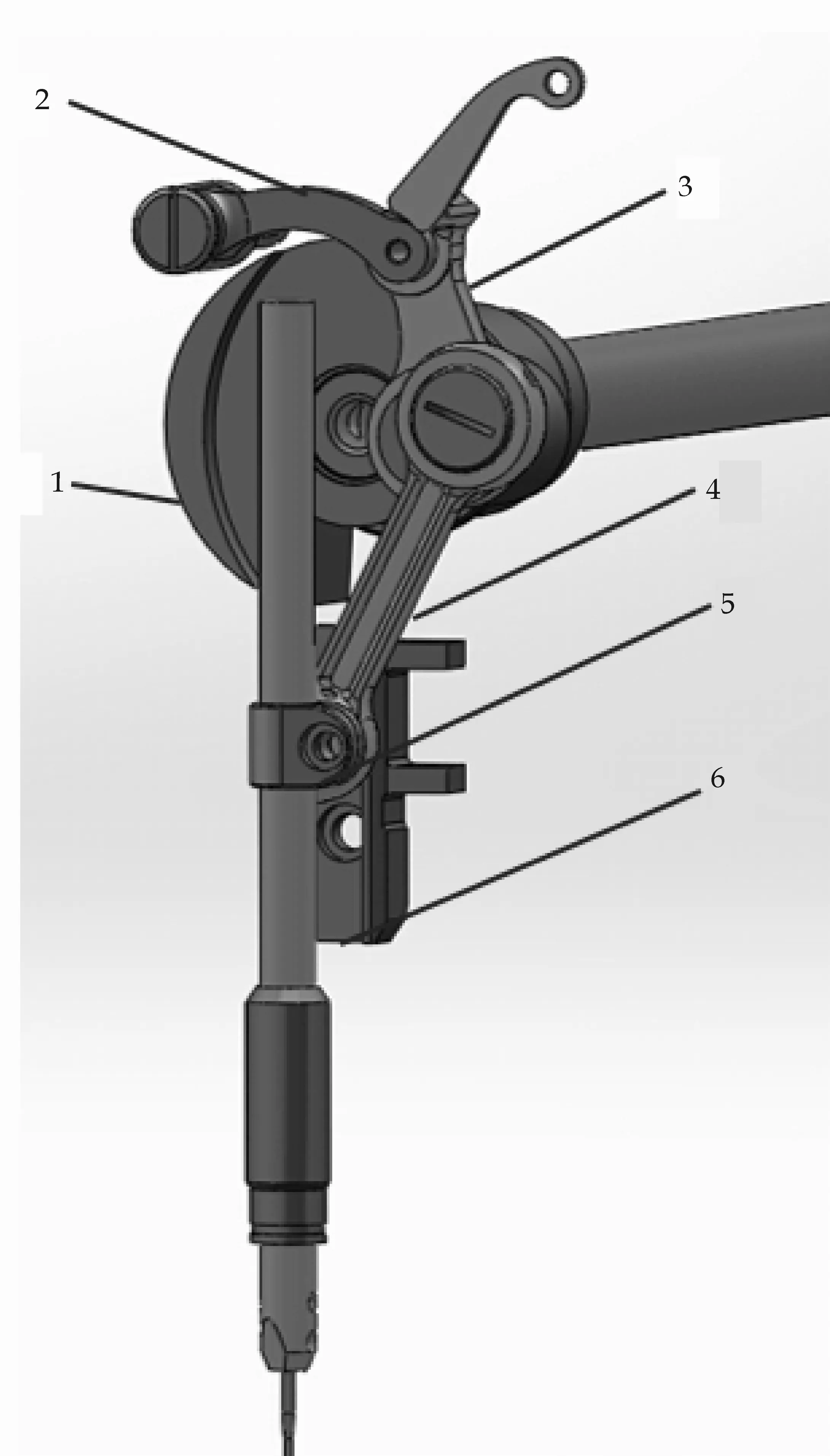
1.曲柄 2.摇杆 3.挑线连杆 4.针杆连杆 5.滑块与针杆 6.机架

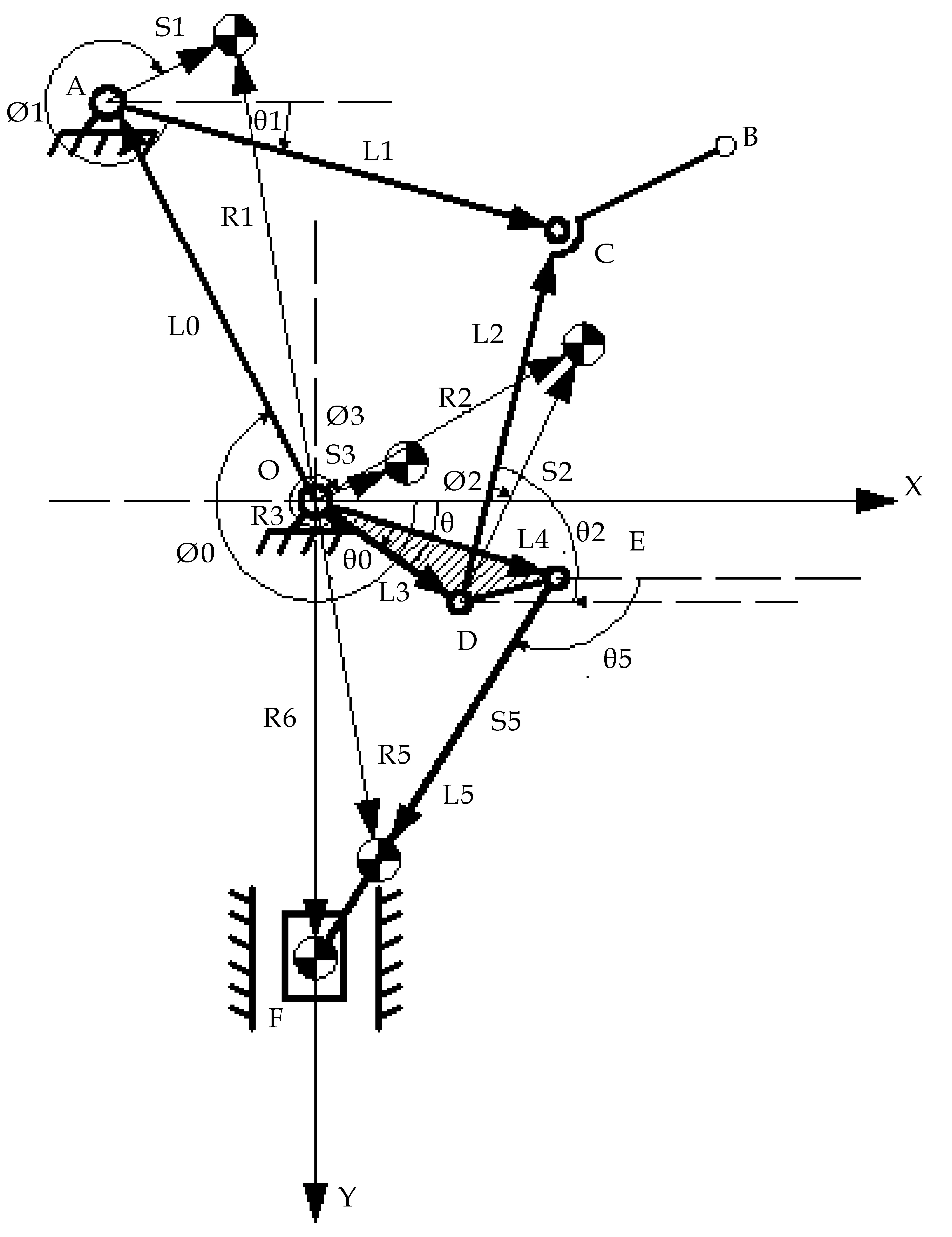
图2 刺布挑线机构的运动简图

根据对刺布挑线机构实际工作中影响因素的分析和要求，对机构分析设定以下条件：

(1)各个运动副的摩擦力及内部间隙忽略不计.

(2)各个构件抽象为刚体，忽略变形对平衡及运动状态的影响[5].

(3)一些构件特征在机构运动分析过程中影响很小，可以忽略不计.

如图2所示，刺布挑线机构是由曲柄滑块机构DEF和四连杆机构ACDO组成的平面六杆机构.建立直角坐标系，取O为坐标原点，其中Li为各构件的矢量表示,li为Li对应的长度；Si为各构件运动副指向质心的矢量,si为Si对应的长度;θ、θi为Li与X轴之间的夹角，是关于时间t的函数，表

示为某时刻构件的运动位置；φ0为L0与X轴之间的夹角，为常量；φi为Li与Si之间的夹角，为常量，表示为各构件质心相对于各构件的位置夹角.

假定原动曲柄以n=4 000 r/min(ω=419 rad/s)做匀速转动,根据复矢量法建立各构件质心运动位移的矢量表达式如下:

R1=L0+S1=l0eiφ0+s1ei(θ1+φ1)

(1)

R2=L3+S2=l3eiθ+s2ei(θ2+φ2)

(2)

R3=S3=s3ei(θ+φ3)

(3)

R5=L4+S5=l4eiθ4+s5eiθ5

(4)

R6=L4+L5=l4eiθ4+l5eiθ5

(5)

相加得出机构总质心的轨迹表达式为:

(6)

式(6)中：mi为各构件质量.

进而推导得出机构的总惯性力表达式为:

(7)

在SOLIDWORKS建立刺布挑线机构的三维模型，并赋予相应的材质可求解质心的位置，同时得到所需的各参数.各参数值如表1所示.

表1 优化前已知参数

EF杆长l5/m摇杆回转半径s1/m挑线连杆回转半径s2/m曲柄回转半径s3/m针杆连杆回转半径s5/mL0与X轴夹角ϕ0/radL1与S1夹角ϕ1/radL2与S2夹角ϕ2/radL3与S3夹角ϕ3/radL3与L4夹角θ0/rad0.048500.009900.016600.005300.028304.188406.184200.151406.058100.15330

代入各参数，利用MATLAB编程得出机构总质心轨迹图、总惯性力幅值图，分别如图3～4所示.

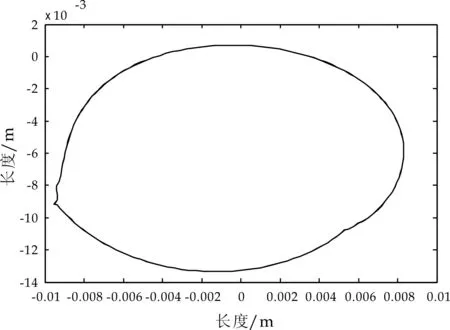
图3 刺布挑线机构总质心运动轨迹图

图4 刺布挑线机构总惯性力曲线图

由图3～4可看出,机构总惯性力呈周期性变化，变化范围为100 N至1 300 N，曲线显示前2/3个周期内总惯性力较小，后期总惯性力突增，达到峰值1 300 N.在周期运动中，刺布机构会配合快速的挑线动作，其中滑块具有很大的加速度，其惯性力的大小对总惯性力影响很大，该机构短时间内完成下针的加速、减速到回针的加速、减速等使滑块加速度突变,从而造成总惯性力的突增[6].

随着工业平缝机的不断高速化，机构总惯性力会随着转速的提高而增大，从而加大整机的振动和运动副的磨损[7].因此,降低机构的总惯性力对于改善刺布挑线机构的振动状况、降低高速平缝机整机的振动和噪音等至关重要.

2 刺布挑线机构的平衡分析

针对刺布挑线机构的振动和动力平衡问题，从作用在机架上的惯性力以及惯性力矩平衡的原理出发，以减轻惯性力产生的动载荷为目的，对六杆机构整体进行惯性力平衡，通过改变机构的质量分布，使机构总质心位置在理想状况下保持固定，即机构总惯性力得到了平衡[8].

由机构总质心表达式(6)可知，若使总质心位置固定，即质心运动方程不随时间变化，只需各构件对坐标原点O的总质量矩为常数.机构总质量矩表达式为：

m2[l3eiθ+s2ei(θ2+φ2)]+m3[s3ei(θ+φ3)]+

m5[l4eiθ4+s5eiθ5]+m6[l4eiθ4+l5eiθ5]

(8)

由于四连杆机构中挑线连杆质量小，结构复杂，而曲柄滑块机构中针杆连杆运动空间受限[9]，对其进行改进难度大，效果不明显.因此,我们选择挑线连杆和针杆连杆为确定杆件，利用质量重新分配的方法对曲柄和摇杆进行改进.由于六杆机构在实际运动中受到结构的限制，机构总惯性力的完全平衡在现实中很难实现，因此优化目标是令质心运动区域尽可能地缩小，从而改善原有机构的动力学特性以达到优化目的.

由图2可知：

θ4=θ-θ0

(9)

由四杆机构的位置矢量方程得到：

(10)

将式(9)、式(10)分别代入式(8)整理可得：

m3s3eiφ3+m2l3+m5l4+m6l4)eiθ+

(m5s5+m6l5)eiθ5

(11)

由于针杆连杆5为非优化构件，并且根据理论分析得知该构件对总质心和总惯性力影响不大，因此不考虑θ5对总质量矩的影响.根据线性独立矢量法，为使总质量矩为常数，则应使与总质量矩中的时间t有关的两个变量θ、θ1的系数项为0[10,11],从而得到惯性力平衡条件为：

(12)

整理式(12)可得到：

(13)

式(13)为平衡机构总惯性力时曲柄、摇杆所需的质径积的总量.为了确定新增加的平衡质量的大小、位置，还需要减去各构件原有的质径积[12].

3 构件的结构优化

本文选取构件1(摇杆)和构件3(曲柄)作为优化对象,以两构件质径积最接近平衡条件为优化目标，最终确定m1、m3、s1、s3、φ1、φ3等共6个独立参数作设计变量.优化计算利用Matlab6.0优化工具箱中的fmincon函数完成.该函数采用序列二次规划法(SQP)求解约束优化问题[13].具体计算流程如图5所示,设计变量的初始值、约束域及优化结果等如表2所示.

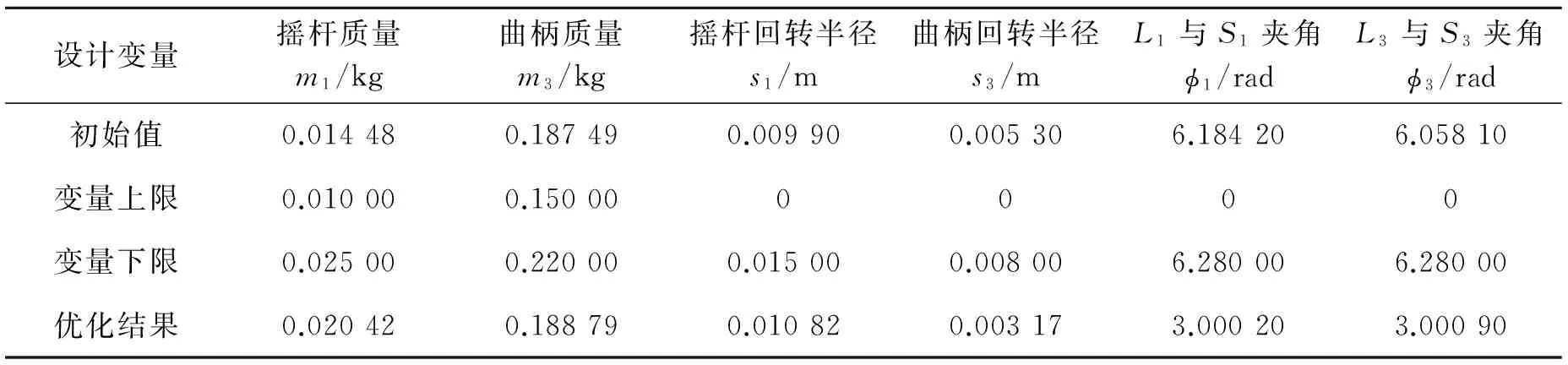
表2 设计变量的初始值、约束域及最优值

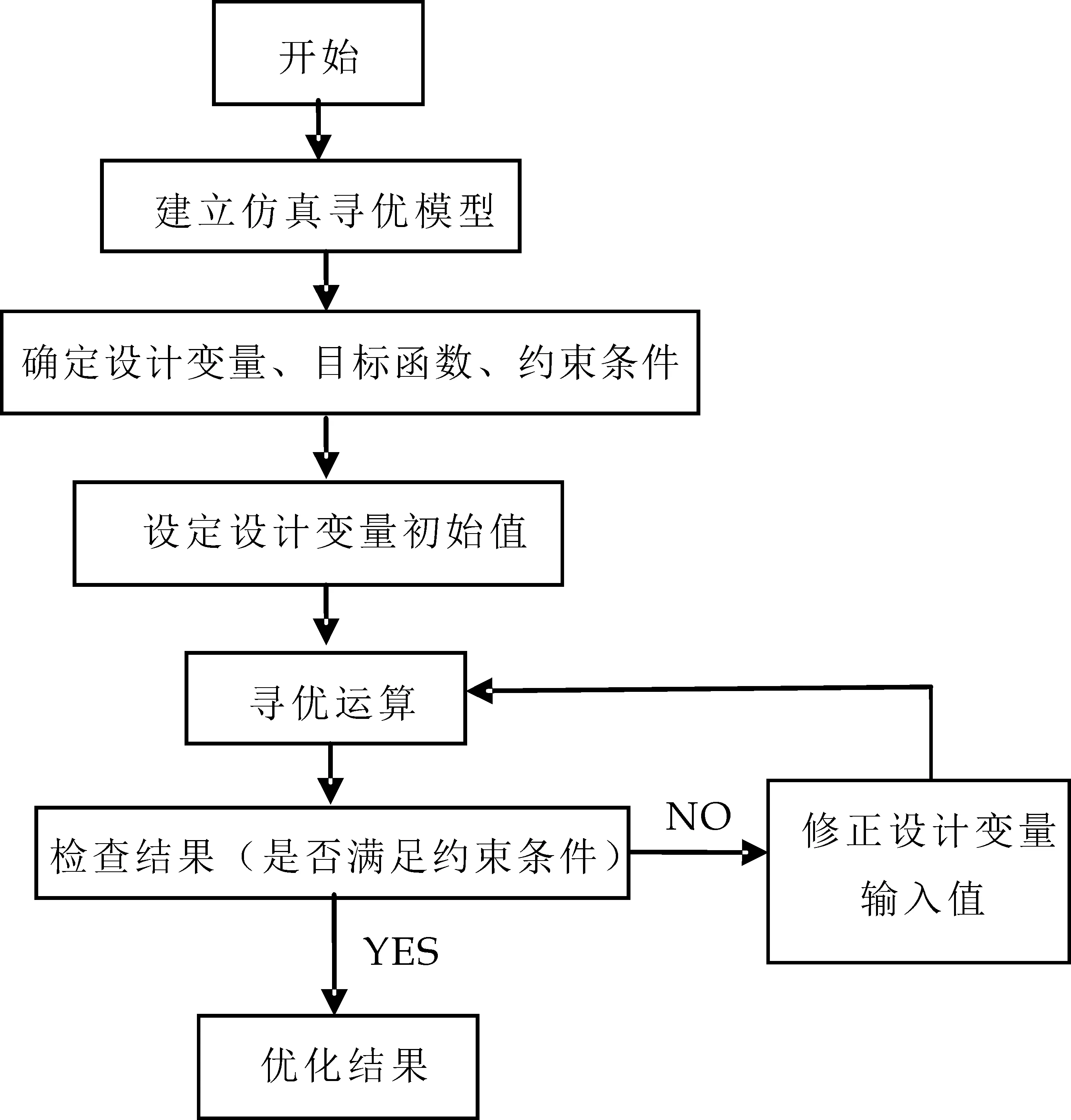
图5 计算流程图

基于本文对刺布挑线机构的平衡分析，在不改变原有机构的结构形式和运动规律前提下，考虑优化构件的实际形状以及运动空间的影响，可采用质量重新分配方法对曲柄以及摇杆进行结构上的修改，从而改变曲柄以及摇杆的质量大小和质心位置，使质径积更加接近目标值，最终部分地平衡其惯性力作用[14,15].

如图6所示,摇杆的优化即在原摇杆下方铰链处沿摇杆反方向增加部分材料;如图7所示,曲柄的优化即在原曲柄A处减少部分材料、B处增加部分材料.

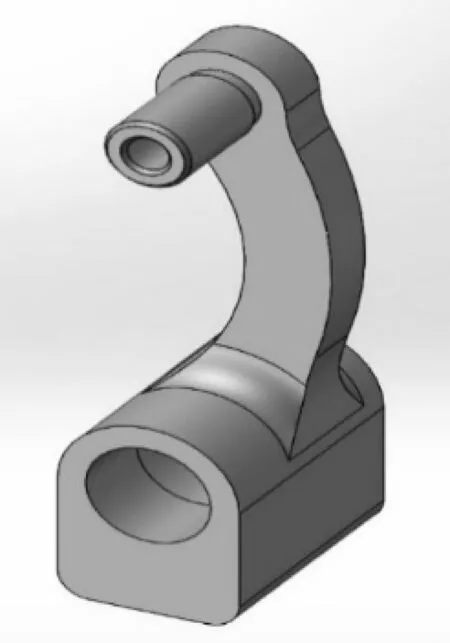
图6 优化后摇杆的三维模型图

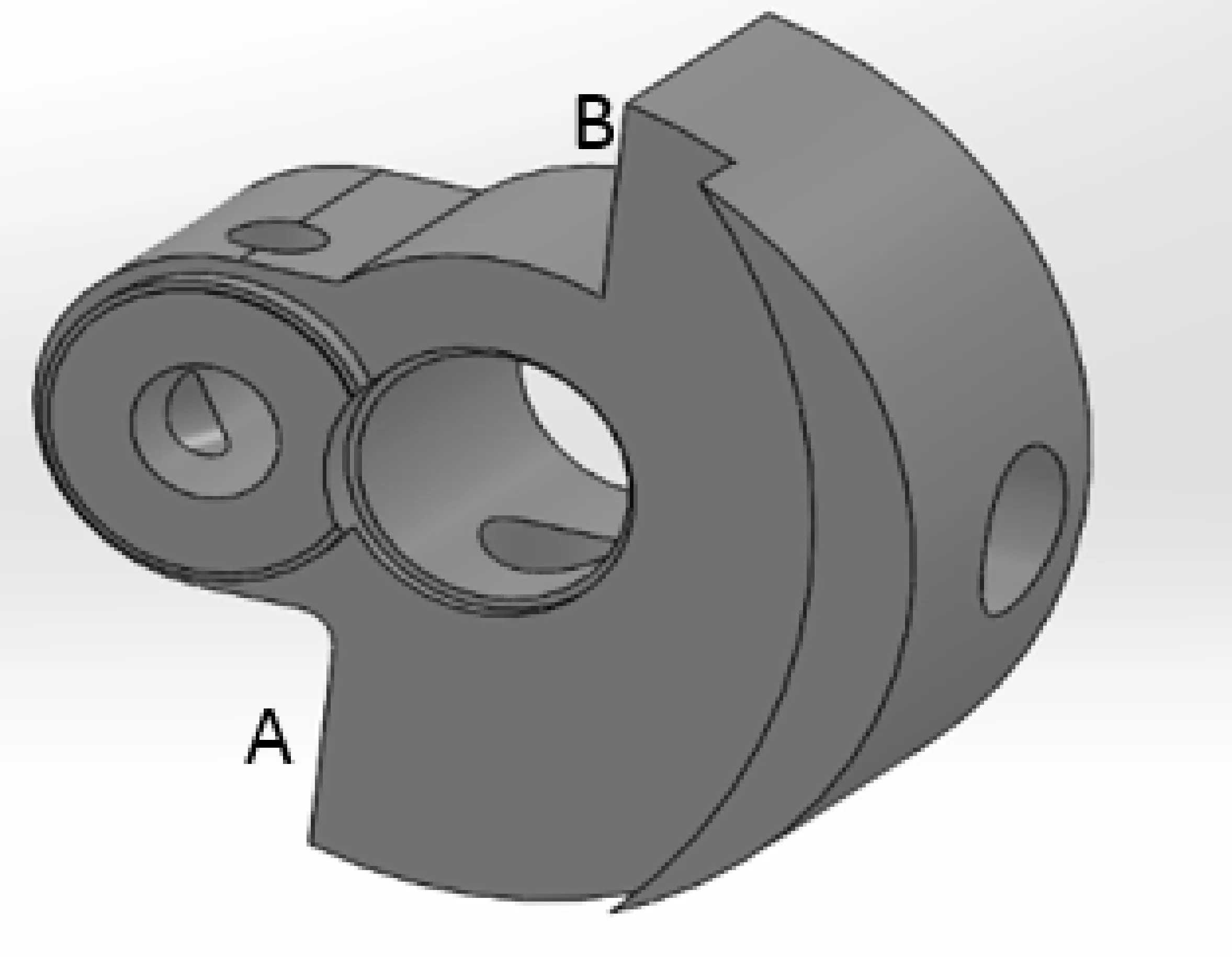
图7 优化后曲柄的三维模型图

代入构件1(摇杆)优化前后的各参数可得：

目 标:m1S1=-2.290×10-4-3.402 9×10-5i

优化前:m10S10=1.426 9×10-4-1.371 5×10-5i

优化后:m11S11=-2.187 5×10-4+3.112 8×10-5i

代入构件3(曲柄)优化前后的各参数可得：

目 标:m3S3=-6.026 8×10-4+1.684 0×10-5i

优化前:m30S30=9.693 1×10-4-2.188 0×10-4i

优化后:m31S31=-5.931 9×10-4+8.403 0×10-5i

将优化前后的结果与目标值做对比，结果显示优化后质径积更接近目标值，说明了零件结构优化的合理性.

4 刺布挑线机构的优化结果

对刺布挑线机构部分零件进行结构优化后，利用MATLAB编程得出优化前后的总质心轨迹对比图和总惯性力幅值对比图，分别如图8～9所示.

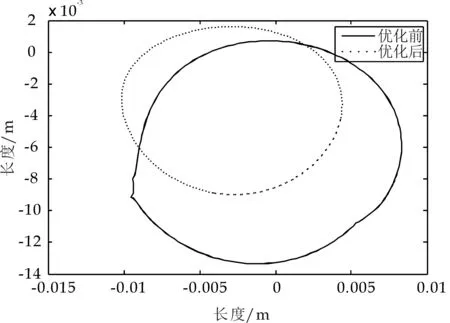
图8 刺布挑线机构优化前后总质心轨迹对比图

图9 刺布挑线机构优化前后总惯性力曲线对比图

由图8、图9可知，优化后机构总质心运动区域明显缩小，机构总惯性力最大值由1 300 N减小到900 N，降幅为30.77%；总惯性力变化幅值由1 200 N减小到850 N，降幅为29.17%.其总惯性力大小在整个周期的变化中降低了很多.无疑，本文通过对刺布挑线机构的平衡分析，进而在重要构件上进行的优化设计可一定程度地降低刺布挑线机构的振动，从而实现了降噪减振的目的，提高了运转平稳性，延长了机构的使用寿命.

5 结论

(1)采用复矢量法求解刺布挑线机构的总质心运动轨迹，该方法运算简便，有规律可循，不易出错，适用于通过计算机编程分析复杂的平面运动.

(2)基于平衡方法理论研究，建立机构总惯性力的平衡条件，采用部分平衡法能较好地解决如高速平缝机等复杂机械的动平衡问题，对抑制机器振动可起到较为明显的效果.

(3)结合最优化设计理论与MATLAB的数值分析法，对平缝机的重要机构进行平衡优化设计，可以获得较好的优化结果.同样的优化方法也可以应用于其它类似的机构.

[1] 郑子明,马晓建,国红波.包缝机曲轴平衡[J].轻工机械,2009,27(2)：31-35.

[2] 李时光.GC6150型工业缝纫机机壳动态特性及优化研究[D].西安:西安交通大学,2009：5-13.

[3] 何亚银，吴立言，李志锋,等.考虑转速影响的机构动平衡研究[J].机械设计,2008,25(3)：29-32.

[4] 张 侃，马晓建，张金柱.高速工业缝纫机动力学仿真与分析[J].轻工机械,2010，28(2)：17-21.

[5] 樊养余，尚永浩，赵文荣.缝纫机振动分析及整机平衡方法[J].机械设计,1997,14(7)：40-43.

[6] 王晓云.曲柄连杆机构动力学分析与设计系统研究[D].西安：西安建筑科技大学,2006：6-10.

[7] 陈立平,张云清,任卫群,等.机械系统动力学分析及ADMS应用教程[M].北京:清华大学出版社,2005.

[8] 常治斌，张京辉.机械原理[M].北京:北京大学出版社,2005:233-236.

[9] 刘亚辉，杨 华，周长江.平缝机刺布挑线机构的动力学优化[J].噪声与振动控制,2013(2)：91-94.

[10] 张 琳.用线性独立矢量分析连杆机构的平衡[J].机械设计与制造,2005(3)：14-15.

[11] 刘安心，杨廷力.平面连杆机构摆动力与摆动力矩优化平衡研究[J].机械科学与技术,1997，16(4)：647-651.

[12] 琚贻宏.平面七杆机构惯性力平衡分析的复矢量法[J].机械设计与制造,2004(5)：108-109.

[13] 王永泉，陈花玲，孙富贵.机构动态优化在工业缝纫机减振中的应用[J].机械科学与技术,2005，24(8)：947-968.

[14] 王学武，张 青，郭为忠.曲柄滑块机构惯性力优化平衡的新方法[J].机械科学与技术,2006，25(6)：687-688.

[15] 毕玉华，申立中，何自立.2102型农用柴油机平衡性分析及平衡性措施[J].昆明理工大学学报,2002，27(1)：86-88.

Balance analysis and optimization design of needle bar and thread take-up mechanism in industrial flat sewing machine

GUO Ying1, CAO Ju-jiang1*, ZHANG Ke-yu2

(1.College of Mechanical and Electrical Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China； 2.College of Science, Xi′an University of Architecture & Technology, Xi′an 710055, China)

With the development of science and technology，the high speed,efficient, precise and automation are becoming the trend of modern industrial sewing machine.In order to meet the requirements of the static and dynamic characteristics of internal structure,applying the complex vector method to derive the overall centroid trajectory equation and the total inertial force equation of the needle bar and thread take-up mechanism which generates the main vibration in high speed industrial sewing machine,optimizing the structure of parts through the balance analysis and using MATLAB for comparative analysis to prove the feasibility of optimization design.The optimization results show that the optimization method partly balances the strong inertia force which generates from the needle bar and thread take-up mechanism and effectively improve the dynamic performance of high speed industrial sewing machine in high speed operation.

high-speed industrial flat sewing machine； needle bar and thread take-up mechanism； balance analysis； structure optimization

2015-04-06

国家科技支撑计划项目(2013BAF04B01)

郭 莹(1991-)，女，陕西西安人，在读硕士研究生，研究方向：机械动力学及应用通讯作者:曹巨江(1955-)，男，陕西户县人，教授，博士生导师，研究方向：自动机械理论与设计方法、凸轮机构和先进制造技术，jjcao@sust.edu.cn

1000-5811(2015)03-0144-05

TH122

A