基于改进的快速Fermat数变换的卷积算法及其FPGA实现

周胜文， 周云生， 詹 磊， 董 晖

(北京遥测技术研究所北京100076)

引 言

卷积的快速实现是信号和图像处理中经常遇到的问题，在实践中，这些操作通常都采用快速傅里叶变换(FFT)算法实现，但在某些场合数论变换(NTT)要优于FFT。1971年Pollard［1］在有限群上定义了NTT，并给出了NTT变换对存在的条件。Mcclellan［2］于1976年提出了一种针对模运算的编码方式，从硬件角度分析了费尔马数论变换(FNT)的实现结构和流程，构建了一个64点16bit的FNT原型，并在此基础上探讨了长数据FNT的实现。Leibowitz［3］改进了Mcclellan的模运算编码方式，提出专门用于FNT的D1编码。从上世纪80年代起，我国学者也针对数论变换的应用展开研究。文献［4］分析了基4快速数论变换的FPGA实现，利用Xilinx Virtex2芯片实现了64点费尔马变换，但算法的运算时间太长。文献［5］讨论了基于蝶形运算的快速费尔马数论变换的FPGA实现，但是并未涉及FNT变换长度和位宽等关键问题。文献［6］研究了三个N点序列FNT合成一个2N点序列FNT的IP核实现方法，但该方法未能解决FNT变换长度增加与资源消耗急剧增大之间的矛盾。一直以来，人们不断研究通过类似Good-Thomas映射的多维分解技术解决FNT变换长度增加的问题，但是作大点数FNT时需要剔除模运算中的坏因子，伪费尔马变换(PFNT)能剔除坏因子却不利于模运算的FPGA实现。

本文从分析快速费尔马数论变换(FFNT)的基本蝶形算法出发，讨论了FFNT算法的应用局限及改进方法，之后提出了改进的FFNT(MFFNT)算法，将FFNT扩展到复数域来实现长复数序列的线性卷积。该MFFNT算法能与FPGA平台紧密结合，易于实际工程应用。

1 快速费尔马数变换(FFNT)

1971年，Pollard在有限群上定义了NTT变换对

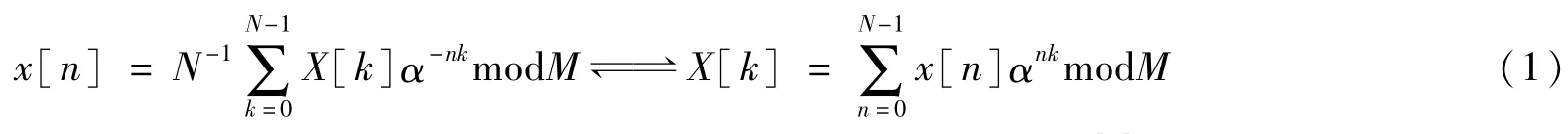
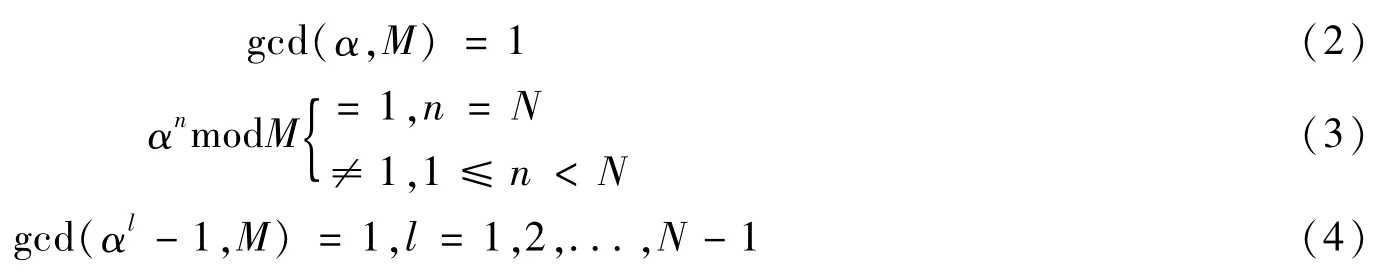
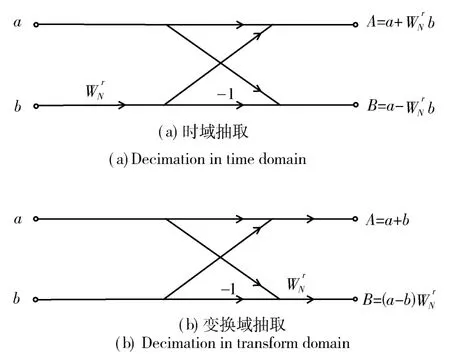
图1 FNT时域抽取和变换域抽取算法的蝶形单元Fig.1 Butterfly unit of FNT algorithm with the decimation in time domain and transform domain

其中，gcd(α，M)是α和M的最大公因数。当M为质数时，上面的所有条件均自动满足，模M=2b+1的NTT变换就称为费尔马数变换，特别是当b=2t时FNT存在快速算法。观察NTT变换对可以看出，不同于DFT变换，FNT变换为实变换，但FNT变换具有与DFT变换相似的周期性、循环卷积等特性。

因此，FNT算法可以通过基2时域抽取和变换域抽取的FFNT算法实现，如图1所示。与FFT算法相似，FFNT算法的基本单元是蝶形运算单元。

蝶形运算用D1编码系统实现只需要加法器和移位寄存器［8］，基于时域抽取的FFNT输入数据为逆序，输出为顺序，每个蝶形运算需要2个加法器、2个存储单元和1个运算周期。基于变换域抽取的FFNT输入数据为顺序，输出为逆序，每个蝶形运算需要2个加法器、3个存储单元和2个运算周期。可见，FFNT算法不需要乘法器，其运算时间大大缩减。

2 改进的快速费尔马数变换(MFFNT)算法

2.1 FFNT、PFNT、多维 FNT算法

如第1节所述，FFNT算法在运算时间、资源消耗上具有很多优点，但是实现长度N=2b=2t+1的FFNT算法的前提是模运算能够在硬件上快速实现，而满足如此特性的参数N和M并不多，更重要的是D1系统实现模运算的位宽W=b+1=2t+1，当变换长度增加时位宽会成比例增大，此时FNT算法在FPGA平台上实现时所需要的资源大大增加。

M非质数、变换长度N不是费尔马数的NTT称作伪变换［8］。对于伪费尔马数变换(PFNT)，首先根据变换长度N选取M，然后剔除M中的坏因子得到修正的M′，尽管PFNT算法的M′相比M小很多，但D1系统模运算的位宽仍很大，而且化简后的模M′≠2+1，难以在FPGA平台上实现。

因此，采用多维索引映射［9］，将长序列分解为二维或多维短序列，是增加FNT变换长度的一个有效方案。常用的多维映射变换有Cooley-Tukey变换、Good-Thomas变换及Agarwal-Burrus变换等，其基本原理是将总长度N=N1N2的变换分解为长度分别为N1和N2的两个短序列的变换。输入域的索引变换和输出域的索引变换分别如下

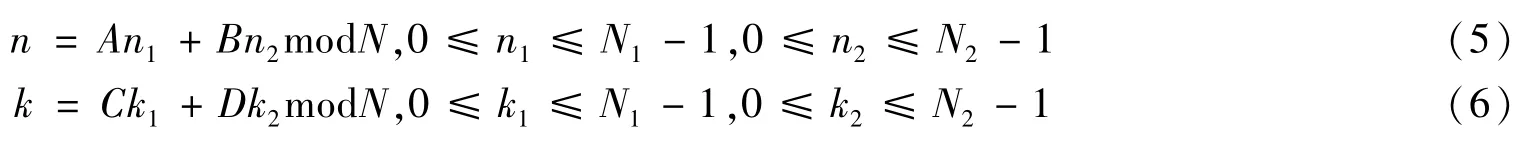
Cooley和Tukey提出的索引变换是最简单的映射，即令Cooley-Tukey变换的分解因子N1、N2可以是不互质的。Cooley-Tukey索引变换算法首先对输入序列进行索引变换，然后计算N2个N1点变换，变换结果乘以旋转因子后进行N1个N2点变换，最后对输出序列进行索引变换。

Good和Thomas提出的索引变换的最大特点是不需要乘以旋转因子，其代价是分解因子N1、N2必须是互质的，其中Good-Thomas索引变换算法与Cooley-Tukey索引变换算法类似，只是两次短序列变换运算之间不需要乘以旋转因子。

综上，采用多维索引映射虽然可以大大增加变换长度，但是必须要找到易于FPGA平台实现的FNT算法参数，由此可见将实数FFNT变换扩展到复数域是必然之举。

2.2 MFFNT算法

Dimitrov.V［10］在研究基3-FFT算法时提出了Eisenstein Residue Number System(ERNS)。ERNS是在闭集Z［μ］上定义的加法和乘法运算，其中

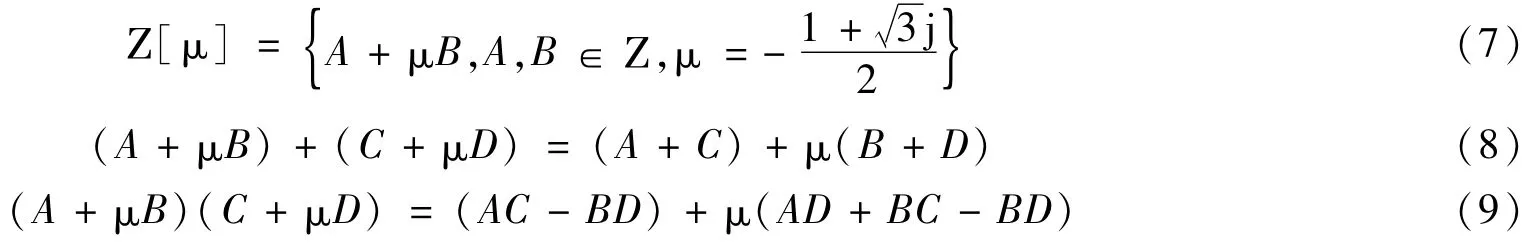
通过选取不同的FNT复数变换基α，可以大大增加定义在艾森斯坦余数系统上的FNT变换的有效长度。例如，当α=-2μ、M=2b+1时，式(1)拓展为ERNS域上的复数变换，变换长度扩展为N=6b，相比FFNT这一长度增加了3倍。因此，MFFNT算法将FFNT多维映射算法拓展到ERNS域，变换长度大大增加而实现变换所需要的位宽却不变，这非常有利于算法在FPGA平台上实现。另外，IMFFNT为MFFNT的逆变换，其变换过程与MFFNT算法相似，变换基为α的逆元即β=α-1modM，此处不再赘述。

MFFNT是在ERNS域的复变换，下面以变换基α=-2μ的96点复序列为例来阐述MFFNT算法的实现流程，具体的FPGA实现流程如图2所示。

①采用Good-Thomas变换将96点MFFNT分解为N1=3和N2=32的二维MFFNT，3个32点变换的变换基为-8，32个3点变换的变换基32点MFFNT变换为实变换，3点MFFNT变换为复变换。

②32点MFFNT变换按照Cooley-Tukey映射分解为L1=8、L2=4的二维变换，即4个8点MFFNT变换后乘以旋转因子再作8个4点MFFNT变换，乘以旋转因子矩阵通过移位寄存器实现，8点MFFNT变换可类似FFT由奇4点FFNT和偶4点FFNT合成。

③4点FFNT的计算分两个阶段，每个阶段按时域抽取算法进行两个蝶形单元的运算，每个蝶形单元的运算时间为一个时钟周期，资源消耗为4个加法器和4个存储单元。

2.3 ERNS复乘

MFFNT与FFNT的根本区别在于ERNS域复数的实部和虚部相比普通复数存在交织，ERNS域的复数乘法满足式(9)，如何在FPGA平台上用最少的乘法器资源实现ERNS域复数乘法是优化MFFNT卷积算法资源消耗的重要一环。如果采用实、虚部分别计算的方法，则需要4个加法器和4个乘法器。

Virtex6平台中的专用乘法器DSP48E1提供了强大的运算辅助功能，利用DSP48E1的预加器及级联端口，将式(9)改写为式(10)可知，任意两个复数的ERNS域乘法只需要3个DSP48E1就可以实现。

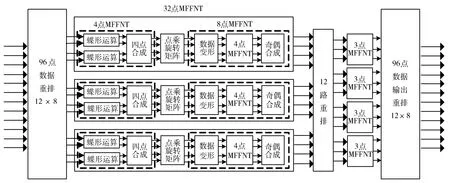
图2 96点MFFNT的FPGA实现流程Fig.2 Flow chart of ninety-six point MFFNT implemented on FPGA

而对于3点MFFNT中的复数乘法，由于变换基αpoint3组成的变换矩阵为

因此，3点MFFNT中的乘法同32点MFFNT中的蝶形单元相比运算时间更短，资源消耗更少，只需要两个寄存器和一个加法器。

另外，DSP48E1专用乘法器实现的是二进制补码的乘法运算，最终的运算结果还必须通过模化简转换成D1码，以方便进行IMFFNT运算。两个16位宽的数A、B相乘的结果可表示为高16位L和低16位S的组合，如式(12)所示，MFFNT的模运算在FPGA平台上用一个加法器就可以实现。

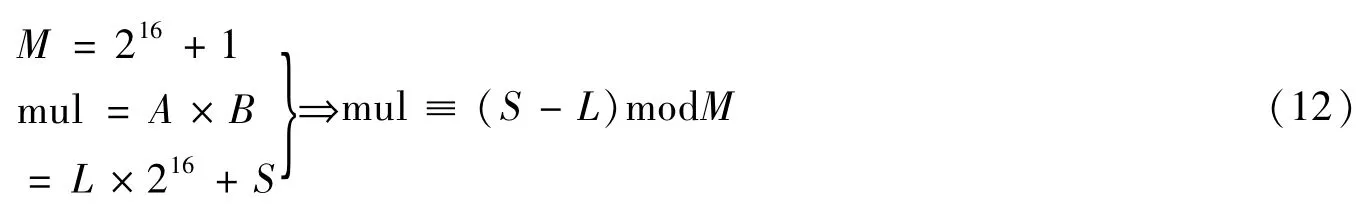
3 基于MFFNT的卷积算法

若x和y是模M定义的长度为N的序列，则x和y的循环卷积可以利用NTT来实现，令X、Y分别是x、y的NTT，则有

其中，Θ为ERNS域卷积。从式(13)可知，序列x和y的循环卷积可以通过两次NTT变换、一次N点复乘和一次NTT逆变换来实现，该特性与DFT类似，称为NTT的循环卷积特性。利用NTT实现循环卷积相比FFT实现卷积，其优势在于不需要消耗任何乘法器资源，并且运算时间可以大大减少。

MFFNT算法继承了FNT算法的优点，但是与FNT不同，MFFNT是ERNS域上的复数变换，因此基于MFFNT的ERNS卷积与圆周卷积是有区别的。

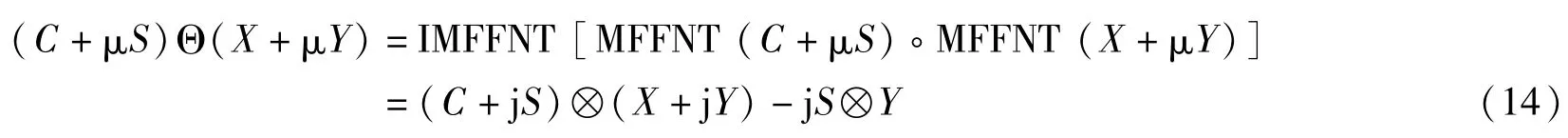
其中，⊗为圆周卷积，◦为ERNS域复乘。由式(14)可知，从ERNS域卷积变换到圆周卷积需要进行单位向量的变换，即对MFFNT的输入进行ERNS序列变换，对IMFFNT的输出进行IERNS序列变换，ERNS变换对如式(15)所示。

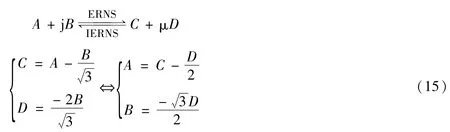
图3是基于MFFNT的卷积算法仿真结果。首先由Matlab分别生成32点和352点复随机序列，然后用ISE和Modelsim仿真软件读入相应的文本文档，之后将卷积算法的FPGA结果写到输出文件，最后通过Matlab软件读出卷积结果，并与理论值进行对比分析。从仿真对比图可以看出，基于MFFNT的卷积算法正确可行。

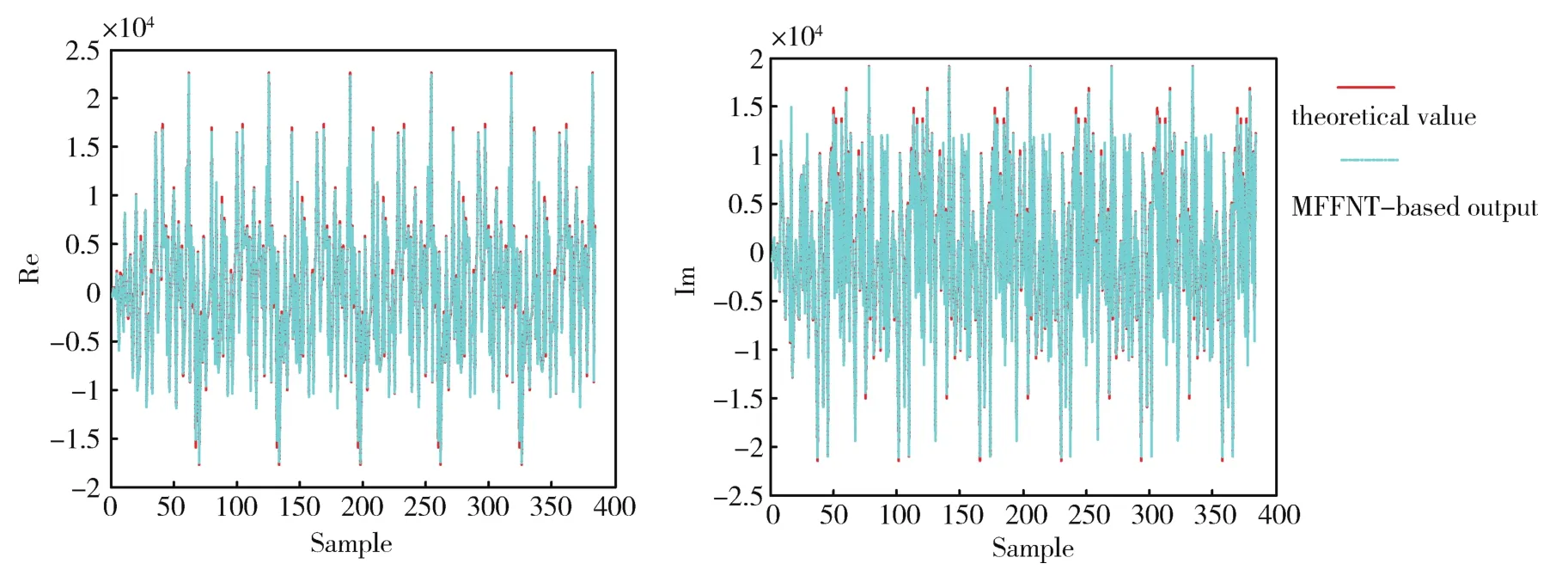
图3 基于MFFNT的卷积算法仿真结果Fig.3 Simulation results of the convolution algorithm based on MFFNT

图4是在Virtex6-LX240T平台上实现卷积时MFFNT算法和FFT算法的运算时间对比，图中左边基于MFFNT的卷积算法的运算时间为34个时钟周期，右边基于FFT的卷积算法的运算时间为40个时钟周期。可见，基于MFFNT的卷积算法相比基于FFT的卷积算法运算时间更少。

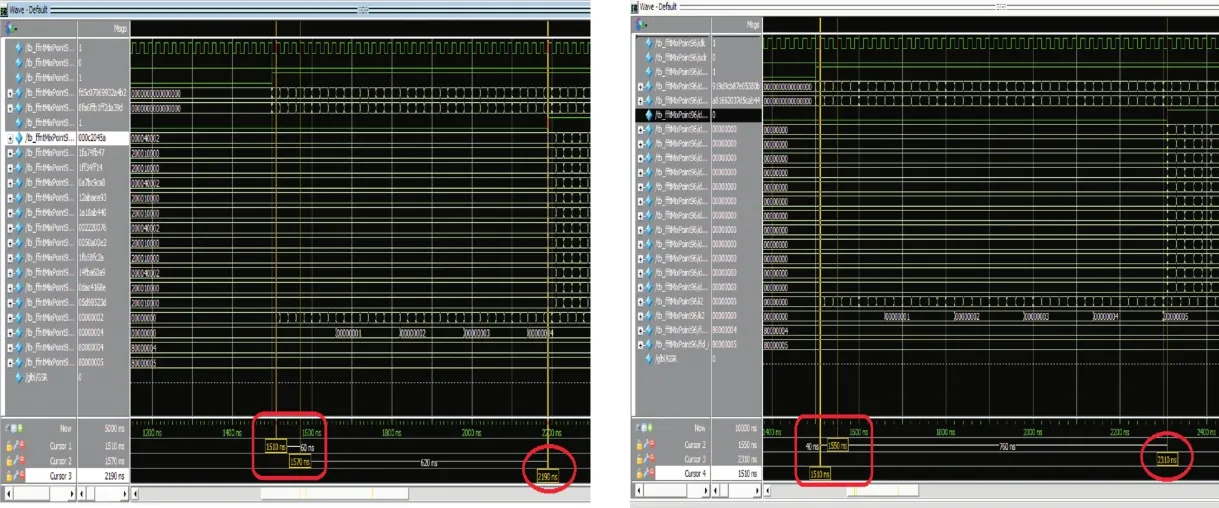
图4 基于MFFNT和FFT的卷积算法在Virtex6-LX240T平台上的运算时间对比Fig.4 Comparison of calculation time between the convolution algorithms based on MFFNT and FFT on the Virtex6-LX240T platform

图5是在Virtex6-LX240T平台上实现卷积时MFFNT算法和FFT算法的资源消耗对比，图中左边是基于MFFNT的卷积算法的资源消耗，右边是基于FFT的卷积算法的资源消耗。从图中可以看出，实现长复数序列卷积时，基于MFFNT的算法会消耗更多的逻辑资源LUT，但是比基于FFT的算法节约了约13%的专用乘法器DSP48E1，因此功耗相对较低。

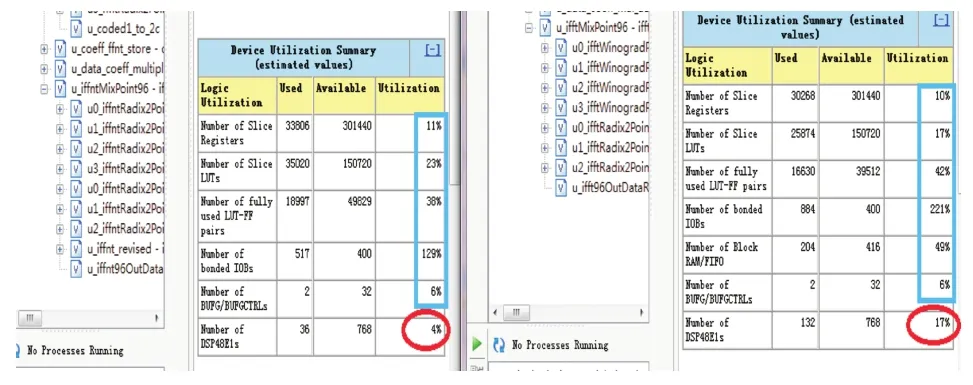
图5 基于MFFNT和FFT的卷积算法在Virtex6-LX240T平台上的资源消耗对比Fig.5 Comparison of resource consumption between the convolution algorithms based on MFFNT and FFT on the Virtex6-LX240T platform

4 结束语

本文从FFNT的周期性、对称性出发，对FFNT的蝶形运算结构进行分析，通过研究FFNT、PFNT及多维映射类FNT的优缺点，提出了一种复数域的MFFNT算法，并利用MATALB、ISE验证了Viretex6 FPGA平台上采用MFFNT算法实现线性卷积的可行性。仿真及应用结果表明，基于MFFNT的卷积算法相比基于FFT的卷积算法需要更少的乘法器资源，运算速度更快。

［1］Pollard J.The Fast Fourier Tranform in a Finite Field［J］.Mathmatics of Computation，1971，25:365 ～374.

［2］Mcclellan JH.Harware Realization of a Fermat Number Transform［J］.IEEE Trans.on ASSP，1976，24(3):216 ～226.

［3］Leibowitz LM.A Binary Arithmetic for the Fermat Number Transform［R］.Naval Research Laboratory Report，1976.

［4］陶 涛，初建朋，赖宗声，等.一种可参数化快速FNT的FPGA实现［J］.微电子学与计算机，2004，21(10):165～168.Tao Tao，Chu Jianpeng，Lai Zongsheng，etc.A Parameterized FPGA Realization of High-Speed FNT Processor［J］.Microelectronics & Computer，2004，21(10):165 ～168.

［5］余汉成，王成华，邵 杰，夏永君.基于FPGA的数论变换算法及应用的研究［J］.微计算机信息，2006，22(11-2):212～214.Yu Hancheng，Wang Chenghua，Shao Jie，Xia Yongjun.The Research into FPGA-based NTTAlgorithm and Application［J］.Microcomputer Information，2006，22(11-2):212 ～214.

［6］李新兵，初建朋，赖宗声，等.一种用FNT变换完成大点数循环卷积IP核的VLSI实现［J］.微电子学与计算机，2004，21(11):158～160.Li Xinbing，Chu Jianpeng，Lai Zongsheng，etc.A Parameterized FPGA Realization of High-Speed FNT Processor［J］.Microelectronics & Computer， 2004，21(11):158 ～160.

［7］Joseph H.Silverman 著.数论概述［M］.孙智伟，等，译.北京:机械工业出版社，2008，5.

［8］U.Meyer-Baese著.数字信号处理的FPGA实现 ［M］.刘 凌，译.北京:清华大学出版社，2012，4.

［9］Burrus C.Index Mappings for Multidimensional Formulation of the DFT and Convolution［J］.IEEE Transactions on Acoustic，Speech and Signal Processing， 1977，25，239 ～242.

［10］Dimitrov V，Jullien G A，MillerW C.Eisenstein Residue Number System with Applications to DSP［C］//Proceedings of the 40th Midwest Symposium on Circuits and Systems，1997，675 ～678.