还能往方程里面走走吗

李帮魁

一、天平模型强力支撑

在认识方程的教学过程中体现方程思想有两个问题需要关注：一是如何让学生依据等量关系写出等式，二是学生在写等式时怎样才能把未知量当作已知量。由于学生受到长达四年的小学算术思想影响，形成强烈的思维定势，因此很容易出现用算术方法求未知数解法。为解决学生这一认知矛盾与困难，吴老师以天平模型引领学生从直观上感悟等量关系，由此生成关系表达式，为建构方程的概念奠定厚实的背景经验。

【教学片段一】

教师出示天平图片：天平可以表示什么？（平衡、倾斜）

1.在天平两端都放50 g的砝码，能用式子表示吗？一端放50 g的砝码，另一端放30 g的砝码。

师：用式子表示，请写在纸条上。

生：50=50，30<50。

2.在天平一端放1根香蕉、一个30 g的砝码，另一端放50 g的砝码。

师：这时会出现什么情况？请用式子记录在纸条上。

学生写出：x+30=50，x+30>50，x+30<50。

3.在天平一端放1粒120 g的苹果、1根180 g的香蕉，另一端放300 g的砝码。

师：能用式子表示吗？

生：120+180=300。

4.在天平一端放1粒苹果、1根180 g的香蕉，另一端放300 g的砝码。

师：天平会怎样？

学生表示：180+x=300，180+x>300，180+x<300，180+□=300，180+苹果=300……

5.在天平一端放3粒苹果，另一端放300 g的砝码，天平平衡。

师：会记录下来吗？

学生记录：x+x+x=300，3x=300。

【赏析】吴老师在上述教学过程中五次以天平图和动作意象为载体，让学生展开观察与分析，要求学生只是描述数学问题事件，淡化学生求解未知量的意识，为未知量等同于已知量参与运算提供思维前提和条件。在此基础上引导学生用数学方式表达、记录这些表示关系的式子，为后续学习提供了丰富的研究素材。由于学生在天平模型支撑下对等量关系体验认识充分，为深刻理解“用未知数表达相等数量关系”这一方程本质积累了丰富的感性经验，为最终形成“方程是为了寻求未知数，在未知数和已知数之间建立起来的等式关系”的深刻认识积淀了厚实的经验基础。

二、完整经历建模过程

学生对于方程的认识过程就是一个数学建模的过程，如何让学生有效地建构这个数学模型？吴老师在这节课中让学生充分经历建模过程。在前面的观察、想象天平的活动中，学生感知了相等和不等量的关系现象，并引出了数量丰富的表达式，这是学生数学建模的开始。在大量积累方程背景知识的基础上，教者引导学生以分类的方式对天平不同情况的数学表达式进行分类，建构起清晰的方程模型。

【教学片段二】

师：我们刚才记录的时候有几种情况？分几类？

生：天平有平衡和倾斜两种情况，可以分两类。

师：挪动黑板上的纸条，分分类。

学生在黑板上挪动纸条。

等式：50=50，x+30=50，120+180=300，180+x=300，x+x+x=300，3x=300，180+□=300，180+苹果=300。

不等式：30<50，x+30>50，x+30<50，180+x>300，180+x<300。

师：你还可以把等式进一步分类吗？

学生独立思考后交流分类的方法。

含有未知数的：x+30=50，180+x=300，x+x+x=300，3x=300。

不含有未知数的：50=50，120+180=300。

学生没动180+□=300，180+苹果=300两个式子，吴老师把它们放在旁边。

引导学生圈出等式，再圈出和以往不一样的等式。

师（手指着含有未知数的等式）：这些等式叫作方程。大家说一说，什么是方程，对方程有什么感觉？

生：一个未知数，一个已知数，相加等于一个数，

是方程。

师：只能相加吗？

生：加、减、乘、除都可以。

生：180+□=300，180+苹果=300是方程吗？

生：应该是，因为“□”和“苹果”都是不知道的未知数。

【赏析】上述教学过程中，学生经历了两次分类：第一次分为等式和不等式；第二次把等式分为含有未知数和不含有未知数的，从而得出方程概念的意义。这一环节与“片段一”融合为一体，加上课尾现实情境中用方程解决问题的环节，完整地呈现出了“问题情境—建立模型—求解验证”的数学建模的全部过程，有利于学生在这个过程中理解、感悟模型思想的本质，更有利于促进学生从数学的视角去发现、提出、分析与解决问题，培养创新意识。

三、多走一步深度感悟

当学生以天平模型为载体完整经历了数学建模过程，得出了方程概念后，吴老师没有提及和强调教材中“含有未知数的等式叫作方程”的描述性定义，而是引导学生在“运用与解释”中逐步窥视方程的本质内涵。

【教学片段三】

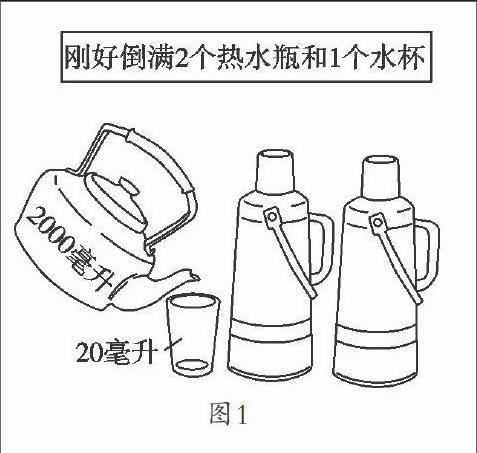
1.课件出示情境图片（图1），并附有文字说明。

师：请大家唤起心中的天平，用式子表达出来。

生：2x+20=2000。

生：（2000-20）÷2。

师：哪个是方程？

生：2x+20=2000。

师：（2000-20）÷2是你们熟悉的，它与2x+20=2000有什么不同？

生：方程是把不知道的和知道的，通过天平表达出来。（2000-20）÷2是从知道的一步一步求出不知道的。endprint

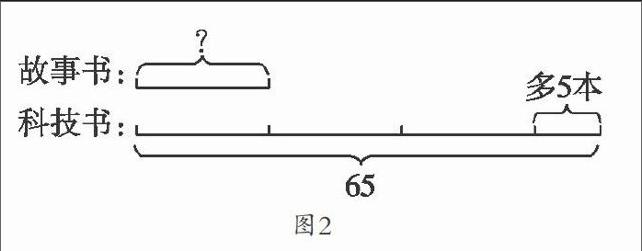
2.教师出示图2。

师：能求什么呢？请写下来。

生：①3x+5=65，②（65-5）÷3，③（65-5）÷3=x。

师：哪些是方程？

生：①和③。

生：③还是以前的思路。

师：方程和以前的有什么不一样吗？

生：方程有未知数。

师：只是未知数吗？还能往里边走一走吗？

生：以前是从已知数求出未知数，方程是把不知道的和知道的一起变成等式。

教师随手在黑板上画一条河：就好像有一条小河，我们站在河的这边，对岸有一颗宝石，我们要怎样拿到对岸的宝石？

生：从岸边出发，摸着石头一步一步地走到对岸拿到宝石。

师：这就好比以前的数学方法，从已经知道的一步一步地去拿到宝石。还有其他方法吗？

生：用绳子拴住拉过来。

师：用一根绳子拴住对岸的宝石，然后顺着绳子拿到宝石。就好像方程一样，把不知道的和知道的建立等式关系，写出方程，再求出未知数。两者目标一样，思考方式不一样。

生：相等的关系就是绳子……

【赏析】吴老师所采取方法充分暴露了学生的认知，先是在异同比较上凸显方程的本质，当学生在“水壶倒水”的问题中出现“2x+20=200，（200-20）÷2”两种不同思维的式子，以及在图2的表达中出现“3x+5=65，（65-5）÷3，（65-5）÷3=x”三个不同表达式时，在结合具体事例背景的对比中，使学生生成“以前是从已知数求出未知数，方程是把不知道的和知道的一起变成等式”的认知。其次是以事例类比促领悟，当学生在上述比较中对方程的本质内涵有理解但又无法表达时，吴老师及时以“拿到河对岸的宝石”的事例进行类比，通过对取宝石不同途径的分析，让学生进一步感悟“两者目标一样，思考方式不一样”。体现了“方程是为了寻求未知数，在未知数和已知数之间建立起来的等式关系”与“方程概念的核心是要‘求未知数”的本质内涵。

“还能往方程里面走走吗？”这句话是吴正宪老师在执教“认识方程”一课时，在课前与课中对听课教师和学生提出的思考。大师智慧的课堂教学实践告诉我们，教师和学生都可以向方程本质内涵里面走一走，多走一步便能为学生多开一扇窗，学生由此可以看到更多的风景。正如吴正宪老师所说：“有时候在课堂上‘多喘半口气儿，多走一步就有可能触摸到数学的本质。”

（作者单位：重庆市沙坪坝区教师进修学院 责任编辑：王彬）endprint