含隧洞场地条件结构TMD控制研究

2015-04-29周占学胡鸿亮

河北建筑工程学院学报 2015年3期

关键词：最优控制隧洞加速度

周占学胡鸿亮

（河北建筑工程学院，河北张家口075000）

0 引言

地铁、隧道等地下结构对地上建筑抗震的影响已成为城市防灾减灾研究中的一个重要话题.因此，对含隧洞场地条件结构振动控制的研究具有重要的意义.

通过对包括地下隧洞的高层结构体系的有限元分析，研究隧洞对结构自振频率的影响，比较有无TMD时结构的动力反应，为含隧洞场地条件结构的振动控制提供参考.

1 受被动控制的结构的运动方程

被动控制由于其设备相对简单，造价相对低廉，易于维修和保养等特点，是目前应用最为广泛的结构控制方法，其中TMD是一种经典的动力吸振装置.设计TMD控制的第一步是设计出阻尼器的参数，目前比较流行的参数设计法是准最优控制法.准最优算法是指根据最优控制原理，来设计被动控制系统的参数，从而使结构的动力响应接近在最优控制下的结构动力响应.根据瞬时最优算法计算出结构的最优控制力之后，就可以设计控制系统中TMD的参数.

准最优控制方法有很多，有Kosut提出的最小误差激励法和最小范数法，以及由下乡太郎提出的等效最优控制特性法等，这里采用的是等效最优控制特性法.此法假设控制装置是由弹簧和阻尼器所组成的，计算出最优反馈控制时的最优弹簧控制力和阻尼控制力的方差，以及最优反馈控制时控制装置所在位置的结构位移和速度反应的方差，进而计算控制装置的准最优参数.

第i个TMD与结构反应状态向量之间的关系是：

式中，｛ν｝i是TMD的位移向量，｛X｝是结构的状态向量是结构上第i个TMD参数与结构反应状态向量｛X｝的关系矩阵.若使结构在TMD处的最优反馈控制反应与被动控制的反应相等，则第i个TMD的位移、速度方差应为：

第i个最优控制力可以分解为：

因此，取第i个TMD的控制力与最优反馈控制力相等，可以得到TMD弹簧力和阻尼力的方差为：

由此可以得到第i个准最优刚度参数和阻尼参数

有了各个TMD的参数之后，就可以利用时程分析法来分析结构在被动TMD控制之下的动力响应了，公式推导过程如下：

结构的运动方程

其中

TMD的运动方程是

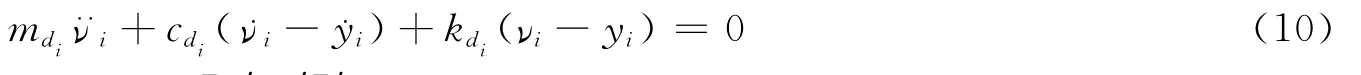
把以上两式写成矩阵形式，并令｛z｝＝［y′，ν′］′，有

其中［E］是控制装置矩阵，与主动控制中的装置矩阵相同.

另外在设计TMD控制时，TMD的参数是根据瞬时最优算法来设计的，但是由于实际结构的限制，TMD的参数要进行一定的调整，把TMD的振动频率调整到其所控制的振型所对应的频率上，否则TMD会达不到设计的控制效果.

表1 TMD参数表

2 自由场反应研究

自由场反应就是场地上没有任何结构、场地平整时的场地的时程反应，自由场反应是研究各种场地条件下结构反应的基础.

2.1 自由场反应有限元模型

场地长度为150m，深度为30m，为均匀场地，弹性模量为40×108MPa，泊松比为0.3，密度为2049kg／m3.自由场反应有限元模型如图1所示，据此进行有限元计算分析.

图1 自由场有限元模型

2.2 自由场振型分析

自由场振型经计算，其各阶频率结果如表2所示.

表2 各阶频率

2.3 自由场分析

输入的地震波为El Centro波南北向，为便于比较，将El Centro波加速度峰值调整到0.1g，如图2所示.

图2 EI－Centro波峰值调整至0.1g

自由场位移、速度和加速度反应结果分别如图3、图4和图5所示.

图3 自由场水平位移时程曲线

图4 自由场水平速度时程曲线

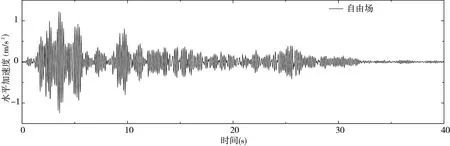
图5 自由场水平加速度时程曲线

水平位移最大值为0.001m，对应时间为3.56s，水平速度最大值为0.033m／s，对应时间为3.6s，水平加速度最大值为1.25m／s2，对应时间为3.56s.可见，水平加速度大约放大了25%.

3 含隧洞场地结构的自振频率

3.1 模型

分析场地长度为150m，深度为30m，为均匀场地，弹性模量为40×108Pa，泊松比为0.3，密度为2049kg／m3.地面结构为平面框架，每跨为10m，地下2层，地上为10层，层高均为3m.框架材料密度为2500kg／m3，松比为0.2，弹性模量为4.83×1010Pa.隧洞直径为10m，位于场地土中间部位，结构体系的模型如图6所示.

图6 含隧道结构体系

3.2 结构自振频率

隧洞位于场地中心，其位置位于建筑结构正下方.以无隧洞结构体系为工况1，有隧洞结构体系（图6所示）为工况2，分别计算两种工况下结构体系各阶振型频率，计算结果如下：

表3 各阶振型频率

图7 隧洞变动时结构体系各阶频率

可见，隧洞位置位于结构体系正下方时，与无隧洞情况相比，结构自振频率下降达70%.

4 隧洞－结构体系结构控制研究

在结构顶部安装一TMD控制器（如图8所示），对结构体系进行被动控制.按照结构体系的自振频率、质量计算出TMD的最优参数并进行控制计算.仅对地下隧洞位于结构正下方时进行计算，计算结果如下：

图8 TMD控制系统示意图

图9 有控、无控结构位移数值

图10 有控、无控结构速度数值

图11 有控、无控结构加速度数值

图12 有控、无控结构弯矩数值

图13 有控、无控结构剪力数值

图14有控、无控结构轴力数值

图9－14分别为有控及无控情况下，结构体系的加速度、速度、位移、弯矩、剪力及轴力的数值比较.可见TMD在根据隧洞－结构体系优化参数的情况下，对结构反应的控制效果很明显，各楼层的位移除负层外其他楼层可降低22%～57%，速度除3层和4层略有增加外其余层可降低3%～16%，加速度至少降低22%，弯矩和剪力至少降低了60%以上，轴力则降低了50%左右.