ATIS环境下的多用户多准则交通均衡模型分析

吴鹏昆,吴园园,徐 兵

1) 南昌大学管理学院,南昌 330031；2) 南昌大学经济管理学院,南昌 330031

【交通物流 / Transportation Logistics】

ATIS环境下的多用户多准则交通均衡模型分析

吴鹏昆1,吴园园2,徐 兵1

1) 南昌大学管理学院,南昌 330031；2) 南昌大学经济管理学院,南昌 330031

为分析先进出行者信息系统(advanced traveler information system，ATIS)对交通均衡的影响，建立一个考虑多用户多准则的交通均衡模型. 在模型中，根据ATIS市场占有率和用户收入水平差异将出行者分为4类，对每一类出行者，基于出行时间和出行费用线性组合的出行成本，根据Logit模型进行路径选择. 以中国深圳市梅林关的一个起讫点(origin-destination，OD)进行实证分析，发现市民出行成本与路段拥堵系数不能同时降低. 在现今经济水平下，ATIS可减少人们平均出行成本. 随着经济水平的提升，人们才会慢慢利用ATIS选择可以减少平均拥堵系数的路径. 最后，对模型参数进行了灵敏度分析.

智能交通；先进出行者信息系统；多用户多准则；交通均衡；Logit随机均衡；起讫点矩阵

随着经济的发展，交通供给与需求间矛盾越来越明显，交通拥堵现象日益成为阻碍城市发展的重要因素. 为确切描述并解决交通问题，Wardrop[1]提出了确定性交通均衡原理，包括用户均衡原理和系统最优原理. 确定性交通均衡原理假设出行者完全理性，且完全掌握交通状况与信息，这与实际不符. 于是，有学者提出了以效用理论和极值理论为基础的随机交通均衡理论[2-3].

在随机交通均衡理论中，市民通过对出行时间、费用和安全性等多准则进行评价，选择出行路径. 选择理论主要包括：① 假设误差项相互独立且服从相同分布，以得到结构简单且可解释性强的Logit模型[4]；② 假设误差项非独立，且联合分布服从多变量正态分布，以得到复杂的随机概率模型[5-6]. 考虑到收入、年龄和出行目的等差异，出行者对影响出行选择偏好不同，需要将出行者分类考虑．因此，现今学者开始研究多用户、多准则的随机均衡模型[7-9]，以便最客观地刻画实际的交通路网．

黄海军等[10]指出，公路网络的利用效率不高，路程的6%和时间的12%被浪费了，驾车者平均多行驶了6%的距离. 交通信息系统可以给驾车者带来9%～14%的利益[11]，使公路网络进入最佳状态，产生4%的净收益[12]．于是，学者愈发重视交通信息，特别是研究智能交通系统对交通均衡的影响．赵丹[13]就交通信息对出行者的路径选择进行了较全面剖析．赖信君等[14-15]也研究了交通信息发布对城市路网的影响，简单地考虑了交通信息对出行者路径的影响，并将交通路网进行了较大简化．郭仁拥等[16]虽然基于先进出行者信息系统(advanced traveler information system，ATIS)对复杂的多用户、多准则随机交通均衡进行了演化，但没有给出演化的直观结果和实例．

目前的研究已准确构建了多用户多准则交通均衡模型，但缺少实证分析，更鲜有对模型中参数的灵敏度分析．本研究通过Logit模型研究多用户、多准则随机交通均衡模型在ATIS环境下的演化，选取较为拥堵的深圳市梅林关进行实证研究，分析ATIS的使用率，探究ATIS对交通均衡的影响，并对模型参数进行了较详细的灵敏度分析．

1 模型的建立

1.1 随机均衡交通模型

用有向图G=(N，A)表示交通网络. 其中，N是节点(路口)集合；A是有向边(道路)集合. 交通网络中有M类出行者，依据K个准则选择路径.

对起讫点(origin-destination，OD)w，令

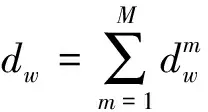
(1)

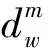
所有可行流量均满足流量守恒条件(2)和非负约束条件(3)，且路径流量与路段流量满足式(4).

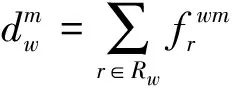
(2)

frwm≥0, ∀r∈Rw,w∈W

(3)

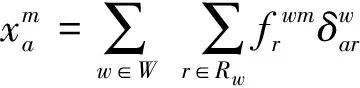
(4)

其中，W为OD对的集合；

出行者出行会涉及成本计算问题. 令

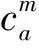
(5)

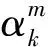
第m类出行者通过路径r∈Rw的广义成本为

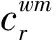
(6)

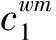
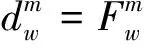
(7)

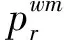
(8)

假设影响第m类出行者选择路径的随机变量均服从期望值为0、方差与θm2成反比的相互独立的Gumbel分布，则期望最小出行成本为

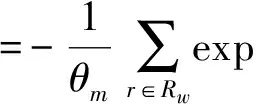
(9)

其中，θm为感知误差，其值为大于0的常数．

基于Logit的路径选择模型为

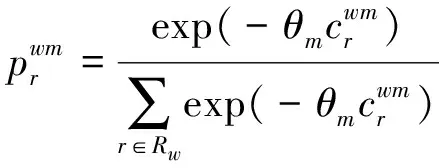
(10)

1.2 多用户多准则的确定

出行者可分为使用和不使用ATIS两组．两组都随机选择出行路径，使用ATIS的对道路阻抗的感知误差比不使用ATIS的小．每一组中的高收入人群更在意时间；低收入则更在意费用. 所以，又将每组再分为高收入和低收入两类．于是，出行者被分为4类：使用ATIS的高收入出行者；使用ATIS的低收入出行者；不使用ATIS的高收入出行者；不使用ATIS的低收入出行者.

影响出行者进行路径选择的因素非常多，如时间、费用和路段拥堵系数等．这些影响因素之间大多自相关，且影响程度有很大区别，其中，时间和费用相对重要且相关性较低. 所以，在此将准则定为出行时间和费用两部分.

1.3 Logit路径选择模型

计算出行时间ta，通常采用美国公路局的路段阻抗函数(U.S.bureauofpublicroads，BPR模型)及参数[17]，其表达式为

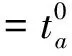
(11)

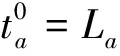
(12)

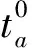
计算出行费用借鉴黄海军等[10]在研究中采用的方法．设网络中有R条平行路径，路段a的费用为

ga(x)=ρaxa+ba

(13)

其中，ρa为路径a的拥堵系数，且ρa=xa/ua；ba为路径a的自由行使费用，且

ba=LaNa

(14)

其中，Na为路段a自由行使时的单位费用.

类似文献[16]，将实际出行成本定义为行使时间和行使费用的线性组合[16]，即将式(5)转换得到第m类出行者在路段a的出行成本为

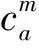
(15)

其中，λm表示第m类出行者的时间价值，将费用转换为等价的时间. 显然，不同出行者的λm会不一样.

将式(15)结合式(6)并代入式(10)，可得到不发布信息时的Logit模型为

(16)

分析发现，式(16)展开后参数仅剩下θm和λm两类，4类出行者合计8个参数．θm与出行者是否使用ATIS有关．较大的θm值意味着较小的感知误差，使用ATIS的出行者的θm值会比不使用ATIS的θm值大．λm指时间价值，其值显然与出行者的收入有关．高收入出行者更在乎时间，所以λ较大．通过这两类参数可分析前文确定的4类出行者．接下来讨论如何通过参数对均衡情况进行分析．

2 实证分析

2.1 问题描述

由于历史原因，深圳由原关内和关外两个区域组成. 原关内和关外由自然山丘隔开. 相当一部分人在关外居住，但在关内上班，导致上下班高峰期各关口成为交通最拥堵的地方，尤以原布吉关和梅林关为甚.

选取梅林关一对较为重要且拥堵的OD对进行分析. 通过梅林关进关日均车流量为81 529pcu[18]，通过该OD对的日均车流量有30 000pcu，早高峰时期通过该OD对的至少有6 000pcu. 该OD对包含14条路段，GoogleEarth标识如图1.

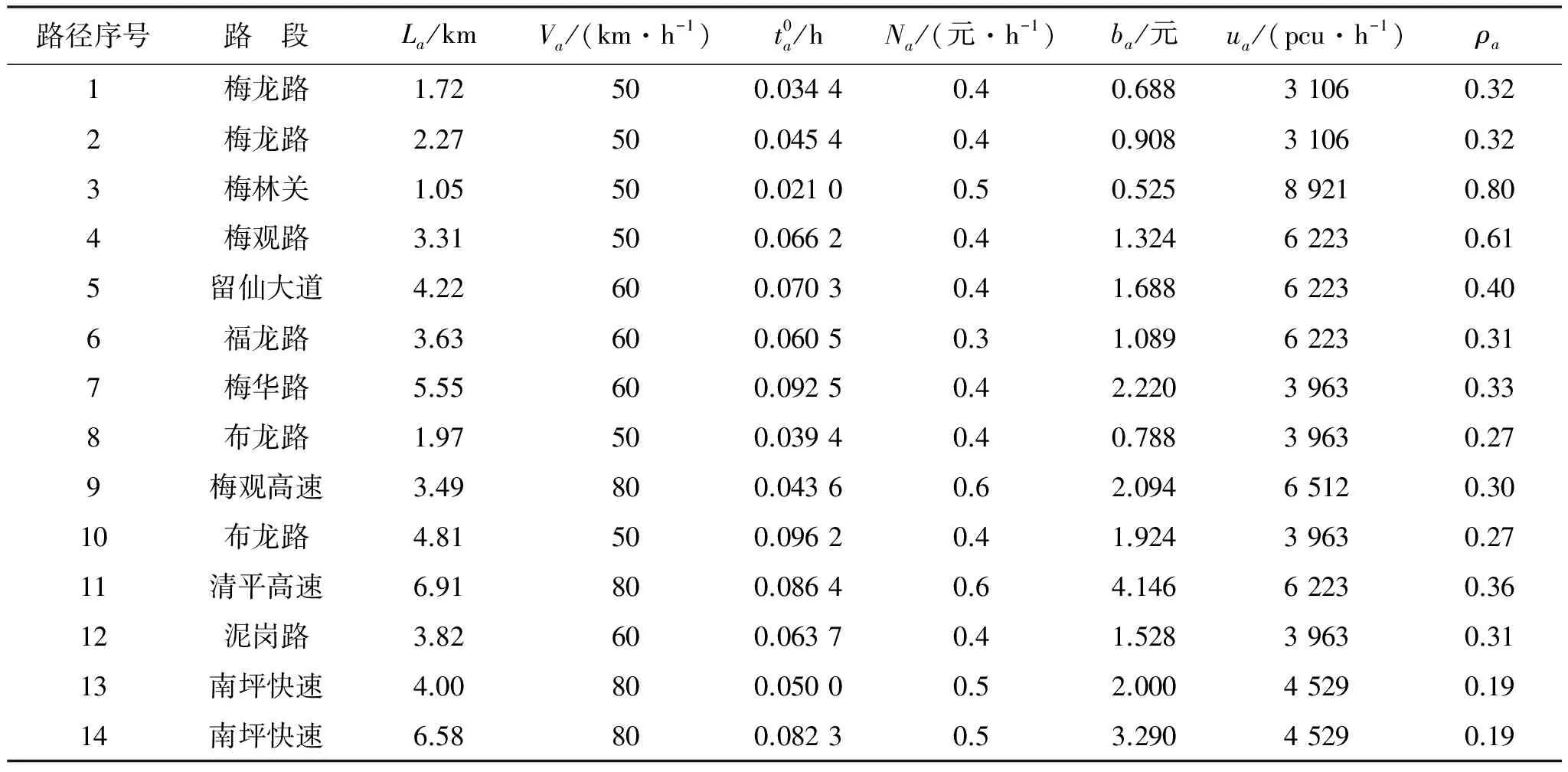
对14条路段的信息进行查找并处理，按照式(12)和(14)处理，得路段信息如表1[19].

该OD对中的14条路段可以组成6条有效路径，供出行者选择，使用GoogleEarth将这6条路径标识，如图2．路径1～6依次包含路段(1→2→3→4)、(1→5→6→7)、(8→10→11→12)、(1→5→13→4)、(8→10→14→4)和(8→9→3→4)．

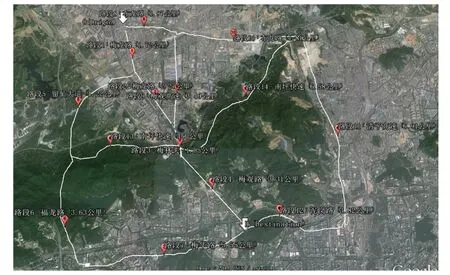
图1 选取OD对间的14条路段Fig.1 (Color online) Fourteen roads between OD pairs

表1 选取OD对间的14条路段的当前信息

Table 1 Current information of fourteen roads between OD pairs

路径序号路 段La/kmVa/(km·h-1)t0a/hNa/(元·h-1)ba/元ua/(pcu·h-1)ρa1梅龙路1．72500．03440．40．68831060．322梅龙路2．27500．04540．40．90831060．323梅林关1．05500．02100．50．52589210．804梅观路3．31500．06620．41．32462230．615留仙大道4．22600．07030．41．68862230．406福龙路3．63600．06050．31．08962230．317梅华路5．55600．09250．42．22039630．338布龙路1．97500．03940．40．78839630．279梅观高速3．49800．04360．62．09465120．3010布龙路4．81500．09620．41．92439630．2711清平高速6．91800．08640．64．14662230．3612泥岗路3．82600．06370．41．52839630．3113南坪快速4．00800．05000．52．00045290．1914南坪快速6．58800．08230．53．29045290．19

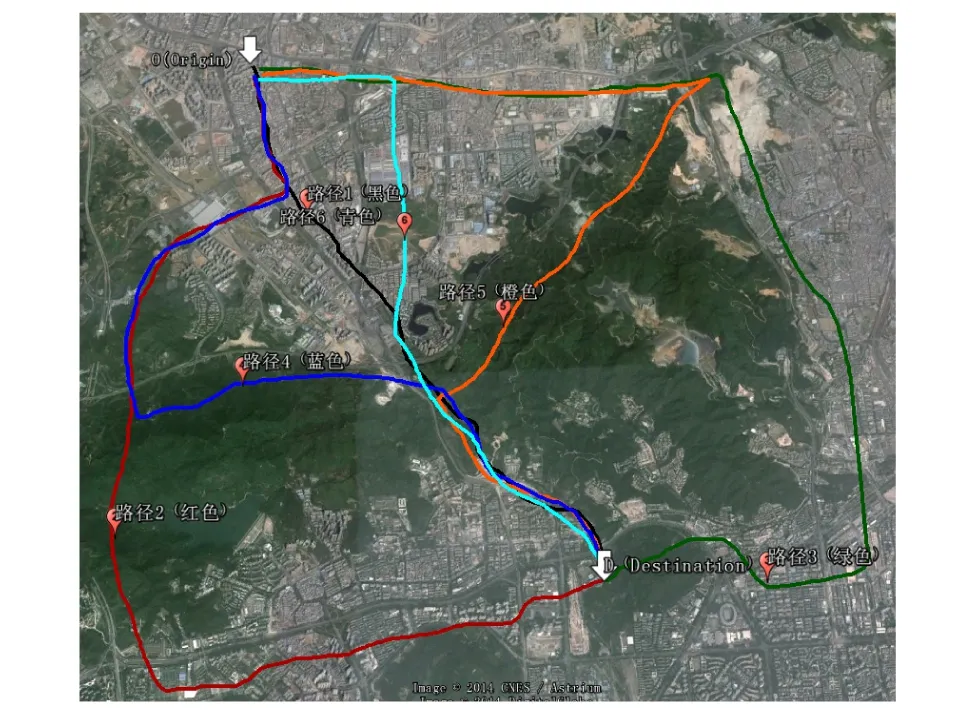
图2 选取OD对间的6条路径Fig.2 (Color online) Six paths between OD pairs

2.2 算法描述

对本研究所示路网，出行时间和出行费用两个准则都是交通流量的函数，可采用逐次平均法(method of successive average，MSA)求均衡解．MSA是模拟驾驶者对道路网络不断学习来寻求均衡解，直到两次解之间的区别小于收敛值ηsld，从而近似得到均衡解. 具体步骤为：

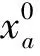
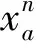
5)收敛性检查．当前后两次迭代满足收敛性要求，即满足式(17)，则计算停止；否则，返回步骤2)．

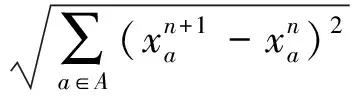
(17)

2.3 均衡解的求取与分析

已知OD对的基本情况后，接下来确定Logit模型的参数θm和λm. 借鉴文献[16]，出行者的参数θm值为[0.5，0.1]，低收入和高收入的时间价值λm为[20，35]．本研究设低收入和高收入出行者的时间价值分别为λ1和λ2. 综合中国现状和研究[14]，得到4类用户的比例，如表2．

表2 四类出行者所占比例

Table 2 Proportion of four types of travelers 单位： %

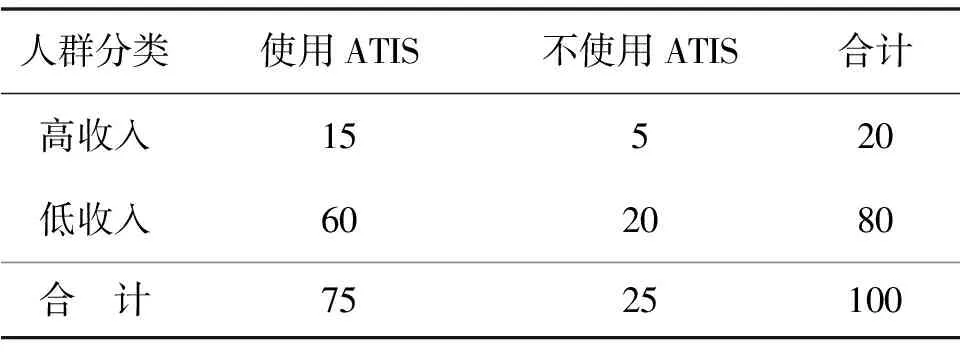
人群分类使用ATIS不使用ATIS合计高收入15520低收入602080合 计7525100

利用Matlab编程软件计算，得到图3. 发现优化前出行者需花费出行时间成本(含转换后的出行费用)为0.719 2 h，交通均衡后的出行时间成本为0.668 8 h. 此时，各路段的平均拥堵系数由0.370 9减到0.367 1，交通均衡还可以很好权衡各个路段，如原先拥堵系数为1.287 8的路段1属极度拥堵，优化后可以使其减少到0.979 8，路段2的拥堵系数甚至由0.965 9减少到0.332 0.

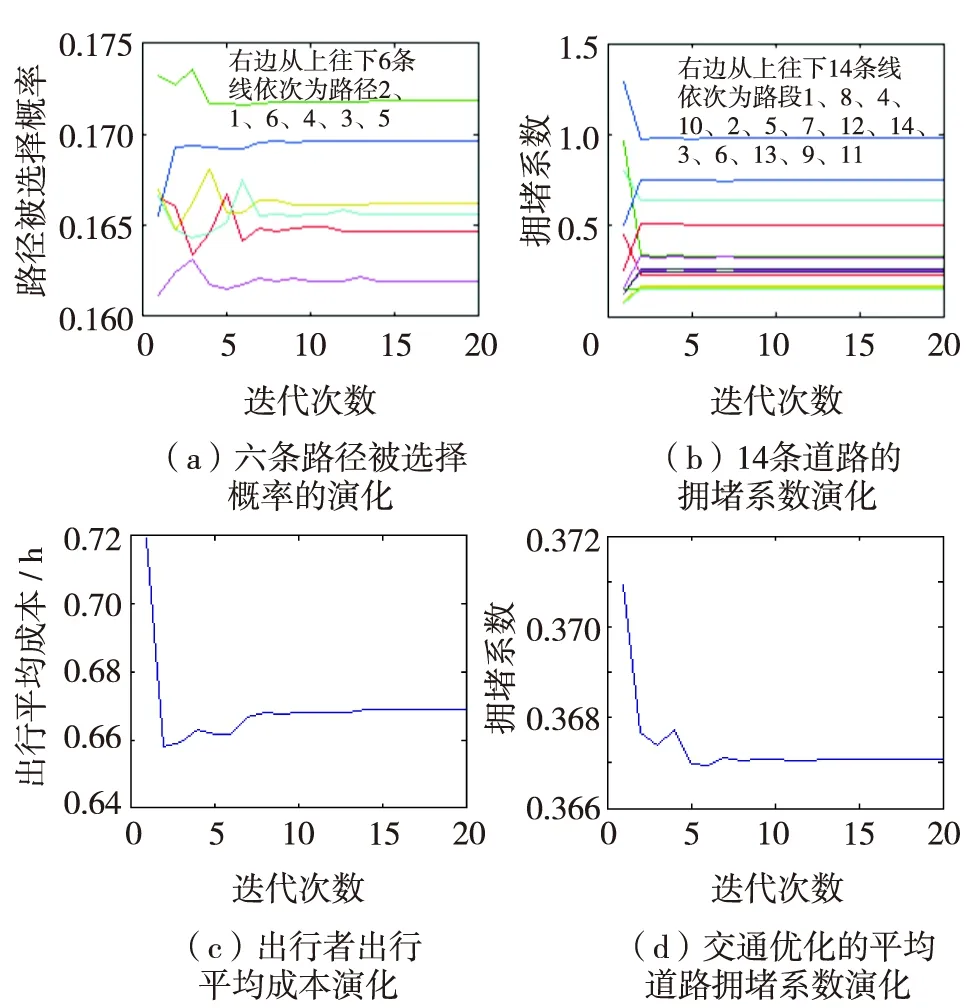
图3 交通优化演化图Fig.3 (Color online) Evolution figures for the traffic optimization

从图3还可见，交通均衡时的出行成本并非最优. 最少的出行成本为0.658 1 h，对应的平均拥堵系数为0.367 7，大于交通均衡时的0.367 1. 表明拥堵系数与出行成本有矛盾，不能同时达到最优.

3 ATIS使用率分析

为进一步探索ATIS使用率对交通均衡的影响，改动第2章所用的ATIS使用率，比较不同ATIS使用率下的均衡解. 本研究设ATIS的使用率取值范围为0～100%，并以5%为变动量.

3.1 参数不变的ATIS使用率分析

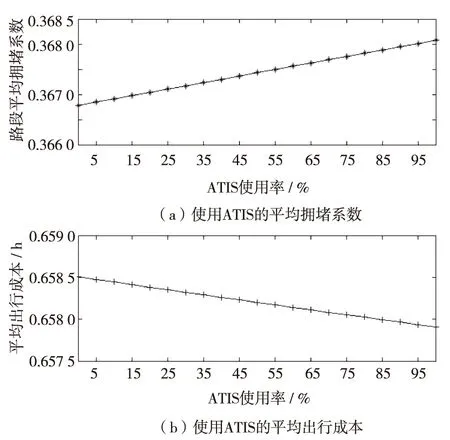
图4 固定参数的ATIS使用率的影响分析Fig.4 Analysis of ATIS usage rate with fixed parameters

固定第2章所用参数(θm，λm)和高收入比例(20%)的取值. 利用Matlab编程软件计算得到图4. 由图4可见，随着ATIS使用率的提高，路段平均拥堵系数越来越高，但驾驶者的平均出行成本越来越低. 当没有驾驶者使用ATIS时，平均拥堵系数为0.366 8，平均出行成本为0.658 5h；当所有驾驶者都使用ATIS时，路段的平均拥堵系数为0.368 1，平均出行成本为0.657 9h. 可见，ATIS对交通均衡确实有影响．但由于出行成本和拥堵系数存在矛盾，现在驾驶者出行更看重出行成本，使得在现阶段，使用ATIS反而会加大交通拥堵.

3.2 参数可变的ATIS使用率分析

设所用参数(θm，λm)和高收入比例(20%)可变. 当感知误差θm可变时，ATIS对交通均衡的影响见图5. 分析图5可得，若使用与不使用ATIS的感知误差一样时，ATIS的使用率对交通均衡没有任何影响；若使用与不使用ATIS的驾驶者的感知误差拉大时，影响效应也随之增大.

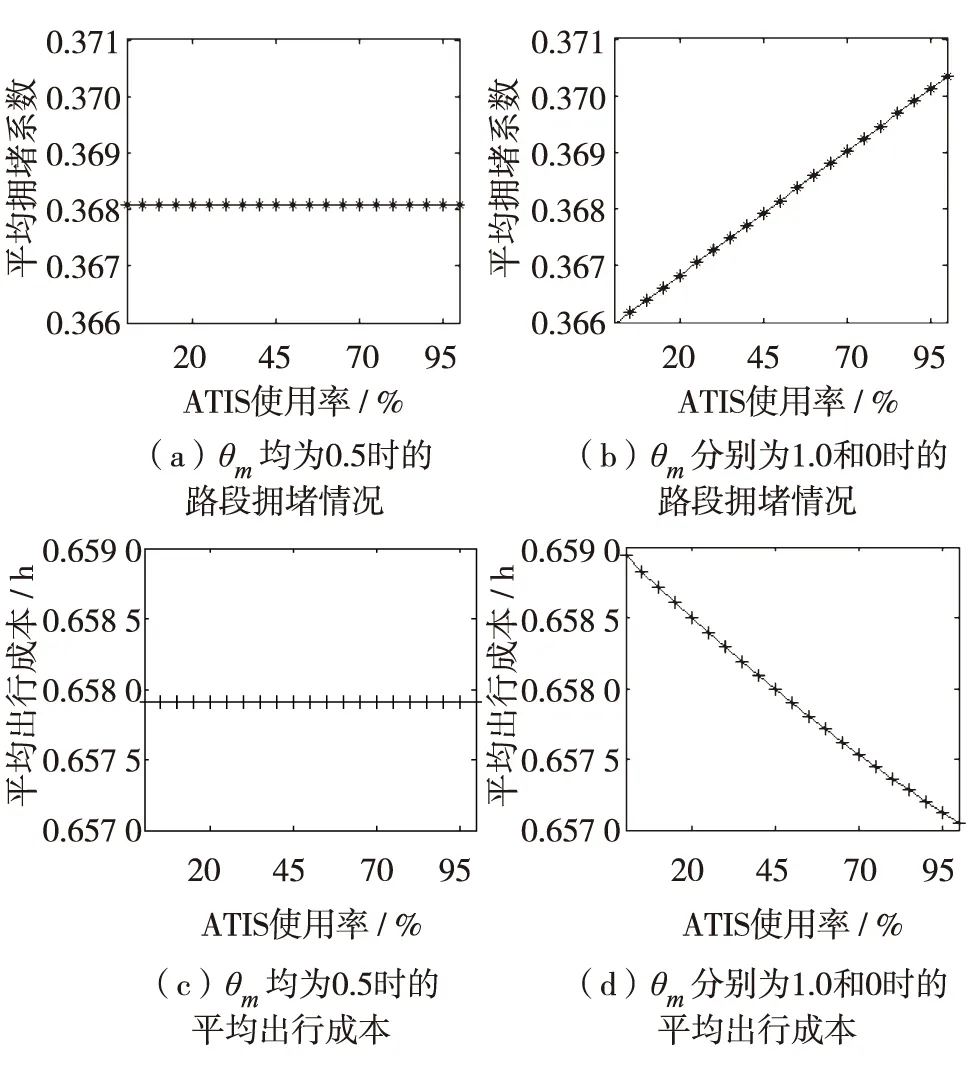
图5 θm可变时ATIS使用率的影响分析Fig.5 Analysis of ATIS usage rate with variable θm

接下来研究高收入比例和时间价值λ2可变时，ATIS对交通均衡的影响．如图6，随着高收入人群和时间价值的增加，人们越来越看重拥堵系数．当高收入人群占20%，λ2=135时，平均拥堵系数和出行成本的变化幅度明显减小．但当高收入人群达到90%，时间价值λ2=135时，平均拥堵系数开始随着ATIS使用率的提高而减少，驾驶者平均出行成本反而增加.

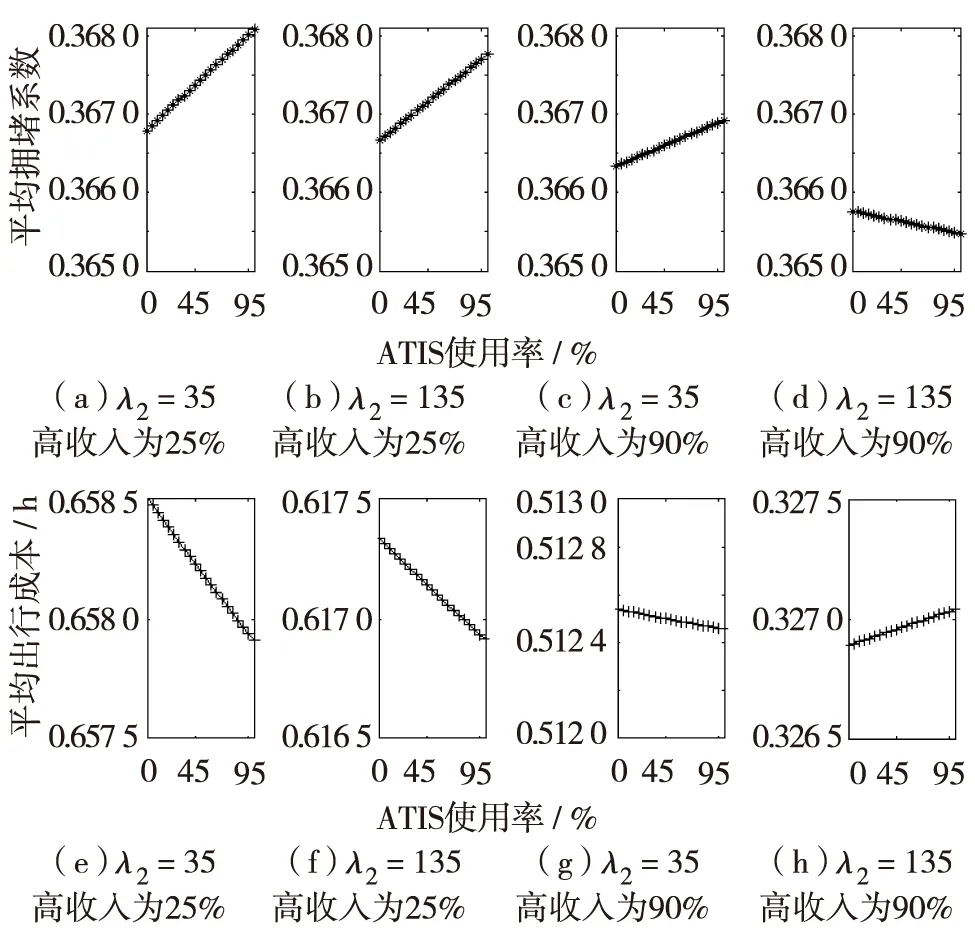
图6 λm参数和高收入比例可变时，ATIS使用率的影响分析Fig.6 Analysis of ATIS usage rate with variable λm and high income ratio

总之，人们会根据自己的收入水平，利用ATIS来选择是要减少平均拥堵系数还是平均出行成本. 在现今经济水平下，随着ATIS使用率的提高，交通均衡时的平均拥堵系数随之增大，而平均出行成本下降. 但当高收入人群达到一定比例，且人们的时间价值提升后，ATIS使用率的提高会降低平均拥堵系数，增加平均出行成本.

4 灵敏度分析

4.1 感知误差θm的分析

本节对感知误差θm进行灵敏度分析．由于使用ATIS的θm值肯定大于不使用的情况．所以，使用ATIS的θm取值为0.2～1.0，不使用ATIS的θm取值为0～0.5，均以0.1为变动量.

由图7发现，无论使用和不使用ATIS，θm值增大时，平均拥堵系数均会随之增加，平均出行成本随之减少.θm值的增大会使得驾驶者有更多机会选择出行路径，从而达到自己的意愿. 在现今经济水平下，人们会减少平均出行成本. 当经济水平发展到一定程度时，如图6的高收入人群达到90%，且时间价值λ2=135，人们就会选择减少平均拥堵系数.

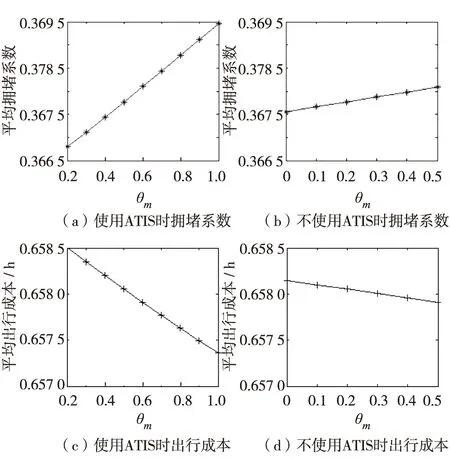
图7 θm参数分析Fig.7 Analysis of parameter θm

4.2 时间价值参数分析

低收入的时间价值λ1肯定小于高收入的λ2，所以λ1取值为5～35，λ2取值为20～120，均以5为变动量.

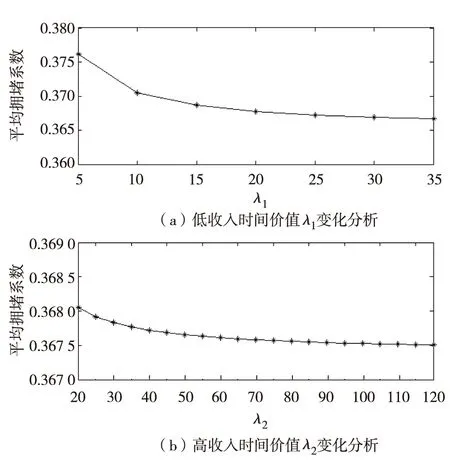
图8 λm参数分析Fig.8 Analysis of parameter λm

由图8发现，λ1和λ2的增加，路段平均拥堵系数随之下降. 观察图形的斜率，发现平均拥堵系数下降的幅度会随着人们时间价值的增加而减小. 尤其是在高收入人群的时间价值达到一定程度，人们出行的平均拥堵系数的变化更是非常微小.

结 语

ATIS可以很好减少路段的拥堵系数并降低出行者的出行成本. 但是，拥堵系数与出行成本很难同时达到最优. ATIS对交通均衡有影响. 在现今状况下，随着ATIS使用率的增加，如果使用其以减少出行成本，反而会加大道路平均拥堵系数. 通过对感知误差和时间价值等参数进行灵敏度分析可知，无论是否使用ATIS，感知误差增大都可以使驾驶者更好地按照自己的意愿选择出行路径. 随着时间价值增加，人们会更看重路段拥堵系数. 交通均衡是重要且必要的，但路段的平均拥堵系数和平均出行成本存在一定的矛盾. ATIS对交通均衡有影响，人们可以利用ATIS选择所需要的出行路径. 现今，人们倾向于利用ATIS牺牲拥堵系数来减少平均出行成本，经济水平提升后，人们才会慢慢利用ATIS选择可减少平均拥堵系数的路径.

致 谢：衷心感谢陆伟锋教授的悉心指导！

/ References：

[1] Wardrop J G. Some theoretical aspects of road traffic research[J]. ICE Proceedings: Engineering Divisions, 1952,3(1):325-362.

[2] Liu L N, McDonald J F. Economic efficiency of second-best congestion pricing schemes in urban highway systems[J]. Transportation Research Part B: Methodological, 1999,33(3):157-188.

[3] Maher M J, Hughes P C. A probit-based stochastic user equilibrium assignment model[J]. Transportation Research Part B: Methodological, 1997,31(4):341-355.

[4] Dial R B. A probabilistic multipath traffic assignment model which obviates path enumeration[J]. Transportation Research, 1971,5(2):83-111.

[5] Yai T, Iwakura S, Morichi S. Multinomial probit with structured covariance for route choice behavior[J]. Transportation Research Part B: Methodological, 1997,31(3):195-207.

[6] Daganzo C F, Sheffi Y. On stochastic models of traffic assignment[J]. Transportation Science, 1977, 11(3):253-274.

[7] Peng Xiang, Zhou Xinghui, Zhang Yong, et al. A model for evaluation of tax and fare policies in multimodal transportation networks[J]. Systems Engineering: Theory and Practice, 2014, 34(2): 494-501.(in Chinese) 彭 向, 周星慧, 张 勇, 等. 多模式交通网络税费政策评价模型[J]. 系统工程理论与实践, 2014, 34(2): 494-501.

[8] Xu Bing, Zhu Daoli. A multiclass and multicriteria stochastic traffic network equilibrium vibrational inequality model with fixed demand[J]. Journal of Highway and Transportation Research and Development, 2007, 24(4):129-133.(in Chinese) 徐 兵, 朱道立. 多用户多准则固定需求随机交通均衡变分模型[J]. 公路交通科技, 2007, 24(4): 129-133.

[9] Xu Bing, Zhu Daoli. Vibrational inequality equilibrium model for multiclass and multicriteria stochastic traffic networks with elastic demands[J]. Journal of Southwest Jiaotong University, 2008, 43(1): 114-119.(in Chinese) 徐 兵, 朱道立. 多用户多准则弹性需求随机交通均衡变分模型[J]. 西南交通大学学报, 2008, 43(1): 114-119.

[10] Huang Haijun, Wu Wenxiang. Model for evaluating impacts by travel information systems on travel behavior[J]. Systems Engineering: Theory and Practice, 2002, 22(10): 81-83.(in Chinese) 黄海军, 吴文祥. 交通信息对交通行为影响的评价模型[J]. 系统工程理论与实践, 2002, 22(10):81-83.

[11] Tsuji H, Takahashi R, Yamamoto Y. A stochastic approach for estimating the effectiveness of a route guidance system and its related parameters[J]. Transportation Science, 1985, 4(19):333-351.

[12] Kanafani A, Al-Deek H. A simple model for route guidance benefits[J]. Transportation Research Part B: Methodological, 1991, 25(4):191-201.

[13] Zhao Dan. Reconstruction mechanisms of commute trip chain under the integrate transportation information[D]. Beijing: Beijing Jiaotong University, 2013.(in Chinese) 赵 丹. 综合交通信息下通勤出行链重构机理研究[D]. 北京：北京交通大学, 2013.

[14] Lai Xinjun, Yu Zhi, Li Jun. Traffic impact analysis of pre-trip traffic information on urban network[J]. ACTA Scientiarum Naturalium University Sunyatseni, 2014, 53(2):12-17.(in Chinese) 赖信君, 余 志, 李 军. 出行前交通信息发布对城市路网的交通影响分析[J]. 中山大学学报自然科学版, 2014(2):12-17.

[15] Zhong Shaopeng, Lin Jinshan, Dend Wei. Stochastic traffic assignment model under ATIS and adverse weather conditions[J]. Systems Engineering: Theory and Practice, 2013, 33(5):1327-1334.(in Chinese) 钟绍鹏, 林锦山, 邓 卫. ATIS和恶劣天气下的随机交通分配模型[J]. 系统工程理论与实践, 2013, 33(5):1327-1334.

[16] Guo Renyong, Huang Haijun. Evolution model of multiclass and multicriteria stochastic equilibrium traffic assignment based on ATIS[J]. China Journal of Highway and Transport, 2008, 21(5):87-90.(in Chinese) 郭仁拥, 黄海军. 基于ATIS的多用户多准则随机均衡交通配流演化模型[J]. 中国公路学报, 2008, 21(5):87-90.

[17] Lam W H K, Shao H, Sumalee A. Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply[J]. Transportation Research Part B: Methodological, 2008, 42(10):890-910.

[18] Wu Pengkun, Tu Guoping, Wu Yuanyuan, et al. Urban population-economic distribution research at the perspective of mitigation traffic congestion[J]. Mathematics in Practice and Theory, 2014, 44(8):63-71.(in Chinese) 吴鹏昆, 涂国平, 吴园园, 等. 改善交通视角下的城市人口经济分布研究[J]. 数学的实践与认识, 2014,44(8):63-71.

[19] Transport commission of shenzhen municipality. Pengcheng traffic[EB/OL]. (2014-07-28). http://szmap.sutpc.com/index.aspx.(in Chinese) 深圳市交通运输委员会. 鹏城交通[EB/OL]. (2014-07-28) http://szmap.sutpc.com/index.aspx.

【中文责编：方 圆；英文责编：木 南】

Multiclass and multicriteria stochastic traffic network equilibrium model based on ATIS

Wu Pengkun1, Wu Yuanyuan2, and Xu Bing1†

1) School of Management, Nanchang University, Nanchang 330031, P.R.China 2) School of Economics and Management, Nanchang University, Nanchang 330031, P.R.China

We propose a multiclass and multicriteria traffic network equilibrium model to analyze the influence of advanced traveler information system (ATIS) on traffic equilibrium. In the model, all travelers are classified into four categories according to the market share of ATIS and the income differences of users. We make the route choice for each user according to Logit model based on the linear combination of travel time and travel cost. An origin-destination path in Meilin checkpoint in Shenzhen city of South China, is chosen to evaluate the influence of ATIS. The results reveal that travel cost and congestion coefficient cannot be reduced simultaneously. Under the current economic level, ATIS can help people decrease the average travel cost. With the economic development, people will be able to choose the path based on ATIS so as to reduce the average congestion coefficient. Finally, we lay special stress on sensitivity analysis of parameters in the model.

intelligent transportation system; advanced traveler information system; multiclass and multicriteria; traffic equilibrium; Logit stochastic equilibrium; origin-destination matrix

：Wu Pengkun，Wu Yuanyuan，Xu Bing．Multiclass and multicriteria stochastic traffic network equilibrium model based on ATIS[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 213-220.(in Chinese)

U 491.1

A

10.3724/SP.J.1249.2015.02213

国家自然科学基金资助项目(70961006)

吴鹏昆(1991—)，男(汉族)，江西省上饶市人，南昌大学博士研究生，E-mail：pengkunwu@126.com

Received：2014-10-14；Accepted：2015-01-20

Foundation：National Natural Science Foundation of China (70961006)

† Corresponding author：Professor Xu Bing．E-mail: xu_bing99@sina.com

引 文：吴鹏昆，吴园园，徐 兵．ATIS环境下的多用户多准则交通均衡模型分析[J]. 深圳大学学报理工版，2015，32(2)：213-220.