基于优化无迹Kalman滤波的电网动态谐波估计

江 辉，谢 兴，王志忠，彭建春

1)深圳大学光电工程学院，深圳 518060；2)深圳大学机电与控制工程学院，深圳 518060

【电子与信息科学 / Electronics and Information Science】

基于优化无迹Kalman滤波的电网动态谐波估计

江 辉1，谢 兴1，王志忠1，彭建春2

1)深圳大学光电工程学院，深圳 518060；2)深圳大学机电与控制工程学院，深圳 518060

提出一种基于粒子群优化的无迹卡尔曼滤波(particle swarm optimized unscented Kalman filter，PSOUKF)的电网动态谐波估计方法，利用包含种群分类与动态学习因子的改进粒子群优化算法，优化无迹卡尔曼滤波算法(unscented Kalman filter，UKF)的状态噪声协方差和观测噪声协方差，使系统噪声对电网动态谐波估计结果的影响得到充分考虑，克服了传统UKF算法将这两种方差视为常数导致的动态谐波估计精度低的缺陷. 仿真结果表明，PSOKUF算法比卡尔曼滤波(Kalman filter，KF)算法和传统的UKF算法更有效，在没有增加计算复杂度的情况下，能够提高动态谐波估计精度.

电力系统；电能质量；动态谐波估计；无迹卡尔曼滤波；粒子群算法；状态噪声协方差；观测噪声协方差

大容量与非线性电子元件在电力系统中的广泛应用会引起电网电压和电流波形的畸变，致使电网谐波和间谐波问题变得越来越突出. 然而，越来越多的敏感负荷，如可编程控制器、计算机和精密仪器等，却对电能质量提出了更高的要求. 因此，有必要准确地检测并给出电网谐波及间谐波参数，从而准确进行电网谐波评估和电网谐波治理.

经典电力系统谐波和间谐波分析方法主要包括：短时间傅里叶变换[1]、快速傅里叶变换[2](fast Fourier transform，FFT)、小波变换[3]、最小二乘法 (recursive least square，RLS)算法[4]、人工神经网络[5]、卡尔曼滤波[6](Kalman filter，KF)、集合卡尔曼滤波[7](ensemble Kalman filter，EnKF)和无迹卡尔曼滤波[8](unscented Kalman filter，UKF)等．文献[9]提出了一种高精度FFT的电网谐波分析，但FFT分析间谐波时，难以实现同步采样，基波和谐波频谱泄漏有可能淹没真实的间谐波．文献[10]介绍了应用插值FFT算法精确估计电网谐波参数，这种算法具有运算速度快、易于硬件实现等优点，克服了傅立叶变换频谱泄露的缺点，但算法的分辨率有限．文献[11]介绍了一种基于多频带小波的电力系统谐波分析法，提出了4种多频带小波函数及其相应的多频带小波变换．文献[12]介绍了一种基于RLS和KF算法的谐波估计，可以快速预测电力系统的谐波参数．文献[13]提出了一种智能神经网络快速电力系统谐波检测方法，在噪声环境下，能快速准确检测谐波. KF[6]、EnKF[7]和UKF[8]由于具有处理非线性系统的能力，在电力系统状态估计中得到了应用．文献[14]提出了一种基于自适应KF的谐波估计方法，通过对动态谐波系统的仿真，得出KF对谐波预测有很好的鲁棒性．文献[15]提出了一种基于EnKF的检测方法，可对高阶谐波和间谐波进行估计．文献[16]介绍了一种基于UKF的系统频率、幅值估计方法．

UKF是由扩展卡尔曼滤波(extended Kalman filter，EKF)发展而来，通过无迹变换近似获取非线性变换后的统计特性，无需计算雅克比矩阵，运算速度快，运算精度高．用常规UKF进行计算时，状态噪声协方差Q和观测噪声协方差R是基于UKF系统模型和当时的噪声环境所取的，且近似为常量．然而，电力系统干扰很多，系统中各种不断变化的噪声会对谐波估计产生影响，动态谐波随时间的变化幅值也会发生变化，因此进行谐波估计时，将状态噪声协方差和观测噪声协方差视为近似常量不能准确反映系统所处的环境，难以对谐波参数进行准确预测．为提高估计精度，本研究提出一种基于粒子群优化算法的无迹卡尔曼滤波方法(particleswarmoptimizedunscentedKalmanfilter，PSOUKF)，采用粒子群优化(particleswarmoptimization，PSO)算法[17]对状态噪声协方差和观测噪声协方差进行优化，在不增加计算复杂度的情况下，提高了动态谐波估计精度．

1 谐波信号模型

含噪声的n次离散化谐波信号可表示为

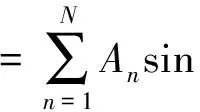
Adcexp(-αdckTs)+μ(k)

(1)

其中，N为谐波的总数；An为幅值；φn为相角；ωn=2πnf0；f0为基波频率；Ts为采样周期;k=t/Ts；Adcexp(-αdckTs)为直流分量;αdc和Adc为常量；μ(k)为随机噪声.

式(1)中，将Adcexp(-αdct)用泰勒展开，近似可得

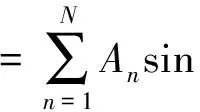
Adc-AdcαdckTs+μ(k)

(2)

将式(2)表示为式(3)矩阵形式

Y(k)=H(x)X(k)+υ(k)

(3)

其中，H(x)=[sin(ω1kTs) cos(ω1kTs) sin(ω2kTs) cos(ω2kTs) … sin(ωNkTs) cos(ωNkTs) 1 -kTs]为状态转移矩阵；υ(k)为第k时刻的噪声矩阵[18-19]；X(k)可表示为

X(k)=[x1kx2(k) …x2n(k)AdcAdcαdc]T

(4)

这里，x2i(k)=A2icosφ2i;x2i+1(k)=A2i+1sinφ2i+1;i=0,1,…,N-1.X(k)通过式(5)进行更新

X(k)=X(k-1)+W(k-1)

(5)

其中，W(k-1)为第k-1时刻的噪声矩阵．

通过X(k)中的各个分量间的关系，可求出谐波的幅值和相角[20]．

2 UKF基本原理

UKF的本质是一种基于蒙特卡罗方法的卡尔曼滤波，适用于解决非线性问题[21]. 其基本思想是选择一组确定的带权值的粒子集合(Sigma点集)，使这些点的均值和方差等于状态分布的均值和方差，然后，将这些点代入非线性函数得到新的Sigma点集，并通过新点集得到变换后的均值和方差[19]. 与EKF滤波相比，UKF能更精确地拟合非线性函数. 本研究用UKF对电网谐波进行估计．

设随机非线性离散方程为

Xk=f(Xk-1)+Wk-1

(6)

Yk=h(Xk-1)+υk-1

(7)

其中，f(Xk-1)=X(k-1)；h(Xk-1)=H(k-1)X(k-1)；Xk为状态变量；Yk为观测变量；R和Q为两个互不相关的高斯噪声Wk-1和υk-1的协方差，且均值为0.

1) 扩展状态方程的初始值．

P0=(X0-X)(X0-X)T

(8)

其中，P0为误差协方差；X0为初始理论值；X为X0的期望，即X=E[X0]．

2) 计算Sigma点．

χk-1=[Xk-1,Xk-1+ζk-11,Xk-1+ζk-12,…,

Xk-1+ζk-1n,Xk-1-ζk-11,…,

Xk-1-ζk-1n]

(9)

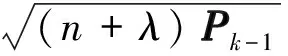
3) 预测状态方程．

为得出每点的预测状态值，Sigma点通过式(10)进行计算

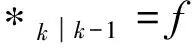
(10)

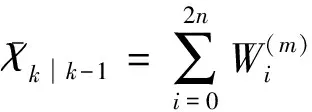
(11)

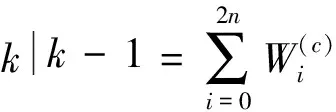
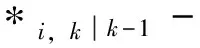
(12)

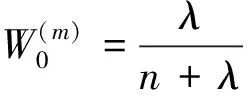
4) 预测观测方程．

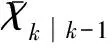
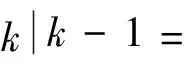
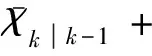
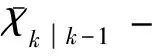
(13)

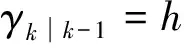
(14)

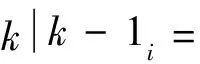
(15)

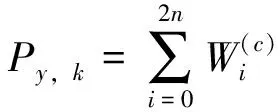
(16)

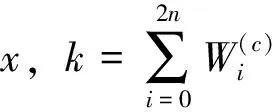
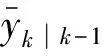
(17)

5) 计算滤波增益Kk、 修正下一时刻的协方差Pk、 状态值Xk和测量误差ek，依次为

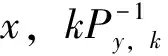
(18)

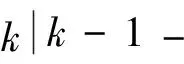
(19)

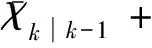
(20)

(21)

然后，以k时刻的值再去预测下一时刻的值，依次递归，可得到完整的系统预测．

按照传统的UKF方法，状态噪声协方差Q和观测噪声协方差R依照系统模型所处的噪声环境取近似常量，不能实现谐波的准确估计，有必要对这两个参数进行实时优化，以提高预测的准确性．本研究采用改进的基于种群分类与动态学习因子的粒子群算法对这两个噪声协方差进行实时优化．

3 基于粒子群优化算法的无迹卡尔曼滤波

3.1 粒子群算法原理

PSO算法是从一组随机解出发，采用迭代的方法寻找最优解，用适应度来评价解的优劣，并通过追随当前搜索到的群体最优解和个体最优解来寻找全局最优[17]．PSO算法没有遗传算法的交叉和变异操作，因此比遗传算法的规则更简单[22]．

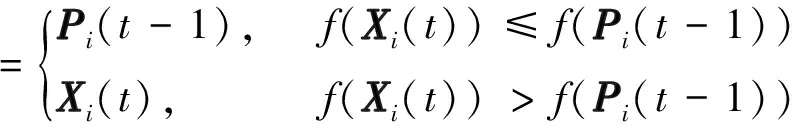
(22)

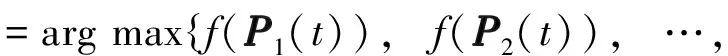
(23)

其中，Pi(t)为第t次迭代后第i个粒子所记忆的位置，本研究中代表最优测量误差； G(t)为第t次迭代后整个群体记忆的最佳位置，f(·)为适应度函数； M为粒子总数；i=1，2，…，M．

惯性权重线性下降的PSO算法和收缩因子模型的PSO算法，在高维复杂问题寻优时，仍存在易于陷入局部最优解和收敛精度低的缺点[18]. 为此，本研究采用一种基于种群分类与动态学习因子的PSO改进算法. 改进PSO算法的速度更新公式为

1)当Vmin≤Vid(t)≤Vmax时，

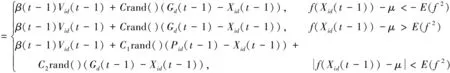
(24)

其中，β(t-1)=(tmax-t)/tmax为t-1次迭代的权重；函数rand()表示0～1之间的某一随机数；C为常数，C1=2/(1+t0.25)，C2=t/tmax，t为当前迭代次数，tmax为最大迭代次数；f(Xid(t-1))为粒子i的适应值；Vid(t)为速度向量Vi(t)中的任一元素；μ为第t-1次迭代后全部粒子适应度的均值；E(f2) 为第t-1次迭代后全部粒子适应度的2阶原点矩；Vmax为速度向量元素中的最大值；Vmin为速度向量元素中的最小值；Xid(t)为Xi(t)中的任意元素；Pid(t)为Pi(t)中的任意元素；Gd(t)为G(t)中的任意元素．

2)当Vid(t)≥Vmin和Vid(t)≥Vmax时，

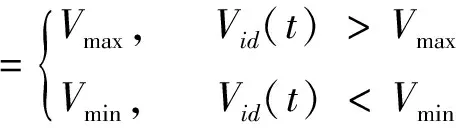
(25)

对每个粒子的位置Xi(t-1)更新如下

Xi(t)=Xi(t-1)+Vi(t)

(26)

为使状态噪声协方差和观测噪声协方差能准确反应系统谐波情况，提高UKF谐波估计的估计精度，构造适应度函数f(·)，第m个粒子的适应度函数为

(27)

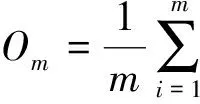
(28)

其中，Py,k为观测方程预测中的协方差．

通过最大化适应度函数fm，可得到最优测量误差，继而优化状态噪声协方差和观测噪声协方差．

3.2 状态噪声协方差和观测噪声协方差估计

状态噪声协方差和观测噪声协方差与系统的测量误差有关，通过PSO算法得到全局优化值G(t)，则所对应的最优测量误差为ebest，利用ebest对状态噪声协方差和观测噪声协方差进行估计[18]． 状态噪声协方差估计为

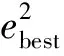
(29)

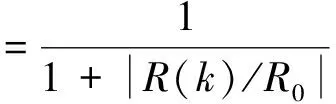
(30)

其中，R0为观测噪声协方差的初始值；R(k)为第k时刻的观测噪声协方差．

状态噪声协方差Q的估计可用处理状态噪声协方差估计的方法进行计算，Q=qIn×n，n为预测空间的维数，估计公式为

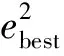
(31)

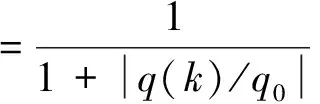
(32)

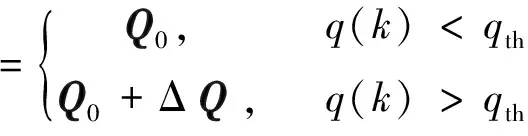
(33)

其中，qth为阀值常数；Q0=q0In×n是状态噪声协方差初值； ΔQ为常量．

3.3 基于PSO的协方差估计步骤

1)设置PSO初值．设置参数C、C1、C2、Vmax、Vmin和qth．

2)计算ek和Vi． 通过式(21)中获取测量误差ek初值，通过式(27)计算第k个粒子适应度函数fk，通过式(24)和式(25)更新相应的速度向量Vi．

3) 估计状态噪声协方差和观测噪声协方差．首先，利用式(22)和式(23)确定Pi(k)和G(t)，得到最优的适应度值fbest及对应的测量误差ebest． 然后，按照式(29)至(33)得到下一时刻的状态噪声协方差和观测噪声协方差．最后，回到步骤2)，估计下一时刻值．

3.4 基于PSOUKF谐波估计步骤

1) 赋初值．通过式(8)计算初始时刻t(k-1)的系统协方差P0，并给R0、Q0和ΔQ赋初值. 初值选取很重要，会影响状态估计精度．

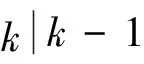
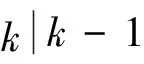
4 仿真与分析

为比较改进型UKF算法和现有KF和UKF等算法对电网谐波的估计性能，引入性能指标函数——均方根误差(rootmeansquareerror，RMSE)来衡量预测值与理论值之间的偏差．在时刻的均方根误差为

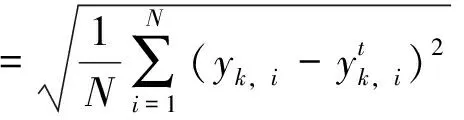
(34)

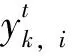
本研究采用Matlab2008b版进行仿真，信号采样频率为fs=2.5 kHz，采样间隔Δt=0.4 ms, 基波频率f=50 Hz．

4.1 直流衰减的谐波信号幅值估计

含直流衰减的多次谐波电压信号可以描述为

y(t)=[1.5+a1(t)]sin(ωt+80°)+

[0.5+a2(t)]sin(3ωt+60°)+

0.5exp(-5t)+0.005μ(t)

(35)

其中，μ(t)表示均值为0和方差为1的随机噪声；谐波信号的幅值随a1(t)、a2(t)和a3(t)变化为

a1(t)=0.15sin(2πf1t)+

0.05sin(2πf5t)

(36)

a2(t)=0.05sin(2πf3t)+

0.01sin(2πf5t)

(37)

其中，f1=1.0 Hz；f3=3.0 Hz；f5=6.0 Hz．

图1为基波幅值信号的跟踪波形图．从图1可见，用本研究提出的估计方法得到的基波曲线与实际信号曲线基本重合．表1为3种方法在t=0.02 s时的误差分析，该时刻的理论幅值为1.553 0 p.u．从表1可见，与KF和UKF方法相比，PSOUKF方法在t=0.02 s时刻的相对误差和RMSE值最小，与理论幅值近似相等. 因此，PSOUKF方法显优于KF和UKF方法．

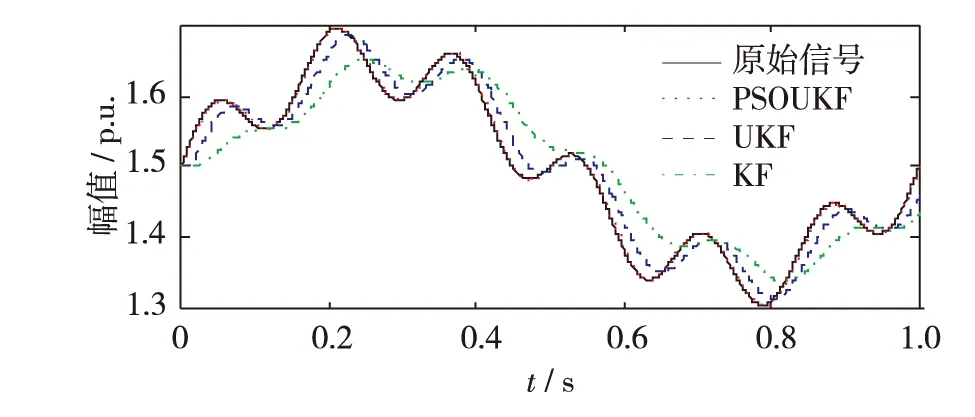
图1 基波幅值估计Fig.1 (Color online)Estimation of amplitude of the fundamental wave

表1 基波幅值误差分析(t=0.02 s)

Table 1 Error analysis of amplitude of the fundamental wave (t=0.02 s)

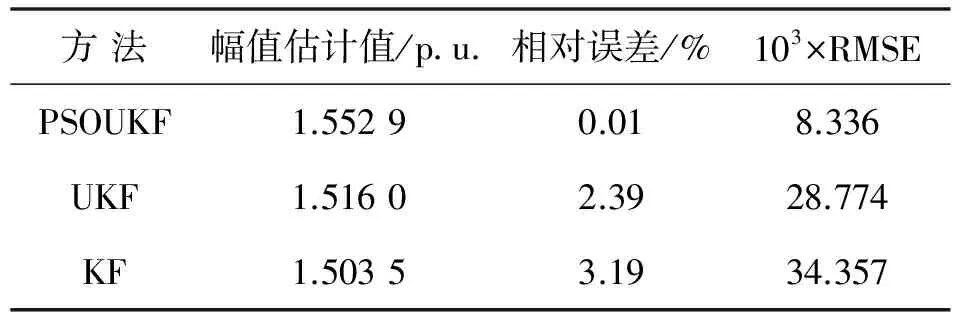
方法幅值估计值/p u 相对误差/%103×RMSEPSOUKF1．55290．018．336UKF1．51602．3928．774KF1．50353．1934．357

图2为3种方法对3次谐波幅值的跟踪波形图和RMSE曲线图.

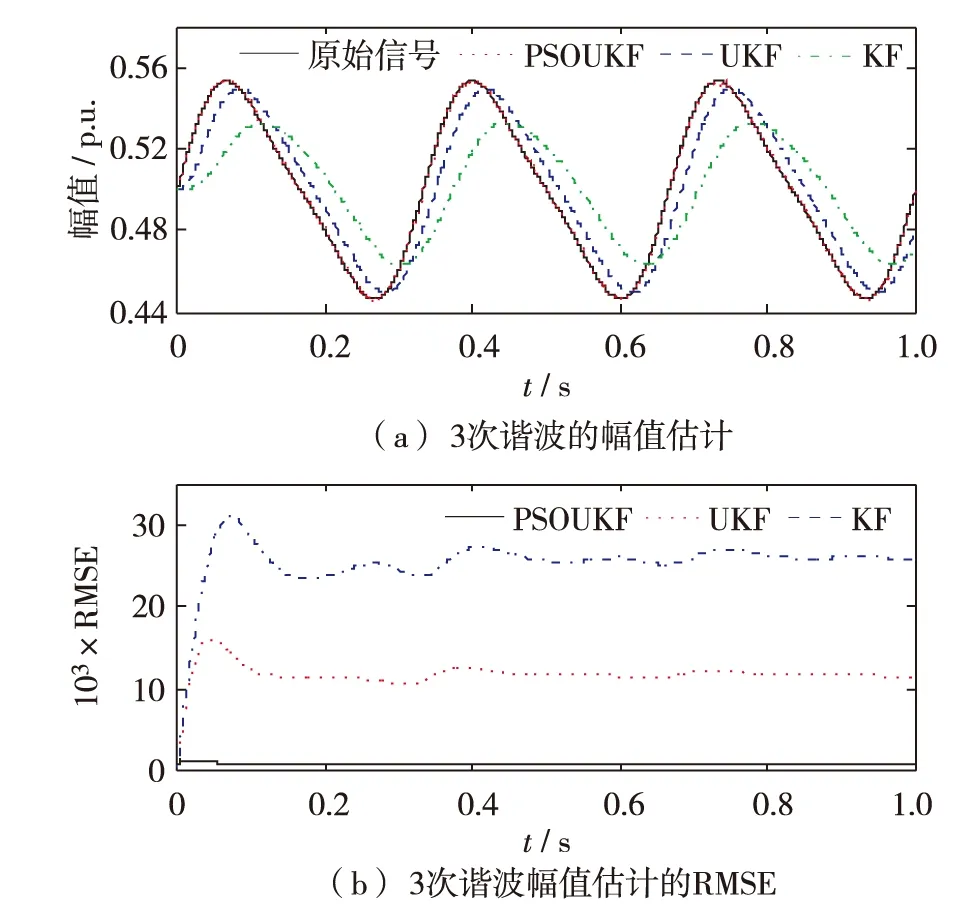
图2 第3次谐波幅值估计Fig.2 (Color online) Estimation of amplitude of the 3rd harmonic

从图2(a)可见，在幅值估计上，PSOUKF较UKF和KF更接近真实值．从图2(b)也可见，PSOUKF的RMSE曲线明显小于UKF和KF的曲线. 表2为3种方法在t=0.02 s时幅值误差分析表，该时刻的理论幅值为0.525 3 p.u.．从表2 可见，PSOUKF在此时刻的相对误差和RMSE值都比其他2种方法的值小．

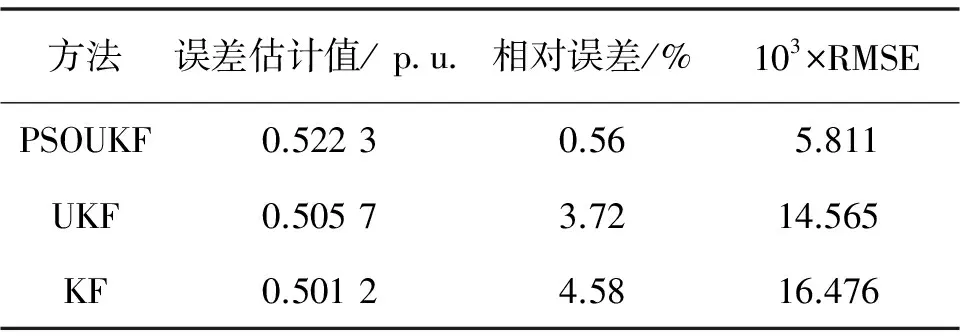
表2 三次谐波幅值误差分析(t=0.02 s)

综上所述，PSOUKF对谐波幅值的估计明显优于KF和UKF方法．

4.2 直流衰减的动态谐波信号相角估计

y(t)=1.5sin[ωt+80°+a1(t)]+

0.5sin[3ωt+60°+a2(t)]+

0.5exp(-5t)+0.005μ(t)

(38)

其中，μ(t)是均值为0和方差为1的随机噪声；谐波信号的相角a1(t)和a2(t)的变化为

a1(t)=0.15sin(2πf1t)+

0.5sin(2πf5t)

(39)

a2(t)=0.5sin(2πf3t)+

0.2sin(2πf5t)

(40)

其中，f1=1.0 Hz；f3=3.0 Hz；f5=6.0 Hz．

图3给出了基波相角信号的跟踪波形图．表3为3种方法在t=0.02 s时的相角误差分析表，此时的理论相角为80.530 3°．

表3 基波相角误差分析(t=0.02 s)

Table 3 Error analysis of fundamental wave phase (t=0.02 s)

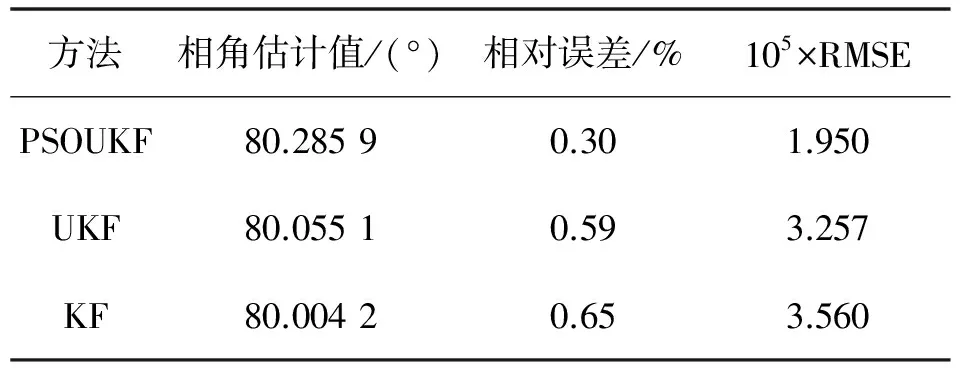
方法相角估计值/(°)相对误差/%105×RMSEPSOUKF80．28590．301．950UKF80．05510．593．257KF80．00420．653．560

由图3可见，PSOUKF的跟踪曲线明显优于UKF和KF．从表3可见，PSOUKF在t=0.02 s时与理论值的相对误差为0.3%，RMSE值为1.949 7×10-5，比KF和UKF在此时刻的数值都小．

综合图3和表3可见，PSOUKF对基波相角的跟踪要优于KF和UKF方法.

图4(a)给出3次谐波相角信号的跟踪波形图. 图4(b)为3种方法的RMSE曲线图．表4为3种方法在t=0.02 s时的误差分析表，此时理论相角为60.321 0°.

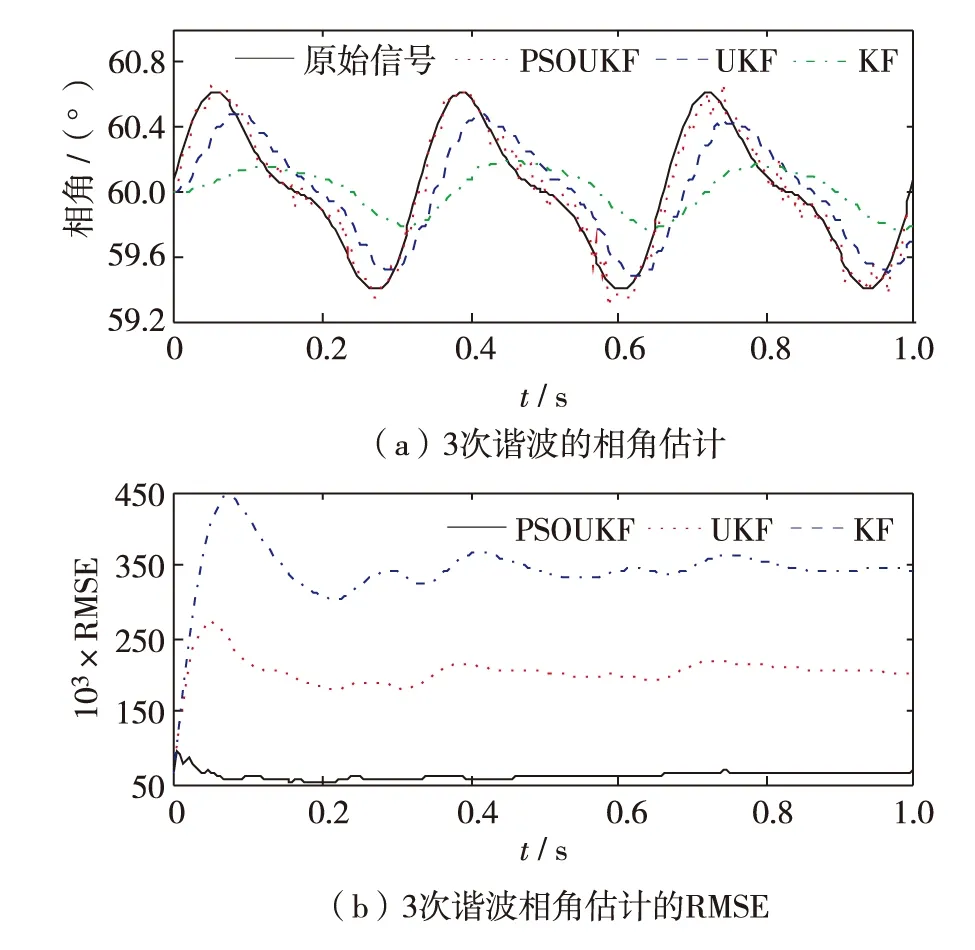
图4 第3次谐波估计Fig.4 (Color online) Estimation of the 3rd harmonic phase

表4 第3次谐波相角误差分析(t=0.02 s)

Table 4 Error analysis of the 3rd harmonic wave phase (t=0.02 s)

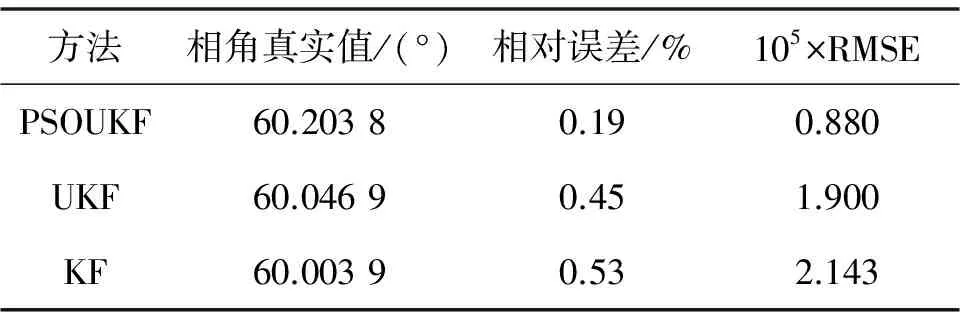
方法相角真实值/(°)相对误差/%105×RMSEPSOUKF60．20380．190．880UKF60．04690．451．900KF60．00390．532．143

由图4和表4可见，PSOUKF方法对第3次谐波的相角估计要优于KF和UKF的方法．对于第5和第7次谐波，PSOUKF在谐波幅值和相角仿真上也得到了同样结论，限于篇幅，这里没有给出详细结果．

仿真实验说明，通过对UKF状态噪声协方差和观测噪声协方差进行优化，可以提高谐波幅值和相角的估计精度，很好反映电网系统所处的环境．PSOUKF估计精度高，估计效果优于KF和UKF算法，尤其是在幅值估计上表现明显．

结 语

本研究提出PSOUKF滤波新方法，对电网动态谐波进行估计. 仿真分析表明，PSOUKF方法适用于电网动态谐波的估计，能准确估计电网动态谐波幅值和相角，检测精度高，跟踪速度快. PSOUKF方法用于动态谐波估计时优于KF和UKF方法，如何将PSOUKF方法用于更加复杂的动态环境下，将是下一步研究的重点．

/ References：

[1] Paul S W．Short-time Fourier transforms and Wigner-Ville distributions applied to the calibration of power frequency harmonic analyzers[J]．IEEE Transactions on Instrumentation and Measurement，1999，48(2)：475-478．

[2] Li Jiasheng，Chai Shijie．Research of online rapid detetion method about harmonic and inter-harmonic of power quality[J]．Power System Protection and Control，2009，37(18)：62-69．(in Chinese) 李加升，柴世杰．电能质量谐波间谐波在线快速检测方法研究[J]．电力系统保护与控制，2009，37(18)：62-69．

[3] Zhang Xiaotao，Xing Baoqin，Wang Aijun，et al．Harmonic current montitoring and line loss analysis based on wavelet transform[J]．Power System Protection and Control，2013，41(22)：79-83．(in Chinese) 张小桃，邢宝钦，王爱军，等．基于小波变换的谐波电流监测及线损分析[J]．电力系统保护与控制，2013，41(22)：79-83．

[4] Ray P K，Subudhi B. BFO optimized RLS algorithm for power system harmonics estimation[J]．Applied Soft Computing，2012，12(8)：1965-1977．

[5] Zhang Qian，Wang Haona，Fu Zhihong，et al．An approach with filters-neural network for harmonic detection[J]．Power System Protection and Control，2011，39(12)：42-47．(in Chinese) 张 谦，王好娜，付志红，等．滤波器：神经网络的谐波检测方法[J]．电力系统保护与控制，2011，39(12)：42-47．

[6] Rosendo Macías J A，Expósito A G．Self tuning Kalman filters for harmonic computation[J]．IEEE Transactions on Power Delivery，2006，21(1)：501-503．

[7] Luo X，Moroz I M．Ensemble Kalman filter with the unscented transform[J]．Physica D：Nonlinear Phenomena，2009，238(15)：549-562．

[8] Rambabu K，Bjarne F，Lars I．Applying the unscented Kalman filter for nonlinear state estimation[J]．Journal of Process Control，2008，18(7/8)：753-768．

[9] Hu Zhenhua，Wang Haibin，Zhang Jianyi．FFT algorithm with high accuracy for harmonic analysis in industry power system[J]．Proceedings of CSU-EPSA，2009，21(3)：46-52.(in Chinese) 胡振华，王海滨，张健毅．工业电力系统谐波分析的高精度FFT算法[J]．电力系统及自动化学报，2009，21(3)：46-52．

[10] Qi Caijun, Chen Longdao, Wang Xiaohai. High-accuracy estimation of electrical harmonic parameters by using the interpolation FFT algorithm[J]．Journal of Zhejiang University Engineering Science，2003，18(1)：92-95．(in Chinese) 祁才君，陈隆道，王小海．应用插值FFT算法精确估计电网谐波参数估计[J]，浙江大学学报工学版，2003，18(1)：92-95.

[11] Ren Zhen，Huang Qungu，Huang Wenying，et al．New methods of power system harmonic analysis based on wavelet transform with multi-frequency band[J]．Proceedings of the CSEE，2000，20(12)：38-41．(in Chinese) 任 震，黄群古，黄雯莹，等．基于多频带小波变换的电力系统谐波分析新方法[J]．中国机电工程学报，2000，20(12)：38-41．

[12] Subudhi B，Ray P K．Estimation of power system harmonics using hybrid RLS-adaline and KF-adaline algorithms[C]// IEEE Region 10 Conference?TENCON．Singapore：IEEE Press，2009：1-6．

[13] Hsiung C L．Intelligent neural network-based fast power system harmonic detection[J]．IEEE Transactions on Industrial Electronics，2007，54(1)：43-52．

[14] Yu K K C，Watson N R，Arrillaga J．An adaptive Kalman filter for dynamic harmonic state estimation and harmonic injection tracking[J]．IEEE Transactions on Power Delivery，2005，20(2)：1577-1584．

[15] Ray P K，Subudhi B. Ensemble-Kalman-filter-based power system harmonic estimation[J]．IEEE Transactions on Instrumentation and Measurement，2012，61(12)：3216-3224．

[16] Novanda H，Regulski P，Gonzalez-Longatt F M，et al．Unscented Kalman filter for frequency and amplitude estimation[C]// IEEE Trondheim Power Technology Trondheim(Norway)：IEEE Press，2011：1-6．

[17] Bi Xiaojun．Information intelligent processing technology[M]．Beijing：Publishing House of Electronics Industry，2010：332-342．(in Chinese) 毕晓君．信息智能处理技术[M]．北京：电子工业出版社，2010：332-343．

[18] Reddy J B V，Dash P K，Samantaray R，et al．Fast tracking of power quality disturbance signals using an optimized unscented filter[J]．IEEE Transactions on Instrumentation and Measurement．2009，58(12)：3943-3952．

[19] Chen Chen，Cheng Yinhang．Simulation research of SLAM algorithm based on iterated unscented Kalman filter[J]．Journal of System Simulation，2012，24(8)：1643-1650．(in Chinese) 陈 晨，程荫杭．基于迭代无迹卡尔曼滤波的SLAM算法仿真研究[J]．系统仿真学报，2012，24(8)：1643-1650．

[20] Alcaraz R，Bueno E J，Cobreces S ，et al．Power system voltage harmonic identification using Kalam filter[C]// The 12th International Power Electronics and Motion Control Conference．Portoroz(Slovenia)：IEEE Press，2006：1283-1288．

[21] Wang Pin，Xie Weixin，Liu Zongxiang，et al．Performance evaluation of several methods for tracking a ballistic object[J]．Journal of Shenzhen University Science and Engineering，2012，29(5)：392-398．(in Chinese) 王 品，谢维信，刘宗香，等.几种面向弹道目标跟踪算法的性能评估[J]．深圳大学学报理工版，2012，29(5)：392-398．

[22] Xue Liping，Yin Junxun, Ji Zhen，et al．Speaker recognition based on particle swarm optimizition and fuzzy clustering analysis[J]．Journal of Shenzhen University Science and Engineering，2008，25(2)：178-183．(in Chinese) 薛丽萍，尹俊勋，纪 震.基于粒子群优化-模糊聚类的说话人识别[J]．深圳大学学报理工版，2008，25(2)：178-183．

【中文责编：方 圆；英文责编：木 南】

Dynamic harmonic estimation based on optimized unscented Kalman filter model

Jiang Hui1†, Xie Xing1, Wang Zhizhong1, and Peng Jianchun2

1) College of Optoelectronic Engineering ,Shenzhen University, Shenzhen 518060,P.R.China 2) College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen 518060, P.R.China

We propose a particle swarm optimized unscented Kalman filter (PSOUKF) method to estimate the power system dynamic harmonics. By using the improved particle swarm optimization algorithm with species classification and dynamic learning factor, we optimize the state noise covariance and the measurement noise covariance of the unscented Kalman filter (UKF) so as to sufficiently take the impacts of power system noise on dynamic harmonic estimation into account. The proposed method overcomes the deficiency of low dynamic harmonic estimation accuracy in the traditional UKF method in which the above two kinds of covariance are taken as constants. Simulation results show that the proposed PSOUKF is more effective than Kalman filter (KF) and UKF, and PSOUKF can improve the dynamic harmonic estimation accuracy without increasing the computational complexity.

power system; power quality; dynamic harmonic estimation; unscented Kalman filter; particle swarm optimization; state noise covariance; measurement noise covariance

：Jiang Hui，Xie Xing，Wang Zhizhong，et al. Dynamic harmonic estimation based on optimized unscented Kalman filter model[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 188-195.(in Chinese)

TM 711；TM 93

A

10.3724/SP.J.1249.2015.02188

国家自然科学基金资助项目(51177102)；深圳市基础研究计划项目(JCYJ20140418193546100，JCYJ20120817164050203)

江 辉(1968—)，女(汉族)，湖南省常德市人，深圳大学教授．E-mail: huijiang@szu.edu.cn

Received：2014-10-04；Accepted：2014-12-29

Foundation：National Natural Science Technology of China (51177102)；Shenzhen Science and Technology Research Foundation for Basic Project (JCYJ20140418193546100，JCYJ20120817164050203)

† Corresponding author：Professor Jiang Hui．E-mail: huijiang@szu.edu.cn

引 文：江 辉，谢 兴 ，王志忠，等．基于优化无迹Kalman滤波的电网谐波估计[J]. 深圳大学学报理工版，2015，32(2)：188-195.