波导滤波器的等效电路模型及实验研究
2015-04-27储建华钱荣荣王传齐
储建华,钱荣荣,王传齐
1) 苏州工业职业技术学院机电工程系,苏州 215104; 2) 中国科学院合肥物质科学研究院,合肥 230031

【电子与信息科学 / Electronics and Information Science】
波导滤波器的等效电路模型及实验研究
储建华1,2,钱荣荣2,王传齐2
1) 苏州工业职业技术学院机电工程系,苏州 215104; 2) 中国科学院合肥物质科学研究院,合肥 230031
建立同轴腔加载波导滤波器系统的等效电路模型,在波导短路端面与同轴探针弱耦合状态下,通过求解回路方程组得到3个谐振频率点,分别对应π/2模、0模和π模,频率间隔决定于耦合系数.强耦合状态下,该模型仅存在1个谐振频率点,波导只起传输信号及滤波作用.通过实验测量波导滤波器系统正向传输系数曲线,在弱耦合状态下获得3个谐振频率点,强耦合状态下仅存在1个谐振频率点,结果与理论分析一致.
微波技术;波导;同轴腔;波导滤波器;等效电路模型;高次模;耦合系数
随着微波器件向高频率和高功率方向发展,对圆柱形同轴腔高次模式的研究日渐增多[1-5].高次模式适合对功率要求强于对信号频宽要求的情形.采用高次模式有利于增大腔体横截面面积,减轻阴极负荷,降低管子的工作电压,获得高脉冲功率和大平均输出功率.同时,在高频段,工作模式与邻近的非工作模式之间有一定的频率间隔,这有利于信号输出和滤波.将同轴腔高次模式用于真空中电子束流参数测量已引起学者的广泛关注,用该方法测量的分辨率可达到亚微米量级[6-10].无论高功率微波信号的产生还是真空中电子束流参数测量,都需要解决同轴腔基模信号滤除以及高次模信号耦合输出这两个主要问题[11-12].本研究以用于真空中电子束流测量的同轴腔加载波导滤波器为研究对象,利用波导滤波器滤除同轴腔基模信号和耦合输出高次模信号,建立波导滤波器等效电路模型,研究强耦合与弱耦合状态下的特性,给出系统试验结果,对于高次模信号的利用及耦合输出系统的设计具有一定的借鉴作用.
1 同轴腔加载波导滤波器
同轴腔高次模式用于真空中电子束流参数测量的主要原理是,圆柱形同轴腔中电子束流主要激励起基模TM010信号及高次模TM110信号.其中,高次模TM110信号与电子束流相对腔轴偏移量成正比,根据TM110模信号强度可测量束流位置.因此,耦合输出TM110高次模信号并且抑制TM010基模信号输出成为关键难点.
利用波导滤波器可实现同轴腔TM010基模信号的滤除和TM110高次模信号的耦合输出.根据电磁场分布特性,将圆柱形同轴腔中TM110高次模与波导中TE10模耦合,选取合适的波导尺寸,当波导宽度a与TE10模波长λ满足a<λ<2a时,仅TE10模式传播,其他模式都处于截止状态.波导TE10模电场只有单向分量,在波导中获得单方向极化,因此可在波导中插入同轴探针耦合输出信号.此外,根据电磁场分布特性,圆柱形同轴腔中TM010基模与波导中TE10模不能有效耦合,并且选择TM010基模信号波长大于2a,则进一步抑制TM010基模与波导模式的耦合,因此波导滤波器可有效滤除TM010基模信号.
本研究研制的同轴腔加载波导滤波器系统如图1.其中,圆柱形同轴腔长度为20mm,内直径为64mm,外直径为74mm,矩形波导横截面尺寸为28.5mm×12.6mm,对称分布4个矩形波导与同轴腔耦合槽焊接在一起.与耦合槽构成完整波导滤波耦合输出结构.

图1 同轴腔加载波导滤波器系统Fig.1 Coaxial cavity loaded with waveguide filter
利用三维电磁场软件HFSS(highfrequencystructuresimulator)仿真同轴腔加载波导滤波器系统电磁场分布,结果如图2.由TM010模的电场强度分布可见,其电场完全限制在同轴腔内部,波导中并无耦合输出.TM110模的电场强度分布状况反映了波导有效耦合输出TM110模信号,波导中心处电场最强,可在波导中心插入同轴探针耦合输出信号.
2 单波导与同轴腔耦合等效电路
图2中纵向极化的TM110模通过横向对波导耦合输出;与之相反,横向极化的TM110模通过纵向对波导耦合输出.其中,1,2,3,4,5表示端口.在忽略相邻波导耦合的情况下,端口1和2对应的横向对波导与同轴腔耦合情况可用2端口网络来描述,端口3和4对应的纵向波导与同轴腔耦合等效为另一个2端口网络.
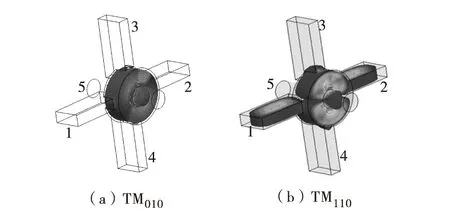
图2 TM010和TM110电场强度分布Fig.2 Electric field distributions of TM010 and TM110
波导与同轴腔的耦合可用等效电路模型来表示.先考虑单个波导与圆柱形同轴腔的电耦合情况,等效电路如图3,同轴腔用并联等效谐振电路表示,等效电感、电容和电导分别是L1、C1和G1,TM110模本征频率为f1,波导的特征导纳为Y0,SS′为失谐短路面,同轴腔与波导之间耦合可等效成从同轴腔到波导的变比为n∶1的理想变压器,则波导的特征导纳Y0变换到同轴腔内时有Y0′=Y0/n2. 波导对同轴腔影响相当于在同轴腔并联等效电路中增加损耗电导Y0′,则同轴腔有载品质因数QL[13]为
QL=2πf1C1/(G1+y0′)
(1)
波导与同轴腔间的耦合系数β为
β=Y0/(n2G1)
(2)
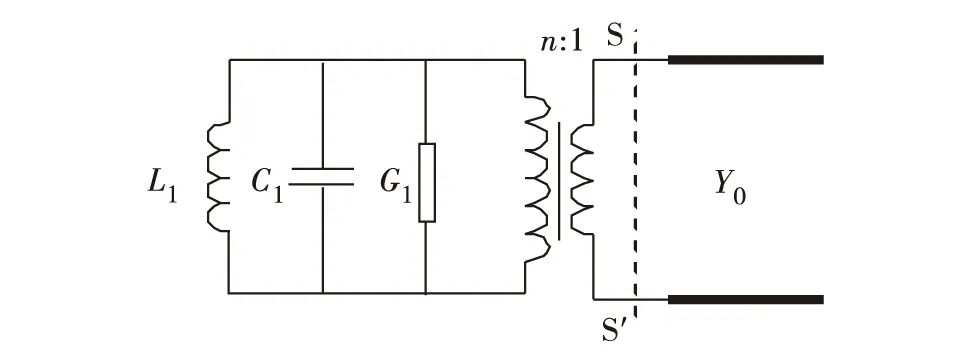
图3 单波导与同轴腔耦合等效电路Fig.3 Equivalent circuit of single waveguide and coaxial cavity coupling system
在图3中距离失谐短路面SS′为1/4波长处放置端面短路板,则此时波导被截成矩形波导腔,波导腔的主模为TE101,这时的波导不能仅看作单纯的传输系统,耦合系统工作于双腔耦合状态.耦合系统等效电路如图4,端面短路板处对应的并联谐振参考面用等效并联谐振回路表示,等效电感、电容和电导分别是L2、C2和G2. 同轴腔的等效电感、电容和电导分别是L1、C1和G1,同轴腔与波导的耦合等效为n∶1的理想变压器.同轴腔TM110模和波导腔TE101模固有品质因数分别为Q1和Q2,本征频率分别为f1和f2. 由1/4 波长变换器特性可知,端面短路板处并联谐振参考面的总导纳Y2经变换到SS′参考面的总导纳Y2′=Y02/Y2. 其中,Y2′经n∶1变压器变换到同轴腔内的导纳Y2″=Y2′/n2=Y02/(n2Y2). 从SS′参考面向同轴腔看进去的总输入导纳为
(3)
其中,T=1+jQ2(f/f2-f2/f).当耦合系统并联谐振时,式(3)的归一化导纳虚部为0,可以得到2个并联谐振频率解,分别对应0模和π模频率,两模式电场在同轴腔结合面的两个方向上分别相同和相反.
但是,当波导上的同轴探针接匹配负载强耦合时,矩形波导腔失谐,此时端面短路的矩形波导只起传输信号和滤波作用,耦合输出信号频率为圆柱形同轴腔TM110模的本征频率f1.

图4 端面短路波导与同轴腔耦合等效电路Fig.4 Equivalent circuit of the system coupled with shorted end-face waveguide and coaxial cavity coupling system
3 双波导与同轴腔耦合等效电路
以上考虑的是圆柱形同轴腔与一个波导耦合的情形,而从图2中的TM110模电场强度分布图可见,端口1和2对应的2个波导都与同轴腔耦合.由以上分析可知,当波导上的同轴探针接匹配负载强耦合时,波导只能看作为一个传输结构;当波导上的同轴探针耦合度非常低时,端面短路的矩型波导可看作为矩形波导腔,则弱耦合下的模式耦合关系可利用多腔等效谐振回路来分析.为便于分析,用等效串联谐振电路来表示耦合关系,当两个对称波导的等效参数相同时,建立的等效电路如图5.
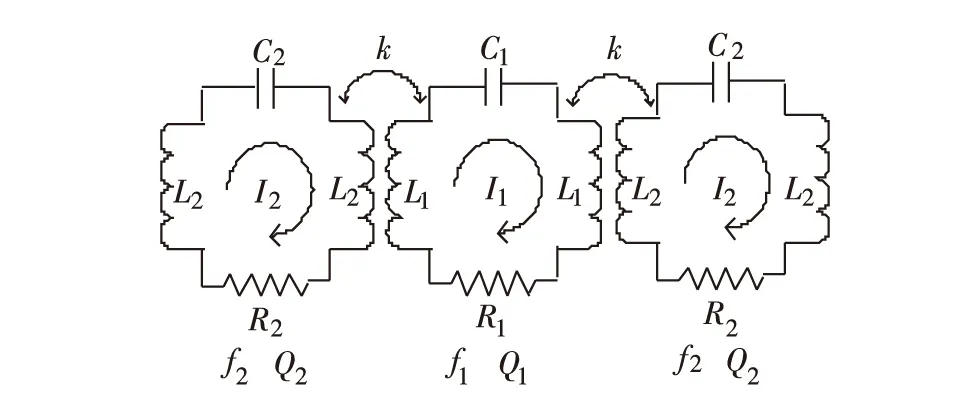
图5 多腔耦合系统等效电路Fig.5 Equivalent circuit of multi-cavity coupling system
图5中k为腔间的耦合系数,L1、C1和R1分别表示圆柱形同轴腔等效电感、电容和电阻,L2、C2和R2分别表示矩形波导腔等效电感、电容和电阻,f1和f2分别表示圆柱形同轴腔TM110模和波导腔TE101模本征频率;Q1和Q2分别表示它们的固有品质因数.根据基尔霍夫定律求解谐振回路可得如下方程[14-15]
(4)
求解方程(4)可得到谐振频率f的3个解,分别对应π/2模频率为f1, 以及0模和π模的谐振频率fa和fb.
(5)
(6)
其中,m=(4-2k2)f12f22.fa、fb与f1的频率间隔取决于耦合系数k的大小.
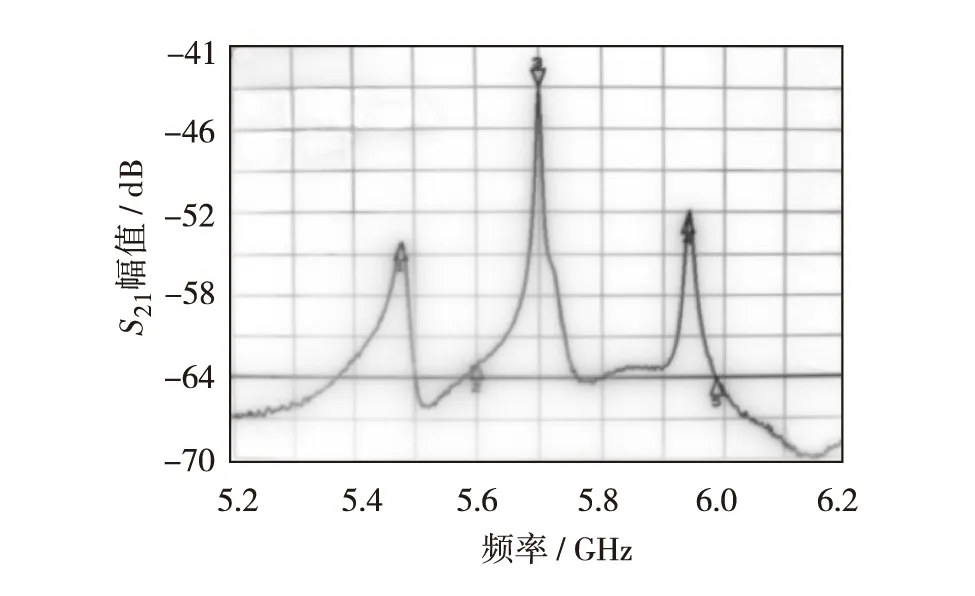
图6 弱耦合系统正向传输系数S21测量曲线Fig.6 Forward transmission coefficient S21 frequency curve for weak coupling system
4 实验结果
使用矢量网络分析器对同轴腔加载波导滤波器系统进行测试,在波导中心处插入同轴探针耦合输出信号,当同轴探针插入深度为1mm时,图2横向对波导对应的端口1和2间的正向传输系数S21曲线如图6,可看出3个谐振频率点,中间谐振频率5.711GHz对应同轴腔TM110模本征频率,两边分别为0模和π模对应的谐振频率点,3个谐振点的频率间隔随探针插入深度改变而变化,即随耦合系数大小而变化.
当同轴探针插入较深5mm时,系统处于强耦合状态时,多腔谐振条件破坏,只存在1个固有谐振频率点.此时1号和2号波导端口间的正向传输系数S21曲线如图7.可看出此时只剩下5.711 GHz这一个谐振频率点,说明矩形波导腔失谐,波导起滤波及耦合输出信号作用.
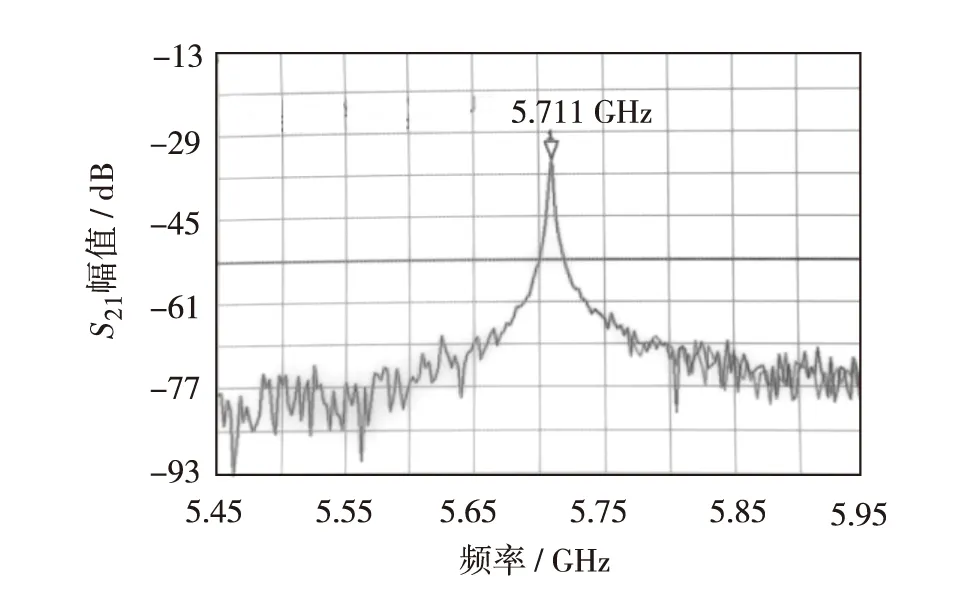
图7 强耦合系统正向传输系数S21测量曲线Fig.7 Forward transmission coefficient S21 frequency curve for strong coupling system
结 语
以同轴腔加载波导滤波器系统为研究对象,分别建立单个波导以及双波导与同轴腔耦合等效电路模型,在波导端面短路,且同轴探针弱耦合状态下,通过求解回路方程组,得到3个谐振频率点,分别对应π/2模、0模以及π模.同轴探针强耦合状态下,仅存在1个谐振频率点,波导只起传输信号及滤波作用.实验测量得到的S21参数与理论分析一致.研究结果对于同轴腔高次模耦合输出系统的设计具有一定的借鉴意义.
/ References:
[1] Chen F C,Qiu J M,Wong S W,et al.Dual-band coaxial cavity bandpass filter with helical feeding structure and mixed coupling[J].IEEE Microwave and Wireless Components Letters,2015,25(1):31-33.
[2] Dong Yuhe,Liu Tianda,Cao Jing,et al.Bandwidth simulation of coaxial cavity coupled with waveguide filter by transmission method[C]// The 15th IEEE Inter-national Vacuum Electronics Conference.Monterey (USA):IEEE Press,2014:351-352.
[3] Xie Xingjuan,Huang Chuanlu,Dong Yuhe,et al.Output circuit design for double gap coaxial cavity loaded with waveguide filter[J].High Power Laser and Particle Beams,2012,24(8):1925-1930.(in Chinese) 谢兴娟,黄传禄,董玉和,等.双间隙同轴腔加载波导滤波器输出回路设计[J].强激光与粒子束,2012,24(8):1925-1930.
[4] Dong Yuhe,Liu Yongxia,Zhu Min.Klystron output circuit of high order transverse magnetic mode in coaxial cavity loaded with waveguide filter[J].Journal of Electronics & Information Technology,2013,35(5):1267-1270.(in Chinese) 董玉和,刘永霞,朱 敏.速调管输出腔高阶横磁模式加载波导滤波器输出回路[J].电子与信息学报,2013,35(5):1267-1270.
[5] Zhang Rui,Wang Yong.Study on the two-port output system for an L-band 10 MW coaxial cavity multi-beam klystron[J].Journal of Electronics & Information Technology,2012,34(9):2282-2286.(in Chinese) 张 瑞,王 勇.L波段10 MW同轴腔多注速调管双端口输出系统的研究[J].电子与信息学报,2012,34(9):2282-2286.
[6] Zhao Lei,Gao Xingshun,Hu Xiaofang.Beam position and phase measurement system for the proton accelerator in ADS[J].IEEE Transactions on Nuclear Science,2014,61(1):538-545.
[7] Shin Seunghwan,Wendt M.Design studies for a high resolution cold cavity beam position monitor[J].IEEE Transactions on Nuclear Science,2010,57(4):2159-2166.
[8] Slater M,Adolphsen C,Arnold R,et al.Cavity BPM system tests for the ILC energy spectrometer[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment,2008,592(3):201-217.
[9] Walston S,Boogert S,Chung C,et al.Performance of a high resolution cavity beam position monitor system[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment,2007,578(1):1-22.
[10] Su Jiahang,Du Yingchao,Hua Jianfei,et al.Design and cold test of a rectangular cavity beam position monitor[J].Chinese Physics C,2013,37(1):107-112.
[11] Li Jisan.Wang Yong,Liu Wenxin.Resonant frequency computation of waveguide-loaded cavity with boundary element method[J].High Power Laser and Particle Beams,2012,24(1):3-4.(in Chinese) 李纪三,王 勇,刘文鑫.计算波导加载谐振腔谐振频率的新方法[J].强激光与粒子束,2012,24(1):3-4.
[12] Han Huipeng,Wang Yong,Zhang Rui.Parasitic mode-suppression in TM310-mode coaxial resonator of multiple-beam klystron[J].Chinese Journal of Vacuum Science and Technology,2011,31(4):413-418.(in Chinese) 韩慧鹏,王 勇,张 瑞.多注速调管TM310模同轴谐振腔杂模抑制的研究[J].真空科学与技术学报,2011,31(4):413-418.
[13] Zhang Shichang.Analysis of equivalent circuit for radial coupling multi-cavity resonators[J].Journal of Electronics & Information Technology,2004,26(4):640-644.(in Chinese) 张世昌.多腔径向耦合输出系统的等效电路分析[J].电子与信息学报,2004,26(4):640-644.
[14] Shi Jiaru,Zheng Shuxin,Chen Huaibi.Calculating field distribution of a linear accelerator using equivalent circuit model[J].High Energy Physics and Nuclear Physics,2006,30(7):699-703.(in Chinese) 施嘉儒,郑曙昕,陈怀璧.耦合腔链等效电路模型计算加速管场分布[J].高能物理与核物理,2006,30(7):699-703.
[15] Xu Jiaming,Chen Lin,Zang Xiaofei,et al.Triple-channel terahertz filter based on mode coupling of cavities resonance system[J].Applied Physics Letters,2013,103(16):1116-1120.
【中文责编:英 子;英文责编:雨 辰】
Equivalent circuit model of waveguide filter and experimental research
Chu Jianhua1,2†, Qian Rongrong2, and Wang Chuanqi2
1) Depcotment of Mechanical and Electrical Engineering, Suzhou Institute of Industrial Technology, Suzhou 215104, P.R.China 2) Hefei Institute of Physical Science, Chinese Academy of Sciences, Hefei 230031, P.R.China
We establish an equivalent circuit model to analyze the coaxial cavity coupled with waveguide filter. By solving the circuit equations, we derive three resonant frequencies of π/2 mode, zero mode and π mode in the case of weak coupling. The resonant frequency internals for three modes depend on the coupling coefficient. There is only one resonant frequency in the case of strong coupling. We test the forward transmission coefficient of waveguide filter system. We obtain three resonant frequencies for weak coupling case and one resonant frequency for strong coupling case in experimental measurements. The results agree well with theoretical predictions.
microwave technique; waveguide; coaxial cavity; waveguide filter; equivalent circuit model; high order mode; coupling coefficient
:Chu Jianhua,Qian Rongrong,Wang Chuanqi.Equivalent circuit model of waveguide filter and experimental research[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 183-187.(in Chinese)
TN 61;O 441
A
10.3724/SP.J.1249.2015.02183
国家自然科学基金资助项目(61005064);苏州市应用基础研究计划资助项目(SYG201438)
储建华(1982—),男(汉族),安徽省安庆市人,苏州工业职业技术学院副研究员、博士.E-mail: hamigua878@163.com
Received:2014-06-28;Revised:2015-01-23;Accepted:2015-03-02
Foundation:National Natural Science Foundation of China (61005064); Applied Basic Research Programs of Suzhou (SYG201438)
† Corresponding author:Associate professor Chu Jianhua. E-mail: hamigua878@163.com
引 文:储建华,钱荣荣,王传齐.波导滤波器的等效电路模型及实验研究[J]. 深圳大学学报理工版,2015,32(2):183-187.
