基于矢量理论分束器设计方法及其机理的探讨
2015-04-27黄海漩阮双琛黄燕燕
黄海漩,徐 平,阮双琛,杨 拓,袁 霞,黄燕燕
深圳大学电子科学与技术学院,深圳 518060

【光电工程 / Optoelectronic Engineering】
基于矢量理论分束器设计方法及其机理的探讨
黄海漩,徐 平,阮双琛,杨 拓,袁 霞,黄燕燕
深圳大学电子科学与技术学院,深圳 518060
分析以矢量理论求解二元简单周期结构衍射效率的原理和过程,探讨一种高性能偶数分束器设计方法,通过自编程序在太赫兹波段获得二元结构偶数分束器,有效抑制了零级衍射,突破传统标量方法设计的局限性.探讨了该设计方法利用共振效应及倏逝波传播效应抑制零级衍射光,以及将能量分配到其他非零级次上的物理机理.
电磁波物理;亚波长;二元结构;偶数分束器;严格耦合波法;抑制零级衍射
高性能偶数型分束器[1-3]已在光纤光栅线性啁啾相位掩膜的制作、光刻机光学系统分束和数字全息光学系统去噪等高消零级衍射要求的特殊场合广泛应用.与奇数型分束器[4-10]相比,偶数分束器由于必须满足消除零级噪声条件下的高衍射效率和高光强均匀性要求,其设计优化过程相对奇数型分束器更为复杂和困难,且制作工艺要求高,制作难度大.目前传统偶数分束器研究主要基于标量理论设计的复周期Dammann结构[11-12],其相位突变点较多、线条精度跨度大,制作精度要求较高,实际制作时很难保证较好的零级抑制效果和高衍射效率.此外,传统标量设计理论对于二元简单周期结构的分析表明,零级衍射始终无法消除,因而未能实现偶数分束.目前国内外尚未见基于二元简单周期结构,实现消零级、高衍射效率和高均匀性偶数分束的相关报道.
本研究基于二元光学衍射设计理论及其应用[13-22],通过分析矢量理论求解二元简单周期结构衍射效率的原理和过程,探讨一种高性能偶数分束器设计方法,采用自编程序在太赫兹波段获得了二元结构偶数分束器,有效抑制了零级衍射,突破传统标量方法设计的局限性.深入探究该方法物理机理,认为其实质是:通过设计亚波长二元结构的参数,使零级衍射光发生共振效应并形成在分束器表面传播的倏逝波而无法透射,成功抑制了零级衍射.
1 设计理论
采用的亚波长二元结构如图1,其折射率在y方向(垂直纸面向外)上均匀分布,在x方向上周期分布,光栅脊宽为a,周期为d,光栅深度为h1,占空比f=a/d,基底介质厚度为h2.在z方向上光栅区域划分为4个水平层:z<0为入射介质层,其折射率为n1;0
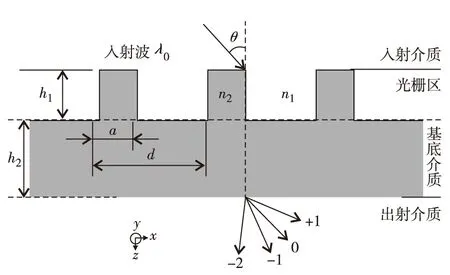
图1 亚波长二元周期结构模型Fig. 1 Model of a subwavelength binary structure
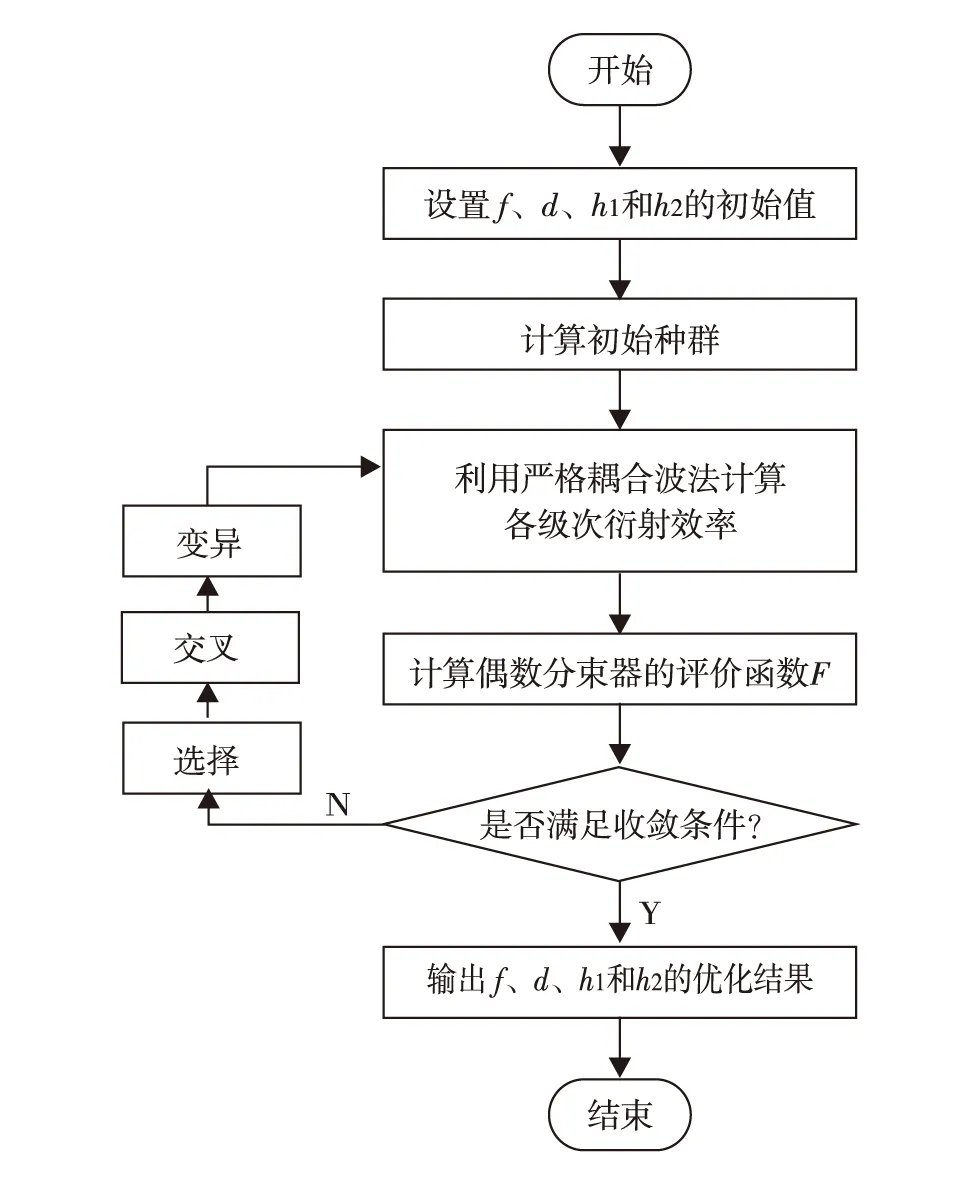
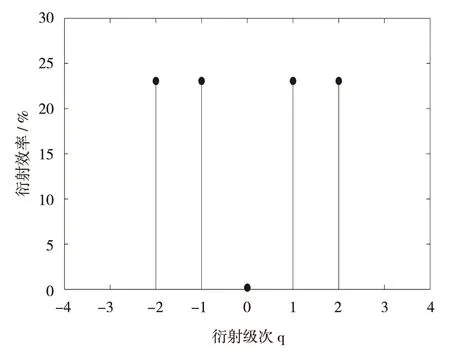
图1中,波长为λ0的TE平面波以θ角入射到分束数为N=2L(L= 1,2,…,n,其中n∈N)的光栅.若垂直入射,光栅周期d取值为Lλ0/n1 以TE偏振入射为例,阐述严格耦合波法求解过程.对于图1的周期矩形光栅,其光栅层沿x方向的介电常数具有周期性,即相对介电常数εr(x)=εr(x+d),用傅里叶级数展开形式表示为 (1) 其中,傅里叶系数为 (2) 入射波为TE波时,入射波的电场仅存在y分量,入射介质层1、基底层3和出射介质层4的电场解的表达式可根据瑞利展开式展开,光栅层2的电场和磁场可由傅里叶级数展开,分别表示为 E1,y=exp[-jk0n1(xsinθ+zcosθ)]+ (3) h1 z>h1+h2(5) 0 (7) 其中,Rq为反射到入射介质层1的q级衍射波的归一化电场振幅;Tq为透射到出射层4的q级衍射波的归一化电场振幅;R3q和T3q分别是在基底层3中反射和透射波的电场振幅;Syq和Uxq分别为光栅层2的q级衍射波的电场振幅和磁场振幅;k0=2π/λ0,为入射光在真空中的波数,λ0为入射波在真空中的波长;kxq为第q级衍射波矢的x分量,由Floquet条件决定 kxq=k0x-qK= (8) 其中,K=2π/d;k1,zq、k3,zq和k4,zq分别为入射区域(入射介质层1)、基底层3和出射层4第q级衍射波矢的z分量,即q次谐波场在介质1、3和4中的波矢分量,满足关系 (9) 其中,l=1,3,4. 将各区电磁场解的表达式(3)至式(7)和介电常数的傅里叶展开式(1)代入麦克斯韦方程组,推导得到耦合波方程 (10) 方程(10)为无穷维方程,故需截断为有限维方程组再进行数值求解.在入射层1与光栅层2、光栅层2与基底层3、基底层3与出射层4边界上运用电磁场边界条件,采用特征值法结合高斯消去法对方程(10)进行数值求解,得到各级反射波振幅系数Rq与透射波的振幅系数Tq. 反射区及透射区的各级衍射波的衍射效率ηRq和ηTq为 (11) 从而得到各级透射波的衍射效率Pq=ηTq(q为衍射级次,q=0,±1,±2,…,±L)的数值解[25].该数值解与光栅的占空比f、周期d、槽深h1和基底厚度h2等结构参数相关,因此,各级透射波衍射效率Pq(q=-2,-1,0,1)可由严格耦合波法通过光栅结构参数(f、d、h1和h2)进行数值求解. 偶数分束器的设计目标是以4个光栅结构参数为自变量,控制各级透射波的衍射效率,实现零级衍射效率最小、各非零级次衍射效率之和最大且均匀分布,即考虑去零级衍射级次、各非零级次衍射效率均匀性和总衍射效率3个因素.因此,设定评价函数为 (12) 其中,2L为偶数分束数;α、β、μ和ν为权重因子,在[0,1]取值, 且满足α+β+μ+ν=1,可根据不同设计要求设置;P与U分别为各非零衍射级衍射效率之和(总衍射效率)及其均匀性误差[24],分别为 (13) U=(Pmax-Pmin)/(Pmax+Pmin) (14) 这里,Pmax和Pmin分别为2L个非零衍射级次中的最大衍射效率和最小衍射效率. 式(12)第1项和第2项考虑了各分束衍射效率及其均匀性,第3项考虑了总衍射效率,第4项考虑了零级衍射效率的抑制.因此,设计的实质即求一组二元周期结构参数(f、d、h1和h2),使评价函数F最小.由于评价函数中的各级衍射效率Pq是一个多变量函数,且只有数值解,不能表达为上述参数的显函数,而遗传算法具有跳出局部极值点的机制,特别适合解决多变量、离散变量优化问题[26-27],因此,本研究将该法应用于式(12)中评价函数F的优化.首先,设定f、d、h1和h2的初始值,产生初始种群;然后,计算各级衍射效率和评价函数F. 若不满足收敛条件,则对种群进行选择、交叉和变异操作.重新计算评价函数并进行收敛性条件判断.反复进行这一过程直到收敛性条件满足后,输出优化参数f、d、h1和h2的值,求出分束器结构参数的最优值.优化设计流程如图2. 图2 遗传算法与严格耦合波法相结合优化亚波长矩形周期光栅结构参数流程图Fig.2 Flow chart of grating parameters optimization by combining GA with RCWA 设定优化初始条件为:分束数N=4,入射光频率为太赫兹波段(2.52THz);TE偏振垂直入射;入射介质为空气,其折射率n1=1.00;光栅介质材料为对太赫兹波段透明的高阻硅,其折射率n2=3.42. 根据运算,最优设计结果如图3和表1. 图3 基于高阻硅的太赫兹4分束器各级输出衍射效率分布图Fig.3 Distributions of the efficiency of each diffraction order of a silicon-based terahertz even splitter 表1 太赫兹偶数分束器设计结果 Table 1 Results of a designed terahertz even beam splitter d/μmh1/μmh2/μmfa/μm最小特征尺寸/μm各级衍射效率分布/%P-2P-1P0P+1P+2P/%104U/%269.7175.218.10.409110.2110.223.058623.05890.192023.058923.058692.2306.51 由图3和表1可知,用波长为118.83 μm(工作频率为2.52 THz)的TE偏振太赫兹波垂直入射本研究设计的亚波长二元结构分束器,总体分束衍射效率可达92.230%,零级衍射效率抑制在0.192%以下,均匀性误差控制在6.51×10-6以内,能量均匀地分配到±1和±2级,其衍射效率高于文献[11-12]中报道的80%、60%~83%和90%,相对均匀性误差优于所报道的5.7×10-5~3.2×10-4.太赫兹波偶数分束的衍射效率、均匀性误差和零级抑制等性能指标理想.由于使用了二元简单周期结构,大大降低了制作难度,易于实现. 本研究设计结果是传统标量衍射理论所无法实现的.原因可能在于: 1)在设计方法方面,采用亚波长二元结构,该结构对光波偏振方向敏感且衍射效率高.另外,通过综合运用严格耦合波精确描述电磁波在亚波长结构中电场分量与磁场分量及其各个标量分量直接耦合作用及边界条件对电磁场的强烈的耦合作用,结合有效的全局优化算法——遗传算法,对可能存在的最优解进行全局搜索,提高了寻得最优结构参数的可能性; 2)在物理机理方面,利用亚波长结构的特性,使零级衍射光在亚波长结构内发生共振效应并形成在分束器表面传播的倏逝波而无法透射,在实现抑制零级衍射级的同时将更多的能量分配到其他非零级次上.而传统标量设计理论仅考虑电场的一个分量,无法讨论偏振属性,不适合分析亚波长结构.因此,这正是本研究方法突破传统标量理论分束器设计局限性的根本原因. 采用共振效应及倏逝波传播效应来解释抑制零级衍射光及将能量分配到其他非零级次上的物理机制,是我们初步探讨的结果,由于该结构属于多层介质膜亚波长光栅,耦合过程相对复杂,或许可利用光波的模式匹配理论,通过考虑高级次子波与波导的模式耦合作用,以揭示共振机制.受篇幅所限,在此从略. 通过分析矢量理论求解二元简单周期结构衍射效率的原理和过程,本研究探讨了一种高性能偶数分束器设计方法,并采用自编程序在太赫兹波段获得了二元结构偶数分束器,可有效抑制零级衍射,并突破传统标量方法设计的局限性.理论分析结果表明,该亚波长二元结构分束器采用波长为118.83 μm的TE偏振太赫兹波垂直入射,能量均匀地分配到±1和±2级,偶数分束的衍射效率、零级抑制及均匀性指标都非常理想.二元简单周期结构的应用大大降低了制作难度,使该设计易于实现.深入探究本研究设计方法突破传统标量理论局限性的物理机理,其原因在于:通过调整光栅结构参数利用亚波长二元结构的特性,使零级衍射光在亚波长结构内发生共振效应并形成在分束器表面传播的倏逝波而无法透射,在实现抑制零级衍射级的同时将更多的能量分配到其他非零级次上. 本研究设计结果突破了简单结构下的高衍射效率、高均匀性的消零级衍射偶数分束实现问题,可应用于光纤光栅线性啁啾相位掩膜的制作、光刻机光学系统分束和数字全息光学系统去噪等高消零级衍射要求等领域. / References: [1] Li Jingzhen.Handbook of optics[M].Xi’an:Shanxi Science and Technology Press of China,2010:1070.(in Chinese) 李景镇.光学手册[M].西安:陕西科学技术出版社,2010:1070. [2] Liu Quan,Wu Jianhong,Yang Weipeng,et al.Fabrication of linearly chirped phase mask[J].Chinese Journal of Lasers,2009,36(3):677-682.(in Chinese) 刘 全,吴建宏,杨卫鹏,等.线性啁啾相位掩模的研制[J].中国激光,2009,36(3):677-682. [3] Chen Shaowu.Analysis on tolerance for fabrication error of phase mask for UV written fiber Bragg grating[J].Journal of Optoelectronics·Laser,1998,9(6):469-471.(in Chinese) 陈少武.紫外写入光纤光栅用亚μm相位掩模板制作误差容限分析[J].光电子·激光,1998,9(6):469-471. [4] Philippe L,Jerome H,Pierre C,et al.A transmission polarizing beam splitter grating[J].Journal of Optics A:Pure Applied Optics,1999,1(2):215-219. [5] Zheng Jiangjun,Zhou Changhe,Feng Jijun,et al.Polarizing beam splitter of two-layer dielectric rectangular transmission gratings in Littrow mounting[J].Optics Communications,2009,282(15):3069-3075. [6] Wang Bo,Chen Li,Lei Lei,et al.Metal-based phase grating for high-efficiency polarizing beam splitter [J].Optics Communications,2013,296(1):149-152. [7] Guan Xiaowei, Wu Hao, Shi Yaocheng, et al. Extremely small polarization beam splitter based on a multimode interference coupler with a silicon hybrid plasmonic waveguide[J].Optics Letters,2014,39(2):259-262. [8] Guo Lingwei,Ma Jianyong.Broad band beam splitter based on the double-groove fused silica grating[J].Optik,2014,125(1):232-234. [9] Hsu J H,Lee C H,Chen R S,et al.A high-efficiency multi-beam splitter for optical pickups using ultra-precision manufacturing[J].Microelectronic Engineering,2014,113:74-79. [10] Feng Jijun,Zhou Changhe,Wang Bo,et al.Three-port beam splitter of a binary fused-silica grating[J].Applied Optics,2008,47(35):6638-6643. [11] Herzig H P.Micro-optics:elements,systems and applications[M].Boca Raton(USA):Taylor & Francis Ltd,1997. [12] Zhou Changhe,Bi Qunyu.Isocandela grating to eliminate the zero-order spectra[P]. China: ZL200710171391.3,2008-05-28.(in Chinese) 周常河,毕群玉.消除零级谱点的等光强光栅[P].中国:ZL200710171391.3,2008-05-28. [13] Huang Haixuan,Ruan Shuangchen,Yang Tuo, et al.Novel even beam splitters based on subwavelength binary simple periodic rectangular structure[J/OL].Nano-Micro Letters,2015,Doi:10.1007/s40820-015-0031-y.(2015-02-13).http://link.springer.com/article/10.1007%2Fs40820-015-0031-y. [14] Xu Ping,Huang Yanyan,Su Zhijie,et al.Research of micro-prism distribution on the bottom surface of the small-size integrated light guide plate[J].Optics Express,2015,23(4):4887-4896. [15] Xu Ping,Huang Yanyan,Zhang Xulin,et al.Integrated micro-optical light guide plate[J].Optics Express,2013,21(17):20159-20170. [16] Xu Ping,Huang Haixuan,Wang Kai,et al.Realization of optical perfect shuffle with microoptical array element[J].Optics Express,2007,15(3):809-816. [17] Xu Ping,Huang Yanyan,Su Zhijie,et al.Algorithm research on microstructure distribution on the bottom surface of an integrated micro-optical light guide plate[J].Applied Optics,2014,53(7):1322-1327. [18] Xu Ping, Hong Chunquan, Sun Zhilong, et al. Integrated zigzag Vander Lugt correlators incorporating an optimal trade-off synthetic discriminant filter for invariant pattern recognition[J].Optics Communications,2014,315(15):97-102. [19] Xu Ping,Li Jingzhen.The even device fabricated by the deep etched binary optics technology for the exposure system of the quasi-molecule laser[J].Science in China:Series E,2002,45(1):1-9.(in Chinese) 徐 平,李景镇.深蚀刻二元光学技术制作准分子曝光系统均匀器[J].中国科学:E辑,2002,45(1):1-9. [20] Xu Ping,Zhou Xiang,Zhang Xiaochun,et al.Optical perfect shuffle interconnection using computer-generated blazed grating array[J].Optical Review,1995,2(5):362-365. [21] Huang Haixuan,Xu Ping,Yang Jing,et al.Method of state code matrixes in the realization of optical switching using perfect shuffle[J].Optics Communications,2009,282(21):4198-4202. [22] Xu Ping,Tang Jiyue,Guo Lyurong,et al.Deep etch binary optics element[J].Acta Optica Sinica,1996,16(12):1796-1801.(in Chinese) 徐 平,唐继跃,郭履容,等.深蚀刻二元光学元件[J].光子学报,1996,16(12):1796-1801. [23] Yan Shuhua.Design of diffraction microoptics[M].Beijing:National Defense Industry Press of China,2011:269-272.(in Chinese) 颜树华.衍射微光学设计[M].北京:国防工业出版社,2011:269-272. [24] Marciante J R,Farmiga N O,Hirsh J I,et al.Optical measurement of depth and duty cycle for binary diffraction gratings with sub-wavelength features[J].Applied Optics,2003,42(16):3234-3240. [25] Moharam M G,Grann E B,Pommet D A,et al.Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J].Journal of the Optical Society of America A:Optics,Image Science,and Vision,1995,12(5):1068-1076. [26] Cormier G,Boudreau R,Thériault S,et al.Real-coded genetic algorithm for Bragg grating parameter synthesis[J].Journal of the Optical Society America B:Optical Physics,2001,18(12):1771-1776. [27] Goldberg E.Genetic algorithm in search,optimization and machine learning[M].New York:Addison-Wesley Publishing Company,1987. 【中文责编:英 子;英文责编:子 兰】 A method to design beam-splitters based on vectorial theory and discussion on its physical mechanism Huang Haixuan, Xu Ping†, Ruan Shuangchen, Yang Tuo, Yuan Xia, and Huang Yanyan College of Electronic Science and Technology, Shenzhen University, Shenzhen 518060, P.R.China This paper analyses the principle and process to solve the diffraction efficiency of gratings with binary simple period structures by applying vectorial theory and explores a method to design a high-performance even-beam splitter. By programming, we obtain an even splitter with a binary structure in the Terahertz range. Thus, the zero-order diffraction is suppressed effectively, and it breaks the design limit of the traditional scalar theory. In addition, we discuss the physical mechanism of the method to suppress the zero-order diffraction by resolving the energy to the non-zero-order diffractions due to the resonance effect and the evanescent wave propagation effects. electromagnetic wave physics; subwavelength; binary structure; even beam splitter; rigorous couple-wave; zero-order diffraction suppress :Huang Haixuan,Xu Ping,Ruan Shuangchen,et al.A method to design beam-splitters based on vectorial theory and discussion on its physical mechanism[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 172-177.(in Chinese) TM 154.4 A 10.3724/SP.J.1249.2015.02172 国家自然科学基金资助项目(61275167)、深圳市基础研究计划资助项目(JCYJ20130329103020637) 黄海漩(1981—),男(汉族),广东省海丰县人,深圳大学博士研究生.E-mail:hhx@szu.edu.cn Received:2015-01-26;Accepted:2015-03-03 Foundation:National Natural Science Foundation of China (61275167); Basic Research Project of Shenzhen (JCYJ20130329103 020637) † Corresponding author:Professor Xu Ping.E-mail: xuping@szu.edu.cn 引 文:黄海漩,徐 平,阮双琛,等.基于矢量理论分束器设计方法及其机理的探讨[J]. 深圳大学学报理工版,2015,32(2):172-177.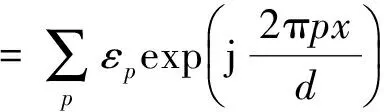
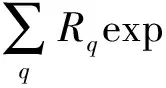
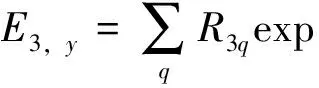
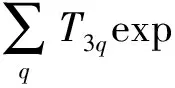
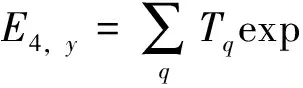
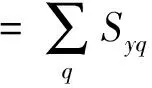
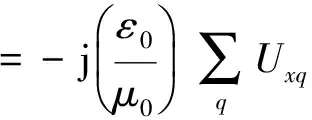
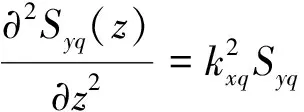
2 优化设计方法及结果

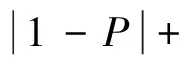

3 物理机理分析
结 语
