让数学基本思想根植学生心中

黄健哲

(三明市梅列区陈大中心小学，福建 三明 365009)

美国数学家哈尔莫斯说:“数学的核心应该是越过这些表面知识的内在问题、思想和方法，并且问题是数学的心脏，思想是数学的灵魂，方法是数学的行为。”［1］小学是学生数学学习的起始阶段，教师应该借助新课程改革春风，把握“两基”变“四基”契机，在数学教学中渗透数学基本思想，让其植根于学生心中，为学生优化知识结构、提升数学素养增动力，为他们当前学习乃至今后发展添活力。

一、精挑细选，让渗透更加求真

“两基”变“四基”后，“数学基本思想”走进了数学课堂，走进了学生学习。但仔细审视之下，笔者却发现了两种“极端”:一是“言必说思想，语必话方法”式灌输;二是“穿‘四基’鞋子，走‘两基’老路”式漠视。于是，笔者精挑细选教学内容，让渗透更加“求真”:使“掌握基本知识”“训练基本技能”成为“领悟基本思想”和“积累基本活动经验”［2］载体，使“基本思想”成为数学教学的精髓，使“基本活动”成为数学教学的形式;将“领悟基本思想”“掌握基本知识”“训练基本技能”融入“积累基本活动经验”的过程，让学生在“知识学习、能力训练、思维发展三统一”中学会数学思考、品味数学真谛和提高数学素养。

每学期初，笔者与同事们认真学习“数学基本思想”相关理论，明确适合小学阶段教学的数学思想;集中时间领会“课标”的精神，理清教材的脉络，分析学生学情，建立和完善《数学基本思想与小学数学知识“结合点”排查表》(见表1)，对“对应”“假设”“比较”“转化”等17 种数学思想进行了细致、深入的排查，并在教学过程中适时补充，为日常教学渗透数学基本思想提供了导向。

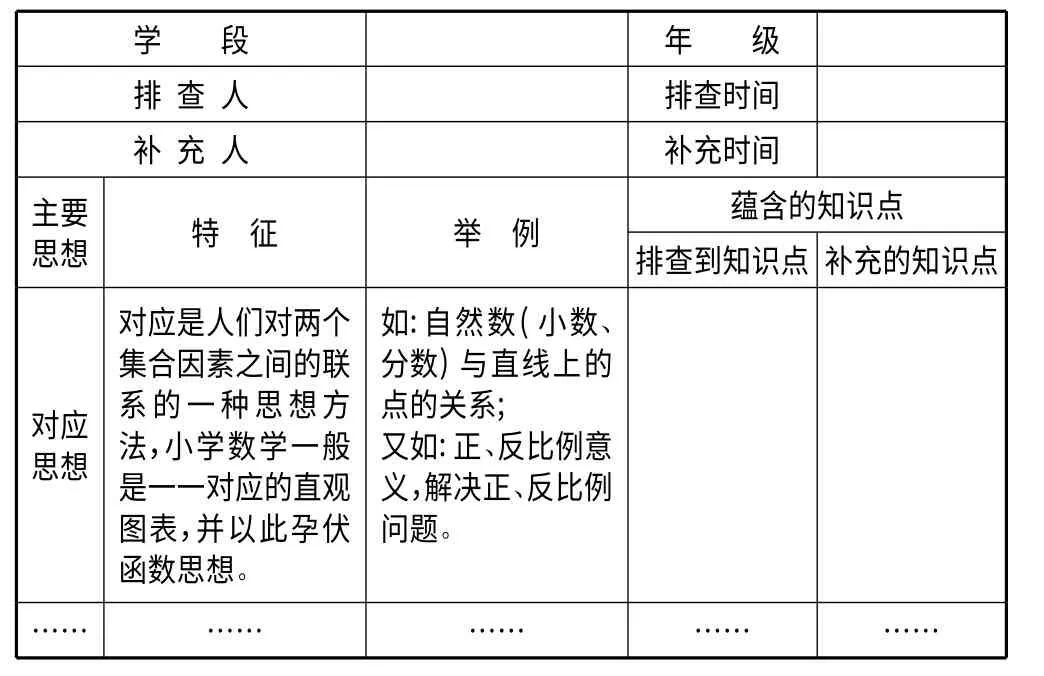
表1 数学基本思想与小学数学知识“结合点”排查表

实施过程中，笔者与同事们加强理论学习，加强集体备课，加强示范教学，加强专题研讨，加强总结推广，促使数学教学渗透基本思想的思路更加明确，更加真实，数学的“科学性”“价值性”和“实用性”日益显现，课堂的“数学味”“吸引力”和“人文化”日益浓厚。

二、精耕细耘，让渗透更加务实

“两基”变“四基”后，“数学基本思想”成为了关注对象，成为了教学热点。为此，笔者精耕细耘教学过程，让渗透更加“务实”:积极挖掘教学内容中蕴涵的“数学基本思想”，并在教学目标中明确，在教学预案中体现，在知识形成中渗透，在巩固练习中内化，在解决问题中深化，在归纳总结时提升，使之成为学生加强数学理解、发展数学思维和增强数学应用的增长极。

例如，教学《植树问题》时，笔者将“利用‘数形结合’思想解决‘简单植树问题’”纳入学习目标，并设计了以下环节引导学生主动参与学习:一是通过贴近生活、富有情趣的游戏——“手指数与间隔数”导入新课，让学生“玩中学”“做中思”，直观感受数学问题，初步感知“数形结合”思想。二是通过化繁为简、重组优化的例题——“六一节快到了，学校准备在校门口50 米长的水泥路的一边摆上鲜花，(1)如果每隔10 米摆一盆(两端要摆)。一共要摆多少盆?(2)如果每隔10 米摆一盆(两端不摆)。一共要摆多少盆?(3)“学校准备在圆形花坛的周围也摆上鲜花。花坛的周长也是60 米，如果每隔10 米摆一盆，一共要摆多少盆?”推进教学，让学生“大胆猜想”“积极验证”“合理归纳”，概括得出“两端要摆”“两端不摆”“只摆一端”的规律，在“数→形→数的转化中深入探究数学问题，逐步形成“数形结合”思想。三是通过分层次、重创新的巩固练习，让学生“丰富经验”“完善方法”，积极优化解决策略，不断发展“数形结合”思想。综观全程，孩子们在有趣的情境、务实的教学中学习知识、形成技能、领悟思想和积累经验，有效达成了预定的学习目标，取得了事半功倍的学习效果。

再如，教学“长方体的体积”时，笔者通过“这些长方体，谁的体积大?谁的体积小?”导出课题，通过猜想“长方体的体积与什么有关系?应该怎样计算?”引发思考，接着引导学生利用事先准备好材料进行实验，孩子们有的“摆正方体小方块”，有的“切长方体萝卜块”，得出了一大堆数据(见表2):

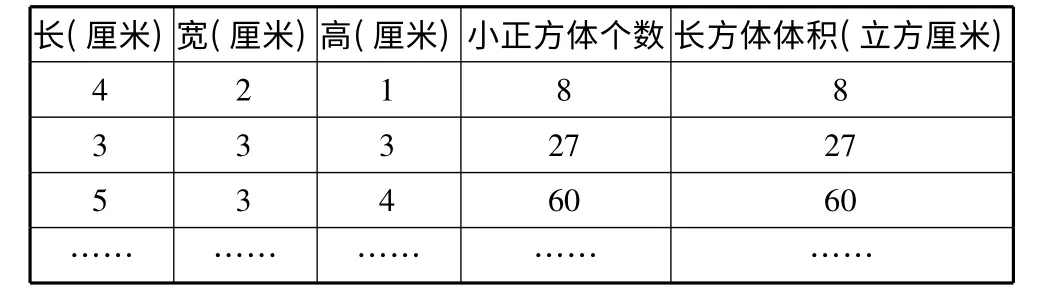
表2 长方体体积

学生观察、思考、交流和讨论后概括得出:长方体的体积=长×宽×高。接着笔者又问:“如果我们用a表示长，b 表示宽，h 表示高，V 表示体积，那么长方体的体积公式该怎样写呢?”经讨论进一步得出:V=abh(板书)，学生在“数形结合”中掌握了“长方体体积”的基本属性，运用起来就得心应手了。

三、精培细育，让渗透更加高效

“两基”变“四基”后，“数学基本思想”升级成教学改革新视角，成为数学教育的突破口。但学生的“数学基本思想”的形成和发展任重道远，需要“师与生互促”和“教与学相长”。所以，笔者精培细育基本思想，让渗透更加“高效”:一是凸显过程性。让学生通过自主探究和合作学习经历数学知识生成、迁移的过程，经历困惑、思考、探索和创新等艰难的心路历程，自主建立数学模型，体验基本思想存在。二是注重系统性。让学生通过系统学习和经常使用数学基本思想来形成解决问题策略的习惯，逐步加深数学基本思想的理解，逐步发展数学基本思想的素养。三是强调反复性。让学生经历“从具体到抽象，从感性到理性”的认知过程，在反复渗透和不断应用中增进理解，在次数增加和体验积淀中实现内化。

例如，教学《鸡兔同笼》时，笔者根据教材编排引导学生学习“列表法”“算术法”和“方程法”，并相应渗透“函数思想”“假设思想”和“代数思想”，让学生在学习知识、形成技能和积累经验的同时，感知、形成和领悟“基本思想”。教学“鸡兔同笼”后，笔者搜集各种相关练习，让学生在问题解决的过程中加深数学理解、提高思维能力和发展基本思想。最后又在“研究性学习”里温习以上方法，还补充介绍了“画图法”“抬脚法”……并相应渗透“数形结合思想”“转化思想”……全程的参与、深入的学习和反复的训练，促使数学基本思想的渗透更加落实、更加有效。

总而言之，小学教学渗透数学基本思想是素质教育的呼唤，是学生发展的需求。教师必须引导学生学习、理解、领悟和运用数学基本思想，让学生在数学基本思想的浸润和滋养中真正做到“人人都能获得良好的数学教育”，真正实现“不同的人在数学上得到不同的发展”。［3］

［1］张素贤.如何在小学课堂中有效渗透数学思想方法［J］.辽宁教育，2013(3).

［2］吴汝萍.从“双基”到“四基”教学策略初探［DB/OL］.枫叶教育网，http://www.fyeedu.net/info/189280-1.html，2014-05-19.

［3］吴正宪.人人获得良好的数学教育［J］.湖北教育，2015(2).