基于统计学方法的工件与车刀后刀面的接触模型构建

江咏平，郑清春，胡亚辉，王雷

(1．天津市先进机电系统设计与智能控制重点实验室，天津 300384;2．天津理工大学，天津 300384)

0 前言

钛合金以其良好的耐热性、耐腐蚀性能，以及优异的力学性能等，广泛应用于航空航天、医疗、化学等工业。然而，作为一种典型的难加工材料，过快的刀具磨损严重制约了其切削加工效率的提高［1］。目前国内外许多学者都对刀具磨损做了研究，李友生、陆丰玮等［2-3］研究了刀具的磨损机制和形式，HARTUNG研究了不同材料刀具的磨损［4］，但是他们基本上都是从宏观角度对刀具磨损进行研究，很少从细观角度进行考虑。车刀后刀面在细观尺度上是粗糙不平的，工件与车刀后刀面实际接触面积只是名义接触面积的一部分，本课题从细观层面进行考量，通过观测车刀后刀面实际表面形貌，分析识别其统计特征参

数，构建刀面表面形貌的细观尺度模型。

1 车刀后刀面表面形貌的数据采集

1．1 实验设备、测量原理及参数设置

1．1．1 实验设备

实验采用的是TR200手持式粗糙度仪，属于接触式测量［5］。仪器各部分名称如图1、图2所示。

1．1．2测量原理

TR200手持式粗糙度仪工作原理框图如图3所示。

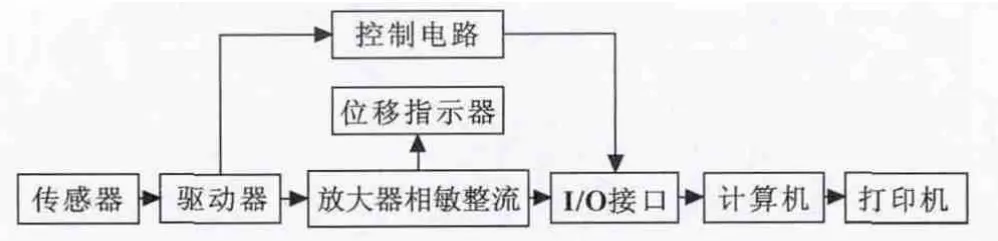
图3 粗糙度仪工作原理框图

其测量原理为:将传感器放在工件被测表面上，由仪器内部的驱动机构带动传感器沿被测表面做等速滑行，传感器通过内置的锐利触针感受被测表面的粗糙度，此时工件被测表面的粗糙度引起触针产生位移，该位移使传感器电感线圈的电感量发生变化，从而在相敏整流器的输出端产生与被测表面粗糙度成比例的模拟信号，该信号经过放大及电平转换之后进入数据采集系统，DSP芯片将采集的数据进行数字滤波和参数计算，测量结果在液晶显示器上读出，也可在打印机上输出，还可以与PC机进行通讯。

1．1．3 参数设置

TR200手持式粗糙度仪的参数设置如表1所示。

表1 参数设置

1．2 车刀试件后刀面表面形貌测量与实验数据采集

粗糙表面可以用微凸体的曲率半径R、高度的标准偏差σ，以及微凸体的概率密度η这3个参数来进行表征［6］。其中，车刀后刀面表面形貌粗糙度均方根值σ就是轮廓均方根偏差Rq，通过测量获得。

取样试件为硬质合金刀具，材料为YG8，试件规格为(10 mm×10 mm×5 mm)。实验中通过将试件与工作台固定，然后调节仪器，将传感器放在工件被测表面上，保持接触。为了提高精度，进行了6次实验;同时在实验的过程中，尽量避开刀具试件表面上明显的缺陷，得到理想的实验数据。后刀面表面形貌数据采集如表2所示。

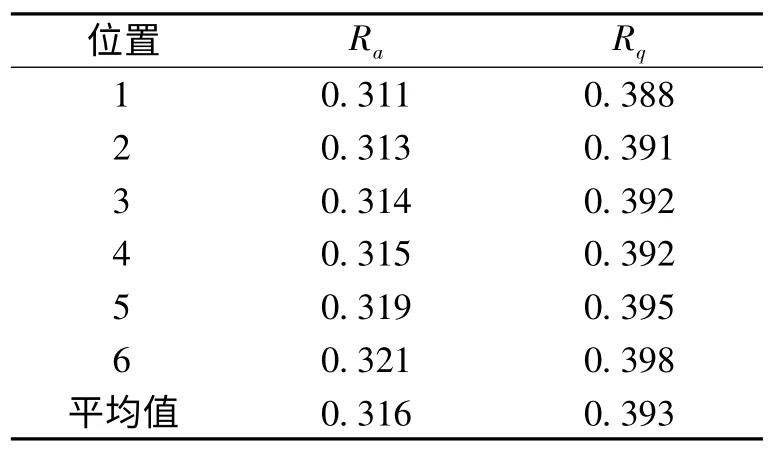
表2 后刀面表面形貌数据采集μm

其中:Ra为轮廓算术平均偏差，Rq为轮廓均方根偏差。

2 基于统计学的工件与车刀后刀面细观尺度接触模型建立及仿真

2．1 车刀后刀面表面形貌的表征

粗糙表面微凸体的高度服从高斯分布:

微凸体的曲率半径为R:

微凸体的概率密度为η:

以上3个公式中:f(x)为微凸体高度分布概率密度函数;R为微凸体的曲率半径;η为微凸体的分布密度;σ为微凸体均方根高度;σ'为均方根斜率;σ″为均方根曲率。

由实验结果可知，轮廓均方根偏差Rq为车刀后刀面表面形貌粗糙度均方根值，且有σ=Rq=0．393 μm，代入公式(1)中可得:

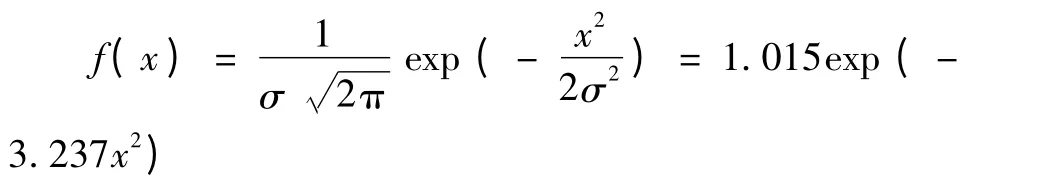
因此车刀后刀面由微凸体高度分布概率密度函数为f(x)，微凸体曲率半径为R，分布密度为η的粗糙表面组成。

2．2 车刀后刀面接触模型的建立

根据经典G-W模型［7］的假设，研究工件和车刀接合面的接触性质即是研究一粗糙面与一刚性平面的接触性质，工件与车刀后刀面接触的细观形貌如图4所示。

图4 工件与车刀后刀面接触的细观形貌示意图

图中d为刚性理想平面与微凸体高度基准平面之间的距离，δ为微凸体的实际变形量，且有:

Hertz弹性接触模型只是对单对接触点的接触建模分析。为了便于计算，研究粗糙表面接触最开始的方法是将两个粗糙表面间的接触假设为一个等效粗糙平面和一个理想刚性光滑平面的接触。

根据Hertz接触模型［8］，单个峰的接触有:

式中:a为Hertz模型接触面积，p为接触载荷，R为微凸体半径，E'为符合弹性模量，即:

式中:E1、E2和υ1、υ2分别代表两接触体材料的弹性模量和泊松比。如表3所示。

表3 车刀和工件的弹性模量和泊松比

因此，高度为x的微凸体发生接触的概率为:

如果接触表面的微凸体有N个，则实际接触的微凸体个数可表达为

其中N=ηAa，Aa为名义接触面积。

由公式(1)、(4)、(5)、(7)、(8)得出实际接触面积和接触载荷为:

式中:A为表面微凸体实际接触面积;

p为表面微凸体实际接触载荷。

2．3 工件与车刀后刀面接触模型的数字仿真运算

2．3．1 后刀面接触模型的量纲一化

为了能够得到实际接触的微凸体个数的变化规律，这里将公式(8)进行量纲一化［9］，令x*=，则有;量纲一距离，微凸体量纲一数量，则有:

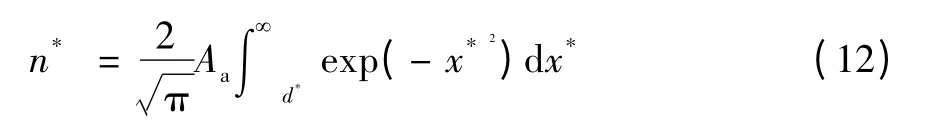
这里有余补误差函数erfc(d*)，定义如下:

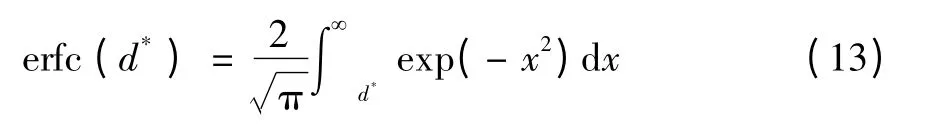
于是，实际接触的微凸体个数n的函数关系式，

2．3．2 工件与车刀后刀面接触模型的仿真运算

通过数学软件Matlab进行仿真分析，进而得到微凸体量纲一数量n*和量纲一间距d*的变化规律，给定d*为［0，3］，如图5所示。

依据仿真结果可知:

(1)随着工件与车刀后刀面高度基准平面之间距离的减少，实际接触的微凸体的个数呈线性增长，且增长的速率越来越快，同时实际接触载荷和接触面积也相应的增加，这与实际情况相符;实际接触的微凸体个数并没有随着名义接触面积的增加而线性增加。

(2)微凸体实际接触变形并非绝对为线性，接触变形逐渐由弹性变形向弹塑性变形转化，这完全符合实际弹塑性接触理论。

3 结论

采用TR200手持式粗糙度仪对硬质合金车刀后刀面的表面形貌参数测量，获取后刀面表面形貌的评定参数，并建立了工件与车刀后刀面间基于统计学的细观接触尺度模型。此数学模型反映了车刀后刀面表面形貌的分布规律及工件和车刀后刀面接合面间的变形机制，为减少硬质合金刀具磨损的研究提供了理论基础，对于研究刀具磨损具有重要意义。

［1］杨雷．钛合金切削摩擦磨损的试验研究［D］．南京:南京航空航天大学，2010．

［2］李友生，邓建新，张辉，等．高速车削钛合金的硬质合金刀具磨损机理研究［J］．摩擦学学报，2008，28(5):444-447．

［3］陆丰玮，李乐洲，朱平国，等．车削TC4钛合金的刀具磨损与切屑形态分析［J］．航天制造技术，2009，6(3):18-21．

［4］刘鹏．超硬刀具高速铣削钛合金的基础研究［D］．南京:南京航空航天大学，2011．

［5］TR200手持式粗糙度仪使用说明书．

［6］吴芝亮．质子交换膜燃料电池接触电阻数学建模与参数分析［D］．天津:天津大学，2008．

［7］GREENWOOD J A，WILLLIAMSON J B P．Contact of Nominally Flat Surfaces［J］．Proceedings of Royal Society，1966，A295:300-319．

［8］JOHNSON K L．Contact Mechanics［M］．Cambridge:Cambridge University Press，1987．

［9］陈士刚，胡亚辉，何志祥．基于统计学规律的机床导轨接合面接触模型研究［J］．润滑与密封，2012，37(12):52-55．