数控机床进给系统精度保持性研究
2015-04-26王义强胡斌峰杨林霖
王义强,胡斌峰,杨林霖
(1.浙江大学宁波理工学院,浙江宁波 315100;2.浙江大学机械与能源工程学院,浙江杭州 315000)
0 前言
随着现代制造技术的飞速发展,数控机床作为最普遍、最重要的现代工作母机[1],自20世纪50年代诞生以来[2],以其强大的柔性制造能力得到了飞速发展与广泛应用。然而,国产数控机床在精度保持性上一直落后于国外高端产品[3-4],这也导致了国产数控机床国内市场占有率普遍偏低。精度保持性不仅体现在机床进给系统的定位精度,更重要的是机床在长时间工作中,持续保持原有定位精度和重复定位精度的能力。目前国家标准一直没有对机床的精度保持性进行严格的定量规定,而实际操作中的各种原因也导致了对机床的精度保持性的评估一直是业内的一项难题。缺乏良好的精度保持性,数控机床的质量就没有保证,其理论研究和生产实践均受到制约[5]。因此,对国产数控机床进给系统的精度保持性进行试验研究,分析其衰减变化模型,可以有效增强数控机床的可靠性。
1 精度保持性理论模型
1.1 精度保持性定义
1.1.1 精度失效事件
精度失效事件通常是指进给系统实际工作精度超出规定的工作精度范围,这里的工作精度主要指系统的单向定位精度、双向定位精度和重复定位精度。对于文中而言主要研究机械部件的磨损、疲劳等有害过程对机械传动系统定位精度产生的影响,因此为了排除伺服系统、部件间隙对测量结果的影响,只对其单向定位精度进行可靠性分析及建模。因此文中精度失效事件指的是进给系统前后两次测量得到的单向定位精度的变化量,超过了预先规定的最大变化值。
1.1.2 精度保持时间(距离)
精度保持时间(距离),指的是相邻两次精度失效事件的间隔时间(距离)。这里的时间是广义的,可以是系统连续工作的时间或累计移动的距离。
1.1.3 精度可靠度和精度失效概率
精度可靠度R(x),指的是进给系统在考察行程x内不发生精度失效故障的概率。精度失效概率F(x),指的是在考察行程x内产品发生精度故障的概率。产品在行程x的单位距离内发生失效的概率称作失效概率密度函数f(x)。
1.2 非齐次泊松过程(NHPP)
在规定的条件与时间内,产品完成规定功能的能力称为可靠性[6]。进给系统精度失效是在多种过程共同作用之下产生的结果[7],例如导轨的振动、丝杠的磨损等,且这些过程通常都是随机的。所以,精度失效事件的发生具有随机性,并且服从一定的概率分布,因而可以参照可靠性统计模型进行数据分析。
文中的可靠性预测模型主要是考察随着行程累积产品故障次数的变化规律。记N(x)(x>0)为产品在(0,x]内的累积故障次数,非齐次泊松过程是指同时满足以下3个条件的计数过程[8]:
(1)N(0)=0,且N(x)是累积行程x的非减函数;
(2){N(x),x>0}具有独立增量,即在行程区间(0,s]与(s,x]内发生的故障次数N(s)与N(x)-N(s)是相对独立的;
(3)在短时间段(x,x+h]内,发生一次故障的概率为:产品在行程区间(x,x+s]内累计故障次数为k的概率为:

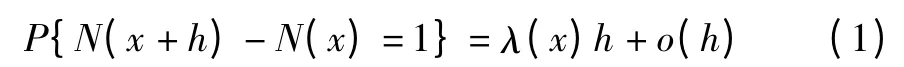
其中:λ(x)为失效率函数,是指单位行程内产品失效的次数;均值函数为,表示(0,x]内产品平均失效次数。
1.3 预测理论模型
AMSAA理论描述的幂律过程是非齐次泊松过程(NHPP)的一种[9-10],其失效率函数和均值函数分别如下:
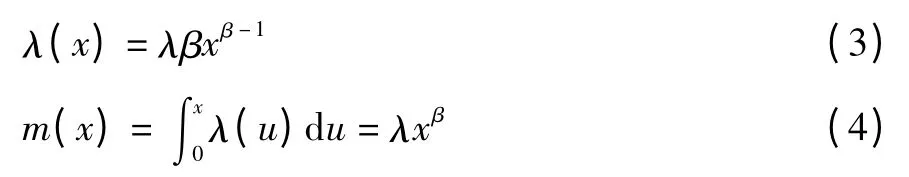
其中:λ>0,β>0。
设数组(x1,x2,…,xn)是计数过程N(x)观测到的n次精度故障对应的累积行程Xi(i=1,2,…,n)的样本值,且x1≤x2≤…≤xn。为了得到(X1,X2,…,Xn)的联合密度函数,需对精度故障发生区间的概率进行分类。若(X1,X2,…,Xn)的联合密度函数为f(x1,x2,…,xn),则在n个小区间(x1,x1+d x1],(x2,x2+d x2],…,(xn,xn+d xn]上各发生一次精度故障的概率为:

令Ai(i=1,2,…,n)表示在区间(xi,xi+d xi]上发生1次精度故障的事件,Bi(i=1,2,…,n)表示在区间(xi,xi+1]上没有发生精度故障的事件。则观测到样本所代表的事件可以表示为Bi,因此根据NHPP过程理论:

对应的对数似然函数:

则可以得到似然函数偏微分方程组:

根据上述方程组,可以得到λ,β最大似然估计值分别是:

则式(14)化简为:

该式是一个典型的非线性方程,运用MATLAB软件可以进行求解。
2 进给系统精度保持性试验
2.1 试验台设计
为了在实验室条件下模拟其精度随工作时间的衰减变化过程,进行加速寿命试验可以在较短时间内使进给系统精度故障暴露出来。本试验方案基于恒定应力加速寿命试验理论,设计了滚动直线导轨副试验系统,通过气缸对进给试验台施加轴向负载。最终搭建的试验台实物图如图1所示。

图1 试验台实物图
2.2 进给系统轴线定位精度测量方法
伺服电机按照编程指令位置,驱动工作台沿着轴线运动到一系列的目标位置Pi,并在各目标位置停留足够的时间以便测量和记录实际位置。参照标准规定,本方案在420 mm的进给轴线上选取5个点作为测量点,在每个点重复测量5次偏差,测量间距分别是:9,98,102,97,103,11。测量方案如图2所示。

图2 精度测量方案
试验过程中,进给系统以往复加载跑合1 000次为一个测量周期,进行一次定位精度的测量,实验总共跑合1 200个测量周期,累积跑合距离504 km。以远离电机的方向为正方向,布置的测量点按照正方向依次为(P1,P2,P3,P4,P5)。试验暂不分析由反向间隙产生的误差,主要研究单向定位精度。
3 数据处理与验证
3.1 数据预处理
本次计算取前1 000次精度测量结果,此时进给系统累计跑合420 km,相对于设计寿命470 km而言,此次的试验周期较长,可以反映出进给系统定位精度随行程的变化规律。根据试验数据的测量结果,以定位精度单向增大5μm为一个精度故障事件,共统计得到47次精度故障事件。分别记录每次精度故障时的累积跑合次数ki(i=1,2,3,…,47)如表1所示。
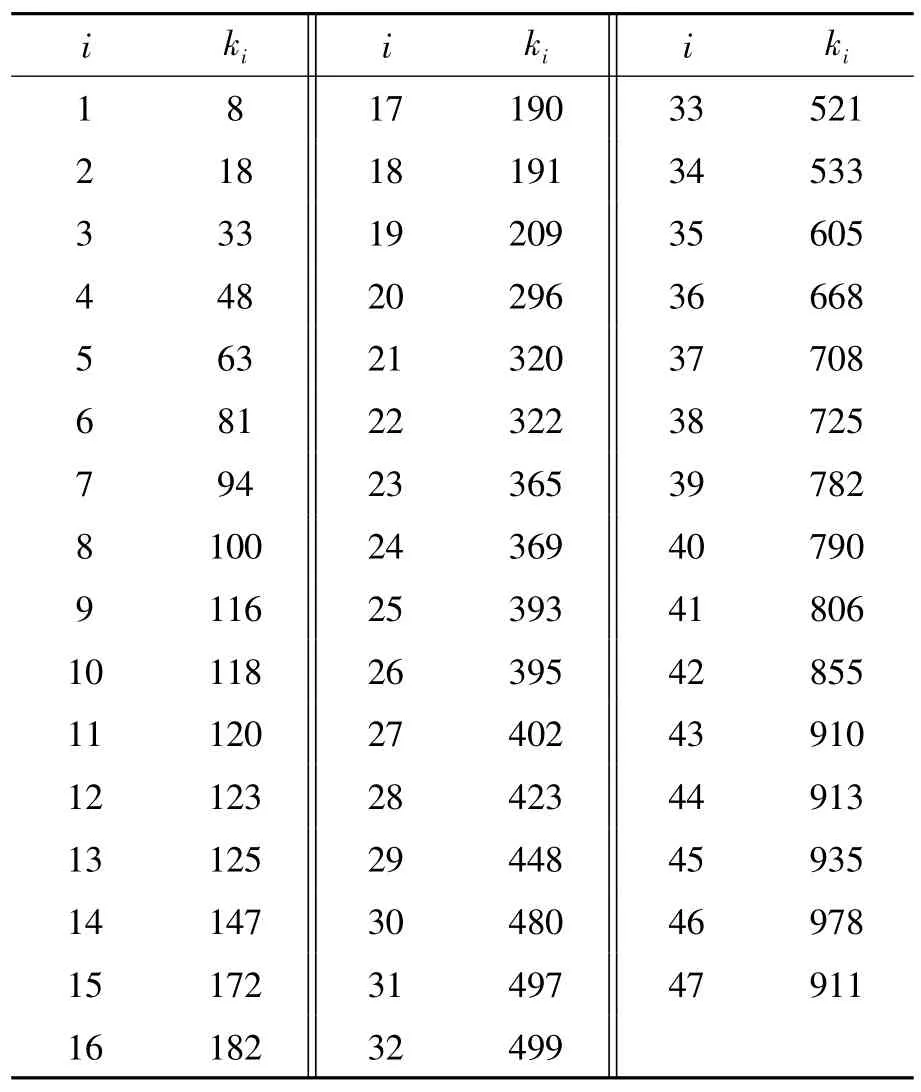
表1 故障累积跑合次数ki记录表
累积行程增量xi(i=1,2,3,…,47)与累积跑合次数ki(i=1,2,3,…,47)关系式:

3.2 参数估计结果
根据公式(12)及(15),以累积跑合次数ki(i=1,2,3,…,47)作为样本值,计算得到:
β=0.655,λ=0.537
则失效率函数:

均值函数:

计算的失效率函数与测量结果拟合情况如图3所示。

图3 失效率拟合曲线
根据分析结果,可以做出以下推断:
(1)在跑合初期,进给系统处于磨合期,随着跑合次数的增加失效率逐渐降低;当跑合次数超过300次后,失效率趋于稳定,进给系统进入稳定期。
(2)进给系统在跑合k次后的定位精度预测公式为:

其中:A0为进给系统初始精度,μm。
4 结论
运用基于AMSAA模型的非齐次泊松过程对定位精度随累积跑合行程的变化规律及其分布函数进行了拟合,根据实验数据对精度保持性模型进行了参数估计,得到失效率函数与均值函数,推导出精度预测公式,并进行了验证。
[1]杨兆军,陈传海,陈菲,等.数控机床可靠性技术的研究进展[J].机械工程学报,2013,49(6):89-98.
[2]ALTINTAS Y.Manufacturing Automation:Metal Cutting Mechanics,Machine Tool Vibrations,and CNC Design[M].Cambridge:Cambridge University Press,2012.
[3]仇健,张凯,李鑫,等.国内外数控机床定位精度对比分析研究[J].组合机床与自动化加工技术,2013(8):1-3.
[4]屠国俊,陶卫军,冯虎田,等.滚动功能部件可靠性研究及其关键技术[J].制造技术与机床,2011(4):17-19.
[5]韦富基,谭顺学.高精度数控机床伺服进给系统精度研究[J].制造业自动化,2012,34(9):69-71.
[6]黄祥瑞.可靠性工程[M].北京:清华大学出版社,1990.
[7]A C普罗尼科夫.数控机床的精度与可靠性[M].李昌琪,遇立基,译.北京机械工业出版社,1987.
[8]王智明,杨建国,王国强,等.多台数控机床最小维修的可靠性评估[J].哈尔滨工业大学学报,2011,43(7):127-130.
[9]杜振华,赵宇,黄敏.基于AMSAA模型的研制试验数据可靠性综合评估[J].北京航空航天大学学报,2003,29(8):745-748.
[10]VAN Dyck J,VERDONCK T.Precision of Power-law NHPPEstimates for Multiple Systems with Known Failure Rate Scaling[J].Reliability Engineering&System Safety,2014,126:143-152.
