基于旋量理论的Stanford机器人的逆运动学分析

王晓磊，李晓丹

(辽宁工业大学机械工程与自动化学院，辽宁锦州 121001)

0 前言

机器人逆运动学也即是求机器人运动学的反解，是指在给定机器人末端执行器的位置和姿态后，求解与该位置和姿态相关各关节的输出变量，它在机器人的运动学、动力学及控制中起着非常重要的作用。它的求解速度和精度直接影响着该机器人运动的快速性和准确性。传统的串联机器人的运动学方程多采用D-H变换矩阵，D-H变换矩阵法相对成熟，但会产生大量的矩阵相乘计算，计算复杂。运用旋量理论可以把复杂的空间机构问题变得十分简单，它已经广泛地应用到机器人领域中［1－5］。

1969年Victor Scheinman设计了Stanford机器人，目前已被广泛地应用于教学和工业生产中。董明晓［6］和赵轲［7］等均在D-H齐次变换矩阵的基础上推导出逆运动问题算法。本文作者对Stanford机器人的逆运动分析采用旋量理论的方法，通过指数积公式建立机器人正运动学数学模型，根据该机器人的结构特点，应用Paden-Kahan子问题求解Stanford机器人的运动学逆解。

1 旋量基础

任何刚体从一个位形到另一位形的运动都可以通过绕空间某直线旋转θ角加上沿该直线的平移距离d合成，此复合运动称为旋量运动。而其无穷小量称为运动旋量，文献［8］详细推导了用运动旋量的矩阵来表示刚体的运动，如公式(1)所示。

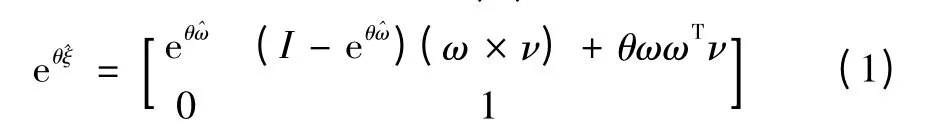
式中:^ξ表示刚体的瞬时速度在SE(3)中的元素，ξ表示关于该轴线的单位旋量坐标。

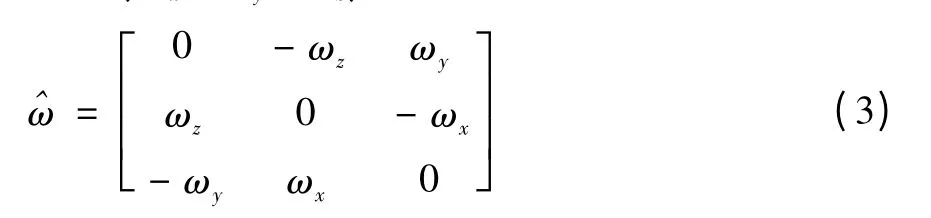
对于多自由度的串联机器人，只需要2个坐标系，即基座坐标系{S}和末端执行器固定的工具坐标系{T}。定义机器人的初始位形为θ=0时位形，用gST(0)来表示。从初始位形时{T}与{S}之间的变换可表示为

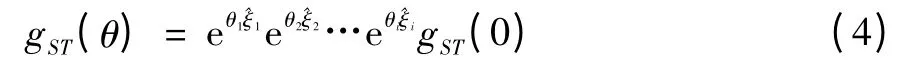
2 Paden-Kahan子问题简介

从式(1)可以看出机器人的各关节变量具有强耦合的特点，若求其运动学逆解必有一定的困难，因此通常利用Paden-Kahan子问题来消除耦合变量，简化求解的工作量。Paden-Kahan子问题主要有2个:

(1)点a沿ξ轴旋转到点b求解满足条件的θ。

(2)一点绕两个有序相关轴ξ1和ξ2的旋转，a、b是空间两点，其求解过程可转化为两个子问题分别求解θ1θ2。θ2为点a绕轴ξ2旋转的角度，接着再绕轴ξ1旋转的角度为θ1，最后点a与点b重合。

上述的2个子问题具体推导过程及求解结果见文献［8］。

3 Stanford机器人的逆解分析

Stanford机器人是一种结构比较特殊的工业机器人，其中前2个关节轴线交于1点，而后三个关节轴线交于一点，结构模型见图1。利用Paden-Kahan子问题求解Stanford机器人的逆解可消除耦合变量，可简化计算量。具体的求解过程如下:

(1)初始位形的选择及指数积正解数学模型建立

取图示位置为参考图形;位置即θ=0时并建立工具坐标系和惯性坐标系。θ为0时惯性坐标系与工具坐标系的变换为

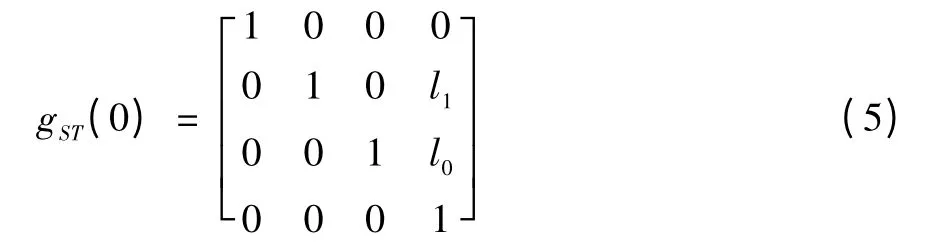
根据式(4)，可得

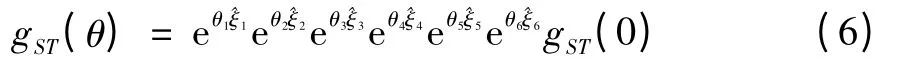
则:

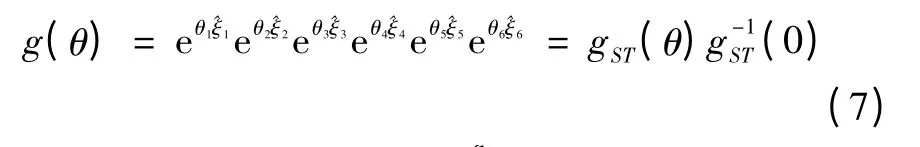
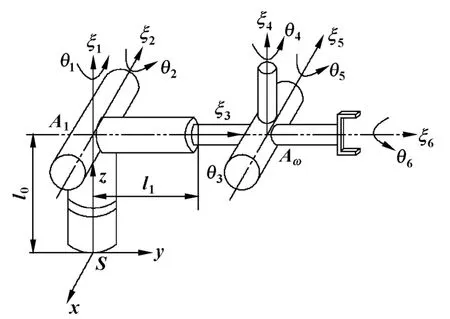
图1 Stanford机器人模型图

(2)求前3个关节变量θ1、θ2、θ3

由于4，5，6轴交于一点Aω，所以位于3轴交点Aω无论后3轴如何旋转其位置保持不变即

将式(7)两边同乘Aω，可得:

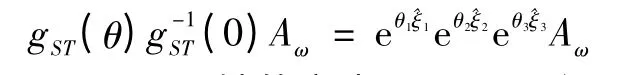
再取1，2轴的交点A1，同理得，

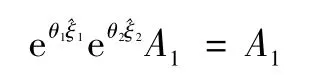
式(8)两边减去A1得:由距离不变原则:

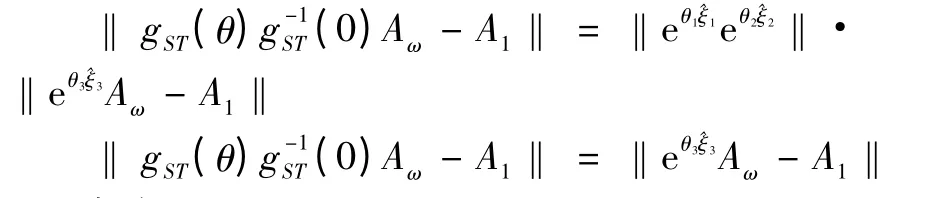
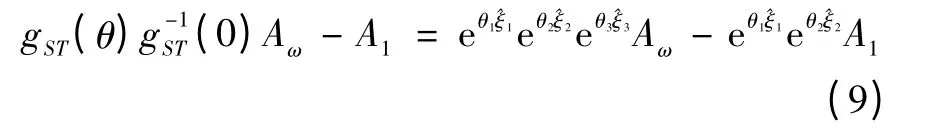
解得θ3。

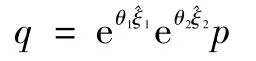
根据Paden-Kahan子问题2可解得θ1、θ2。

(3)求后3个关节变量θ4、θ5、θ6

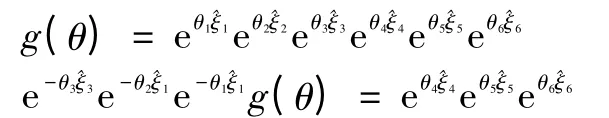
取在6轴，但不在4，5轴一点B，可得

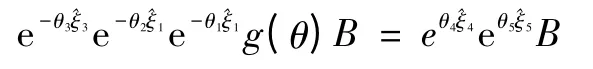
同理根据Paden-Kahan子问题2可解得θ4、θ5。

由已解得θ1～θ5，根据式(7)即可求出θ6。

4 实例验证

Stanford机器人的主要参数

l0=750，l2=300

首先给定角度依据机器人正解方程，求出机器人的末端位姿矩阵，应用上述逆解的求解过程，求出相应的角度。设给定角度

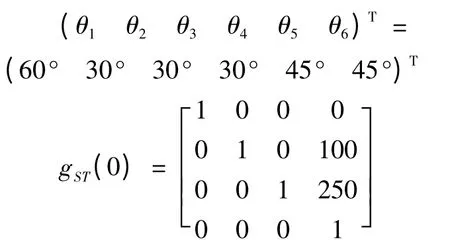
根据正解方程(7)求得末端位姿矩阵:

采用文中给出的逆解方法得出

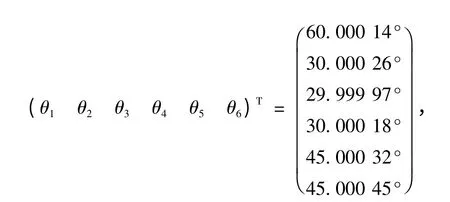
再代入运动学正解位姿矩阵(7)，求得末端姿态得:

比较一下结果可以看出该算法精度较高，接近真实值。

5 结束语

根据Stanford机器人结构特点，采用Paden-Kahan子问题将Stanford机器人运动学逆解问题划分成若干子问题，使其逆解求解更快、更直接，提高了计算效率，有利于计算机对机器人的实时控制;同时通过具体实例验证可知该算法正确，精度较高，为求解Stanford机器人运动学逆解提供了一新途径。

［1］赵杰，刘玉斌，蔡鹤皋．一种运动旋量逆解子问题的求解及其应用［J］．机器人，2005，27(3):163－167．

［2］王小荣，杨晋，刘潇潇，等．仿人机器人基于旋量理论的运动学分析方法［J］．兰州交通大学学报，2009，29(1):72－76．

［3］李君．基于旋量理论的Stanford臂的运动学分析［J］．天津科技大学学报，2010，25(4):72－75．

［4］王科．基于旋量和李群李代数的SCARA工业机器人研究［D］．杭州:浙江大学，2010．

［5］黄勇刚，杜力，黄茂林．基于旋量理论的机器人误差建模方法［J］．哈尔滨工业大学学报，2010，42(3):484－489．

［6］董明晓，张明勤，赵志超．Stanford机器人逆运动问题求解新方法［J］．机床与液压，2001，12(2):52－53．

［7］赵轲．Stanford机器人逆解关节变量新方法［J］．茂名学院学报，2005，15(1):35－36．

［8］理查德摩雷，李泽湘，夏思卡萨思特里，等．机器人操作的数学导论［M］．北京:机械工业出版社，1998．