Delta机器人的误差分析
2015-04-26殷盛江于复生孙中国李腾飞
殷盛江,于复生,孙中国,李腾飞
(1.山东建筑大学机电工程学院,山东济南 250101;2.山东省高校机械工程创新技术重点实验室,山东济南 250101)
0 前言
并联机器人在诸多领域有着广泛的应用,近几年来,许多研究人员在此类机器人的机构设计与运动学分析方面做了大量的工作[1-6]。误差分析对于提升机器人工作性能和品质有着重要意义,针对此类少自由度并联机器人,刘密英等[7]给出了一种机械结构与系统精度的通用计算法,建立了对应的误差模型,进行了误差分析;李宁宁等[8]通过模拟仿真分析了结构误差及相关误差对精度的影响;刘红军等[9]基于四自由度机构的运动学分析,利用摄动法建立了相应的误差模型。这些研究从算法和运动学分析的角度对机构误差进行了分析。文中介绍了Delta机器人的机械造构及造成其位置偏差的误差源,对机械结构和机器视觉部分进行了详细的误差分析。
1 机构设计
该拾取机构为Delta机器人,主要由上固定平台、六根机械臂、下运动平台组成,由伺服电机驱动。Delta机械手下侧可安放诸如传送带等传送装置来输送产品,通过机器视觉识别传送带上的产品,下运动平台上安装有吸盘或机械手,可吸取或抓取传送带上的产品。
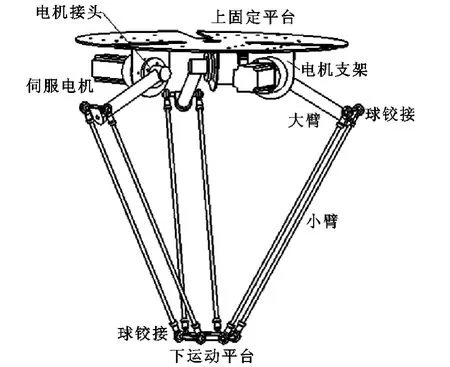
图1 机械结构示意图
上固定平台下方圆周均匀分布3个电机支架彼此成对称分布,电机支架上安装有伺服电机,伺服电机轴端与电机接头相连,电机接头另一端与大臂相连接,大臂下端通过球铰接与小臂相连,小臂另一端与下运动平台通过球铰接相连接,下运动平台与上固定平台相平行,下运动平台在不同高度上平动。当Delta机器人拾取物体时,控制系统控制伺服电机,伺服电机带动大臂转动一个角度,小臂随着上升和偏移,进而带动下运动平台的平动。
2 误差源
Delta机器人通过伺服电机转动的角度θ1,θ2,θ3带动与之相连接的大臂旋转,进而通过大臂带动小臂的旋转,小臂的下方装有与上固定平台平行的下运动平台,通过相关位置正解或反解求出下运动平台的几何中心点P点坐标为(px,py,pz)T,经过相关分析影响这些测量数据的误差源主要有:
(1)伺服电机的旋转角度误差,即编码器的固有误差、计数误差等。这与伺服电机的精度有关,每转发出的脉冲越多,则伺服电机旋转的角度越精确。
(2)机械结构的加工误差及安装误差,在设计机械结构时,基于成本或其他因素考虑,设有一定的余量,连杆理论值应为L,但实际值却为L±Δl,在安装时,理想情况下是上下两个平面是平行的,但实际中却存在着一个角度δθ,造成抓取位置的偏移。这一部分的误差余量,必须加以考虑。
(3)机器视觉识别误差,CCD采集的图像越接近于边缘,越失真。采集图像时,CCD固定在支架上,以俯视的方式采集图像,这种方式失真较大。CCD采集的图像都存在着球差,必须采用相应的补偿措施。
3 模型的建立
3.1 运动学相关方程
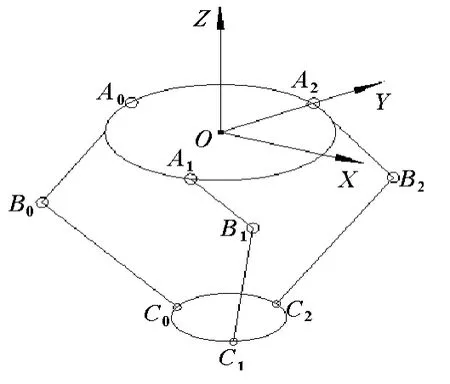
图2 Delta机器人结构简图
以上固定平台的几何中心O为原点,外接圆半径为R,建立O-XYZ坐标系。下运动平台几何中心点P点坐标为(px,py,pz)T,外接圆半径为r,上固定平台上△A0A1A2,下运动平台△C0C1C2都为正三角形。在运动过程中,下运动平台相对于上固定平台实现三维的平动。
根据几何关系,在矢量闭环OPCiBiAiO中,存在以下矢量关系:
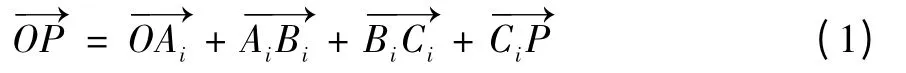
3.2 机械部分误差分析
机械部分影响其精度的主要因素有:并联机构的伺服电机转动角度θ1,θ2,θ3。6根连杆长度l11,l12,l21,l22,l31,l32。
设运动学方程为:
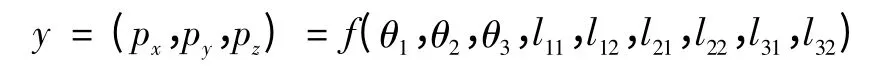
存在以下公式:
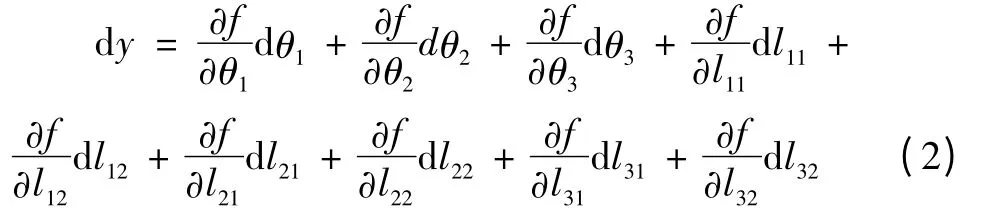
可近似得到下运动平台的几何中心点P点坐标的系统误差:
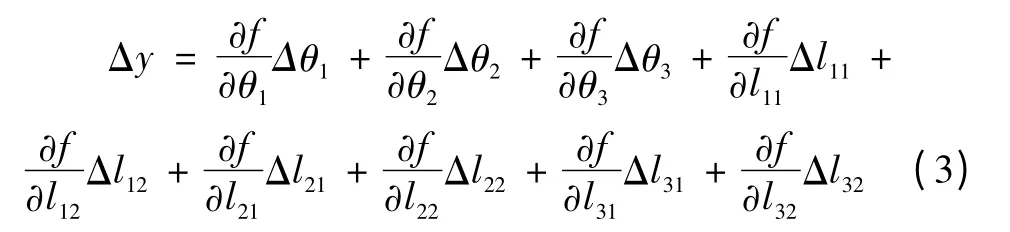
那么点P的实际坐标为:y=y0-Δy
式中:y0为该点的测得值;Δy为该点的测量误差。
如果在理想的不存在任何误差的情况下,那么每次的测量值应为确定值,记录的曲线为一直线;如果有随机误差存在,测量值在算术平均值两侧波动;若存在的系统误差远远大于随机误差,那么数据的变化趋势取决于系统误差的变化,可以根据以下几种方法,来发现和辨别系统误差。
(1)将所测得数据求出算术平均值,将数据对应的偏差,按测量顺序依次排列,如果偏差的变化是有规律的,那么数据中一定含有按照周期性变化的系统误差。
(2)测量值呈现规律性变化,如测量值逐渐增大或减小,那么存在着线性系统误差。如果沿水平方向,测量值按复杂规律变化,间隔一段数据减小或增大,一定存在复杂系统误差。
(3)用正态概率纸判断。正态概率纸横坐标是等距离的刻度,纵坐标是正态分布的刻度。数据的值作为横坐标,纵坐标为出现的频数。如果各点均匀分布,那么只有随机误差,不均匀分布的话,一定存在系统误差。
对点P的坐标进行多次测量时,并不是完全就是在一个点上,说明Delta机器人存在着随机误差,随机误差是用表征其值分散程度的标准差来评定的。随机误差可以有很多种,如连杆之间的摩擦、间隙、环境造成的影响等。
函数的一般形式为:y=f(x1,x2,x3,…,xn)
对连杆摩擦x1、连杆间隙x2、环境影响x3进行N次测量,其相应的随机误差为:
对x1:δx11,δx12,…,δx1N
对x2:δx21,δx22,…,δx2N
对x3:δx31,δx32,…,δx3N
可得点P的坐标的随机误差为:
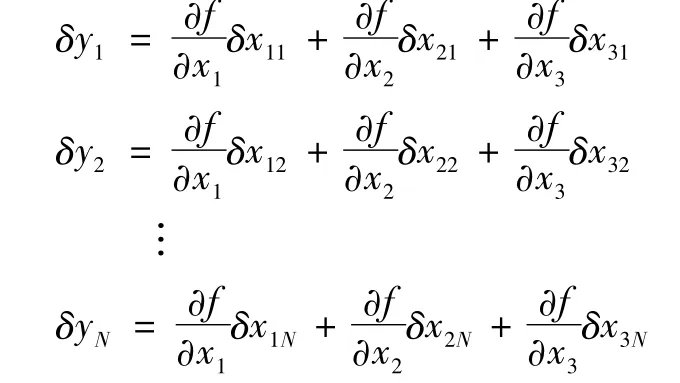
将上式平方相加得:
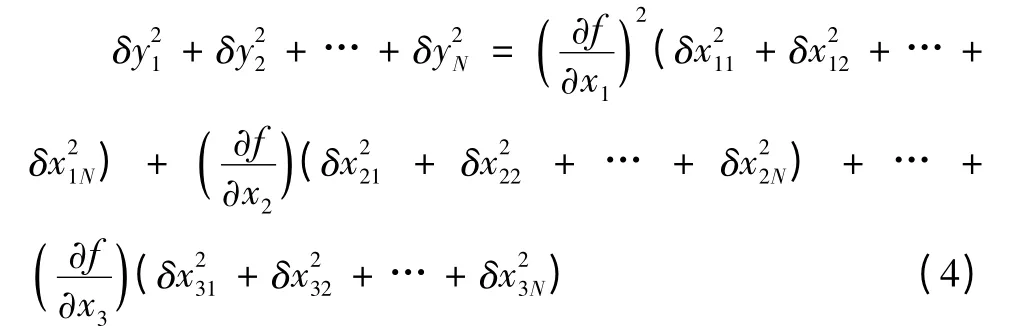
可得方差为:
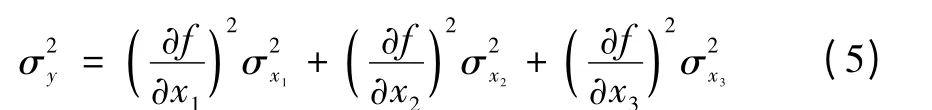
平方差为:
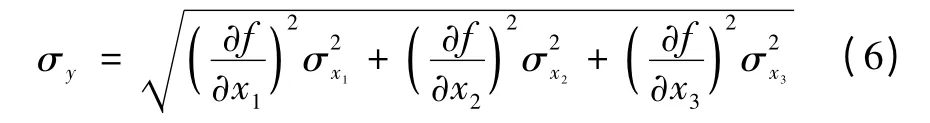
当测量过程中存在各种不同性质的误差时,需要将其综合考虑,求得最后测量结果的总误差,常用极限误差或标准差来表示。
在Delta机器人中,已定的系统误差为l11,l12,l21,l22,l31,l32,未定的系统误差θ1,θ2,θ3,随机误差x1,x2,x3,那么它们的误差值或误差极限分别为:
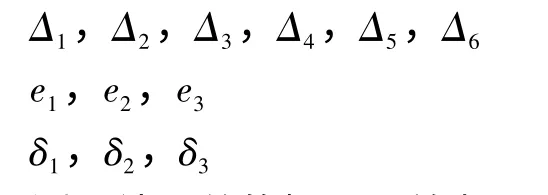
测量结果总的极限误差为:
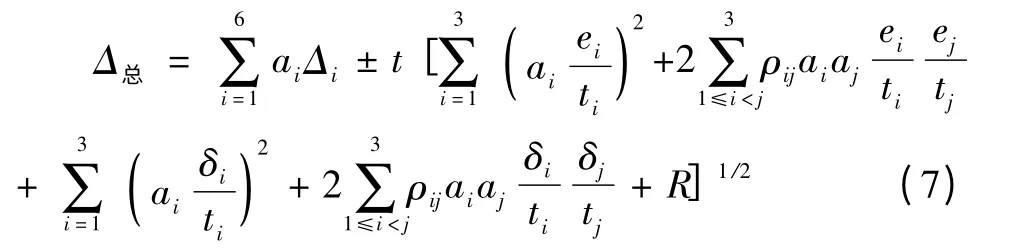
式中:R为各个误差间协方差之和;
t为各单项极限误差的置信系数;
ai为各个误差传递系数;
ρij为误差间相关系数。

表1 像素转化的实际距离
3.3 机器视觉部分误差
机器视觉在日常生活中被广泛应用于测绘、测量和控制。CCD采集的图像,一般带有球差、慧差、像散和畸变等像差。对图像造成失真影响最大的为球差。球差是由于电磁透镜中心区域和边缘区域对电子会聚能力不同而造成的。下面就球差对Delta机器人抓取位置的误差进行分析。
不同高度的平行入射光经过透镜折射后,相交于不同的位置。在焦点F1附近做两个截面L1,L2。可计算得到不同的高度入射光对应焦点的位置:

式中:D为两个截面L1,L2之间的距离,当入射高度为Hn时,球差为δL=Dn2-Dn1。
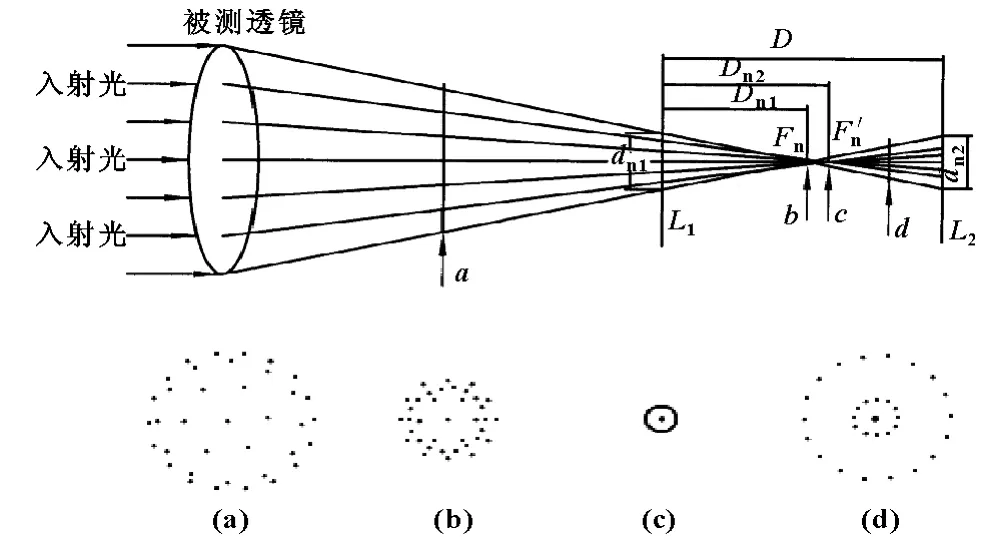
图3 CCD误差原理图
由上式可知,测量误差取决于两个截面L1,L2之间的距离D和截面与焦点之间的距离dn1,dn2。
根据标准误差传递原理,球差测量标准误差可表示为:
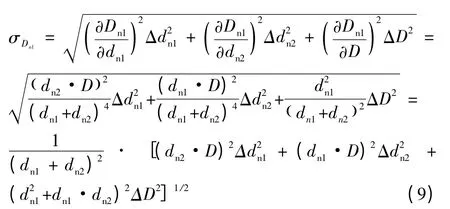
式中:Δdn1,Δdn2,ΔD分别为dn1、dn2和D的测量误差。
CCD采集的图像,一般带有球差、慧差、像散和畸变等像差。随着CCD和计算机技术的发展,光学图像处理数字化已成为必然的趋势。ZEMAX是一个综合性的光学设计仿真软件,它将设计概念、优化、分析、公差以及报表整合在一起。对于分析CCD造成的球差,慧差等像差非常便捷,如图4所示。

图4 ZEMAX分析界面
文中采用方格法进行机器视觉球差的误差处理,进行CCD的标定,具体分析球差造成的影响。
相关参数为:
摄像头像素:1280像素×1024像素
方格纸小方格:5 mm×5 mm
摄像头中心坐标:640像素×513像素
测得数值如表2所示。

表2 每50 mm实际距离像素变化
摄像头1 024像素时,转化为距离理论上应为387.878 mm,而实际测得距离却为410 mm,相差为22.12 mm,即为CCD球差造成的影响。
以方格纸的实际距离为X轴,以像素转化的距离为Y轴,如果不存在球差,那么连线应为45°的直线,实验测得数据如表1所示。
如图5所示,可以看出随着实际距离的增大,球差越来越大,对于下运动平台的抓取位置影响也越大。
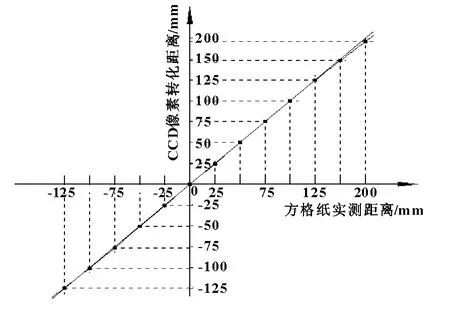
图5 像素距离与实际距离偏差
4 结论
Delta机器人拾取物体位置时,造成误差出现的原因千差万别,它的存在对于机构的定位影响很大。文中在描述Delta机器人的结构的基础上,系统地介绍了造成Delta机器人位置偏差的误差源,通过分离变量的方法,对机械结构和机器视觉部分进行了误差的单独分析与组合分析,给出了详细的误差分析公式,为Delta机器人的误差补偿提供了理论依据。
[1]HUANG T,WHITEHOUSE D J,WANG J S.The Local Dexterity Optimal Architecture and Design Criteria of Parallel Machine Tools[J].Annals of the CIRP,1998,47(1):347-351.
[2]SCHNECKE H J,BECKENBAUER R.Development of Hexapod Based Machine Tool[J].Annals of the CIRP,1998,47(1):337-340.
[3]胡明,原所先,蔡光起.三杆并联平动机器人机构动力学[J].东北大学学报,2003,24(11):1075-1077.
[4]宁凤艳,贠超.四自由度串并联机器人的位姿误差分析[J].机床与液压,2010,38(15):35-37.
[5]张广芸,车仁炜,陆念力.3-DOF平面并联机器人的动力学研究[J].机械制造,2010,48(554):9-11.
[6]张宏涛,陈安军,张权.三自由度并联机器人的运动学分析[J].机械科学与技术,2009,28(4):492-495.
[7]刘密英,黄家贤,叶琪根.机械结构与系统精度通用计算法及其应用—机器人机构误差分析与计算[J].机器人,1992,14(4):18-24.
[8]李宁宁,赵铁石.并联式四自由度定位平台误差分析[J].机器人,2008,30(3):223-230.
[9]刘红军,龚民,赵明扬.一种四自由度并联机构的误差分析及其标定补偿[J].机器人,2005,27(1):6-9.
