四连杆仿生膝关节机构优化设计

张莉洁，卢文涛，曹学民

(洛阳理工学院，河南洛阳471023)

0 前言

在康复医学和双足机器人领域，人工膝关节是重要的功能部件。它可以帮助人体实现站立的支撑和行走时的灵活自然步态。自然人腿膝关节的转动中心会随屈伸动作而移动，即转动运动中心是变化的，如图1 其瞬时转动中心的轨迹为J 型曲线。研发仿生性能良好的人工关节技术是康复工程学及仿生行走机器人学的重要课题。为更好地模拟人腿膝关节功能，采用四连杆仿生膝关节，利用其可变瞬时转动中心的运动学特性，实现膝关节的转动多轴性，其良好的仿生特性得到了市场及大量学者的广泛关注和研究［1－4］。四连杆膝关节机构设计的好坏将决定其仿生性能，已得到国内学者的广泛关注。

图1 膝关节瞬心轨迹图

王斌锐等［3］在设计时同时考虑大腿和小腿的运动，采用旋转矩阵和坐标变换法来表达踝关节轨迹，同时使膝关节和踝关节轨迹与目标轨迹重合。考虑到膝关节的作用只是保证大小腿的相对运动规律，因此设计时无需考虑大腿运动，该方法不必要地将优化问题复杂化，使计算过于繁复。文献［5－6］以转动瞬心的J 型曲线为目标轨迹，使所设计的四连杆机构的瞬心与J 型曲线重合，但考虑到若回转半径长度和位置不同，踝关节中心点轨迹也会不同，因此该方法无法同时保证踝关节轨迹能准确再现人腿实际轨迹，自然步态仍无法实现，该设计方法不够成熟。现有文献中少有对优化后四连杆膝关节瞬心位置的图解说明，其优化结果的仿生性能仍有待进一步论证。

四连杆仿生膝关节机构设计是机构综合问题，即在大腿固定不动的情况下，要求小腿实现相对摆动运动关系，即保证踝关节中心点的轨迹与人腿相应关节中心轨迹重合，属于轨迹生成问题。本文作者根据多轴膝关节的结构特点，考虑小腿摆角范围，摆动期灵活性的要求，以获得实际人腿踝关节的运动轨迹为优化目标，采用多变量优化设计方法对四连杆多轴膝关节机构进行优化设计，使其能获得自然人腿步态，并通过运动仿真得到膝关节瞬心位置，分析验证其运动仿生性能。

1 四连杆膝关节数学模型

1.1 踝关节理想运动轨迹生成

实验人小腿长330 mm，踝关节中心点距离脚后跟40 mm，步态周期0.45 ～0.6 s，将大腿看作机架，通过人小腿摆动试验得到踝关节的真实运动轨迹，如图2 所示。选定目标点，使其准确再现运动轨迹。

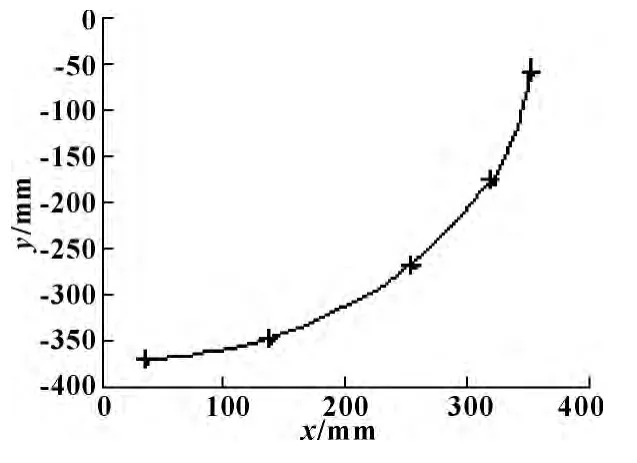
图2 踝关节真实运动轨迹实验数据

1.2 数学建模

为使连杆摆动范围足够大，考虑设计为曲柄摇杆机构，如图3 所示，以铰链点A 为坐标原点建立直角坐标系，其中机架AD为固定不动的大腿，其与x轴的夹角为φ0;杆BM 固连在连杆BC 上，作为仿生机构的小腿，点M 即为踝关节中心点。BM 与BC 的夹角固定为λ;AB 为摇杆，CD 为曲柄，当AB 摆动至位置i 时，与机架AD 的夹角为φi。

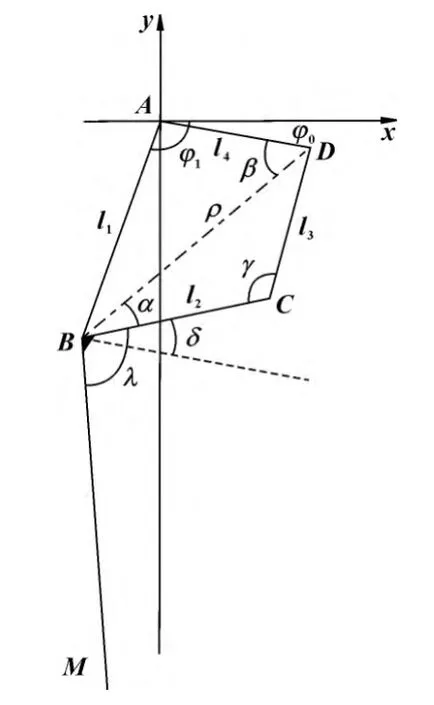
图3 四连杆膝关节机构模型

对应连杆上点M 坐标可用下列函数表达为:

其中，λ 由BC 转向BM，为负值，ρ 为BD，用自变量表达为:

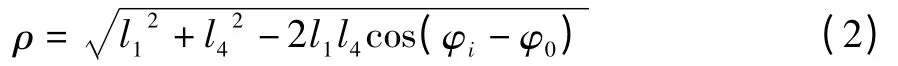
其中，β=∠ADB;γ=∠BCD;α = ∠DBC;δ 为BC与AD 间的夹角，其值可按如下计算:

由以上知，点M 坐标是杆长l1，l2，l3，l4，l5，角度φ0，λ，φi的函数。φi为摇杆摆动至图3 目标点处对应的摇杆摆角，由此可确定设计变量为:

x= ［x1x2x3x4x5x6x7x8x9x10… xm］T= ［l1l2l3l4l5φ0λ φi］T，其中x8…x7+m为对应m 个目标点相应摇杆的转角φi。由上可知，设计变量除了曲柄摇杆的结构尺寸参数外，还有对应各个目标点位置的摆角值，若取5 个目标点，则设计变量为12 个，若选取目标点m 个，则设计变量为7 +m 个。

1.3 目标函数的确定

优化目标为连杆BC 上点M 的实际轨迹与目标轨迹重合。因此，以点M 实际轨迹上若干个点的坐标与理想轨迹上目标点的误差均方根最小作为优化目标。在实际优化计算中，采用加权方法使目标函数能够收敛，其函数表达式为:

式中:Sxi，Syi是踝关节理想轨迹的第i 个目标点坐标;Mxi，Myi是连杆BC 上点M 实际轨迹上第i 个点的坐标，ωi为保证收敛的加权值。

1.4 确定约束条件

约束条件为不等式约束，表达式为gi(x)≤0。要成为曲柄摇杆机构，且使CD 杆l3为曲柄，应满足如下杆长条件:

膝关节应保证摆动期灵活性，要求最小传动角∠ABC≥30°，最小传动角出现在曲柄CD 与机架共线的位置，即满足以下非线性不等式:

根据膝关节尺寸比例限定设计变量边界条件:

70≤l1≤110;60≤l2≤90;35≤l3≤60;40≤l4≤70;260≤l5≤290;－15≤φ0≤15;－120≤λ≤－90;－90≤φi≤－70，等。

2 优化结果仿真分析［5-6］

2.1 初值的选定

优化过程若在大范围内盲目搜索较为不易，且只能求出局部最优解，因此为节省优化时间，保证正确的搜索方向，应先找出较为合理的初值。

根据膝关节尺寸比例，初定机架l4长度50 mm。考虑到支撑期的稳定性，初设AD 夹角φ0=0°。采用图解法取定初值，x = ［78 63 40 50 284 0－119－85－60－43－35－31］。

2.2 优化结果

该问题属于非线性约束优化问题，设计采用二次规划算法。二次规划法利用拟牛顿法 (变尺度法)来近似构造海赛矩阵，确定搜索方向，建立二次规划子问题进行迭代求解，因此又称约束变尺度法。

Hessian 矩阵采用拟牛顿法进行迭代，变尺度矩阵的迭代公式采用稳定的BFGS (Broyden-Fletcher-Gold farbshanno)算法。

本次设计借助MATLAB 软件优化函数fmincon 进行，由于该优化问题含有非线性约束，且希望计算更为准确，采用medium-scale 的SQP 算法。优化语句为:

［x，fval］ = fmincon (@ mygoal，x0，A，b，［］，［］，lb，ub，nonlcon，options);其中，A，b 为公式(8)的矩阵表达式，nonlcon 为公式(9)非线性函数。@mygoal 为目标函数，即为该优化问题的数学模型，采用式(1) ～ (7)表达。

若初值选择不同可得不同的优化结果，因此优化算法只能求出局部最优解，选取较好的一组优化结果如表1，实际轨迹与目标轨迹误差为5.65 mm。

表1 四连杆机构结构参数优化结果

为验证优化后的四连杆膝关节仿生特性的好坏，应给出瞬心轨迹。对四连杆膝关节进行运动分析得其瞬心坐标表达式为:

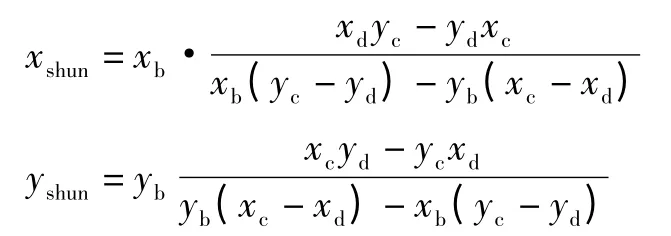
图4 为优化结果与目标轨迹的比较，左上方十字轨迹为瞬心轨迹，其曲线形状为J 型，进一步分析运动特性。

图4 优化结果实际轨迹与目标轨迹比较

图5 为运动仿真，显示出摇杆以均匀摆角摆动时四杆机构运动的动态过程，仍画出瞬心轨迹。由图分析得，在运动初始位置即支撑期，其瞬心位置较为靠上，即膝关节伸展时，转动中心大大高于连杆机械轴的位置。而在膝关节屈曲时，即之后的摆动过程中，瞬心随膝屈曲急速下降，回到通常膝轴的位置。这样使得支撑初期小腿长度变化，可减少稳定膝关节所需的髋关节伸展肌力，确保了大腿假肢的支撑期稳定性;而在摆动中期膝轴高度下降至正常位置，保证正常自然的运动姿态，实现完美步态。

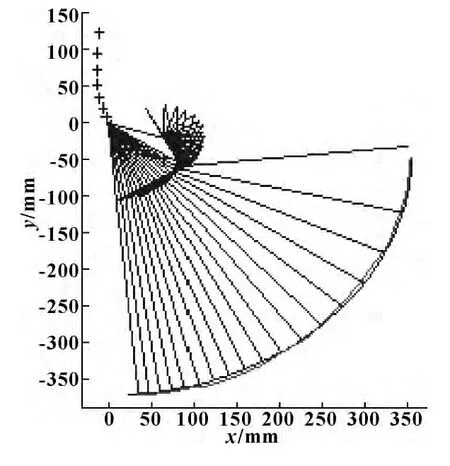
图5 四杆机构运动的动态过程

以上分析充分验证了所设计的四连杆膝关节机构具有良好的仿生性能，该仿生关节能获得人腿自然步态。

图6 为优化后四连杆的初始位置，即支撑期位置，图中看到瞬心位置位于髋踝线TA 线前方［7－8］，则地面支撑反力将对瞬心产生驱动小腿摆动的力矩，因此支撑期稳定性稍差，在此可采用智能磁流变阻尼器实现自承重自锁式结构，即在连杆和机架间合适位置处安装磁流变阻尼器［9］，在支撑期，调整阻尼力为最大，从而实现自锁承重。在摆动期，可调阻力的磁流变阻尼器与电机共同工作，使其在运动中获得良好的减振性能。

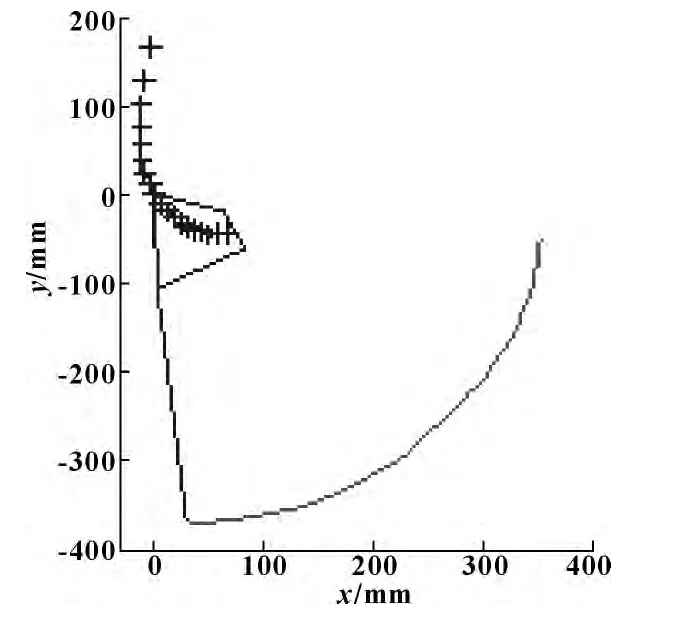
图6 优化四连杆初始位置及瞬心位置比较

3 结论

采用二次规划优化设计方法对四连杆仿生膝关节进行优化，并通过运动仿真对优化四连杆机构进行仿真，得到以下结轮:

(1)所设计四连杆机构在小腿摆动过程中，实际轨迹与目标轨迹吻合度良好，其速度瞬心呈J 型曲线，符合人腿自然步态，充分验证了四连杆膝关节良好的仿生特性。

(2)所设计四连杆机构在支撑期时速度瞬心位置较为靠前，有利于摆动期灵活性，适合运动灵活性的使用要求，为保证支撑期的稳定性推荐采用加装智能磁流变阻尼器的自锁承重式结构。

(3)应进一步对仿生膝关节驱动小腿摆动过程进行速度、加速度分析，考虑阻尼器的安装，并进一步验证其动力学性能。

［1］刘娜，刁兴建．假肢膝关节概述［J］．中国矫形外科杂志，2006，3(2):225－226．

［2］杨义勇，王人成，王延利，等．新型仿生膝关节的机构设计与仿真［J］．中国机械工程，2008，19(1):72－79．

［3］王斌锐，许宏，金英连，等．双足机器人四连杆仿生膝关节的研究［J］．机械设计，2006，7，23(7):13－15．

［4］吴成东，金基准，闻时光，等．基于混合驱动仿生膝关节机构设计［J］．沈阳建筑大学学报，2012，7，28(4):759－764．

［5］吴希瑶，翟少剑，郝倩．假肢膝关节四杆机构的优化与仿真［J］．机械设计，2011，28(9):42－45．

［6］李燕．基于Pro、Mechanism 的仿生膝关节优化设计与运动仿真研究［J］．机床与液压，2009，37(6):183－185．

［7］张培育，金德闻．多轴膝关节假肢稳定性的分析［J］．中国康复医学杂志，1998，13(1):18－20．

［8］RADELIFFE CW，DEG M S，PROFESSOR M E．Biomechanics of Knee Stability Control with Four-bar Prosthetic Knee ［C］．ISPO Australia Annual Meeting Melboume，Australia，2003:33－36．

［9］CHEN J Z，LIAO W H．Design，Testing and Control of a Magnetorheological Actuator for Assistive Knee Craces［J］．Smart Materials and Structures，2010，19(3):29－35．