桁架式Spar平台与系泊/立管系统的全时域非线性耦合动态分析
2015-04-25杨敏冬宁德志时忠民1中国能源建设集团广东省电力设计研究院有限公司广州10662中国海洋大学海洋工程系山东岛266100大连理工大学岸和近海工程国家重点实验室辽宁连11602中国海洋石油研究中心北京100027
杨敏冬,滕 斌,宁德志,时忠民(1中国能源建设集团广东省电力设计研究院有限公司,广州 5 1066;2中国海洋大学海洋工程系,山东 青 岛266100;大连理工大学 海 岸和近海工程国家重点实验室,辽宁 大 连11602;中国海洋石油研究中心,北京100027)
桁架式Spar平台与系泊/立管系统的全时域非线性耦合动态分析
杨敏冬1,2,滕 斌3,宁德志3,时忠民4
(1中国能源建设集团广东省电力设计研究院有限公司,广州 5 10663;2中国海洋大学海洋工程系,山东 青 岛266100;3大连理工大学 海 岸和近海工程国家重点实验室,辽宁 大 连116024;4中国海洋石油研究中心,北京100027)
开发了对浮式平台系统进行耦合动态分析的全时域程序。采用二阶时域方法计算水动力荷载,在此方法中,对物面边界条件和自由水面边界条件进行泰勒级数展开,利用Stokes摄动展开分别建立相应的一阶、二阶边值问题,而且此边值问题的计算域不随时间变化。采用高阶边界元方法计算每一时刻流场中的速度势,利用四阶预报校正法对二阶自由水面边界条件进行数值积分。在自由表面加入一个人工阻尼层来避免波浪的反射。对于系泊缆索/立管/张力腿的动力分析,在一个总体坐标系中对控制方程进行描述,采用基于细长杆理论的有限元方法进行求解。在耦合动态分析中,采用Newmark方法对平台和系泊缆索/立管/张力腿的运动方程同时进行求解。利用开发的耦合分析程序对一个桁架式Spar平台的运动响应进行了数值模拟,给出了平台的位移和系泊缆索/立管上端点的张力,并得到了一些重要结论。
全时域;桁架式Spar平台;系泊缆索;有限元;耦合动态分析
0 引 言
Spar,TLP和FPSO等浮式平台在深水油气开采中得到了广泛的应用。随着水深的增加,系泊缆索和立管的质量及其阻尼对平台运动的影响越来越大。因此,考虑平台和系泊/立管系统之间的动力相互作用变得非常重要。Ma[1],Lee和Flory[2],Lee和Devlin[3],Kim等[4-5]研究发现,在深水环境中,传统的解耦或准静态分析可能会得到不可靠的结果。
在这种情况下,为了全面考虑浮式平台和系泊缆索、立管之间的各种相互作用,必须进行耦合动态分析。在目前的海洋工程工业界,人们越来越推荐在深水应用中采用耦合动态分析工具。在这种趋势下,Ran[6]和Garrett[7]开发了完全耦合动态分析时域程序,Kim等[8]利用此程序对一个6 000英尺水深中的转塔式系泊游轮FPSO进行了整体运动响应模拟,并将数值模拟结果与美国德克萨斯A&M大学海洋工程研究中心(OTRC)的1:60模型试验结果进行了对比,结果吻合良好。Tahar和Kim[9]开发了一套理论和数值求解工具对采用聚酯系泊缆的深水浮式平台进行耦合动态分析。在他们的论文中,建立了具有大变形和非线性应力应变关系的聚酯缆索计算模型。Low和Langley[10]提出了一种混合时域/频域方法对船舶/系泊缆索/立管进行耦合分析,在相对浅的水深中,该方法可以得到与完全耦合时域分析一致的结果。Chen等[11]在计算中仅考虑莫里森波浪荷载,并将小型张力腿平台的数值结果与测试结果进行了对比。Zhang等[12]对多柱桁架式Spar平台的耦合影响进行了研究。分别采用了准静态耦合、半耦合和全耦合三种方法来模拟Spar平台系统,并将频域和时域的分析结果与试验数据进行了对比。
然而,前期对系泊结构与其系泊系统之间耦合效应的研究一般采用类似的方法(de Kat和Dercksen[13];Ran和Kim[14];Ormberg和Larsen[15];Ran等[16];Ormberg等[17];Tahar等[18];Yang和Kim[19])。首先在频域内计算水动力系数,然后基于平方传递函数和入射波浪谱,利用快速傅里叶变换(FFT)和随机相位假定在时域内计算作用在结构上的波浪力,此方面的研究还包括采用莫里森方程计算拖曳力。对于系泊系统的动力分析,采用有限元法(FEM)或集中质量法在时域内进行求解。通过匹配导缆孔处的力和位移,将系泊结构与其系泊系统进行耦合。
在本文的研究中,建立了一种全时域分析模型对浮式平台系统进行耦合动态分析[20]。这种新的耦合分析方法不需要过多的人工参与,并且可以非常方便地处理各种非线性的影响。采用基于高阶边界元的二阶时域分析方法计算水动力荷载[21],该方法利用泰勒级数展开和Stokes摄动展开分别建立相应的一阶、二阶边值问题,通过时间积分方法更新波面和自由表面上的速度势。基于细长杆理论[22],在一个总体坐标系中描述系泊缆索/立管的控制方程,采用有限元方法对系泊缆索/立管进行动力分析,该方法不需要坐标变换,比传统的有限元方法更加有效[23]。通过在系泊点施加充分的边界条件,将平台动力程序与系泊动力程序在时域内进行耦合。在每个时间步,利用Newmark法和N-R迭代法对浮式平台运动方程和系泊缆索/立管动力方程同时进行求解。
利用本文的全时域耦合模型对一个系泊缆索/立管约束的桁架式Spar平台进行了计算分析。采用了两种不同的数值方法模拟规则波作用下Spar平台的运动响应和导缆孔处系泊缆索/立管的张力:准静态耦合方法(COUPLE_QS)和动态耦合方法(COUPLE_DY)。两种方法采用相同的方式计算作用在结构上的波浪荷载,不同的是COUPLE_DY在计算中考虑了系泊缆索/立管的动态力的影响,而COUPLE_QS忽略了这种影响。为了进行对比验证,结果中同时给出了采用QTF方法计算得到的Spar平台的运动响应。通过不同数值模拟结果的比较,揭示了桁架式Spar平台与其系泊/立管系统之间的动力耦合效应。
1 二阶时域波浪与物体相互作用分析方法
计算中定义了两套右手直角坐标系(见图1),一个为原点在静水面上的空间固定坐标系Oxyz,x和y为水平坐标,z为向上的垂直坐标。另一个为固定在物体上的坐标系O′x′y′z′。当物体处于平衡位置时,两个坐标系重合。
基于理想流体假定,流体的运动可以通过一个速度势函数φ来表示,该速度势在流体域Ω内满足拉普拉斯方程和相应的边界条件。利用泰勒级数展开,可以将瞬时物体表面和自由水面上的非线性边界条件变换到平均物面和静水面上满足。引入Stokes摄动展开方法,将速度势、波面升高和物体运动按照小参数ε展开为如下的级数形式:



图1 坐标系定义图Fig.1 Definition sketch of coordinate systems
其中:下标w和s分别表示入射波和散射波分量;上标(1)和(2)分别表示一阶和二阶波分量。将Stokes摄动展开代入拉普拉斯方程和在平均物面及静水面上展开的边界条件,可以分别建立一阶和二阶边值问题。
对于k阶波浪辐射问题(k依次为1和2),散射势在流体域Ω内满足拉普拉斯方程

在海底、平均物体表面和静水面上满足的边界条件分别为:

式中:fk、fk′和fk″分别定义如下:

其中:n为指出流体的物面单位法向量,H定义为:

为了避免散射波在计算域外边界上的反射,引入一个人工阻尼层来吸收波浪。在自由表面的外部区域上,在自由表面边界条件中加入一个阻尼项:

其中的阻尼系数表达为

式中:α、β为系数,本文均取为1.0;ω为入射波频率;λ为入射波波长;r0为阻尼层内径的大小。
选取Rankine源和它关于海底的镜像作为格林函数,利用格林第二定理,可以得到关于计算域边界上散射势的边界积分方程

然后采用高阶边界元方法可以建立一套线性代数方程组:

其中:[A]和{B}均为系数矩阵。
在每一个时间步求得散射势φs(k)以后,作用在物体上的波浪力可以通过平均物面上的压力积分求得。按照小参数ε进行分离,总波浪力可以根据不同的阶次划分为若干项:

零阶项为浮力

一阶项可进一步划分为:

其中:FD(1)为动态压强在物面上积分得到的动态力;FS(1)为物体运动引起的恢复力;AWP为平均水面面积;(xf,yf)为平均水面中心坐标;X0=(x0,y0,z0)为转动中心坐标;k为z方向单位向量。
二阶项可以表达为:

采用相同的处理方法,三个波浪力矩分量可以划分为
学校“现代杯”口腔技能大赛奖励办法:(1)每个竞赛项目各设一等奖1名,二等奖3名,三等奖5名,优秀奖10名;由学校和现代公司联合颁发荣誉证书并给予一定的奖金。(2)获奖学生若选择到现代或洋紫荆公司实习,将提前两个月转正,并享受正式工的工资待遇。(3)获一、二、三等奖的选手,可获得由学校推荐到优质企业顶岗实习、就业的机会,并直接获得全国“日进杯”学校参训选手集训机会。
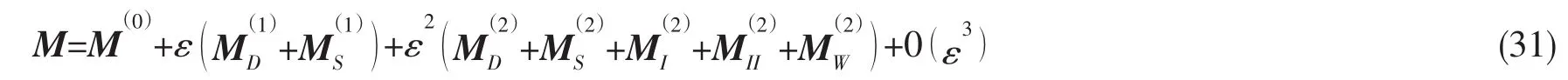
零阶项为浮力矩

式中:(xb,yb,zb)为浮心坐标。
一阶项可进一步划分为
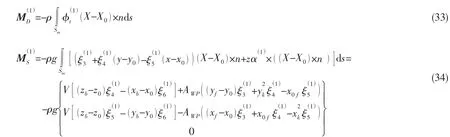
二阶项可以表达为:

2 系泊缆索/张力腿/立管动力分析方法
对于系泊缆索/张力腿/立管的静动力分析,基于Garrett提出的细长杆动力学理论,利用有限元方法建立相应的数值模型,采用Newmark法和N-R迭代法联合求解缆索的动力响应。
在此理论中,细长杆的形态按照其中心线的位置进行描述。在变形构形中,杆的中心线由空间曲线r(s,t)表示。位置向量r是弧长s和时间t的函数。假定作用在系泊缆索/张力腿/立管上的扭矩和外部力矩均为0,我们可以得到一个关于位置向量r(s,t)的线性动量守恒方程:

式中:右上标符号“′”代表对弧长s求导数,向量r上方的点“·”表示对时间求导;B=EI为弯曲刚度;T为局部张力;κ为局部曲率;ρ为单位长度质量;q为作用在单位长度杆上的分布外力。标量函数λ也称为拉格朗日乘子。如果认为杆件是可以伸长的,并且伸长量是线性小量,则线弹性伸长条件为

其中:At=Ae-Ai,Ae和Ai分别为外部和内部横截面积。这些方程充分考虑了几何非线性的影响,并且没有对缆索的形状和方向做具体假定。本理论模型的优点在于:公式(40)直接在一个总体坐标系中进行定义,而且不需要与局部坐标系进行任何坐标变换。
作用在杆件上的外力主要来自周围环境流体的静水压力和水动态荷载,以及杆件自身的重力。因此,外力q可以表达为

式中:w为杆件在空气中单位长度所受重力,Fs和Fd分别为单位长度上的静水压力和水动力荷载,并且可以分别表达为:
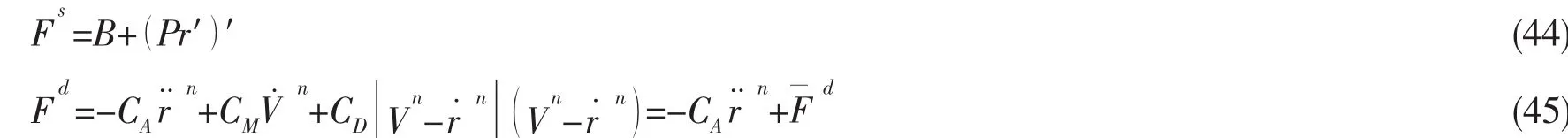
其中:B为单位长度上的浮力,并且假定横截面受到静水压力的作用。标量P为杆件上任意点r处的静水压力,定义为P=PeAe-PiAi,Pe和Pi分别为外部静水压力和内部流体产生的压力。Fd是根据莫里森方程进行计算的,式中的CA为单位长度附加质量,CM为单位长度单位法向加速度所受惯性力,CD为单位长度单位法向速度所受拖曳力。Vn和V˙n分别为垂直于杆件中心线的法向流体速度和加速度。
最终,杆件在自重、静水压力和水动力荷载作用下的运动方程可以表达为

建立了有限元模型求解上述系泊动力问题,此数值方法的详细描述可参见Ran(2000)。该有限元程序适用于比例极限范围内具有小变形的任意材料组合柔性结构。总体切线刚度矩阵和残余力向量可以由相应的单元矩阵和向量进行组装得到,最后可以形成系泊缆索/张力腿/立管的增量平衡方程进行求解。
3 耦合动态分析方法
通过导缆孔处边界条件的匹配,将系泊动力分析程序和浮式平台的动力分析程序进行耦合。浮式平台的一阶和二阶耦合运动方程可以表达为:
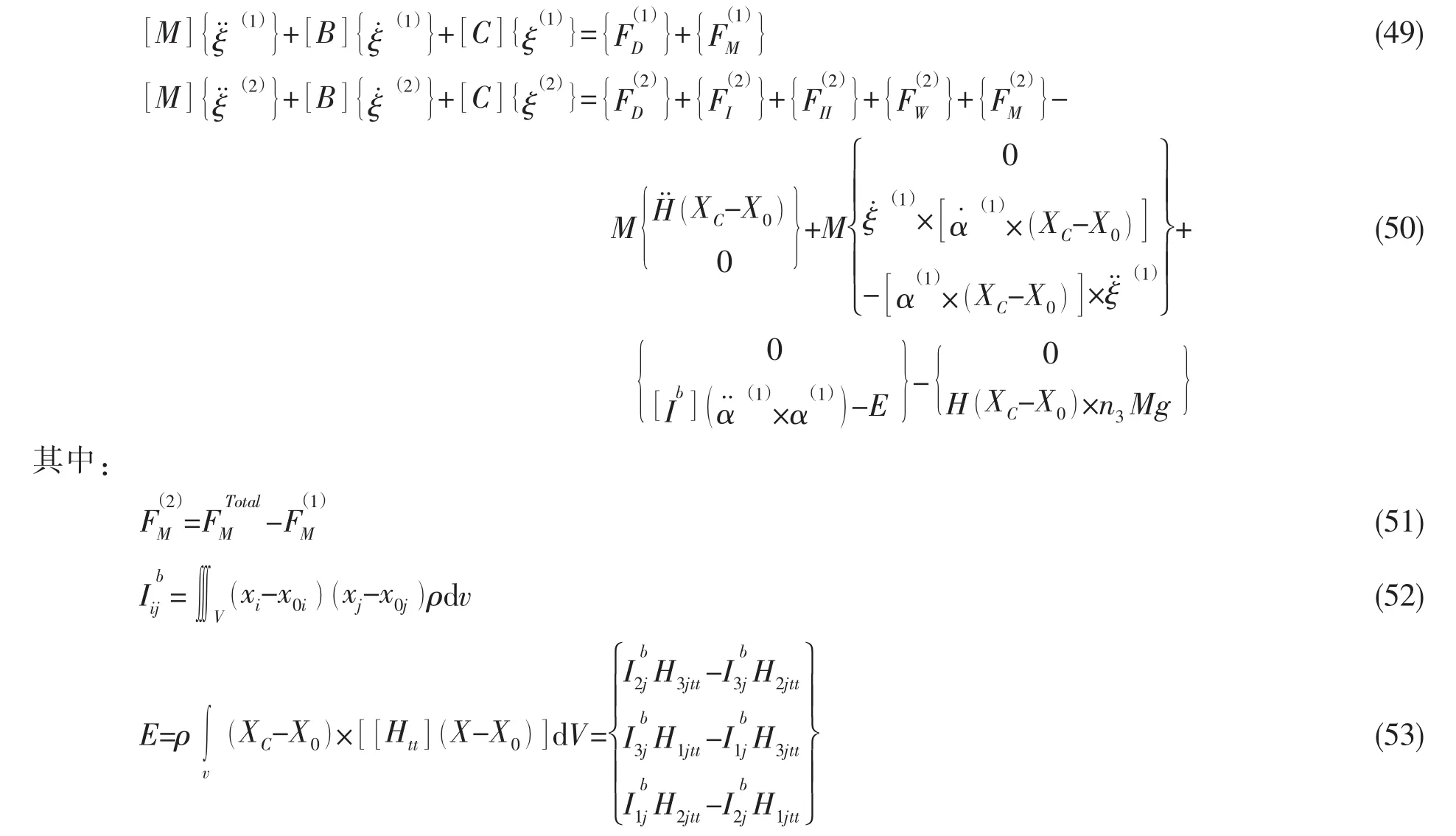
在数值求解过程中,利用四阶预报校正方法更新波面和自由水面上的速度势,将Newmark-β法和N-R迭代法进行结合,同时求解浮式平台和系泊缆索/张力腿/立管的运动方程。为了简便起见,可以将浮式平台的运动方程重新表达为一般形式:

如果K代表时间步,t=KΔt,则在时间步K时浮式平台和缆索的运动方程可以分别表达为:

方程(56)中质量矩阵、刚度矩阵和力向量与Tahar和Kim[9]文章中的表达式相似。
4 桁架式Spar 平台与系泊/立管系统的耦合动态分析
在本数值算例中,主要考察规则波作用下桁架式Spar平台与其系泊/立管系统的耦合运动响应,并将平台运动的时域耦合分析结果与频域QTF结果进行了比较。图2为Spar平台的侧视图,图3为平台的基本尺寸示意图,平台的主要特性数据如表1所示。所模拟的规则入射波波幅为A=6.0 m,波浪周期为T=10.0 s,波浪入射角度为0度。在数值模拟中忽略了桁架结构、月池和浮舱的影响。利用桁架式Spar平台的对称性,在1/4物面和自由水面上剖分网格,图4为Spar平台的网格划分示意图。
Truss Spar平台采用对应实际水深1 500 m的12点系泊系统,由3组、每组4根共12根相同的组合系泊缆索构成,每组间隔120°,每组中的系泊缆索间隔5°。总体动力性能分析所采用系泊系统的配置及其坐标系统如图5所示,组合系泊缆索为链—缆—链复合型式,自上(导缆孔)而下(海底锚)分别由船链、钢缆和底链3段组成,表2为组合系泊缆的主要物理属性,系泊系统的系泊点及其预张力配置如表3所示。

图2 Spar平台侧视图Fig.2 Spar outboard profile(Looking west)

图3 平台主要尺寸示意图Fig.3 Main dimensions of the Truss Spar

表1 平台主要特性数据Tab.1 Main particulars of the Truss Spar

图4 Truss Spar平台物面和自由水面网格剖分模型Fig.4 Mesh grid model on the body-surface and free-surface for the Truss Spar

图5 系泊系统配置及坐标系统Fig.5 Mooring configuration and coordinate system

表2 组合系泊缆主要物理属性Tab.2 Main properties of the combined mooring line

续表2

表3 系泊系统导缆孔位置及预张力配置Tab.3 Fairlead location and pretension summary of the mooring system
平台配备有6根生产立管和1根钻井立管。生产立管的张力由独立于平台主体的浮力罐支撑,钻井立管的张力由平台上的张紧器支撑。立管的物理属性及其预张力设置如表4所示。
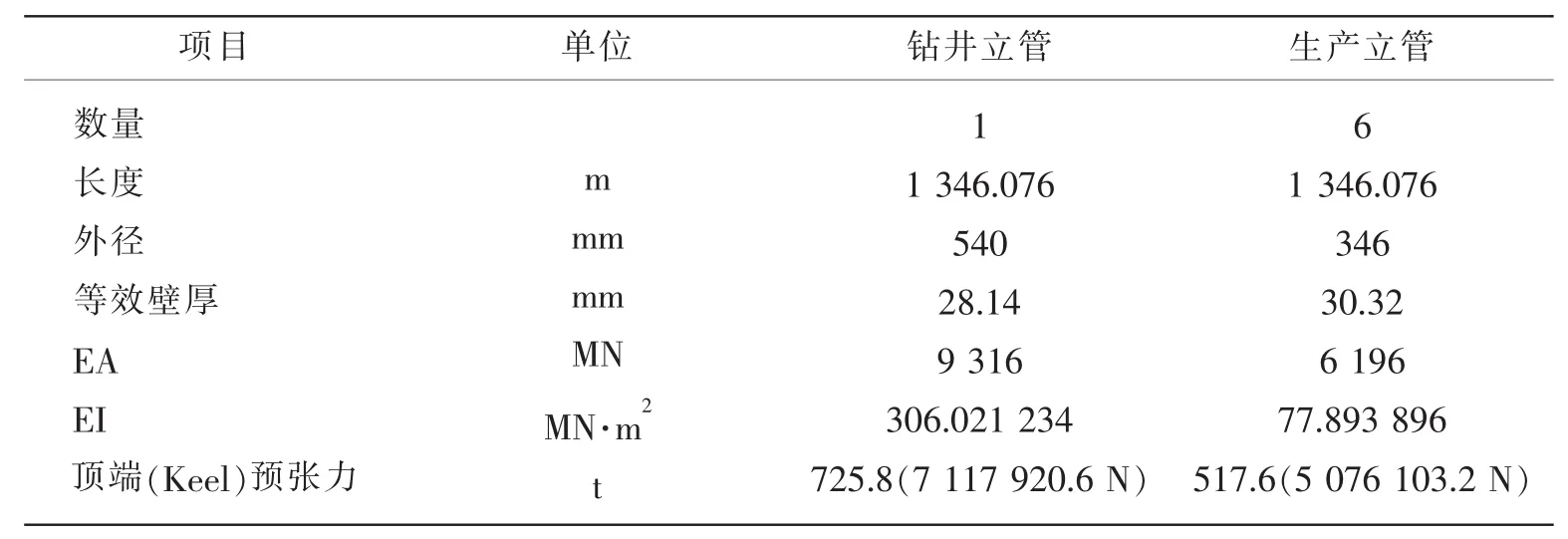
表4 立管主要参数Tab.4 Main parameters of the risers
对规则波作用下桁架式Spar平台的运动响应进行了研究,全部响应结果均是相对于平台重心。同时给出了QTF频域计算的运动响应,与本文全时域耦合分析模型的计算结果进行了对比。在平台的初始静平衡位置,采用数值方法计算系泊/立管系统的恢复力矩阵,然后利用此线性化的系泊恢复刚度在频域中计算平台的位移。图6-8分别给出了平台的纵荡、升沉和纵摇响应,它们的变化趋势基本一致,从运动响应的对比结果可以看出,QTF结果和本文全时域准静态耦合分析(COUPLE_QS)的结果更加一致,这是因为频域方法同样忽略了系泊系统的动力效应,同时也说明了本文建立的全时域耦合模型的正确性。可以发现,动态耦合分析(COUPLE_DY)和准静态耦合分析不仅在响应幅值上有明显不同,在自振频率下瞬态响应的衰减速度上也有所不同。从图6(b)可以看出,由于系泊阻尼及系泊/立管系统动力效应的影响,COUPLE_DY的二阶纵荡达到的最大值比COUPLE_QS要小,自振频率下的瞬态响应比COUPLE_QS衰减更快。由于二阶平均漂移力的存在,可以看到平台发生了一个较大的平均偏移。与纵荡和纵摇相比,系泊系统动态力对一阶升沉的影响较大,而且二阶升沉对总升沉的贡献也较大。总体而言,倍频响应相对较小,对于规则波,波频响应和自振频率下的瞬变响应占据主导地位。COUPLE_QS计算结果与QTF结果有较好的一致性,但是由于动力耦合效应的影响,与COUPLE_DY计算结果存在一定差别。从耦合响应与频域结构的比较可以发现,本文建立的全时域耦合分析模型可以很好地预报浮式平台的运动。
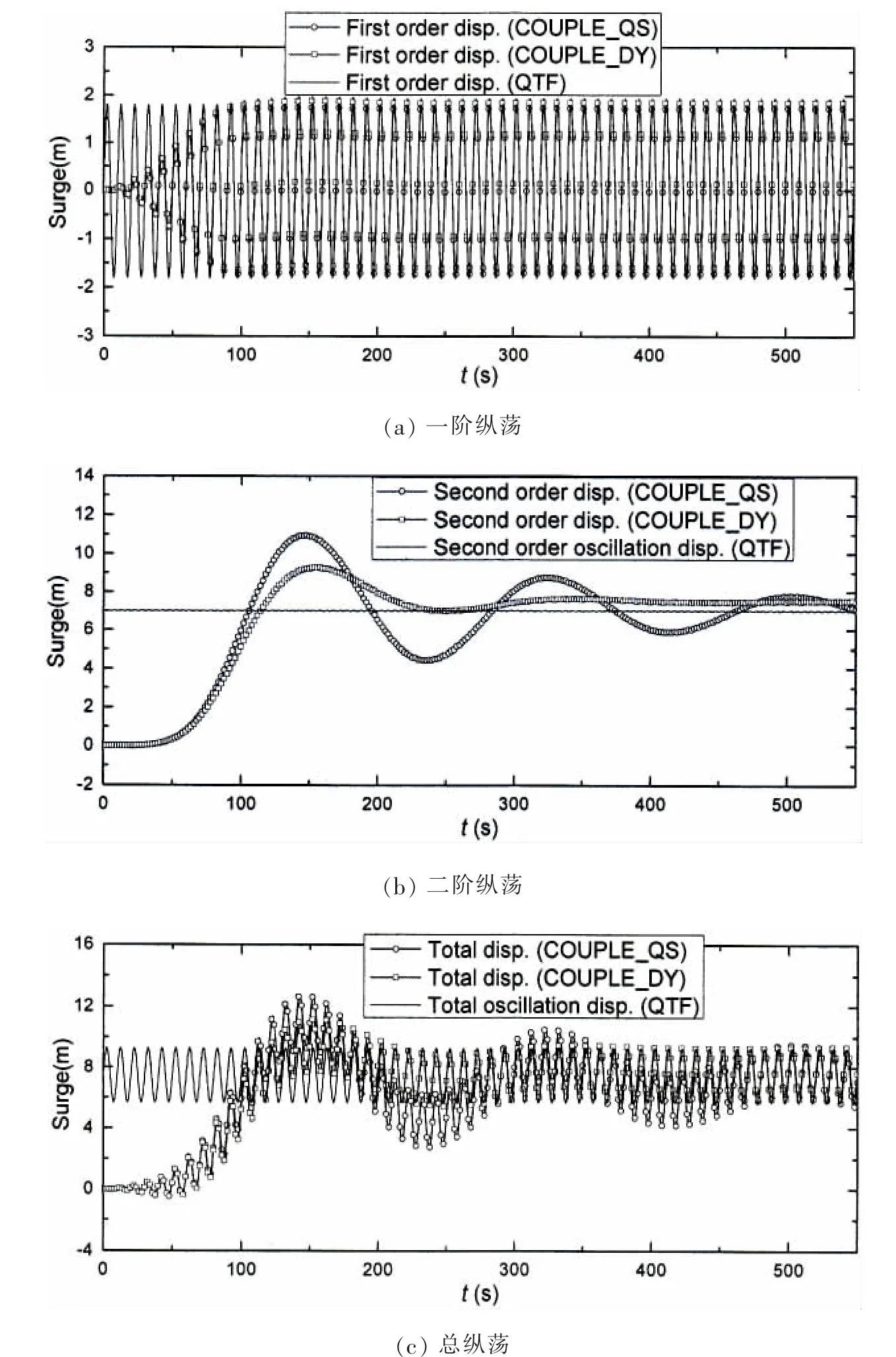
图6 规则波作用下Truss Spar的纵荡响应Fig.6 Surge response of the Truss Spar in regular waves

图9 2号系泊缆索上端点张力Fig.9 The top node tensions of mooring line 2
本文同时还给出了系泊缆索/立管上端点张力和水线上两个特征点处的波面升高。图9为2号缆索上端点张力模拟结果,一阶张力和总张力的时间历程分别如图9(a)和图9(b)所示。从图中可以看出,COUPLE_DY计算的系泊张力比COUPLE_QS要大很多,这说明系泊缆索惯性力和拖曳力对系泊张力的影响较大,而且张力的变化趋势与纵荡响应类似。

图10 生产立管上端点的一阶张力Fig.10 The first order top node tensions of production riser

图11 生产立管上端点的总张力Fig.11 The total top node tensions of production riser
图10为生产立管上端点的一阶张力,图11为上端点总张力。从两幅图中可以看出,作用在立管上的动态力的影响也非常大,动态耦合方法比准静态耦合方法计算的张力幅值更大,总张力的大小和变化幅度比一阶张力大。但是对于立管而言,由于上端点施加的边界条件的原因,立管上端点张力的变化范围较小,基本保持在预张力附近波动。
图12和图13分别为水线上θ=0和θ=π两点的波面升高,θ是与x轴正方向的夹角。可以看出,两种耦合分析方法得到的波面升高时间历程几乎相同,迎浪侧的波浪爬高明显大于背浪侧,总波浪爬高大于一阶波浪爬高。


图13 迎浪侧水线上θ=π点的波面升高Fig.13 The wave elevation at the water-line point on wave-side(θ=π)
5 结 语
本文建立了一个新的全时域非线性耦合动态分析模型。在此模型中,直接在时域内计算非线性波浪力,而非采用传统频时变换的间接方法,同时建立了基于细长杆理论的有限元方法对系泊缆索/立管进行动力分析。通过在导缆孔处施加恰当的边界条件,将浮式平台的运动方程和系泊/立管系统的动力方程整体进行耦合。在每个时间步,利用Newmark-β法和N-R迭代法,对平台运动方程和系泊缆索/立管动力方程同时进行求解。
利用建立的耦合分析模型对一个桁架式Spar平台及其系泊/立管系统进行了数值模拟,分别采用动态耦合方法(COUPLE_DY)和准静态耦合方法(COUPLE_QS)进行了分析,为了进行对比研究,同时给出了采用QTF方法计算的频域结果。由于存在二阶平均漂移力,Spar平台发生了较大的平均偏移。从耦合分析结果中可以发现,在深水中尤其是在平台做大幅运动响应时,浮式平台和系泊/立管系统之间的动力耦合效应起着非常重要的作用,系泊缆索惯性力和阻尼力对深水顺应式平台的动力分析有重要影响。利用本文建立的耦合分析模型,可以对平台的波频和低频响应进行可靠预报。
[1]Ma W,Lee M Y,Zou J,Huang E.Deepwater nonlinear coupled analysis tool[C]//In:Proceedings of the Offshore Technology Conference,OTC 12085.Houston,Texas,2000.
[2]Lee M Y,Flory J.ABS guide for synthetic ropes in offshore mooring applications[C]//In:Proc.Offshore Technology Conference,OTC 10910.Houston,Texas,1999.
[3]Lee M Y,Devlin P.Development of API RP 2SM for synthetic fiber rope moorings[C]//Proc.Offshore Technology Conference,OTC 12178.Houston,Texas,2000.
[4]Kim M H,Tahar A,Kim Y B.Variability of Spar motion analysis against various design methodologies/parameters[C]//In: Proceedings of the Twentieth Offshore Mechanics and Artic Engineering Conference,OMAE01-OFT1063.Rio de Janeiro, Brazil,2001a.
[5]Kim M H,Tahar A,Kim Y B.Variability of TLP motion analysis against various design methodologies/parameters[C]//In: Proceedings of the International Offshore and Polar Engineering Conference,ISOPE 3.Stavanger,Norway,2001b.
[6]Ran Z.Coupled dynamic analysis of floating structures in waves and current[D].Ph.D dissertation,Texas A and M University,2000.
[7]Garrett D L.Coupled analysis of floating production systems[J].Ocean Engineering,2005,32:802-816.
[8]Kim M H,Koo B J,Mercier R M,Ward E G.Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment[J].Ocean Engineering,2005,32:1780-1802.
[9]Tahar A,Kim M H.Coupled-dynamic analysis of floating structures with polyester mooring lines[J].Ocean Engineering, 2008,35:1676-1685.
[10]Low Y M,Langley R S.A hybrid time/frequency domain approach for efficient coupled analysis of vessel/mooring/riser dynamics[J].Ocean Engineering,2008,35(5-6):433-446.
[11]Chen X,Ding Y,Zhang J,Liagre P,Niedzwecki J,Teigen P.Coupled dynamic analysis of a mini TLP:Comparison with measurements[J].Ocean Engineering,2006,33(1):93-117.
[12]Zhang F,Yang J,Li R,Chen G.Coupling effects for cell-truss Spar platform:Comparison of frequency-and time-domain analyses with model tests[J].Journal of Hydrodynamics,2008,20(4):424-432.
[13]de Kat J O,Dercksen A.The influence of wave spectrum formulation on the dynamics of a turret-moored tanker[J].Journal of Offshore Mechanics and Arctic Engineering,1994,116:7-13.
[14]Ran Z,Kim M H.Nonlinear coupled responses of a tethered Spar platform in waves[J].International Journal of Offshore and Polar Engineering,1997,7(2):111-118.
[15]Ormberg H,Larsen K.Coupled analysis of floating motion and mooring dynamics for a turret moored tanker[J].BOSS, 1997,2:469-483.
[16]Ran Z,Kim M H,Zheng W.Coupled dynamic analysis of a moored Spar in random waves and currents(time-domain vs frequency-domain analysis)[C].In:Proceedings of the 17th OMAE Conference,OMAE-0604,1998.
[17]Ormberg H,Sodahl N,Steinkjer O.Efficient analysis of mooring systems using de-couple and coupled analysis[C].In: Proceedings of the 17th OMAE Conference,OMAE-0351,1998.
[18]Tahar A,Halkyard J,Irani M.Comparison of time and frequency domain analysis with full scale data for the horn mountain Spar during Hurricane Isidore[C]//In:Proceedings of the Twenty fifth Offshore Mechanics and Artic Engineering Conference.Hamburg,Germany,2006.
[19]Yang C K,Kim M H.Transient effect of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis [J].Ocean Engineering,2010,37:667-677.
[20]Teng B,Yang M.Nonlinear coupled dynamic analysis for waves and a moored platform in time domain[C]//The 26th International Workshop on Water Waves and Floating Bodies.Athens,Greece,2011.
[21]Isaacson M,Ng J Y T.Second-order wave radiation of three-dimensional bodies by time-domain method[J].Int.J Offshore of Polar Eng.,1993,3(4):264-272.
[22]Garrett D L.Dynamic analysis of slender rods[J].Journal of Energy Resources Technology,Transactions of ASME,1982, 104:302-307.
[23]Kim C H,Kim M H,Liu Y H,Zhao C T.Time domain simulation of nonlinear response of a coupled tlp system[J].Int.J Offshore of Polar Eng.,1994,4(4):284-291.
Full time-domain nonlinear coupled dynamic analysis of Truss Spar and mooring/riser system
YANG Min-dong1,2,TENG Bin3,NING De-zhi3,SHI Zhong-min4
(1.Guangdong Electric Power Design Institute Co.,Ltd.of China Energy Engineering Group,Guangzhou 510663,China; 2.Department of Ocean Engineering,Ocean University of China,Qingdao 266100,China;3.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China;4.Research Center of CNOOC,Beijing 100027,China)
A full time-domain program is developed for the coupled dynamic analysis of floating platform systems.For the hydrodynamic loads,a time domain second order method is developed.In this approach, Taylor series expansions are applied to the body surface and free-surface boundary conditions,and Stokes perturbation procedure is used to establish corresponding first-order and second-order boundary value problems with time-independent boundaries.A higher-order boundary element method(HOBEM)is developed to calculate the velocity potential of the resulting flow field at each time step.The free-surface boundary condition is satisfied to the second order by 4th order Adams-Bashforth-Moultn method.An artificialdamping layer is adopted on the free surface to avoid the wave reflection.The mooring-line/tendon/riser dynamics are based on a rod theory and finite element method(FEM),with the governing equations described in a global coordinate system.In the coupled dynamic analysis,the motion equation for the hull and dynamic equations for mooring-lines/tendons/risers are solved simultaneously using Newmark method.The coupled analysis program is applied for a Truss Spar motion response simulation.Numerical results including hull motions and tensions at the top of mooring-lines/risers are presented,and some significant conclusions are derived.
full time-domain;Truss Spar;mooring-line;finite element;coupled dynamic analysis
P75
A
10.3969/j.issn.1007-7294.2015.07.007
1007-7294(2015)07-0810-17
2014-12-18
国家自然科学基金资助项目(11072052);国家重点基础研究发展计划(973)资助项目(2011CB013703)
杨敏冬(1982-),男,博士,高级工程师,E-mail:yangdongmin@gedi.com.cn;
滕 斌 (1958-),男,教授,博士生导师。
